Решение испытание на растяжение
Испытание на растяжение металла заключаются в растяжении образца с построением графика зависимости удлинения образца (Δl) от прилагаемой нагрузки (P), с последующим перестроением этой диаграммы в диаграмму условных напряжений (σ — ε)
Испытания на растяжение проводятся по ГОСТ 1497, по этому же ГОСТу определяются и образцы на которых проводятся испытания.
 Как уже говорилось выше, при испытаниях строится диаграмма растяжения металла. На ней есть несколько характерных участков:
Как уже говорилось выше, при испытаниях строится диаграмма растяжения металла. На ней есть несколько характерных участков:
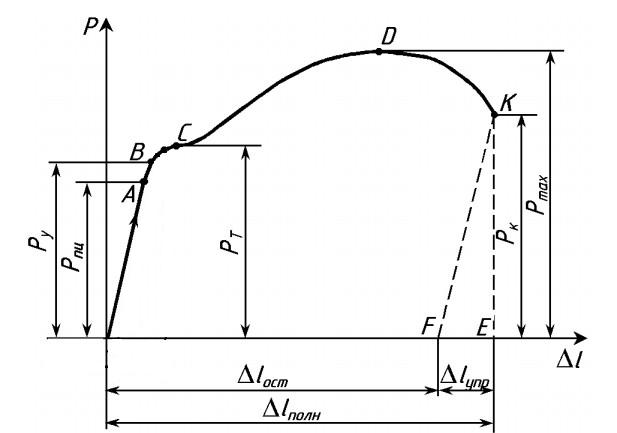
- Участок ОА — участок пропорциональности между нагрузкой Р и удлинением ∆l. Это участок, на котором сохраняется закон Гука. Данная пропорциональность была открыта Робертом Гуком в 1670 г. и в дальнейшем получила название закона Гука.
- Участок ОВ — участок упругой деформации. Т.е., если к образцу приложить нагрузку, не превышающую Ру, а потом разгрузить, то при разгрузке деформации образца будут уменьшаться по тому же закону, по которому они увеличивались при нагружении
Выше точки В диаграмма растяжения отходит от прямой — деформация начинает расти быстрее нагрузки, и диаграмма принимает криволинейный вид. При нагрузке, соответствующей Рт (точка С ), диаграмма переходит в горизонтальный участок. В этой стадии образец получает значительное остаточное удлинение практически без увеличения нагрузки. Получение такого участка на диаграмме растяжения объясняется свойством материала деформироваться при постоянной нагрузке. Это свойство называется текучестью материала, а участок диаграммы растяжения, параллельный оси абсцисс, называется площадкой текучести.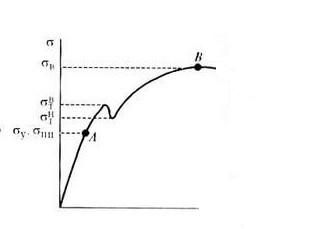 Иногда площадка текучести носит волнообразный характер. Это чаще касается растяжения пластичных материалов и объясняется тем, что вначале образуется местное утонение сечения, затем это утонение переходит на соседний объем материала и этот процесс развивается до тех пор, пока в результате распространения такой волны не возникает общее равномерное удлинение, отвечающее площадке текучести. Когда имеется зуб текучести, при определении механических свойств материала, вводят понятия о верхнем и нижнем пределах текучести.
Иногда площадка текучести носит волнообразный характер. Это чаще касается растяжения пластичных материалов и объясняется тем, что вначале образуется местное утонение сечения, затем это утонение переходит на соседний объем материала и этот процесс развивается до тех пор, пока в результате распространения такой волны не возникает общее равномерное удлинение, отвечающее площадке текучести. Когда имеется зуб текучести, при определении механических свойств материала, вводят понятия о верхнем и нижнем пределах текучести.
После появления площадки текучести, материал снова приобретает способность сопротивляться растяжению и диаграмма поднимается вверх. В точке D усилие достигает максимального значения Pmax. При достижении усилия Pmax на образце появляется резкое местное сужение — шейка. Уменьшение площади сечения шейки вызывает падение нагрузки и в момент, соответствующий точке K диаграммы, происходит разрыв образца.
Прилагаемая нагрузка для растяжения образца зависит от геометрии этого образца. Чем больше площадь сечения, тем более высокая нагрузка необходима для растяжения образца. По этой причине, получаемая машинная диаграмма не дает качественной оценки механических свойств материала. Чтобы исключить влияние геометрии образца, машинную диаграмму перестраивают в координатах σ − ε путем деления ординат P на первоначальную площадь сечения образца A0 и абсцисс ∆l на lо. Перестроенная таким образом диаграмма называется диаграммой условных напряжений. Уже по этой, новой диаграмме, определяют механические характеристики материала.
Определяются следующие механические характеристики:
Предел пропорциональности σпц – наибольшее напряжение, после которого нарушается справедливость закона Гука σ = Еε , где Е – модуль продольной упругости, или модуль упругости первого рода. При этом Е =σ/ε = tgα , т. е. модуль E это тангенс угла наклона прямолинейной части диаграммы к оси абсцисс
Предел упругости σу — условное напряжение, соответствующее появлению остаточных деформаций определенной заданной величины (0,05; 0,001; 0,003; 0,005%); допуск на остаточную деформацию указывается в индексе при σу
Предел текучести σт – напряжение, при котором происходит увеличение деформации без заметного увеличения растягивающей нагрузки
Также выделяют условный предел текучести — это условное напряжение, при котором остаточная деформация достигает определенной величины (обычно 0,2% от рабочей длины образца; тогда условный предел текучести обозначают как σ0,2). Величину σ0,2 определяют, как правило, для материалов, у которых на диаграмме отсутствует площадка или зуб текучести
Предел прочности (временное сопротивление разрыву) σв – напряжение, соответствующее наибольшей нагрузке Pmax , предшествующей разрыву образца
Кроме характеристик прочности материала, при испытании на растяжение определяют также характеристики пластичности — относительное удлинение δ и относительное сужение ψ
где lо – первоначальная расчетная длина образца, а lк – конечная расчетная длина образца

Изопропиловый спирт цена за тонну оптом — https://www.dcpt.ru
Источник
Механические характеристики материала определяются в результате испытания образца на специальных прессах. Форма образца может быть различной, но чаще всего стержень с участком постоянного поперечного сечения (круглого или прямоугольного) длиной . Концы образца имеют специальные утолщения для их закрепления в испытательной машине.
Перед началом испытания материала на растяжение замеряется площадь поперечного сечения () средней части образца. Значение растягивающей силы (P) и удлинения его средней части () в каждый момент нагружения определяются специальными устройствами. При испытании нагрузка увеличивается медленно и плавно.
Современные испытательные машины снабжены записывающим прибором, который при испытании образца автоматически вычерчивает график зависимости между нагрузкой (P) и абсолютным удлинением (). График называется диаграммой растяжения (или диаграмма Бернулли).
Рассмотрим диаграмму растяжения для стали марки Ст. 3 (рис. 2.3). Эта диаграмма характеризует поведение данного образца, но не материала, из которого он сделан.
В начальной стадии испытания, до точки А с ординатой , зависимость между силой (P) и удлинением () носит линейный характер, что свидетельствует о линейной деформируемости образца. Затем диаграмма искривляется и при некотором значении растягивающей силы наблюдается значительный рост удлинения образца без увеличения нагрузки (текучесть материала). Практически горизонтальный участок диаграммы BC называется площадкой текучести, а точка B – критической точкой диаграммы.
При некотором значении растягивающей силы , соответствующем критической точке B (см. рис. 2.3), на поверхности образца, если он, например, полирован, заметно появление сначала нескольких полосок, параллельных между собой и расположенных под углом примерно к оси образца. Далее появляется вторая система линий, пересекающая первую и наклоненную к оси под тем же углом, что и первая. Такая система сопряженных линий называется линиями Людерса – Чернова, представляющие собой следы сдвигов частиц материала. Направления линий Людерса-Чернова соответствует площадкам, на которых при растяжении возникают наибольшие касательные напряжения.
За точкой C диаграммы удлинение образца начинает расти быстрее нагрузки. Число линий Людерса – Чернова растет, они сливаются друг с другом и, наконец, теряют ясность своих очертаний. Этот участок диаграммы растяжения называется зоной упрочнения.
В наивысшей точке диаграммы D при силе равной на образце внезапно появляется местное сужение – шейка, которая представляет собой результат накопления деформаций сдвига.
Сопротивление образца растяжению, после образования шейки, падает и его разрыв происходит в точке K при нагрузке:
.
При разрыве образца, как правило, появляется поперечная трещина в центре тяжести поперечного сечения (посредине шейки), а остальная часть сечения скалывается под углом к оси образца так, что на одной части разорванного образца образуется выступ, а на другой – кратер.
Линия разгрузки образца KL оказывается прямой и параллельной начальному участку диаграммы ОА. Следовательно, полная деформация образца состоит из двух частей: упругой, исчезающей после снятия нагрузки, и остаточной (пластической).
Источник
1. ВВЕДЕНИЕ
В методических указаниях к лабораторной работе № 1 «Испытание на растяжение образца из конструкционной стали» указывается цель работы, приводится характеристика испытуемого образца и дается методика проведения испытаний.
Для лучшего усвоения материала по теме растяжения и сжатия приводятся основные теоретические положения, позволяющие квалифицированно провести обработку полученной диаграммы Р-Δl и вычислить механические характеристики материала испытуемого образца. Даны также рекомендации как провести анализ полученных результатов и сделать правильные выводы по выполненной лабораторной работе.
Завершаются методические указания перечнем возможных вопросов при защите отчета по этой лабораторной работе. А в качестве предисловия перед описанием первой лабораторной работы приводятся рекомендации к оформлению отчета по лабораторным работам.
2. РЕКОМЕНДАЦИИ К ОФОРМЛЕНИЮ ОТЧЕТА ПО ЛАБОРАТОРНЫМ РАБОТАМ
По каждой выполненной работе студентом оформляется отчет. В содержании отчета отражаются следующие основные моменты:
- название лабораторной работы,
- цель лабораторной работы,
3) оборудование, приборы и инструменты, используемые при проведении лабораторной работы,
4) характеристика образцов до испытания (форма и геометрические размеры, материал),
- краткие сведения из теории по теме выполняемой работы,
- порядок проведения испытаний,
- результаты испытаний (журнал наблюдений, характеристика образцов после испытаний и т.п.),
- обработка результатов испытаний и их анализ,
- выводы по выполненной лабораторной работе.
Для оформления отчета по лабораторным работам можно использовать отдельную тетрадь или листы форматом 210 χ 297 мм, сброшюрованные в общепринятой форме. В конце семестра отчет по лабораторным работам сдается преподавателю.
3. ЦЕЛЬ РАБОТЫ
Получить диаграмму растяжения, вычислить механические характеристики конструкционной стали при растяжении и по ним определить марку конструкционной стали испытуемого образца.
4. ОБОРУДОВАНИЕ, ПРИБОРЫ И ИНСТРУМЕНТЫ
Испытательная машина – УММ-5. Штангенциркуль.
5. ХАРАКТЕРИСТИКА ОБРАЗЦА
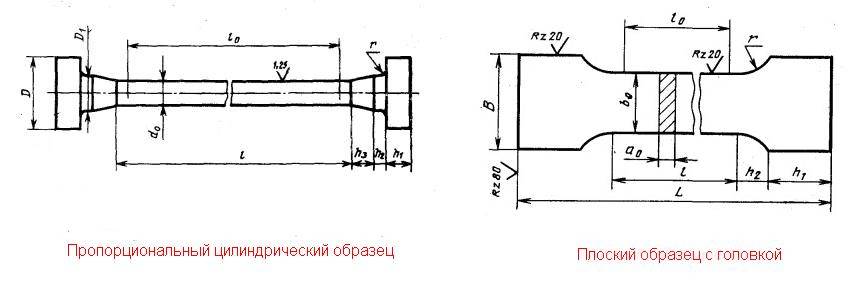
Для испытания на растяжение используются специально изготовленные образцы, которые вытачиваются из прутка или вырезаются из листа. Основной особенностью этих образцов является наличие длинной, сравнительно тонкой рабочей части и усиленных мест (головок) по концам для захвата.
Для получения сравнимых результатов испытаний образцы с цилиндрической или прямоугольной формой поперечного сечения рабочей части изготавливаются по ГОСТ 1497-84. Проводятся испытания цилиндрического образца, форма и размеры которого приведены на рис. 1.
Рис.1. Цилиндрический образец: I 0 – расчетная длина образца = ΙΟ*d ,
l1 – рабочая длина образца = 12,5·
,
l 2 – длина конусообразной части образца = 10
-1 0 / 2 ,
l3 – длина головки образца = d ,
L – полная длина образца ,
d – диаметр сечения расчетной и рабочей длины =1,13·
,
d1 – диаметр основания конуса (у головки ) = 1,5·
d2 – диаметр головки образца = 2·
Для замера деформаций на расчетной части образца отмечают отрезок, называемый расчетной длиной.
Чаще всего применяются цилиндрические образцы, у которых расчетная длина равна десяти диаметрам (длинные образцы) и образцы с расчетной длиной равной пяти диаметрам (короткие образцы). Чтобы результаты испытаний образцов прямоугольного и круглого сечений были сопоставимы,
в случае прямоугольного сечения в качестве характеристики, определяющей расчетную длину, принимается диаметр равновеликого круга.
6. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Основным и наиболее распространенным является испытание на растяжение, при котором удается получить наиболее важные характеристики материала, находящие прямое применение в расчетной практике.
При растяжении образца изучают зависимость между действующей нагрузкой и соответствующим удлинением. Графическое изображение этой зависимости называют диаграммой растяжения. Типичная для конструкционных сталей диаграмма растяжения показана на рис.2.
Ρ
О F Ε
Рис.2. Типичная диаграмма растяжения конструкционных сталей
По оси ординат отложены усилия Ρ в масштабе сил, а по оси абсцисс – удлинение образца Δl в масштабе удлинений. Полученная кривая условно может быть разделена на четыре участка.
Участок ОА – прямолинейный, носит название зоны упругости, здесь материал подчиняется закону Гука:
l=Pl/EF
Участок АВ называется зоной текучести, а горизонтальный отрезок этого участка – площадкой текучести. Здесь происходит существенное изменение длины образца без заметного увеличения нагрузки. Наличие площадки текучести для материалов не является обязательным. Во многих случаях при испытаниях на растяжение площадки текучести нет. Такое типично для алюминия, отожженной меди, для высококачественных легированных сталей и других материалов.
Участок ВС называется зоной упрочнения. Здесь удлинение образца сопровождается возрастанием нагрузки, но значительно более медленно (в сотни раз), чем на упругом участке.
Если в произвольной точке К зоны упрочнения ВС (рис. За.), образец разгрузить, то в процессе разгрузки зависимость между силой Ρ и удлинением
l изобразится прямой KL. Как показывает опыт, эта прямая параллельна прямой ОА. Таким образом, при разгрузке деформация полностью не исчезает. Она лишь уменьшается на величину упругой части (отрезок LM). Отрезок OL представляет собой остаточное или пластическое удлинение. Таким образом, полная деформация (отрезок ОМ) состоит из упругой и остаточной (пластической) частей, т.е. Δl = Δl упр+ Δ/ ост.
Если образец был нагружен в пределах участка ОА, а затем разгружен, то удлинение будет чисто упругим (Δ I ост = 0 ) и образец вернется в исходное состояние. Таким образом при повторном нагружении образца диаграмма растяжения идет по прямой LК и возвращается на кривую KCD так, как будто промежуточной разгрузки не было.
Предположим, что у нас имеется два одинаковых образца, изготовленных из одного и того же материала. Один из образцов до испытания нагружению не подвергался, другой образец был нагружен до точки К, а после разгрузки снят с машины. Испытывая первый образец, мы получим обычную диаграмму растяжения OABCD, показанную на рис.За. При испытании второго образца отсчет удлинения будет производиться, естественно, от ненагруженного состояния и остаточное удлинение OL учтено не будет (при нагружении диаграмма пойдет по прямой LK). В результате получим укороченную диаграмму (рис.36.). Отрезок МК соответствует силе предварительного нагружения. Таким образом, вид диаграммы растяжения для одного и того же материала зависит от степени предварительного нагружения. Очень важно, что отрезок LK больше отрезка ОА.
D
Μ
F Ε
L M PEL
Рис.3. Диаграммы растяжения ‘
а – полная для предварительно незагруженного образца,
б – укороченная для предварительно загруженного до т.К образца
Следовательно, в результате предварительного нагружения. материал приобретает способность воспринимать без остаточных удлинений большие нагрузки. Это явление называется наклепом и широко используется в технике.
В конце зоны упрочнения на образце намечается место будущего разрыва и начинается образование так называемой шейки -местное сужение образца ( рис.4.).
Рис.4. Местное сужение образца – шейка
Деформации до этого распределяются равномерно по всему образцу. С момента начала образования шейки, деформации преоб-ретают местный характер, концентрируясь около какого – то сечения, оказавшегося самым слабым в силу случайных факторов -здесь и образуется шейка. По мере растяжения образца уменьшение площади сечения шейки прогрессирует.
Когда относительное уменьшение площади сечения шейки сравнивается с относительным возрастанием напряжения, сила Ρ достигает максимума (точка С). В дальнейшем удлинение образца происходит с уменьшением силы, хотя среднее напряжение в поперечном сечении шейки и возрастает. Удлинение образца носит в этом случае местный характер и поэтому участок CD называется зоной местной текучести. Точка D соответствует разрушению образца. У многих материалов разрушение происходит без заметного образования шейки.
Диаграммы растяжения, записанные испытательной машиной в координатах (Ρ –
l), зависят не только от материала,но и от размеров образца. Удобнее пользоваться диаграммой, у которой по оси ординат откладывается усилие, деленное на первоначальную площадь сечения образца fo , а по оси абсцисс – удлинение отнесенное к расчетной длине образца I о. Величина σ=Ρ/Fο называется напряжением, а величина ε=Δl / lo относительным удлинением. Так как fо и iо постоянны, то диаграмма σ-ε ( рис.5.) имеет тот же вид, что и диаграмма растяжения в координатах (Ρ-Δl), но будет характеризовать уже не свойства образца, а свойства материала. В случае необходимости вместо диаграммы σ-ε, можно использовать диаграмму растяжения (Ρ-Δl), пересчитав предварительно масштабы.
Рис.5. Диаграмма напряжений (условная)
Отметим на диаграмме характерные точки и дадим определения соответствующих им числовых величин.
Пределом пропорциональности σπΐί= Рпц / fо называется наибольшее напряжение, до которого материал следует закону Гука σ=Ε·ε. Величина предела пропорциональности зависит от степени точности, с которой начальный участок диаграммы можно рассматривать как прямую. Степень отклонения кривой σ- ί'(ε) от прямой определяют по величине угла, который составляет касательная к диаграмме с осью σ. По закону Гука тангенс этого угла равен 1/Е . Обычно считают, что если тангенс угла между касательной к диаграмме и осью σ оказался на 50% большим, чем 1/Е, то предел пропорциональности достигнут.
Пределом упругости σу= Ру / fо называется такое предельное напряжение, до которого материал не получает остаточных деформаций. Для того, чтобы найти предел упругости, необходимо, очевидно, после каждой дополнительной нагрузки образец разгружать и смотреть, не появились ли остаточные деформации. Величина предела упругости, как и предела пропорциональности, зависит от точности, с которой производятся измерения. Обычно остаточную деформацию, соответствующую пределу упругости принимают в пределах
ОСТ = (l ч- 5) · КГ3, т.е. 0,001% – 0,005%.
Пределом текучести στ= Рт / fо называется то напряжение, при котором происходит рост деформаций без заметного увеличения нагрузки. В тех случаях, когда на диаграмме отсутствует площадка текучести, за предел текучести принимается условно величина напряжения, при котором остаточная деформация
oct= 0,002 или 0,2 % (в некоторых случаях oct = 0,5%). Условный предел текучести обозначается σο,2; σο,5 ,··· , в зависимости от принятой величины допуска на остаточную деформацию (в процентах).
Пределом прочности или временным сопротивлением называется отношение максимальной силы, которую выдерживает образец, к его первоначальной площади поперечного сечения(σΒ= ΡΒ / fo). Следует иметь в виду, что σΒ это не то напряжение, при котором разрушается образец.
Среднее напряжение в момент разрыва σρ, которое почему-то называют истинным, определяется отношением нагрузки в момент разрушения к площади поперечного сечения шейки в самом узком сечении σρ= Рраз / Fш , причем оно существенно больше предела прочности σΒ.
Предел пропорциональности апц, предел упругости ау, предел текучести στ, предел прочности σΒ и «истинное» напряжение в момент разрыва σρ – представляют собой прочностные характеристики материала. –
При испытании на растяжение определяют и характеристики пластичности материала (относительное остаточное удлинение δ и относительное остаточное сужение ψ).
Относительное остаточное удлинение – это относительное изменение длины рабочей зоны образца ; определяется по формуле:
Относительное остаточное сужение – это относительное изменение площади сечения в месте разрыва ; определяется по формуле:
Для оценки качества испытанного материала важно также определить работу, затраченную на разрыв образца. Чем большую работу необходимо затратить для разрыва образца, тем больше энергии в состоянии поглотить материал, не разрушаясь и тем лучше он будет сопротивляться ударным нагрузкам, поглощая кинетическую энергию удара.
Величина полной работы, затраченной при растяжении образца до его разрыва, графически изображается площадью диаграммы растяжения OABCDE с учетом масштабов сил и удлинений ( рис.3. ). Площадь треугольника DEF соответствует работе, израсходованной на упругую деформацию, исчезнувшую после разрыва. Работа затраченная на пластическую деформацию ( А ) графически определяется площадью диаграммы растяжения OABCDF с учетом I тех же масштабов сил и удлинений. ΐ
Удельная работа ( а ) – это отношение работы А к объему образца V, ( а = А / V ), в тоже время она равна площади OABCDF диаграммы σ-ε (рис.5.) с учетом масштабов. Удельная работа характеризует способность материала образца поглощать энергию разрыва, вязкость материала и сопротивляемость его динамическим воздействиям нагрузки.
7. ПОРЯДОК ПРОВЕДЕНИЯ ИСПЫТАНИЙ
- Перед испытанием студентам необходимо ознакомиться с устройством машины УММ-5 (первое занятие) и правилами пове- дения в лаборатории при проведении испытаний (вводный инструктаж).
- Измеряют штангенциркулем длину рабочей зоны, отмеченную на образце накерненными точками и диаметр образца в трех сечениях расчетной зоны. За расчетный диаметр принимают среднее значение по выполненным трем замерам.
Производится визуальная оценка качества поверхности обработки образца в пределах рабочей зоны.
- Наблюдают за закреплением образца в захватах машины, выполняемым лаборантом кафедры.
- Наблюдают за включением машины и процессом растяжения образца.
6. Внимательно следят за комментариями преподавателя по процессу нагружения образца.
- Фиксируют на силоизмерителе максимальную нагрузку после разрушения образца и выключения машины.
- Соединяют две части образца по поверхности его разрушения и штангенциркулем замеряют диаметр шейки и
8. Соединяют две части образца по поверхности его разрушения и штангенциркулем замеряют диаметр шейки и длину рабочей зоны’ после испытания. Вид образца сложенного по длине после разрушения приведен на рис.6.
9. Получают от лаборанта оригинал диаграммы растяжения, снимают копию в свой отчет и приступают к обработке диаграммы.
8. ОБРАБОТКА РЕЗУЛЬТАТОВ ИСПЫТАНИЯ
При испытании были определены по силоизмерителю значения нагрузок, соответствующих пределу текучести Рт и пределу прочности Рв . По диаграмме определяют значения нагрузки, соответствующей пределу пропорциональности Рпц и нагрузки в момент разрыва Рразр. Определяют первоначальную площадь поперечного сечения образца fo = π · d*d / 4 и объем рабочей части V = fo-I о · Площадь поперечного сечения шейки определяется по формуле Рш = π · dш*dш / 4.
Затем определяют прочностные характеристики материала образца путем деления соответствующих нагрузок на первоначальную площадь поперечного сечения образца fo :
а) предел пропорциональности σΠΙ1= Рпц / f0,
б) предел текучести στ = Рт / f0,
в) предел прочности σΒ = Рв / f0,
Так называемое «истинное» напряжение в момент разрыва определяется путем деления нагрузки в момент разрыва гра3р на площадь поперечного сечения шейки Рш , (σр=Рра/Рш).
Зная длину образца до и после испытания, находим остаточное удлинение образца Δl o=l1-l о , которое должно совпасть с отрезком OF на диаграмме, умноженном на масштаб. Разделив остаточное удлинение образца на первоначальную длину рабочей части его и умножив на 100% найдем одну из важнейших характеристик пластичности материала δ=(Δl0/lο)·100% – относительное остаточное удлинение.
Другой характеристикой пластичности является относительное остаточное сужение (изменение площади сечения в месте разрыва ), определяемое по формуле:
=((Fo-FUI)/Fo)*100% .
Для определения работы, затраченной на пластическую деформацию, сначала определяют площадь S полученной диаграммы растяжения ( OABCDF на рис.2. ). Площадь S определяется любым методом, применяемым в геодезии для определения площадей. Иногда площадь S определяют приближенно, как площадь прямоугольника высотой рв и длиной с учетом коэффициента заполнения диаграммы η= 0,8 – 0,85.
Работа, затраченная на пластическую деформацию, определяется путем умножения площади S полученной диаграммы растяжения на масштаб сил и масштаб удлинений.
Удельная работа (а), определяется делением работы (А) на объем рабочей части образца (V), (a=A/V).
9. РЕКОМЕНДАЦИИ К АНАЛИЗУ РЕЗУЛЬТАТОВ ИСПЫТАНИЙ И ВЫВОДАМ
Выводы из полученных результатов опыта сводятся к определению качества испытанного материала по найденным его механическим характеристикам. Пользуясь справочными таблицами и стандартами, нужно установить марку стали и , в соответствии с этим решить, в каких конструкциях материал может найти применение. Для наглядности следует привести полученные из эксперимента данные и те же данные из справочной литературы для принятой марки стали в виде таблицы.
Источник
