Реактивная сила при растяжении
Главная
Онлайн учебники
База репетиторов России
Тренажеры по физике
Подготовка к ЕГЭ 2017 онлайн
Глава 1. Механика
Силы в природе
1.12. Сила упругости. Закон Гука
При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.
Простейшим видом деформации являются деформации растяжения и сжатия (рис. 1.12.1).
| Рисунок 1.12.1. Деформация растяжения ( x > 0 ) и сжатия ( x < 0 ). Внешняя сила |
При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:
Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жесткостью тела. В системе СИ жесткость измеряется в ньютонах на метр (Н/м). Коэффициент жесткости зависит от формы и размеров тела, а также от материала. В физике закон Гука для деформации растяжения или сжатия принято записывать в другой форме. Отношение ε = x / l называется относительной деформацией, а отношение σ = F / S = –Fупр / S, где S – площадь поперечного сечения деформированного тела, называется напряжением. Тогда закон Гука можно сформулировать так: относительная деформация ε пропорциональна напряжению σ:
Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Модуль Юнга различных материалов меняется в широких пределах. Для стали, например, E ≈ 2·1011 Н/м2, а для резины E ≈ 2·106 Н/м2, т. е. на пять порядков меньше.
Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рис. 1.12.2).
| Рисунок 1.12.2. Деформация изгиба. |
Упругую силу действующую на тело со стороны опоры (или подвеса), называют силой реакции опоры. При соприкосновении тел сила реакции опоры направлена перпендикулярно поверхности соприкосновения. Поэтому ее часто называют силой нормального давления. Если тело лежит на горизонтальном неподвижном столе, сила реакции опоры направлена вертикально вверх и уравновешивает силу тяжести: Сила с которой тело действует на стол, называется весом тела.
В технике часто применяются спиралеобразные пружины (рис. 1.12.3). При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром. Следует иметь в виду, что при растяжении или сжатии пружины в ее витках возникают сложные деформации кручения и изгиба.
В отличие от пружин и некоторых эластичных материалов (резина) деформация растяжения или сжатия упругих стержней (или проволок) подчиняются линейному закону Гука в очень узких пределах. Для металлов относительная деформация ε = x / l не должна превышать 1 %. При больших деформациях возникают необратимые явления (текучесть) и разрушение материала.
 |
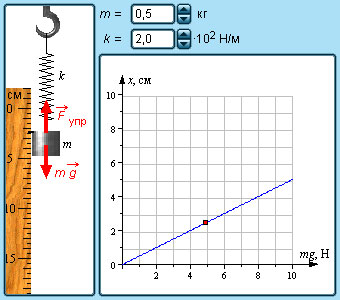Модель. |
Источник
Определение нормальной силы
Центральное растяжение (сжатие) – одно из наиболее простых видов нагружения. Методом сечений в поперечном сечении бруса обнаруживается только один внутренний силовой фактор – нормальная сила. Ее вектор перпендикулярен к поперечному сечению и направлен вдоль продольной оси бруса. Брус, работающий на растяжение-сжатие, принято называть стержнем.
Согласно методу сечений величина и направление продольной силы определяются из уравнения равновесия, составленного для отсеченной части бруса:
(2.9)
Таким образом, продольная (нормальная) сила о произвольном сечении бруса численно равна алгебраической сулеме проекций па продольную ось всех внешних (активных и реактивных) сил, приложенных к отсеченной части.
В общем случае
(2.10)
где 
– интенсивность нагрузки, распределенной вдоль оси бруса на участке от 0 до 
.
Продольная сила 
считается положительной, если она вызывает растяжение, т.е. направлена от сечения. В поперечном сечении бруса она является равнодействующей внутренних нормальных сил, возникающих в этом сечении.
График функции 
называется эпюрой нормальных сил. Из выражения (2.10) следует, что
(2.11)
т.е. интенсивность распределенной нагрузки в каждом сечении равна по величине и знаку тангенсу угла наклона касательной к эпюре 
в соответствующей рассматриваемому сечению точке эпюры.
Нормальные напряжения и деформации
При растяжении (сжатии) бруса в поперечных сечениях возникают только нормальные напряжения. Чтобы задача определения по известным N А имела единственное решение, необходимо установить закон распределения σ(x) по сечению. Для этого используется гипотеза плоских сечений (гипотеза Бернулли): сечения бруса, плоские и нормальные к его оси до деформации, остаются плоскими и нормальными к его оси и при деформации. Поперечные сечения лишь перемещаются вдоль оси, оставаясь параллельными друг другу.
Допустим, брус состоит из бесконечно большого числа продольных волокон. Из гипотезы Бернулли следует, что все волокна деформируются одинаково. Поскольку, согласно закону Гука, равным деформациям соответствуют равные напряжения, то при растяжении (сжатии) бруса нормальные напряжения равномерно распределяются по поперечному сечению, т.е.
;.
Как известно,
. Так как
, то 
. Отсюда
(2.12)
Положительными считаются направления 
, соответствующие растяжению.
В сечениях бруса, примыкающих к месту приложения внешних сил и к закреплениям, распределение напряжений зависит
Рис. 2.7
от способа приложения нагрузки и может быть неравномерным. Поэтому гипотеза плоских сечений в этих местах неверна.
Рассмотрим однородное напряженное состояние бруса, когда напряжения не изменяются по длине (рис. 2.7).
Изменение линейных размеров 
называется абсолютным удлинением; отношение 
– относительным удлинением или линейной деформацией.
В случае неоднородного напряженного состояния линейная деформация определяется выражением 
, где 
– приращение отрезка 
.
Между линейными деформациями 
и вызывающими их напряжениями 
существует связь, обусловленная упругими свойствами материала. Эта связь определяется законом Гука:
(2.13)
где Е – модуль упругости материала.
Рассмотрим выражение
. Согласно формуле (2.13) получим
; поскольку
Отсюда изменение длины всего бруса
(2.14)
Произведение НА называется жесткостью бруса при растяжении (сжатии).
Если законы изменения N и А различны для отдельных участков бруса, то
(2.15)
где 
– число участков.
В частном случае, когда N и А постоянны по длине бруса, получаем формулу Гука в виде
(2.16)
Итак, перемещение i-го сечения с координатой х относительно неподвижного сечения
(2.17)
Аналогично можно записать
(2.18)
где 
– перемещение начального сечения относительно заделки.
Пусть сечение бруса (см. рис. 2.7) имеет форму прямоугольника со сторонами а и b, тогда при растяжении бруса периметр его уменьшится. Величина 
характеризует относительное изменение периметра поперечного сечения и называется поперечной деформацией. Если сечение круглое, то 
. Отношение поперечной деформации к линейной величине постоянно для данного материала и называется коэффициентом Пуассона:
(2.19)
Для стали и большинства металлических материалов 
. В общем случае 
.
Источник
    Äëÿ îòäåëüíî âçÿòîãî ýëåìåíòà êîíñòðóêöèè âçàèìîóðàâíîâåøåííûå àêòèâíàÿ ñèëà è ñèëà ðåàêöèè îïîðû ÿâëÿþòñÿ
âíåøíèìè ñèëàìè.
    Ðàññìîòðèì, êàêèì îáðàçîì êîíñòðóêöèÿ îêàçûâàåò ñîïðîòèâëåíèå âíåøíåé íàãðóçêå, çà ñ÷åò ÷åãî ïðîèñõîäèò èçìåíåíèå
ôîðìû è ðàçìåðîâ êîíñòðóêöèè — äåôîðìèðîâàíèå (îò ëàò. deformatio — èñêàæåíèå).
10.3.1. Ðàñòÿæåíèå
    Íå îáðàùàÿ âíèìàíèå íà òî, êàêèì îáðàçîì, ñ òî÷êè çðåíèÿ êîíñòðóêòèâíîãî ðåøåíèÿ, ïðèëîæåíû âíåøíèå ñèëû Ð,
ðàññìîòðèì ðàñòÿæåíèå ýëåìåíòà êîíñòðóêöèè, ñõåìà íàãðóæåíèÿ êîòîðîãî ïîêàçàíà íà ðèñ. 10.3,à.
|
Ðèñ. 10.3. Óïðîùåííàÿ ìîäåëü äåôîðìàöèè ïðè ðàñòÿæåíèè |
Íà ðèñ. 10.3 ïîêàçàíà òàêæå óïðîùåííàÿ ìîäåëü ìåæàòîìíûõ ñâÿçåé â òâåðäîì òåëå. Æåñòêèå è ïðî÷íûå ìåæàòîìíûå ñâÿçè, ñîåäèíÿþùèå àòîìû
íåäåôîðìèðîâàííîãî òåëà (ðèñ. 10.3,á), ïðè ðàñòÿæåíèè (ðèñ. 10.3,â) ñîçäàþò áîëüøèå
âíóòðåííèå ñèëû ïðîòèâîäåéñòâèÿ âíåøíåé íàãðóçêå, ñòðåìÿùèåñÿ ñîõðàíèòü òåëî êàê åäèíîå öåëîå.
    Ïîä äåéñòâèåì âíåøíèõ ñèë ÷àñòèöû (àòîìû) ìàòåðèàëà, èç êîòîðîãî ñäåëàíà êîíñòðóêöèÿ, áóäóò ïåðåìåùàòüñÿ, è
ïåðåìåùåíèå ÷àñòèö ïîä íàãðóçêîé áóäåò ïðîäîëæàòüñÿ, ïîêà ìåæäó âíåøíèìè è âíóòðåííèìè ñèëàìè íå óñòàíîâèòñÿ ðàâíîâåñèå.
    Òàêîå ñîñòîÿíèå íàçûâàåòñÿ äåôîðìèðîâàííûì
ñîñòîÿíèåì òåëà.
    Ìåðîé âîçäåéñòâèÿ âíåøíèõ ñèë íà àòîìû âåùåñòâà, êîòîðûå óäàëÿþòñÿ äðóã îò äðóãà (ïðè ðàñòÿæåíèè) èëè ñáëèæàþòñÿ
(ïðè ñæàòèè), ò. å. ìåðîé ïðîòèâîäåéñòâèÿ ìàòåðèàëà êîíñòðóêöèè âíåøíåìó ñèëîâîìó âîçäåéñòâèþ, ìåðîé âíóòðåííèõ ñèë â ìàòåðèàëå ÿâëÿåòñÿ
íàïðÿæåíèå. Íàïðÿæåíèåì íàçûâàåòñÿ âíóòðåííÿÿ ñèëà (âîçíèêàþùàÿ ïðè âîçäåéñòâèè âíåøíåé íàãðóçêè),
ïðèõîäÿùàÿñÿ íà åäèíèöó ïëîùàäè â îêðåñòíîñòè äàííîé òî÷êè ðàññìàòðèâàåìîãî ñå÷åíèÿ òåëà:
σ = Ð/F,
| ãäå    | σ |    - | íàïðÿæåíèå, Ïà (1Ïà=1Í/ì2); |
| P |    - | ñóììàðíàÿ ñèëà, Í; | |
| F |    - | ïëîùàäü ïîïåðå÷íîãî ñå÷åíèÿ, ïåðïåíäèêóëÿðíîãî íàïðàâëåíèþ äåéñòâóþùåé ñèëû P,ì2. |
   Â èíæåíåðíîé ïðàêòèêå èíîãäà èçìåðÿþò íàïðÿæåíèÿ â äàÍ/ìì2 (1äàÍ= 10Í).
   Íàïðÿæåíèå, òàêèì îáðàçîì, ïîêàçûâàåò èíòåíñèâíîñòü ïðîòèâîäåéñòâèÿ âíóòðåííèõ ñèë âîçäåéñòâèþ âíåøíåé íàãðóçêè íà
ìåæàòîìíûå ñâÿçè ìàòåðèàëà êîíñòðóêöèè, èëè, ÷òî òî æå ñàìîå, èíòåíñèâíîñòü âîçäåéñòâèÿ âíåøíåé íàãðóçêè íà ìåæàòîìíûå ñâÿçè.
   Åñëè ðàññìîòðåòü äåôîðìèðîâàííîå ñîñòîÿíèå ñòåðæíÿ (áðóñà) (ðèñ. 10.4) ïðè ðàñòÿæåíèè âíåøíèìè ñèëàìè Ð
(ïîêàçàíû íà ðèñóíêå ÷åðíûìè ñòðåëêàìè), òî â ëþáîì ïðîèçâîëüíî âçÿòîì ïîïåðå÷íîì ñå÷åíèè (íàïðèìåð, ïëîñêîñòüþ À) ðàñïðåäåëåíèå
íîðìàëüíûõ íàïðÿæåíèé σ = Ð/F áóäåò ðàâíîìåðíûì.
|
Ðèñ. 10.4. Äåôîðìèðîâàííîå ñîñòîÿíèå áðóñà |
   Ðàâíîäåéñòâóþùàÿ ñèëà íàïðÿæåíèé σ — âíóòðåííÿÿ ñèëà
Ð = σF (íà ðèñ. 10.4 — áåëàÿ ñòðåëêà) — ïðîõîäèò ÷åðåç öåíòð òÿæåñòè ïîïåðå÷íîãî ñå÷åíèÿ âäîëü ëèíèè äåéñòâèÿ
âíåøíåé ñèëû è ðàâíà åé.
   Ïîä äåéñòâèåì ðàñòÿãèâàþùèõ ñèë Ð äëèíà ñòåðæíÿ l óâåëè÷èâàåòñÿ íà âåëè÷èíó Δl,
íàçûâàåìóþ àáñîëþòíûì óäëèíåíèåì. Ðàñòÿæåíèå ñîïðîâîæäàåòñÿ òàêæå óìåíüøåíèåì ïîïåðå÷íûõ ðàçìåðîâ
ñå÷åíèÿ. Ýòî ÿâëåíèå íîñèò íàçâàíèå «ýôôåêò Ïóàññîíà» (ïî èìåíè ôðàíöóçñêîãî ó÷åíîãî è ìåõàíèêà
Ñ. Ïóàññîíà). Àáñîëþòíîå ïîïåðå÷íîå ñóæåíèå
ñòåðæíÿ ïðè ðàñòÿæåíèè Δb =
b — b1; Δc = c — c1.
   Èìåííî çà ñ÷åò èçìåíåíèÿ ôîðìû è ðàçìåðîâ ëþáàÿ êîíñòðóêöèÿ ñîïðîòèâëÿåòñÿ (ñîçäàåò ñèëû ïðîòèâîäåéñòâèÿ) âíåøíèì íàãðóçêàì.
   Â èíæåíåðíîé ïðàêòèêå äåôîðìèðîâàííîå ñîñòîÿíèå ïðèíÿòî îöåíèâàòü íå òîëüêî àáñîëþòíûìè âåëè÷èíàìè èçìåíåíèé ôîðìû
( «ïåðåìåùåíèÿìè»), íî è îòíîñèòåëüíûìè áåçðàçìåðíûìè âåëè÷èíàìè —
«äåôîðìàöèÿìè»:
ε = Δl/l; ε = Δb/b = Δc/c,
| ãäå    | ε |    - | îòíîñèòåëüíîå óäëèíåíèå ïðè ðàñòÿæåíèè; |
| ε’ |    - | îòíîñèòåëüíûå ïîïåðå÷íûå äåôîðìàöèè. |
   Ïðè äîñòàòî÷íî áîëüøèõ âíåøíèõ íàãðóçêàõ (è, êàê ñëåäñòâèå, áîëüøèõ âíóòðåííèõ íàïðÿæåíèÿõ) ìåæàòîìíûå ñâÿçè ìàòåðèàëà ìîãóò
áûòü ðàçîðâàíû, ÷òî ïðèâåäåò ê ðàçðóøåíèþ êîíñòðóêöèè.
   Êîíñòðóêöèÿ äîëæíà áûòü ñïðîåêòèðîâàíà òàê, ÷òîáû îíà íå ðàçðóøèëàñü ïîä íàãðóçêîé. Äåôîðìàöèè (ïåðåìåùåíèÿ), êîòîðûå
íåèçáåæíî âîçíèêàþò â êîíñòðóêöèè ïîä íàãðóçêîé, äîëæíû áûòü âïîëíå îïðåäåëåííûìè è äîñòàòî÷íî ìàëûìè, ïîñêîëüêó âûáðàííûå ðàçìåðû è ôîðìà
ýëåìåíòîâ êîíñòðóêöèè îáåñïå÷èâàþò îïðåäåëåííîå êà÷åñòâî åå ôóíêöèîíèðîâàíèÿ.
   Òàê, èçìåíåíèå ïîä íàãðóçêîé ðàçìåðîâ è ôîðìû ýëåìåíòîâ êîíñòðóêöèè ñàìîëåòà, îáòåêàåìûõ ïîòîêîì âîçäóõà, ñóùåñòâåííûì îáðàçîì
âëèÿåò íà àýðîäèíàìè÷åñêèå õàðàêòåðèñòèêè è, êàê ñëåäñòâèå, — íà ëåòíî-òåõíè÷åñêèå õàðàêòåðèñòèêè ñàìîëåòà.
   Õàðàêòåð ðàáîòû êîíñòðóêöèè ïîä íàãðóçêîé âî ìíîãîì îïðåäåëÿåòñÿ âûáîðîì êîíñòðóêöèîííûõ
ìàòåðèàëîâ. Îäíîé èç îñíîâíûõ õàðàêòåðèñòèê ìàòåðèàëà êîíñòðóêöèè ÿâëÿåòñÿ äèàãðàììà ðàñòÿæåíèÿ (êðèâàÿ äåôîðìèðîâàíèÿ) — âçàèìîçàâèñèìîñòü íàïðÿæåíèé è äåôîðìàöèé
óäëèíåíèÿ, ïîëó÷àåìàÿ â ðåçóëüòàòå èñïûòàíèé îáðàçöîâ ìàòåðèàëîâ íà ðàñòÿæåíèå. Íà ðèñ. 10.5 ïîêàçàí òèïè÷íûé õàðàêòåð äèàãðàìì ðàñòÿæåíèÿ äëÿ
íåêîòîðûõ êîíñòðóêöèîííûõ ìàòåðèàëîâ, ïðèìåíÿåìûõ â ñàìîëåòîñòðîåíèè.
|
Ðèñ. 10.5. Äèàãðàììà ðàñòÿæåíèÿ |
   Ïðÿìîëèíåéíûå íà íåêîòîðîì ïðîòÿæåíèè äèàãðàììû ó÷àñòêè (0-À, 0-ÀÂ) õàðàêòåðèçóþò òàêóþ ñòàäèþ äåôîðìèðîâàíèÿ îáðàçöà,
êîãäà ïðè óâåëè÷åíèè íàãðóçêè äåôîðìàöèè ïðîïîðöèîíàëüíû íàïðÿæåíèÿì è ïðè ñíÿòèè íàãðóçêè èñ÷åçàþò, ò. å. îáðàçåö çà ñ÷åò ìåæàòîìíûõ ñâÿçåé
(ñèë óïðóãîñòè) âîçâðàùàåòñÿ â èñõîäíîå (íåäåôîðìèðîâàííîå) ñîñòîÿíèå. Íà ýòîì ó÷àñòêå ìàòåðèàë «ïîä÷èíÿåòñÿ»
çàêîíó Ãóêà (ïî èìåíè àíãëèéñêîãî åñòåñòâîèñïûòàòåëÿ
Ð. Ãóêà):
σ = Åε,
| ãäå    | σ |    - | íàïðÿæåíèå, Ïà; |
| E |    - | ìîäóëü óïðóãîñòè ìàòåðèàëà, èëè ìîäóëü Þíãà (ïî èìåíè àíãëèéñêîãî ó÷åíîãî Ò.Þíãà), Ïà; | |
| ε |    - | îòíîñèòåëüíîå óäëèíåíèå. |
   Ìîäóëü óïðóãîñòè Å (íàêëîí êðèâîé äåôîðìèðîâàíèÿ â çîíå óïðóãîñòè
0-À (0-ÀÂ) äèàãðàììû: Å = tgα) ÿâëÿåòñÿ ìåðîé óïðóãîñòè («æåñòêîñòè») è õàðàêòåðèçóåò ïîäàòëèâîñòü (ñïîñîáíîñòü ê
äåôîðìèðîâàíèþ) ïîä íàãðóçêîé. Îòìåòèì, ÷òî ñòàëü — áîëåå æåñòêèé, ìåíåå ïîäàòëèâûé ìàòåðèàë, ÷åì àëþìèíèåâûé ñïëàâ.
   Òî÷êà À (ÀÂ) íà äèàãðàììàõ õàðàêòåðèçóåò íàèáîëüøóþ íàãðóçêó Ðïö è, ñîîòâåòñòâåííî,
íàïðÿæåíèÿ
ïðåäåëà ïðîïîðöèîíàëüíîñòè
σïö, ïðè êîòîðûõ åùå ñîáëþäàåòñÿ ëèíåéíàÿ
çàâèñèìîñòü σ — ε.
   Äàëüøå, çà òî÷êîé À (ÀÂ), ëèíåéíàÿ çàâèñèìîñòü σ — ε íàðóøàåòñÿ, ìàòåðèàë äåôîðìèðóåòñÿ («òå÷åò»)
ïîä íàãðóçêîé è ïðè ñíÿòèè íàãðóçêè íå âîçâðàùàåòñÿ ê èñõîäíîìó ñîñòîÿíèþ, â íåì âîçíèêàþò îñòàòî÷íûå ïëàñòè÷åñêèå
äåôîðìàöèè çà ñ÷åò òîãî, ÷òî ÷àñòü ìåæàòîìíûõ ñâÿçåé ðàçðóøàåòñÿ. Òî÷êà  íà äèàãðàììàõ õàðàêòåðèçóåò íàãðóçêó
Ðò è, ñîîòâåòñòâåííî,
íàïðÿæåíèÿ ïðåäåëà òåêó÷åñòè
σò, ïðè êîòîðûõ ìàòåðèàë «òå÷åò» áåç óâåëè÷åíèÿ íàãðóçêè. Íåêîòîðûå ìàòåðèàëû (íàïðèìåð, 4, ñì. ðèñ. 10.5)
èìåþò ÿâíî âûðàæåííóþ ïëîùàäêó òåêó÷åñòè À-Â, ãäå äåôîðìàöèè ñóùåñòâåííî óâåëè÷èâàþòñÿ áåç óâåëè÷åíèÿ
âíåøíåé íàãðóçêè. Äëÿ äðóãèõ ìàòåðèàëîâ (1, 2, 3) ïëîùàäêè òåêó÷åñòè îòñóòñòâóþò, â ýòîì ñëó÷àå òî÷êè À è  íà äèàãðàììå ïðàêòè÷åñêè
ñîâïàäàþò.
   Çîíà Â-Ñ äèàãðàììû íàçûâàåòñÿ çîíîé óïðî÷íåíèÿ. Çäåñü ïîñëå ñòàäèè òåêó÷åñòè
ìàòåðèàë ñíîâà ïðèîáðåòàåò ñïîñîáíîñòü óâåëè÷èâàòü ñîïðîòèâëåíèå äàëüíåéøåé äåôîðìàöèè, îäíàêî äëÿ óäëèíåíèÿ îáðàçöà â ýòîé çîíå òðåáóåòñÿ â
ñîòíè ðàç áîëåå ìåäëåííîå íàðàñòàíèå íàãðóçêè, ÷åì â çîíå óïðóãèõ äåôîðìàöèé.
|
Ðèñ. 10.6. Äèàãðàììà èñòèííûõ íàïðÿæåíèé |
   Òî÷êà Ñ äèàãðàììû õàðàêòåðèçóåò ìàêñèìàëüíóþ (ïðåäåëüíóþ) íàãðóçêó Ðmax è, ñîîòâåòñòâåííî,
íàïðÿæåíèÿ ïðåäåëà ïðî÷íîñòè èëè íàïðÿæåíèÿ âðåìåííîãî ñîïðîòèâëåíèÿ σâ, ïðè êîòîðûõ åùå ñîõðàíÿåòñÿ öåëîñòíîñòü
ýëåìåíòà êîíñòðóêöèè, íàãðóæåííîãî ðàñòÿæåíèåì.
   Äàëüøå, çà òî÷êîé Ñ äèàãðàììû, áåç óâåëè÷åíèÿ âíåøíåé íàãðóçêè èäåò ëàâèíîîáðàçíîå ðàçðóøåíèå ìåæàòîìíûõ ñâÿçåé
ìàòåðèàëà.
   Íàïðÿæåíèå σâ, òàêèì îáðàçîì, õàðàêòåðèçóåò ïðî÷íîñòü ìàòåðèàëà íà ðàçðûâ.
   Òî÷êà D äèàãðàììû õàðàêòåðèçóåò ðàçðóøåíèå (ðàçðûâ) îáðàçöà. Íèñõîäÿùàÿ âåòâü äèàãðàììû Ñ-D èìååò óñëîâíûé
õàðàêòåð, ïîñêîëüêó íàïðÿæåíèÿ ðàññ÷èòûâàþòñÿ äëÿ ïëîùàäè ïîïåðå÷íîãî ñå÷åíèÿ èñõîäíîãî îáðàçöà. Ðåàëüíî íàïðÿæåíèÿ ðàñòóò, ÷òî ïîêàçûâàåò
äèàãðàììà èñòèííûõ íàïðÿæåíèé (ðèñ. 10.6 — ïóíêòèðíàÿ ëèíèÿ),
â êîòîðîé íàïðÿæåíèÿ ðàññ÷èòûâàþòñÿ äëÿ èñòèííîé ïëîùàäè ïîïåðå÷íîãî ñå÷åíèÿ îáðàçöà.  èíòåðâàëå Î-À ðîñò íàïðÿæåíèÿ èäåò áåç
ðàçðóøåíèÿ ìåæàòîìíûõ ñâÿçåé, ïîñëå ñíÿòèÿ íàãðóçêè îáðàçåö âîçâðàùàåòñÿ ê èñõîäíîìó ñîñòîÿíèþ. Â èíòåðâàëå À-D ðîñò íàïðÿæåíèÿ
ïðîèñõîäèò çà ñ÷åò ðàçðóøåíèÿ ìåæàòîìíûõ ñâÿçåé è çíà÷èòåëüíîãî ìåñòíîãî óòîíåíèÿ îáðàçöà (îáðàçîâàíèÿ
øåéêè 1).  ìîìåíò ðàçðóøåíèÿ (òî÷êà D äèàãðàììû) ïëîùàäü ïîïåðå÷íîãî ñå÷åíèÿ ïëàñòè÷åñêè
äåôîðìèðîâàííîãî îáðàçöà ìåíüøå èñõîäíîé.
   Ïðî÷íîñòü êîíñòðóêöèè, åñòåñòâåííî, çàâèñèò îò ïðî÷íîñòè ìàòåðèàëà, èç êîòîðîãî îíà èçãîòîâëåíà.
   Ïðî÷íîñòü
(íåñóùàÿ ñïîñîáíîñòü)
êîíñòðóêöèè — ýòî ñïîñîáíîñòü êîíñòðóêöèè â îïðåäåëåííûõ óñëîâèÿõ âîñïðèíèìàòü (âûäåðæèâàòü) áåç
ðàçðóøåíèÿ âíåøíèå íàãðóçêè.
Íàãðóçêà, ïðè êîòîðîé ïðîèñõîäèò ðàçðóøåíèå êîíñòðóêöèè, íàçûâàåòñÿ
ðàçðóøàþùåé.
|
Ðèñ. 10.7. Òðàåêòîðèè íàïðÿæåíèé |
   Íåñóùàÿ ñïîñîáíîñòü âî ìíîãîì çàâèñèò îò ïëàñòè÷íîñòè ìàòåðèàëà. Ïëàñòè÷íîñòü
— ñïîñîáíîñòü ìàòåðèàëà ïîëó÷àòü áîëüøèå îñòàòî÷íûå äåôîðìàöèè, íå ðàçðóøàÿñü. Õðóïêîñòü
(ñâîéñòâî, ïðîòèâîïîëîæíîå ïëàñòè÷íîñòè) — ñïîñîáíîñòü ìàòåðèàëà ðàçðóøàòüñÿ áåç çàìåòíîé ïëàñòè÷åñêîé äåôîðìàöèè.
   Æåñòêîñòü — ñïîñîáíîñòü êîíñòðóêöèè ñîïðîòèâëÿòüñÿ äåéñòâèþ âíåøíèõ íàãðóçîê
ñ äîïóñòèìûìè â ýêñïëóàòàöèè äåôîðìàöèÿìè, íå íàðóøàþùèìè ðàáîòîñïîñîáíîñòü êîíñòðóêöèè.
   Íåñóùàÿ ñïîñîáíîñòü êîíñòðóêöèè ðåçêî ñíèæàåòñÿ èìåþùèìèñÿ â ìàòåðèàëå êîíñòðóêöèè ìèêðîòðåùèíàìè, âêðàïëåíèÿìè
èíîðîäíûõ ìàòåðèàëîâ, íàðóøàþùèìè ïîñòîÿíñòâî íàïðÿæåíèé.
   Êîíöåíòðàòîðû íàïðÿæåíèé
— ìåñòíûå ðåçêèå èçìåíåíèÿ îäíîðîäíîñòè (ôîðìû è, ñëåäîâàòåëüíî, æåñòêîñòè) êîíñòðóêöèè, ïðèâîäÿùèå ê ðåçêîìó ìåñòíîìó
(ëîêàëüíîìó) ïîâûøåíèþ íàïðÿæåíèé â êîíñòðóêöèè.
   Íà ðèñ. 10.7 ïîêàçàíî äåéñòâèå ðàñòÿãèâàþùåé âíåøíåé íàãðóçêè, ðàâíîìåðíî ðàñïðåäåëåííîé ïî êðàÿì ïðîñòåéøèõ êîíñòðóêòèâíûõ
ýëåìåíòîâ — ëèñòîâ. Ïóíêòèðíûå ëèíèè ïðåäñòàâëÿþò ñîáîé òàê íàçûâàåìûå òðàåêòîðèè íàïðÿæåíèé, âäîëü êîòîðûõ íàïðÿæåíèå ïåðåäàåòñÿ îò
ìîëåêóëû ê ìîëåêóëå. Äëÿ ãëàäêîãî ëèñòà ýòè ëèíèè ïàðàëëåëüíû, íàïðÿæåíèÿ â ëþáîì ñå÷åíèè ëèñòà îäèíàêîâû.
|
Ðèñ. 10.8. ïåðåäà÷à íàãðóçêè â ñîåäèíåíèè |
   Ñèëû, ïåðåäàþùèåñÿ ïî òðàåêòîðèÿì íàïðÿæåíèé â ëèñòàõ ñ êîíöåíòðàòîðàìè (íàäðåç â êðîìêå ëèñòà, îòâåðñòèå â öåíòðå ëèñòà),
îáõîäÿò ðàçðûâ â ìàòåðèàëå. Ïëîòíîñòü òðàåêòîðèé íàïðÿæåíèé óâåëè÷èâàåòñÿ, è ëîêàëüíûå íàïðÿæåíèÿ σ ó êðàÿ êîíöåíòðàòîðà âîçðàñòàþò
(èíîãäà ìíîãîêðàòíî). Â ýòèõ ìåñòàõ ìîæåò ïðîèçîéòè íàðóøåíèå (ðàçðûâ) ìåæàòîìíûõ ñâÿçåé, âîçíèêíóò ìèêðîòðåùèíû, ðàñïðîñòðàíåíèå êîòîðûõ âåäåò
ê ðàçðóøåíèþ êîíñòðóêöèè.
   Ðàñïðåäåëåíèå íàïðÿæåíèé â çàêîíöîâêàõ (ìåñòàõ ñîåäèíåíèÿ äåòàëåé)
îáû÷íî îñîáåííî
ñëîæíî, â íèõ îáÿçàòåëüíî ïîÿâëÿþòñÿ êîíöåíòðàöèè íàïðÿæåíèé
— ìåñòíîå ïîâûøåíèå íàïðÿæåíèé.
   Â ìåñòå ñîåäèíåíèÿ (ðèñ. 10.8) ëèñòîâ 1 è 3 ñ ïîìîùüþ çàêëåïîê (èëè ñâàðíûõ òî÷åê) 2 ïåðåäà÷à
íàãðóçêè áóäåò
ïðîèñõîäèòü òîëüêî ÷åðåç òî÷êè êðåïëåíèÿ. Ëèñòû ðàâíîìåðíî âêëþ÷àòñÿ â ðàáîòó íà äîñòàòî÷íî áîëüøîì óäàëåíèè îò ìåñòà
ñîåäèíåíèÿ.
   Çàøòðèõîâàííàÿ îáëàñòü ëèñòîâ ïðàêòè÷åñêè âûêëþ÷åíà èç ðàáîòû è íå èñïûòûâàåò íàïðÿæåíèé.  òî æå âðåìÿ
íàïðÿæåíèÿ â ïîïåðå÷íûõ ñå÷åíèÿõ ëèñòîâ ðàñïðåäåëåíû íåðàâíîìåðíî, ïðè÷åì σÀ-À > σÁ-Á > σÂ-Â.
   Êîíñòðóêòîð îñîáîå âíèìàíèå äîëæåí óäåëÿòü âûáîðó ôîðìû äåòàëåé, ðàáîòàþùèõ íà ðàñòÿæåíèå, è îñîáåííî èõ
çàêîíöîâîê, ÷òîáû óìåíüøèòü âîçìîæíûå êîíöåíòðàöèè íàïðÿæåíèé.
Источник