Разрушающее напряжение при статическом растяжении
1. Механические характеристики
Надёжность работы электрических машин, аппаратов и установок зависит от качества и правильного выбора соответствующих электротехнических материалов. При рациональном выборе электротехнических материалов можно создать электрооборудование малых габаритов и массы, надёжное в эксплуатации. Но для этого необходимо знать свойства электротехнических материалов и их изменения под воздействием электрического напряжения, температуры и других факторов.
Величины, с помощью которых оценивают те или иные свойства материалов, называют характеристиками. Чтобы полностью оценить свойства того или иного электротехнического материала, необходимо знать его механические, электрические, тепловые и физико-химические характеристики. У магнитных материалов – магнитные.
К основным механическим характеристикам материала относятся:
- Разрушающее напряжение при растяжении δр,
- Разрушающее напряжение присжатии δс,
- Разрушающее напряжение при статическом изгибе δи,
- Ударная вязкость а
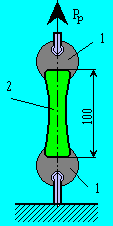
Разрушающее напряжение при растяжении δропределяют на образцах материала определенной формы, при которой обеспечивается равномерное распределение растягивающего усилия по площади сечения в средней части образца. Образец 2 утолщёнными концами закрепляют в стальных зажимах (захватах) 1 испытательной машины (рис). Нижний зажим машины неподвижен, а к другому прикладывают разрушающее (растягивающее) усилие Рр, которое плавно нарастает с определённой скоростью до момента разрыва образца.
Видео об испытании механических характеристик
Рассчитывается по формуле: δр = (Мпа)
где Р – разрушающее усилие при разрыве образца, Н; S площадь поперечного сечения образца до испытания, м2.
Разрушающее напряжение при сжатии δс, определяется на образцах, имеющих форму цилиндра или куба. Так, у формованных и прессованных пластмасс эта характеристика определяется на образцах, представляющих собой сплошные цилиндры высотой 15 мм и диаметром 10 мм.
Образец располагают между стальными плитами испытательного пресса, к которым прикладывают сжимающую нагрузку. Последнюю повышают с определенной скоростью до момента разрушения образца.
Рассчитывается по формуле: δc = (Мпа)
где Р – разрушающее усилие при разрыве образца, Н; S площадь поперечного сечения образца до испытания, м2.
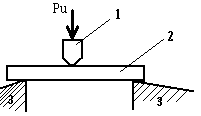
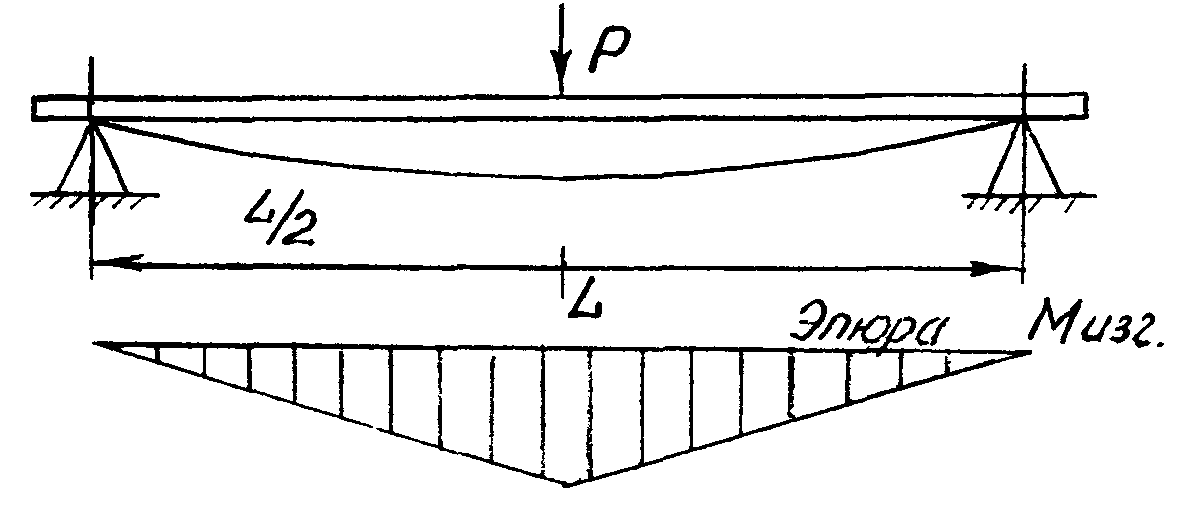
Разрушающее напряжение при статическом изгибе δи определяется на образцах, представляющих собой бруски прямоугольного сечения. Образец 2 материала (рис) помещают в испытательную машину, где он своими концами свободно опирается на две стальные опоры 3. Изгибающее усилие Ри прикладываемое к середине образца 2 через стальной наконечник 1, плавно увеличивают и доводят до величины, при которой происходит разрушение образца.
Рассчитывается по формуле: δи = 1,5 Ри L / (b h)2 (Мпа)
где Ри – изгибающее усилие, Н; L – расстояние между стальными опорами в испытательной машине, м; b и h – ширина и толщина образца м.
Ударная вязкость — α –характеризуется способностью материала сопротивляться ударным нагрузкам и определяется отношением работы ∆А, затраченной на разрушение образца, к площади его первоначального сечения Sо:
α = ∆ А/ Sо (Дж/м2)
Чем меньше ударная вязкость, тем более хрупок данный материал.
Источник
Отвечает эксперт ЗАО ЦНИИПСК им. Мельникова
Испытание на растяжение металла заключаются в растяжении образца с построением графика зависимости удлинения образца (Δl) от прилагаемой нагрузки (P), с последующим перестроением этой диаграммы в диаграмму условных напряжений (σ — ε)
Испытания на растяжение проводятся по ГОСТ 1497, по этому же ГОСТу определяются и образцы на которых проводятся испытания.
Как уже говорилось выше, при испытаниях строится диаграмма растяжения металла. На ней есть несколько характерных участков:
- Участок ОА — участок пропорциональности между нагрузкой Р и удлинением ∆l. Это участок, на котором сохраняется закон Гука. Данная пропорциональность была открыта Робертом Гуком в 1670 г. и в дальнейшем получила название закона Гука.
- Участок ОВ — участок упругой деформации. Т.е., если к образцу приложить нагрузку, не превышающую Ру, а потом разгрузить, то при разгрузке деформации образца будут уменьшаться по тому же закону, по которому они увеличивались при нагружении
Выше точки В диаграмма растяжения отходит от прямой — деформация начинает расти быстрее нагрузки, и диаграмма принимает криволинейный вид. При нагрузке, соответствующей Рт (точка С ), диаграмма переходит в горизонтальный участок. В этой стадии образец получает значительное остаточное удлинение практически без увеличения нагрузки. Получение такого участка на диаграмме растяжения объясняется свойством материала деформироваться при постоянной нагрузке. Это свойство называется текучестью материала, а участок диаграммы растяжения, параллельный оси абсцисс, называется площадкой текучести.
Иногда площадка текучести носит волнообразный характер. Это чаще касается растяжения пластичных материалов и объясняется тем, что вначале образуется местное утонение сечения, затем это утонение переходит на соседний объем материала и этот процесс развивается до тех пор, пока в результате распространения такой волны не возникает общее равномерное удлинение, отвечающее площадке текучести. Когда имеется зуб текучести, при определении механических свойств материала, вводят понятия о верхнем и нижнем пределах текучести.
После появления площадки текучести, материал снова приобретает способность сопротивляться растяжению и диаграмма поднимается вверх. В точке D усилие достигает максимального значения Pmax. При достижении усилия Pmax на образце появляется резкое местное сужение — шейка. Уменьшение площади сечения шейки вызывает падение нагрузки и в момент, соответствующий точке K диаграммы, происходит разрыв образца.
Прилагаемая нагрузка для растяжения образца зависит от геометрии этого образца. Чем больше площадь сечения, тем более высокая нагрузка необходима для растяжения образца. По этой причине, получаемая машинная диаграмма не дает качественной оценки механических свойств материала. Чтобы исключить влияние геометрии образца, машинную диаграмму перестраивают в координатах σ − ε путем деления ординат P на первоначальную площадь сечения образца A0 и абсцисс ∆l на lо. Перестроенная таким образом диаграмма называется диаграммой условных напряжений. Уже по этой, новой диаграмме, определяют механические характеристики материала.
Определяются следующие механические характеристики:
Предел пропорциональности σпц – наибольшее напряжение, после которого нарушается справедливость закона Гука σ = Еε , где Е – модуль продольной упругости, или модуль упругости первого рода. При этом Е =σ/ε = tgα , т. е. модуль E это тангенс угла наклона прямолинейной части диаграммы к оси абсцисс
Предел упругости σу — условное напряжение, соответствующее появлению остаточных деформаций определенной заданной величины (0,05; 0,001; 0,003; 0,005%); допуск на остаточную деформацию указывается в индексе при σу
Предел текучести σт – напряжение, при котором происходит увеличение деформации без заметного увеличения растягивающей нагрузки
Также выделяют условный предел текучести — это условное напряжение, при котором остаточная деформация достигает определенной величины (обычно 0,2% от рабочей длины образца; тогда условный предел текучести обозначают как σ0,2). Величину σ0,2 определяют, как правило, для материалов, у которых на диаграмме отсутствует площадка или зуб текучести
Предел прочности (временное сопротивление разрыву) σв – напряжение, соответствующее наибольшей нагрузке Pmax , предшествующей разрыву образца
Кроме характеристик прочности материала, при испытании на растяжение определяют также характеристики пластичности — относительное удлинение δ и относительное сужение ψ
где lо – первоначальная расчетная длина образца, а lк – конечная расчетная длина образца
Источник
42
ЛЕКЦИЯ
4,5
Основными
механическими характеристиками
материалов являются:
—
разрушающее напряжение при сжатии σс;
—
разрушающее напряжение при растяжении
σр:
—
разрушающее напряжение при статическом
изгибе σи;
—
ударная вязкость а.
Все эти механические характеристики в
основном определяют конструкционную
прочность деталей машин и приборов по
отношению к действию механических
нагрузок в процессе эксплуатации.
Разрушающее
напряжение при сжатии σс
,(при испытании материалов эту
характеристику называют пределом
прочности при сжатии) определяют на
специальных образцах, имеющих форму
цилиндра или куба.
σс
= Pc/So
МПа,
где
РС-
разрушающее усилие при сжатии стандартного
образца.
Разрушающее
напряжение при растяжении
σр
(при испытании материалов эту характеристику
называют пределом прочности или временным
сопротивлением материала при растяжении.
σр=
Pp/Fo
МПа,
где
Рр
— разрушающее усилие при разрыве
стандартного образца.
Данную характеристику
определяют на специальных разрывных
машинахна стандартных
образцах такой формы, при которой
обеспечивается равномерное распределение
растягивающего усилия по площади сечения
образца в его средней части.
Разрушающее
напряжение при статическом изгибе σи(прииспытании
материалов эту
характеристику называют пределом
прочности при статическом изгибе).
σи
=1,5PиL/
bh
; σи=Wmax/
W,
где
Wmax
-максимальный изгибающий момент (Wmax
= Pmax
L/4).
W=b2h/
6 (для прямоугольного сечения).
W
= 3,14d3/32
(для образца круглого сечения).
Ударная
вязкость
«а» определяется как отношение работы
А, затраченной маятником испытательной
машины (копра) на разрушение специального
образца, к площади его поперечного
сечения Fo.
а=A/Fo
(Дж/м2)
Чем меньше ударная
вязкость, тем более хрупок материал.
Ударная вязкость определяется в
результате динамических испытаний
материалов при однократном нагружении.
Разрушающие
напряжения при сжатии растяжении и
статическом изгибе определяются в
результате испытаний материалов при
статическом однократном нагружении.
Наряду с рассмотренными
характеристиками и видами испытаний
материалов существуют и другие
характеристики и соответствующие им
специальные виды испытаний: циклические
испытания, специальные испытания на
жаростойкость, коррозионостойкость,
износостойкость, вибростойкость и др.,
которые позволяют определить функциональные
и
эксплуатационные
характеристики рассматриваемых
материалов. Более подробно закономерности,
определяющие строение и свойства
материалов в зависимости от их состава
и условий обработки рассматриваются в
спецдисциплине «Материаловедение».
ЭЛЕКТРИЧЕСКИЕ
ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ.
Основным свойством вещества по отношению
к электрическому полю является
электропроводностьт.е. способность
проводить электрический ток под
воздействием постоянного (не изменяющегося
во времени) электрического напряжения.
Любой электротехнический материал-
проводник, полупроводник и даже диэлектрик
— проводит электрический ток.
Если
вещество находится в электрическом
поле с напряженностью Е, то имеющиеся
в веществе свободные заряженные частицы
— носители
зарядов —
под действием силы F=qЕ,
где q-заряд
частицы, приобретают ускорение в
направлении вектора Е (для носителей,
имеющих положительный заряд «+q»)
или в противоположном направлении (для
носителей с отрицательным зарядом
«-q»). Возникающее таким образом
упорядоченное в пространстве (в отличие
от хаотического теплового) движение
электрических зарядов и есть электрический
ток в веществе.
Для
оценки степени электропроводности того
или иного материала необходимо
определить его удельное
электрическое
сопротивление
ρ
ρ=R
S/L;
где
R
-общее электрическое сопротивление
образца, Ом;
L
-длина пути тока в образце материала,
м;
S
-площадь сечения образца материала,
через которую протекают токи
проводимости, м2.
Величина,
обратная сопротивлению, называется
электрической
проводимостью.
γ= 1/ρ.
Проводимость
измеряется в сименсах, в честь немецкого
физика Сименса.
Удельная проводимость
и удельное сопротивление определяют
плотность тока в веществе при заданной
напряженности электрического поля,
т.е. количественно характеризуют явление
электропроводности.
Значения их у
различных электротехнического материалов
резко отличаются. У веществ в сверхпроводящем
состоянии удельное сопротивление
равно нулю, а у разреженных газов, при
отсутствии в них электрического разряда
стремится к бесконечности.
Удельное
сопротивление металлических проводников
очень мало (10-8…10-б
Ом м),
что указывает на большую электрическую
проводимость проводниковых материалов.
Удельное сопротивление полупроводниковых
материалов(полупроводников) больше,
чем проводников (10-4…108
Ом м),а
диэлектриков еще больше (108…1018
Ом м).
Большое удельное
сопротивление диэлектриков указывает
на их весьма малую проводимость.
Однако,
при классификации веществ по электрическим
свойствам (проводники, полупроводники,
диэлектрики), кроме значения ρ необходимо
учитывать и физическую природу
электропроводности, в частности, вид
свободных носителей заряда и характер
зависимости ρ от температуры. Необходимо
также иметь ввиду, что в зависимости от
структуры и внешних условий порядок
значений ρ вещества может различаться
весьма существенно. Так, углерод в
аллотропической модификации графита
— проводник, а в модификации алмаза —
диэлектрик; твердые и жидкие металлы
— проводники, но пары металлов —
диэлектрики; типичные (для нормальных
условий) полупроводники германий Ge
и кремний Si
при воздействии очень высоких
гидростатических
давлений становятся проводниками, а —
при воздействии
очень
низких температур — диэлектриками.
Зависимость
удельного электрического сопротивления
проводников, полупроводников и
диэлектриков от температуры может быть
представлена графически (рис.1).
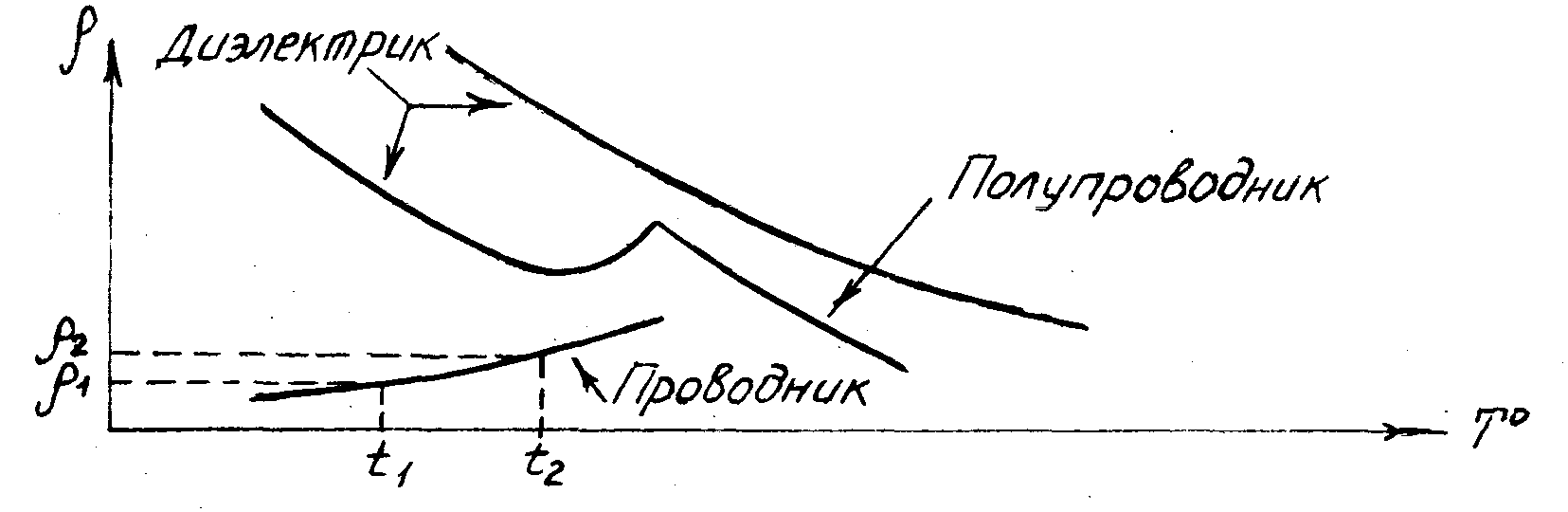
Рис. 1. Зависимость
ρ от температуры.
Температурный
коэффициент удельного сопротивления
ТКρ.
Эта
характеристика позволяет оценить
изменение удельного электрического
сопротивления материала при изменении
температуры. При линейном изменении
удельного сопротивления (в узком
диапазоне температур)
TKρ(α)=(p2-p1)/
[p1(t2-t1)];
здесь:
ρ1
и ρ2-удельные
электрические сопротивления материала
при начальной t1
и температуре t2.
Kaк
видно из рисунка 1,ТКρ
проводников больше нуля, что указывает
на рост электрического сопротивления
проводников с повышением температуры.
У полупроводников и диэлектриков
ТКρ
меньше нуля, что указывает на уменьшение
сопротивления этих материалов с
повышением температуры.
Диэлектрическая
проницаемость
εr.
Эта
характеристика позволяет определить
способность диэлектрика при нанесении
на него электродов и подаче напряжения
образовывать электрическую
емкость.
Электрическая
ёмкость “C”
плоского конденсатора с двумя
металлическими электродами
прямопропоциональна диэлектрической
проницаемости, т.е.
C=εo
*εr*
S/h,
где:
— h
-толщина диэлектрика, м;
—
S
-площадь одного металлического электрода,
м2;
—
εo-электрическая
постоянная (εo=8,85416*
10-12Ф/м);
—
εr-диэлектрическая
проницаемость.
Диэлектрическая
проницаемость электроизоляционных
материалов зависит от интенсивности
процессов поляризации,
протекающих в диэлектриках под действием
приложенного напряжения.
Различают четыре
основных вида поляризации диэлектриков:
электронную, дипольную, ионную и
спонтанную. Более подробно эти виды
будут рассмотрены при рассмотрении
свойств диэлектриков.
Диэлектрическая
проницаемость зависит от температуры.
График зависимости εr=f
(Т) проставлен на рис.2.
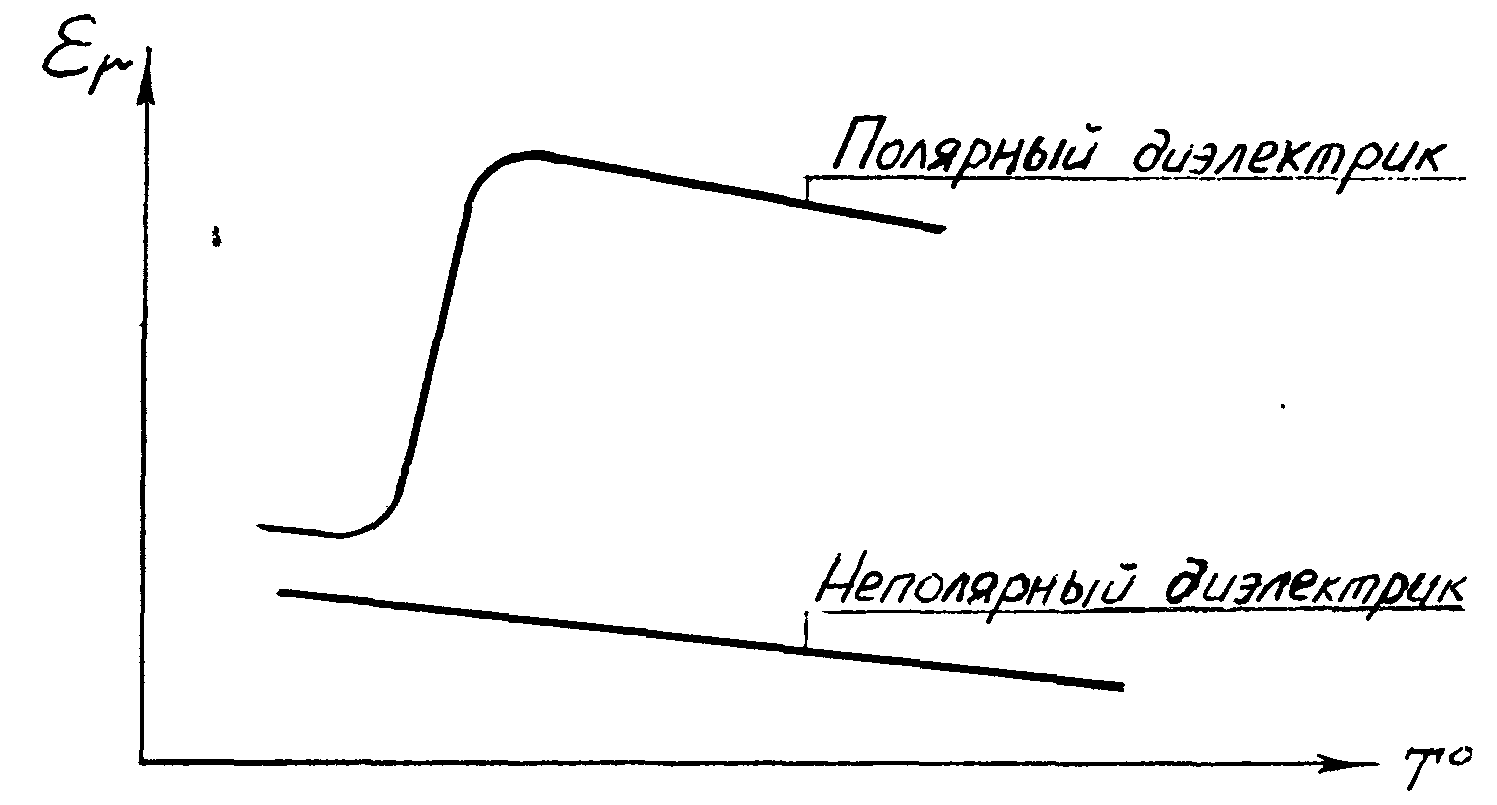Рис.2.
Зависимость εr от Т .
Поскольку
в неполярных диэлектриках происходит
только электронная
поляризация,
их диэлектрическая проницаемость
невелика (1-2,2).В полярных диэлектриках
интенсивность поляризации больше, чем
в нейтральных, так как в них осуществляется
два вида поляризации: дипольная и
электронная, поэтому величина ε
составляет порядка 3-8.
Следует отметить,
что диэлектрическая проницаемость
электроизоляционных материалов
изменяется не только от температуры,
но и
от частоты
приложенного напряжения, давления,
влажности и др. факторов.
Тангенс
угла диэлектрических потерь tgδ.
При воздействии
электрического поля на любое вещество
в последнем наблюдается рассеяние
некоторого количества электрической
энергии, превращающейся в тепловую.
Обычно говорят о «потерях», имея
в виду среднюю за некоторый промежуток
времени рассеиваемую электрическую
мощность.
Если
к обрезку металлического проводника
подключить постоянное напряжение
или переменное, действующее значение
которого равно постоянному, то потери
энергии в том и другом случае будут
одинаковы, т.е. Р ==Р
~
.
Если
же такой опыт провести с диэлектриком,
то потери энергии в нем при переменном
напряжении будут во много раз больше
потерь энергии при постоянном напряжении,
т. e.P~»P=.
Потери энергии в диэлектрике называются
диэлектрическими
потерями
(активная мощность). В диэлектрике,
помещенном в переменное синусоидальное
электрическое поле с напряженностью Е
и угловой частотой ω возникают
электрические токи двух видов: ток
смещения Iсм
и ток проводимости Iпр.
Плотность тока смещения
Iсм=j*ω*ε0*ε*E.
плотность тока
проводимости
Iпр=γаЕ.
где
γа-
удельная активная проводимость
диэлектрика на угловой частоте ω.
Плотность общего тока равна векторной
сумме плотностей токов смещения и
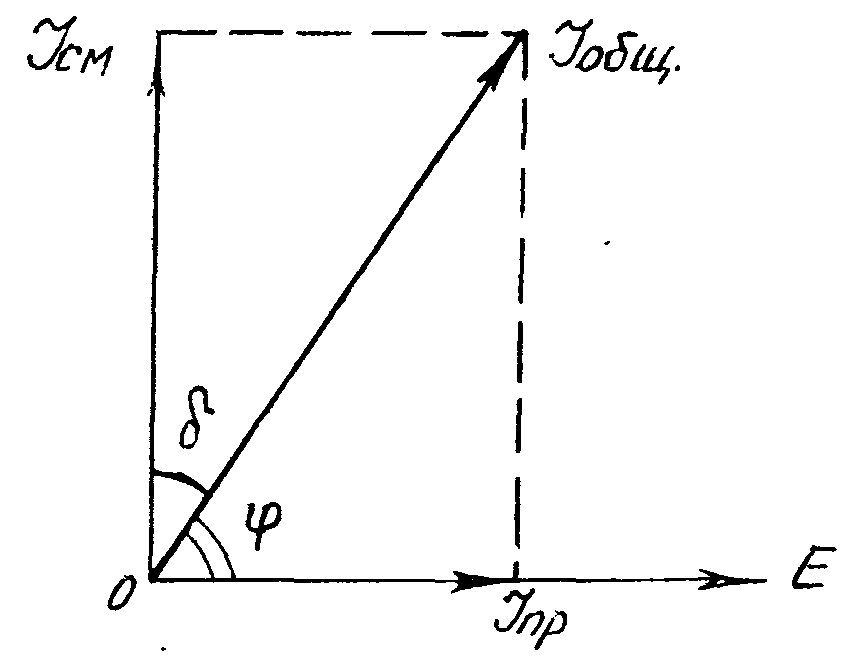
проводимости (рис.3).
Рис.3. Векторная диаграмма токов в
диэлектрике
на комплексной
плоскости.
Если
бы диэлектрик был идеальным, т.е. без
потерь (γа
= 0), то был бы чисто реактивным и его
плотность
I
= Icм=
j*ωε0εЕ
была бы направлена по мнимой оси под
углом 90° к вектору Е. Однако, у реальных
диэлектриков с удельной активной
проводимостью на частоте ω отличной
от нуля, суммарный ток сдвинут на угол
δ = 90°-φ относительно тока идеального
диэлектрика (φ-угол сдвига фаз между
током и напряжением).
Чем
больше удельная активная проводимость
диэлектрика, тем больше угол δ,
характеризующий степень отличия
реального диэлектрика от идеального.
Угол δ между векторами плотностей
переменного тока диэлектрика и тока
смещения на комплексной плоскости
называют углом диэлектрических
потерь.
Тангенс этого угла
tgδ
= Inp/Icм
= γa/ωεoε
является одним из важнейших параметров
не только диэлектриков, но, также
конденсаторов, изоляторов и других
электроизоляционных элементов.
Мощность, рассеиваемая
в единице объема вещества, так называемые
удельные диэлектрические потери
определятся как:
P=γa•E2=
ω*ε0*ε*Е2
tgδ (Вт/м3).
Чем
выше tgδ
,тем больше нагрев диэлектрика в
электрическом поле заданной частоты и
напряженности.
Введение
безразмерного параметра tgδ
удобно потому, что он не зависит от формы
и размеров участка изоляции, а определяется
лишь свойствами диэлектрического
материала. Полные диэлектрические
потери в диэлектрике с емкостью С
(активная мощность, теряемая в диэлектрике)
при приложении напряжения U
с угловой частотой ω= 2πf,
где f-частота,
Гц, определится по формуле:
Pa=U2*πf*C*tgδ,
таким
образом, tgδ
определяет потери в диэлектриках.
Наряду
с потерями tgδ характеризует добротность
конденсаторов и, следовательно,
максимальную добротность контура с
данным конденсатором (Q=l/tgδ).
Высокие диэлектрические
потери приводят к разогреву и тепловому
пробою диэлектриков в сильном электрическом
поле, снижению добротности и избирательности
колебательных контуров. В связи с этим
стремятся снизить tgδ диэлектрических
материалов, что возможно, если известны
природа диэлектрических потерь.
Следует различать
механизм диэлектрических потерь на
электропроводность от релаксационных
потерь резонансных и ионизационных.
Тот или иной механизм потери мощности
в диэлектрике зависит как от состава
диэлектрика, так и от параметров внешнего
электрического поля, на него
воздействующего.
В условиях размещения
диэлектрика в электрическом поле не
очень высокой напряженности физические
явления, происходящие в нем при этом,
практически оставляют диэлектрик
непроводящей средой.
Однако силы
электрического поля при соответствующем
увеличении напряженности могут
привести к нарушению такого состояния.
В результате диэлектрик из непроводящего
состояния перейдет в состояние
высокой проводимости в узком канале,
направленном от электрода к электроду.
Явление образования в диэлектрике
проводящего канала под действием
электрического поля называют пробоем.
Минимальное
приложенное к образцу диэлектрика
напряжение, приводящее к его пробою,
называют пробивным напряжением Uпр.
Напряженность однородного поля (поля,
в котором напряженность во всех точках
одинакова) при котором происходит
пробой-разрушение диэлектрика с
образованием в нем сквозного канала с
очень большой проводимостью — называют
электрической прочностью диэлектрика,
которую рассчитывают по формуле:
Enp=
Unp/h
(В/м),
где
Unp-пробивное
напряжение;
h-
толщина диэлектрика в месте пробоя. В
виду того, что диэлектрики пробиваются
при очень больших напряжениях (тысячи
вольт), значение электрической прочности
выражают в мегавольтах на метр толщины
материала в месте пробоя (МВ/м).
Вольт-амперная
характеристика образца диэлектрика
или электрической изоляции линейна при
обычных напряжениях и отклоняется
от линейной с приближением к пробивному
напряжению, а в момент пробоя ток
через диэлектрик резко возрастает, так
что dI/dU→∞(рис.
4).
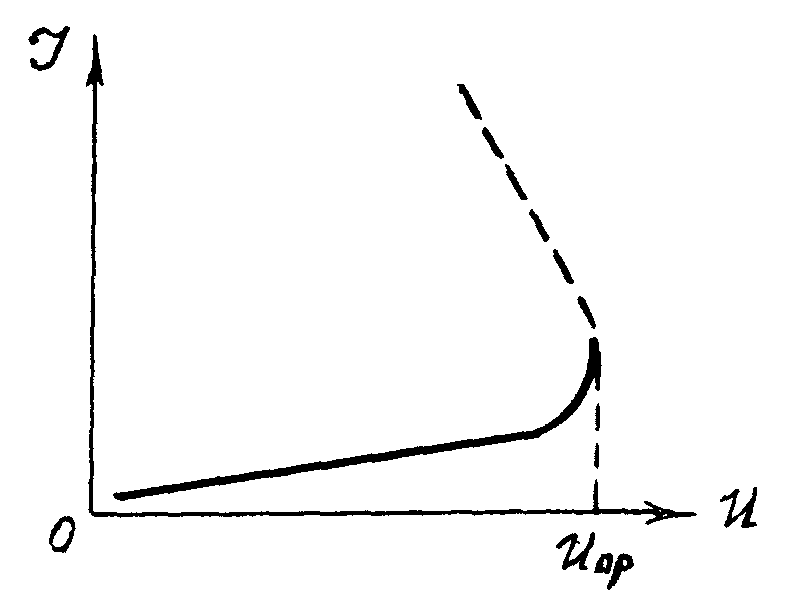Рис.
4. ВАХ образца диэлектрика.
В месте пробоя
возникает искра или электрическая дуга.
Вследствие образования плазменного
сильно проводящего канала между
электродами образец оказывается
короткозамкнутым, и напряжение на
нем падает несмотря на рост тока.
Номинальное
напряжение электрической изоляции
должно быть меньше пробивного напряжения.
Величину, равную отношению пробивного
напряжения к номинальному напряжению,
называют коэффициентом
запаса электрической прочности.
Значение
Unp
диэлектрика непосредственно связано
со временем приложения напряжения.
Так при кратковременных импульсах
пробой происходит при больших
напряжениях, чем в случае постоянного
или длительного приложения переменного
напряжения. Продолжительное воздействие
электрического поля высокой напряженности
приводит к необратимым процессам в
диэлектрике, в результате которых его
пробивное напряжение снижается т.е.
происходит его электрическое старение.
Вследствие такого старения срок службы
изоляции ограничен.
Источник