Растяжения пружины формула через
Определение и формула жесткости пружины
Определение
Силу, которая возникает в результате деформации тела и пытающаяся вернуть его в исходное состояние, называют силой упругости.
Чаще всего ее обозначают ${overline{F}}_{upr}$. Сила упругости появляется только при деформации тела и исчезает, если пропадает деформация. Если после снятия внешней нагрузки тело восстанавливает свои размеры и форму полностью, то такая деформация называется упругой.
Современник И. Ньютона Р. Гук установил зависимость силы упругости от величины деформации. Гук долго сомневался в справедливости своих выводов. В одной из своих книг он привел зашифрованную формулировку своего закона. Которая означала: «Ut tensio, sic vis» в переводе с латыни: каково растяжение, такова сила.
Рассмотрим пружину, на которую действует растягивающая сила ($overline{F}$), которая направлена вертикально вниз (рис.1).
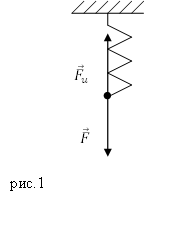
Силу $overline{F }$ назовем деформирующей силой. От воздействия деформирующей силы длина пружины увеличивается. В результате в пружине появляется сила упругости (${overline{F}}_u$), уравновешивающая силу $overline{F }$. Если деформация является небольшой и упругой, то удлинение пружины ($Delta l$) прямо пропорционально деформирующей силе:
[overline{F}=kDelta lleft(1right),]
где в коэффициент пропорциональности называется жесткостью пружины (коэффициентом упругости) $k$.
Жесткость (как свойство) — это характеристика упругих свойств тела, которое деформируют. Жесткость считают возможностью тела оказать противодействие внешней силе, способность сохранять свои геометрические параметры. Чем больше жесткость пружины, тем меньше она изменяет свою длину под воздействием заданной силы. Коэффициент жесткости — это основная характеристика жесткости (как свойства тела).
Коэффициент жесткости пружины зависит от материала, из которого сделана пружина и ее геометрических характеристик. Например, коэффициент жесткости витой цилиндрической пружины, которая намотана из проволоки круглого сечения, подвергаемая упругой деформации вдоль своей оси может быть вычислена как:
[k=frac{Gd^4}{8d^3_pn}left(2right),]
где $G$ — модуль сдвига (величина, зависящая от материала); $d$ — диаметр проволоки; $d_p$ — диаметр витка пружины; $n$ — количество витков пружины.
Единицей измерения коэффициента жесткости в Международной системе единиц (Си) является ньютон, деленный на метр:
[left[kright]=left[frac{F_{upr }}{x}right]=frac{left[F_{upr }right]}{left[xright]}=frac{Н}{м}.]
Коэффициент жесткости равен величине силы, которую следует приложить к пружине для изменения ее длины на единицу расстояния.
Формула жесткости соединений пружин
Пусть $N$ пружин соединены последовательно. Тогда жесткость всего соединения равна:
[frac{1}{k}=frac{1}{k_1}+frac{1}{k_2}+dots =sumlimits^N_{ i=1}{frac{1}{k_i}left(3right),}]
где $k_i$ — жесткость $i-ой$ пружины.
При последовательном соединении пружин жесткость системы определяют как:
[k=k_1+k_2+dots +sumlimits^N_{i=1}{k_i}left(4right).]
Примеры задач с решением
Пример 1
Задание. Пружина в отсутствии нагрузки имеет длину $l=0,01$ м и жесткость равную 10 $frac{Н}{м}. $Чему будет равна жесткость пружины и ее длина, если на пружину действовать силой $F$= 2 Н? Считайте деформацию пружины малой и упругой.
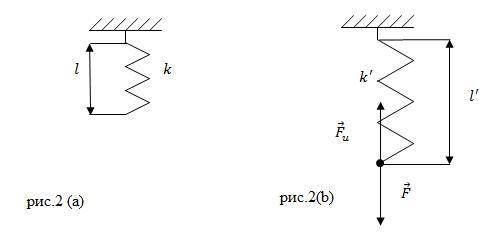
Решение. Жесткость пружины при упругих деформациях является постоянной величиной, значит, в нашей задаче:
[k=k’left(1.1right).]
При упругих деформациях выполняется закон Гука:
[F=kDelta l left(1.2right).]
Из (1.2) найдем удлинение пружины:
[Delta l=frac{F}{k}left(1.3right).]
Длина растянутой пружины равна:
[l’=l+Delta l=l+frac{F}{k}.]
Вычислим новую длину пружины:
[l’=0,01+frac{2}{10}=0,21 left(мright).]
Ответ. 1) $k’=10 frac{Н}{м}$; 2) $l’=0,21$ м
Пример 2
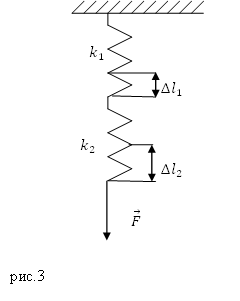
Задание. Две пружины, имеющие жесткости $k_1$ и $k_2$ соединили последовательно. Какой будет удлинение первой пружины (рис.3), если длина второй пружины увеличилась на величину $Delta l_2$?

Решение. Если пружины соединены последовательно, то деформирующая сила ($overline{F}$), действующая на каждую из пружин одинакова, то есть можно записать для первой пружины:
[F=k_1Delta l_1left(2.1right).]
Для второй пружины запишем:
[F=k_2Delta l_2left(2.2right).]
Если равны левые части выражений (2.1) и (2.2), то можно приравнять и правые части:
[k_1Delta l_1=k_2Delta l_2left(2.3right).]
Из равенства (2.3) получим удлинение первой пружины:
[Delta l_1=frac{k_2Delta l_2}{k_1}.]
Ответ. $Delta l_1=frac{k_2Delta l_2}{k_1}$
Читать дальше: формула закона Архимеда.
Источник
Определение 1
Пружина — упругий объект, целенаправленно подвергающийся сжатию или растяжению, в результате чего может запасать энергию, а затем, при ослабевании внешней деформирующей силы, возвращать ее. Пружины в нормальных условиях не должны подвергаться остаточным (пластическим) деформациям, т.е. таким воздействиям, после которых форма изделия уже не восстанавливается вследствие нарушения структуры их материала.
Типы пружин
Пружины можно классифицировать по направлению прилагаемой нагрузки:
- пружины растяжения; предназначены для работы в режиме растягивания, при деформации их длина увеличивается; как правило, такие устройства имеют нулевой шаг, т.е. намотаны «виток к витку»; примером могут служить пружины в весах-безменах, пружины для автоматического закрытия дверей и т.д.;
- пружины сжатия под нагрузкой, напротив, укорачиваются; в исходном состоянии между их витками есть некоторое расстояние, как, например, в амортизаторах автомобильных подвесок.
В данной статье рассматриваются пружины, представляющие собой цилиндрические спирали. В технике применяется много других разновидностей упругих устройств: пружины в виде плоских спиралей (используются в механических часах), в виде полос (рессоры), пружины кручения (в точных весах), тарельчатые (сжимающиеся конические поверхности) и т.п. Своего рода пружинами являются амортизирующие изделия из полимерных эластичных материалов, прежде всего резины. Во всех этих устройствах используется один и тот же принцип — запасать энергию упругой деформации и возвращать ее.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Физические характеристики пружин
Цилиндрические пружины характеризуются рядом параметров, сочетание которых обуславливает их жесткость — способность сопротивляться деформации:
- материал; пружины чаще всего изготавливают из стальной проволоки, причем сталь в них применялася особая, ее характеризует среднее или высокое содержание углерода, низкое содержание других примесей (низколегированный сплав) и особая термообработка (закалка), придающая материалу дополнительную упругость;
- диаметр проволоки; чем он меньше, тем эластичнее пружина, но тем меньше ее способность запасать энергию; пружины сжатия изготавливают, как правило, из более толстой проволоки, чем пружины растяжения;
- форма сечения проволоки; не всегда проволока, из которой намотана пружина, имеет круглое сечение; уплощенное сечение имеют пружины сжатия, чтобы при максимальном сокращении длины (виток «садится» на соседний виток) конструкция была более устойчивой;
- длина и диаметр пружины; длину пружины следует отличать от длины проволоки, из которой она намотана; эти два параметра согласуются через количество витков и диаметр пружины, который, в свою очередь, не следует путать с диаметром проволоки.
Существуют и другие физические характеристики, влияющие на работоспособность пружин. Например, при повышении температуры металл становится менее упругим, а при существенном ее понижении может стать хрупким. При интенсивной эксплуатации пружина со временем теряет часть упругости по причине постепенного разрушения связей между атомами кристаллической решетки.
Понятие жесткости
Определение 2
Жесткость как физическая величина характеризует силу, которую нужно приложить к пружине для достижения определенной степени растяжения или сжатия.
Коэффициент жесткости рассчитывается по формуле Гука:
$F = -k cdot x$,
где $F$ — сила, развиваемая пружиной, $k$ — коэффициент жесткости, зависящий от ее характеристик (см. выше) и измеряемый в ньютонах на метр, $x$ — абсолютное приращение расстояния, на которое изменилась длина пружины после приложения внешней силы. Знак минус в правой части формулы свидетельствует о том, что сила, порождаемая пружиной, действует в противоположном по отношению к нагрузке направлении.
Коэффициент жесткости можно вычислить экспериментально, подвешивая на расположенную вертикально и закрепленную за верхний конец пружину грузы с известной массой. В этом случае имеет место зависимость
$m cdot g — k cdot x = 0$,
где $m$ — масса, $g$ — ускорение свободного падения. Отсюда
$k = frac{m cdot g}{x}$
Расчет жесткости цилиндрической пружины
Довольно просто понять как работает плоская пружина. Если положить на край письменного стола линейку и прижать один ее конец рукой к поверхности, но второй можно упруго изгибать, запасая и высвобождая энергию. Очевидно, что в момент изгиба расстояния между молекулами материала в некоторых фрагментах линейки увеличиваются, в некоторых уменьшаются. Электромагнитные связи, действующие между молекулами, стремятся вернуть вещество к прежнему геометрическому состоянию.
Несколько сложнее дело обстоит с цилиндрической пружиной. В ней энергия запасается не благодаря деформации изгиба, а за счет скручивания проволоки, из которой пружина навита, относительно продольной оси этой проволоки.
Представим сильно увеличенное сечение проволоки, из которой навита цилиндрическая пружина, выполненное перпендикулярной ее оси плоскостью. При таком рассмотрении можно абстрагироваться от спиральной формы и мысленно разбить весь объем проволоки на множество соприкасающихся торцевыми поверхностями «цилиндров», диаметр которых равен диаметру проволоки, а высота стремится к нулю. Между соприкасающимися торцами действуют молекулярные силы, препятствующие деформации.
При растяжении или сжатии пружины угол наклона между витками изменяется. Соседние «цилиндры» при этом вращаются друг относительно друга в противоположных направлениях вокруг общей оси. В каждом таком сечении запасается энергия. Отсюда следует, что чем из более длинного куска проволоки навита пружина (здесь играют роль диаметр и высота цилиндра, а также шаг витка), тем большее количество энергии она способна запасти. Увеличение диаметра проволоки также повышает ее энергоемкость. В целом формула, учитывающая основные факторы жесткости пружины, выглядит так:
$k = frac{r^4}{4R^3} cdot frac{G}{n}$,
где:
- $R$ — радиус цилиндра пружины,
- $n$ — количество витков проволоки радиуса $r$,
- $G$ — коэффициент, зависящий от материала.
Пример 1
Рассчитать коэффициент жесткости пружины, выполненной из стальной проволоки с $G = 8 cdot 10^{10}$ Па и диаметром 1 мм. Радиус пружины 20 мм, количество витков — 25.
Подставим в формулу числовые значения, попутно переведя их в единицы системы СИ:
$k = frac{(10^{-3})^4}{4 cdot (2 cdot 10^{-2})^3} cdot frac{8 cdot 10^{10}}{25} = frac{8 cdot 10^{-2}}{10^2 cdot 2^3 cdot 10^{-6}} = 100$
Ответ: $100 frac{Н}{м}$
Источник
При колебаниях пружины восстанавливающая сила обусловлена ее упругостью. В определенных пределах, согласно закону Гука, вызванная деформацией сила пропорциональна величине деформации.
Поэтому упругие колебания являются гармоническими. В случае пружин величина жесткости обычно обозначается через k и именуется коэффициентом упругости пружины.
| k | коэффициент упругости пружины, | Ньютон / метр |
|---|---|---|
| F | сила, вызывающая деформацию Δl, | Ньютон |
| Δl | удлинение, прогиб или другое изменение формы, | метр |
| ω | угловая частота, | радиан / секунда |
| f | линейная частота, | Герц |
| T | период, длительность полного колебания, | секунда |
| m | масса колебательной системы, обычно тела, укрепленного на пружине, | кг |
И в соответствии с (9)
Масса самой пружины в (3, 4, 5) не учитывается. При точных расчетах массу m следует увеличить приблизительно на mпр/ 3 ( mпр — масса пружины).
Величины ω, f и T не зависят от амплитуды.
Для определения устойчивости и сопротивления к внешним нагрузкам используется такой параметр, как жесткость пружины. Также он называется коэффициентом Гука или упругости. По сути, характеристика жесткости пружины определяет степень ее надежности и зависит от используемого материала при производстве.
Измерению коэффициента жесткости подлежат следующие типы пружин:
Изготовление пружин любого типа вы можете заказать здесь.
Какую жесткость имеет пружина
При выборе готовых пружин, например для подвески автомобиля, определить, какую жесткость она имеет, можно по коду продукта либо по маркировке, которая наносится краской. В остальных случаях расчет жесткости производится исключительно экспериментальными методами.
Жесткость пружины по отношению к деформации бывает величиной переменной или постоянной. Изделия, жесткость которых при деформации остается неизменной называются линейными. А те, у которых есть зависимость коэффициента жесткости от изменения положения витков, получили название «прогрессивные».
В автомобилестроении в отношении подвески существует следующая классификация жесткости пружин:
- Возрастающая (прогрессирующая). Характерна для более жесткого хода автомобиля.
- Уменьшающаяся (регрессирующая) жесткость. Напротив, обеспечивает, «мягкость» подвески.
Определение величины жесткости зависит от следующих исходных данных:
- Тип сырья, используемый при изготовлении;
- Диаметр витков металлической проволоки (Dw);
- Диаметр пружины (в расчет берется средняя величина) (Dm);
- Число витков пружины (Na).
Как рассчитать жесткость пружины
Для расчета коэффициента жесткости применяется формула:
k = G * (Dw)^4 / 8 * Na * (Dm)^3,
где G – модуль сдвига. Данную величину можно не рассчитывать, так как она приведена в таблицах к различным материалам. Например, для обыкновенной стали она равна 80 ГПа, для пружинной – 78,5 ГПа. Из формулы понятно, что наибольшее влияние на коэффициент жесткости пружины оказывают оставшиеся три величины: диаметр и число витков, а также диаметр самой пружины. Для достижения необходимых показателей жесткости изменению подлежат именно эти характеристики.
Вычислить коэффициент жесткости экспериментальным путем можно при помощи простейших инструментов: самой пружины, линейки и груза, который будет воздействовать на опытный образец.
Определение коэффициента жесткости растяжения
Для определения коэффициента жесткости растяжения производятся следующие расчеты.
- Измеряется длина пружины в вертикальном подвесе с одной свободной стороной изделия – L1;
- Измеряется длина пружины с подвешенным грузом – L2.Если взять груз массой 100гр., то он будет воздействовать силой в 1Н (Ньютон) – величина F;
- Вычисляется разница между последним и первым показателем длины – L;
- Рассчитывается коэффициент упругости по формуле: k = F/L.
Определение коэффициента жесткости сжатия производится по этой же формуле. Только вместо подвешивания груз устанавливается на верхнюю часть вертикально установленной пружины.
Подводя итог, делаем вывод, что показатель жесткости пружины является одной из существенных характеристик изделия, которая указывает на качество исходного материала и определяет долговечность использования конечного изделия.
Формулы и способы расчета пружин из стали круглого сечения по ГОСТ 13765
Пружина сжатия Пружина растяжения
| Наименование параметра | Обозначение | Расчетные формулы и значения |
|---|---|---|
| Сила пружины при предварительной деформации, Н | F 1 | Принимается в зависимости от нагрузки пружины |
| Сила пружины при рабочей деформации (соответствует наибольшему принудительному перемещению подвижного звена в механизме), Н | F 3 | Принимается в зависимости от нагрузки пружины |
| Рабочий ход пружины, мм | h | Принимается в зависимости от нагрузки пружины |
| Наибольшая скорость перемещения подвижного конца пружины при нагружении или разгрузке, м/с | v max | Принимается в зависимости от нагрузки пружины |
| Выносливость пружины, число циклов до разрушения | N F | Принимается в зависимости от нагрузки пружины |
| Наружный диаметр пружины, мм | D 1 | Предварительно принимаются с учетом конструкции узла. Уточняются по таблицам ГОСТ 13766…ГОСТ 13776 |
| Относительный инерционный зазор пружины сжатия. Для пружин растяжения служит ограничением максимальной деформации | δ | δ = 1 — F 2 / F 3 (1) Для пружин сжатия классов I и II δ = 0,05 — 0,25 для пружин растяжения δ = 0,05 — 0,10 для одножильных пружин класса III δ = 0,10 — 0,40 для трехжильных класса III δ = 0,15 — 0,40 |
| Сила пружины при максимальной деформации, Н | F 3 |
Уточняется по таблицам ГОСТ 13766 ÷ ГОСТ 13776
s» (при F > 0)
Для трехжильных пружин
Для трехжильных пружин
G = 7,85 х 10 4
где g — ускорение свободного падения, м/с 2
γ — удельный вес, Н/м 3
Для пружинной стали ρ = 8•10 3
Для пружин с предварительным напряжением
Для трехжильных пружин
где n2 — число опорных витков
Для трехжильных пружин
Для трехжильных пружин
Рекомендуется назначать от 4 до 12
| i | 4,0 | 4,5 | 5,0 | 5,5 | 6,0 | 7,0 и более |
| Δ | 1,029 | 1,021 | 1,015 | 1,010 | 1,005 | 1,000 |
где n3 — число обработанных витков
Для трехжильных пружин
Для пружин растяжения с зацепами
Для пружин растяжения
Для пружин растяжения
Для трехжильных пружин
Для пружин растяжения
Для трехжильных пружин
Для пружин растяжения с предварительным напряжением
Методика определения размеров пружин
Исходными величинами для определения размеров пружин являются силы F 1 и F 2, рабочий ход h, наибольшая скорость перемещения подвижного конца пружины при нагружении или при разгрузке v max, выносливость N F и наружный диаметр пружины D 1 (предварительный).
Если задана только одна сила F2 , то вместо рабочего хода h для подсчета берут величину рабочей деформации s 2, соответствующую заданной силе
По величине заданной выносливости NF предварительно определяют принадлежность пружины к соответствующему классу
По заданной силе F 2 и крайним значениям инерционного зазора δ вычисляют по формуле (2) значение силы F 3
По значению F 3, пользуясь таблицей, предварительно определяют разряд пружины
По таблицам «Параметры пружин» находят строку, в которой наружный диаметр витка пружины наиболее близок к предварительно заданному значению D 1. В этой же строке находят соответствующие значения силы F 3 и диаметра проволоки d
Для пружин из закаливаемых марок сталей максимальное касательное напряжение τ 3 находят по таблице, для пружин из холоднотянутой и термообработанной проволоки τ 3 вычисляют с учетом значений временного сопротивления Rm . Для холоднотянутой проволоки Rm определяют из ГОСТ 9389, для термообработанной — из ГОСТ 1071
По полученным значениям F 3 и τ 3, а также по заданному значению F 2 по формулам (5) и (5а) вычисляют критическую скорость vK и отношение vmax / vK , подтверждающее или отрицающее принадлежность пружины к предварительно установленному классу.
При несоблюдении условий vmax / vK < 1 пружины I и II классов относят к последующему классу или повторяют расчеты, изменив исходные условия. Если невозможно изменение исходных условий, работоспособность обеспечивается комплектом запасных пружин
По окончательно установленному классу и разряду в соответствующей таблице на параметры витков пружин, помимо ранее найденных величин F3, D1 и d, находят величины c1 и s3 , после чего остальные размеры пружины и габариты узла вычисляют по формулам (6)-(25)
Источник
