Растяжение вдоль оси ординат

3.1 Сжатие (растяжение) графика вдоль оси ординат
Рассмотрим
функцию вида y=A![]() ,
,
где A>0.
Нетрудно заметить, что при равных
значениях аргумента ординаты графика
этой функции будут в A
раз больше ординат графика функции
y=f(x)
при A>1
или в
![]() раз меньше ординат графика функцииy=f(x)
раз меньше ординат графика функцииy=f(x)
при A<1.
Таким образом, получаем следующее
правило.
Для
построения графика функции y=A![]()
следует построить график функции y=f(x)
и увеличить его ординаты в A
раз при A>1
(произвести растяжение графика вдоль
оси ординат) или уменьшить его ординаты
в
![]() раз приA<1
раз приA<1
(произвести сжатие графика вдоль оси
ординат). Полученный график является
графиком функции y=A![]() .
.
Пример
13. Построить
график функции y=2cos
x.
Р
е ш е н и е: Строим график функции y=cos
x
(рис.16 – пунктирная кривая) и растяжением
этого графика вдоль оси ординат в 2
раза получаем график функции y=2cos
x
(сплошная кривая).
Пример
14. Построить
график функции y=![]() x2.
x2.
Р
е ш е н и е: Строим график функции y=x2
и сжатием этого графика в 3 раза вдоль
оси ординат получаем график функции
y=![]() x2
x2
(рис.17).
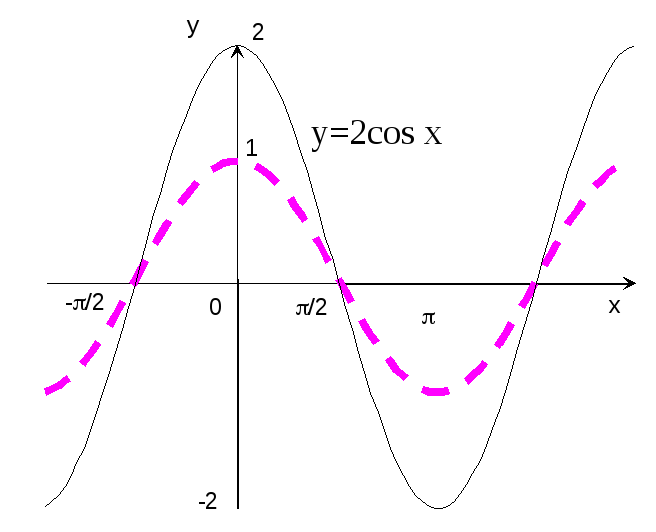
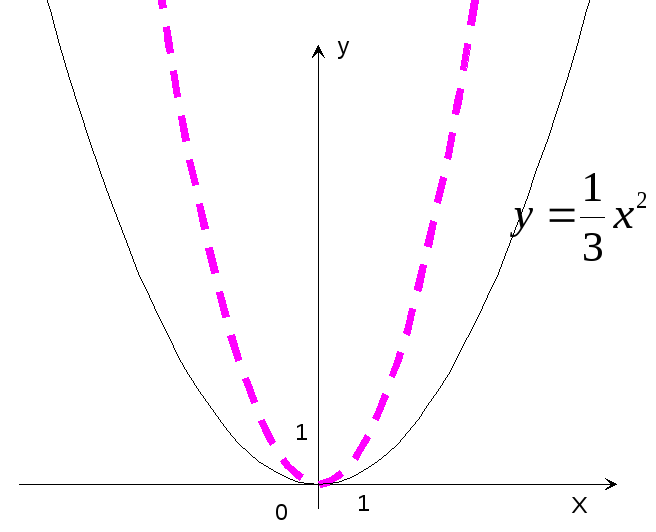
Рис.16
Рис.17
3.2. Сжатие (растяжение) графика вдоль оси абсцисс
Пусть
требуется построить график функции
y=f(x),
где >0.
Рассмотрим функцию y=f(x),
которая в произвольной точке x=x1
принимает значение y1=f(x1).
Очевидно,
что функция y=f(x)
принимает такое же значение в точке
x=x2,
координата
к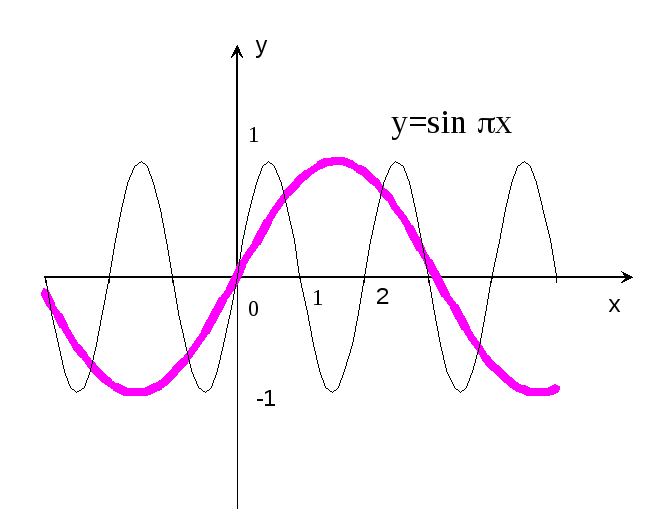 оторой
оторой
определяется равенствомx1=x2,
или x2=![]() ,
,
причём это равенство справедливо для
совокупности всех значений x
из области определения функции.
Следовательно, график функции y=f(x)
оказывается сжатым (при >1)
или растянутым (при <1)
вдоль оси абсцисс относительно графика
функции y=f(x).
Таким образом, получаем следующее
правило.
Для
построения графика функции y=f(x)
следует построить график функции y=f(x)
и уменьшить его абсциссы в
раз при >1
(произвести сжатие графика вдоль оси
абсцисс) или увеличить его абсциссы в
![]() раз при<1
раз при<1
(произвести растяжение графика вдоль
оси абсцисс). Полученный график является
графиком функции y=f(x).
П
Рис. 18
ример 15.Построить
график функции
![]() x.
x.
Р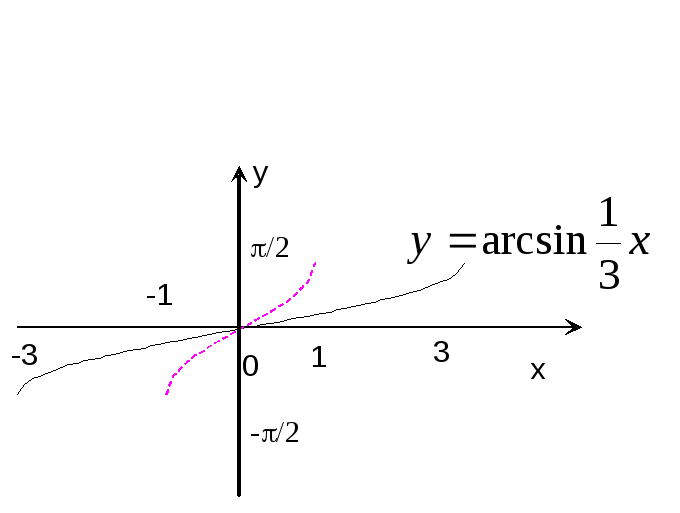 е ш е н и е: Строим график функции
е ш е н и е: Строим график функции
![]() x
x
(рис.18 – пунктирная кривая), и проводя
его сжатие в
раз вдоль оси абсцисс, получаем график
функции
![]() x
x
(сплошная кривая). Период этой функции
уже равен не 2,
а
![]() =2.
=2.
График пересекает ось абсцисс в точкахx=0,![]() …
…
.
Пример
16. Построить
график функции
![]() .
.
Р
е ш е н и е: Строим график функции
![]() и, растянув его вдоль оси абсцисс в 3
и, растянув его вдоль оси абсцисс в 3
раза, получаем график функции![]() .
.
4. Комбинация переноса, отражения и деформации
Рис.
19
Очень часто при построении графиков
функций применяют композицию приёмов,
изложенных в пунктах 1-3. Последовательное
применение ряда таких приёмов позволяет
существенно упростить построение
графика исходной функции и нередко
свести его в конце концов к построению
одной из простейших элементарных
функций.
Рассмотрим,
как с учётом изложенного следует,
например, построить
график функции вида y=Af(x+a)+b.
Запишем
исходную функцию в виде y=Af
[
( x+![]()
) ] +b
и схему поэтапного её упрощения
(последовательность преобразований):
1
 .y=Af
.y=Af
[
( x+![]()
) ] + b
; перенос оси абсцисс на b
единиц;
2
 .y=Af
.y=Af
[
( x+![]()
) ]; перенос оси ординат на
![]()
единиц;
3. y=Af
[
x
]; отражение графика относительно оси
абсцисс
( этап
этап
выполняется только приA<0);
4 .y=A·
.y=A·
f
(x); сжатие
или растяжение графика
вдоль оси ординат;
5. y=f
(x) отражение
графика относительно оси ординат
(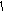 этап
этап
выполняется только при<0);
6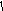 .y=f
.y=f
(
x); сжатие
или растяжение вдоль оси абсцисс;
7. y=f
( x);
Проводя
построение графика шаг за шагом в
порядке, обратном порядку упрощения
вида функции с учётом всех указанных
правил, получим график исходной функции.
Пример 17. Построить
график функции y=![]() .
.
Р
 е ш е н и е: Схема построения графика :
е ш е н и е: Схема построения графика :
y
 =
=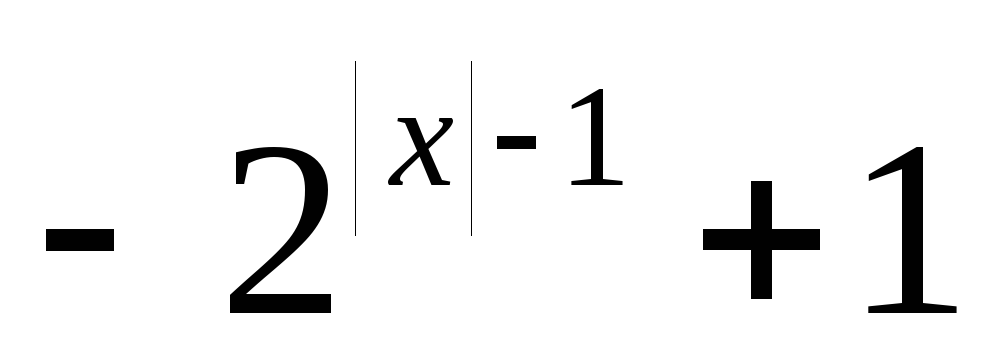
x
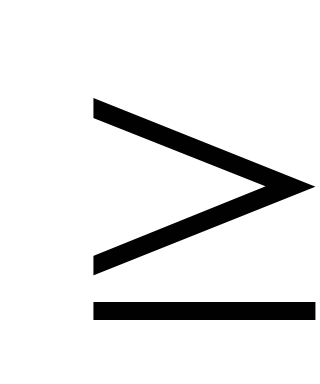 0,
0,
y=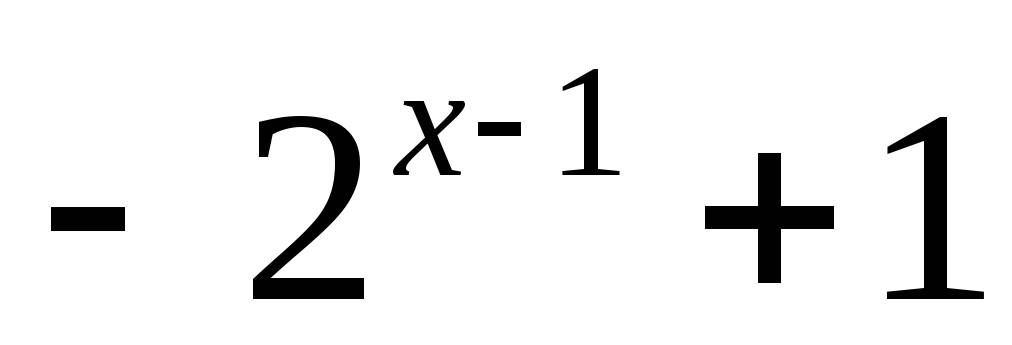 ;
;y=
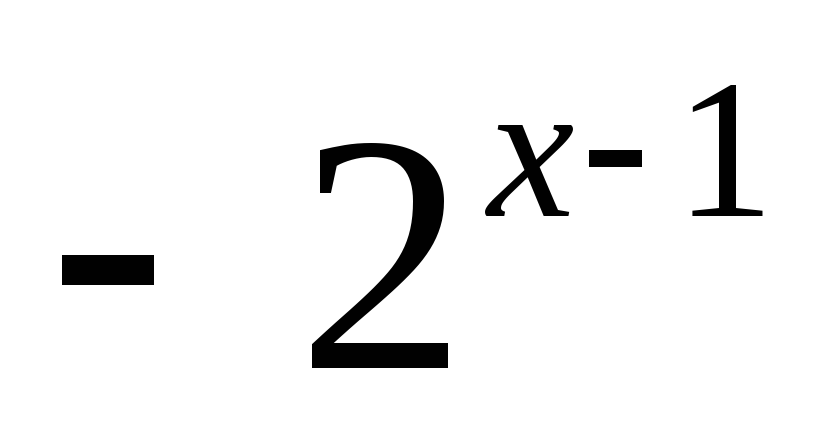 ;
;у=
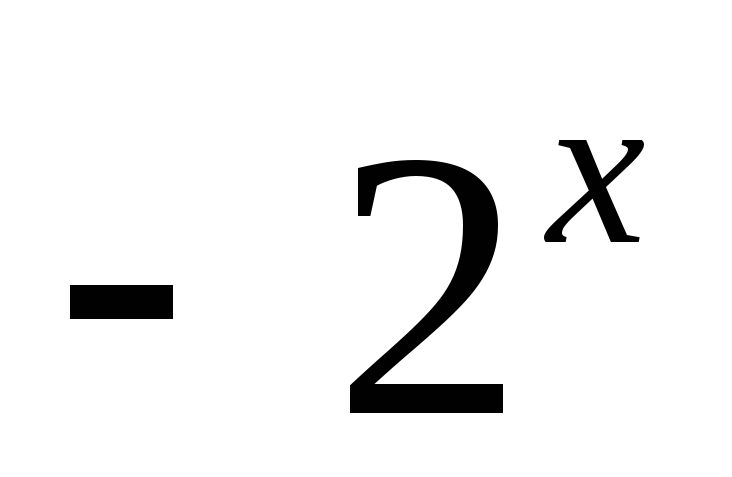 ;
;y=
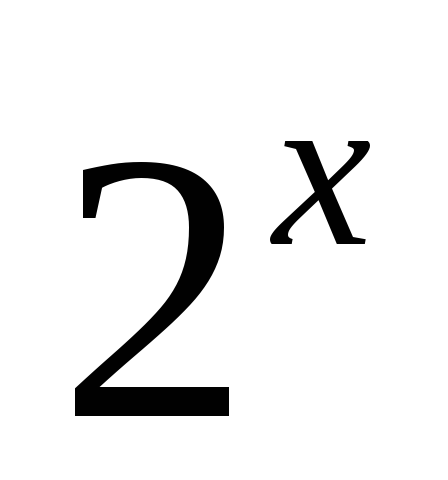 ;
;
Итак,
построение графика исходной функции
следует начинать с построения графика
функции y=![]() .
.
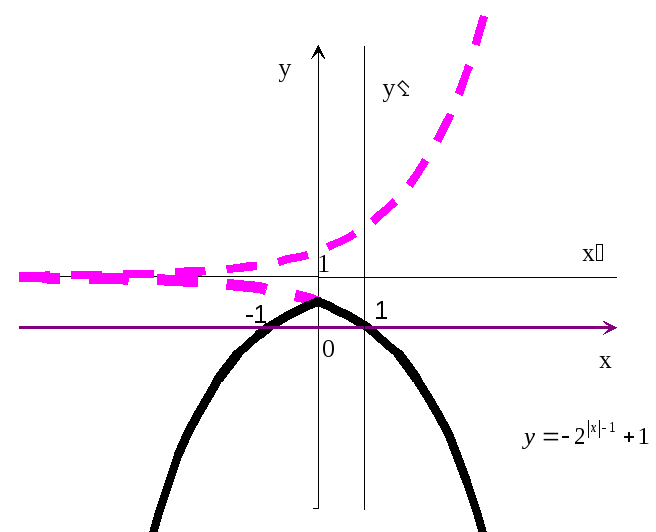
График (рис.20) пересекает ось ординат
в точке![]() (из условияx=0),
(из условияx=0),
а ось абсцисс в точках x=1
(из условия y=0,
т.е.![]() =0).
=0).
 В
В
заключении отметим, что порядок упрощения
целесообразно проводить в следующей
последовательности.
Использование
чётности или нечётности функции.Перенос осей.
Отражение и
деформация.
Построение
же графика, как обычно, выполняется в
обратной последовательности.
Рис.20
Задание для
самостоятельного выполнения
Ниже
приводятся тексты заданий для
самостоятельного выполнения. Вам
необходимо построить графики функций,
оформить работу отдельно от решений по
другим предметам и выслать в адрес
Хабаровской краевой заочной
физико-математической школы.
М.11.2.1 С
помощью элементарных преобразований
постройте графики следующих функций:
y=x2-2;
y=(x+1)2;
y=sin
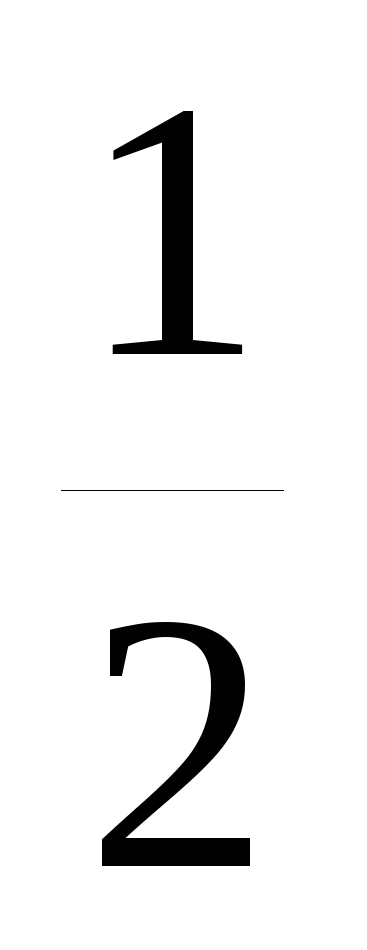 x;
x;y=-
3sin x;y=tg
 ;
;
М.11.2.2.
Написать последовательность преобразований
и построить графики следующих функций:
y=
 ;
;y=(x-1)3+2;
y=ln
(1-x);y=tg(-
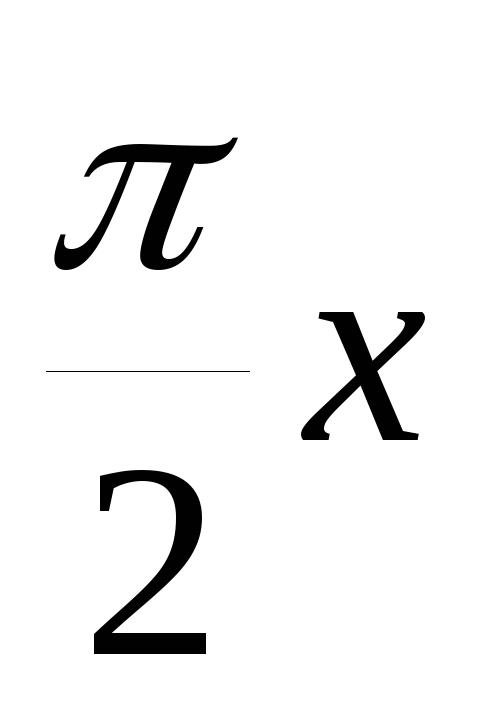 );
);y=
 cos(2x-1)-2.
cos(2x-1)-2.
Хабаровская краевая заочная
физико-математическая школа
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Преобразования графиков: параллельный перенос, симметрия
В чистом виде основные элементарные функции встречаются, к сожалению, не так часто. Гораздо чаще приходится иметь дело с элементарными функциями, полученными из основных элементарных при помощи добавления констант и коэффициентов. Графики таких функций можно строить, применяя геометрические преобразования к графикам соответствующих основных элементарных функций (или переходить к новой системе координат).
С помощью геометрических преобразований графика функции f(x) может быть построен график любой функции вида ( pm {k_1} cdot f( pm {k_2} cdot (x + a)) + b,) где ({k_1},{k_2} > 0) — коэффициенты сжатия или растяжения (в зависимости от их значений) вдоль осей oy и ox соответственно. Знаки «минус» перед коэффициентами указывают на симметричное отображение графика относительно координатных осей, а и b определяют сдвиг относительно осей абсцисс и ординат соответственно.
Таким образом, различают три вида геометрических преобразований графика функции:
1. Первый вид — масштабирование (сжатие или растяжение) вдоль осей абсцисс и ординат.
На необходимость масштабирования указывают коэффициенты k1 и k2, отличные от единицы, если (0 < {k_1} < 1,0 < {k_2} < 1) , то происходит сжатие графика относительно oy и растяжение относительно ox , если ({k_1},{k_2} > 1) , то производим растяжение вдоль оси ординат и сжатие вдоль оси абсцисс.
2. Второй вид — симметричное (зеркальное) отображение относительно координатных осей.
На необходимость этого преобразования указывают знаки «минус» перед коэффициентами k1 (в этом случае симметрично отображаем график относительно оси ox ) и k2 (в этом случае симметрично отображаем график относительно оси oy). Если знаков «минус» нет, то этот шаг пропускается.
3. Третий вид — параллельный перенос (сдвиг) вдоль осей ox и oy.
Это преобразование производится в последнюю очередь при наличии коэффициентов a и b, отличных от нуля. При положительном а график сдвигается влево на |а| единиц, при отрицательных а — вправо на |а| единиц. При положительном b график функции параллельно переносим вверх на |b| единиц, при отрицательном b — вниз на |b| единиц.
Рассмотрим примеры
Пример1
Построить графики функции (y = {x^2} — 10) и (y = {x^2} + 10) в одной координатной плоскости.
Построим для начала график функции (y = {x^2}) , это парабола с вершиной в точке (0;0) и ветвями вверх.
Для построения искомого графика функции (y = {x^2} — 10) необходимо параболу параллельно перенести в отрицательном направлении по У, т.е. вниз. Для построения искомого графика функции (y = {x^2} + 10) необходимо параболу параллельно перенести в положительном направлении по У, т.е. вверх.
Пример2
Построить графики функций (y = {left( {x + 2} right)^2}) и (y = {left( {x — 2} right)^2}) .
За основу возьмем тот же график параболы, но параллельный перенос будем осуществлять вдоль оси Ох. По правилу переноса график сдвинется влево на 2 единицы для функции (y = {left( {x + 2} right)^2}) . А для функции (y = {left( {x — 2} right)^2}) сдвиг произойдет вправо.
Пример3
Построить график функции (y = — {x^2}) .
За основу возьмем тот же график параболы. Производимое изменение графика носит название -отображение. Картинка получится симметричной исходной параболе, симметрия относительно Ох.
Пример4
Построить графики функций (y = left( {3{x^2}} right)) и (y = left( {frac{1}{3}{x^2}} right)) .
Для построения этих графиков произведем сжатие графика (y = {x^2}) для первой функции и растяжение – для второй.
Источник
Анна Малкова
В этой статье мы расскажем об основных преобразованиях графиков функций. Что нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали. Как задать растяжение графика по горизонтали или вертикали. Как отразить график относительно оси Х или Y.
Очень жаль, что эта тема — полезная и очень интересная — выпадает из школьной программы. На нее не постоянно хватает времени. Из-за этого многим старшеклассникам не даются задачи с параметрами — которые на самом деле похожи на конструктор, где вы собираете решение из знакомых элементов. Хотя бы для того, чтобы решать задачи с параметрами, стоит научиться строить графики функций.
Но конечно, не только для того, чтобы сдать ЕГЭ. Первая лекция на первом курсе технического или экономического вуза посвящена функциям и графикам. Первые зачеты в курсе матанализа связаны с функциями и графиками.
Начнем со сдвигов графиков по Х и по Y.
Сдвиг по горизонтали.
Пусть функция задана формулой и Тогда график функции сдвинут относительно исходной на а вправо. График функции сдвинут относительно исходной на а влево.

1. Сдвиг по вертикали.
Пусть функция задана формулой и С — некоторое положительное число. Тогда график функции сдвинут относительно исходного на С вверх. График функции сдвинут относительно исходного на С вниз.

Теперь растяжение графика. Или сжатие.
2. Растяжение (сжатие) по горизонтали.
Пусть функция задана формулой и Тогда график функции растянут относительно исходного в k раз по горизонтали, если , и сжат относительно исходного в k раз по горизонтали, если

3. Растяжение (сжатие) по вертикали
Пусть функция задана формулой и Тогда график функции растянут относительно исходного в М раз по вертикали, если , и сжат относительно исходного в М раз по вертикали, если

И отражение по горизонтали.
4. Отражение по горизонтали
График функции симметричен графику функции относительно оси Y.


5. Отражение по вертикали.
График функции симметричен графику функции относительно оси Х.

Друзья, не возникло ли у вас ощущения, что вы все это где-то видели? Да, наверняка видели, если когда-либо редактировали изображения в графическом редакторе на компьютере. Изображение можно сдвинуть (по горизонтали или вертикали). Растянуть (по горизонтали или вертикали). Отразить. И все это мы делаем с графиками функций.
И еще два интересных преобразования. Здесь в формулах присутствует знак модуля. Если не помните, что такое модуль, — срочно повторите эту тему.
6. Графики функций и
На рисунке изображен график функции Она специально взята такая — несимметричная относительно нуля.

Построим график функции
Конечно же, мы пользуемся определением модуля.
Это мы и видим на графике. Для неотрицательных значений х график остался таким же, как был. А вместо каждого отрицательного х мы взяли противоположное ему положительное число. И поэтому вся та часть графика функции, что лежала слева от оси Х, заменилась на зеркально отраженную правую часть графика.

Теперь график функции Вы уже догадались, что будет. Вся часть графика, лежащая ниже оси Х, зеркально отражается в верхнюю полуплоскость. А верхняя часть графика, лежащая выше оси Х, остается на месте.

Как определить по формуле функции, будет график преобразован по горизонтали (по Х) или по вертикали (по Y)? Разница очевидна. Если сначала мы что-либо делаем с аргументом х (прибавляем к нему какое-либо число, умножаем на какое-либо число или берем модуль) — преобразование по Х. Если сначала мы нашли функцию, а затем уже к значению функции что-то прибавили, или на какое-нибудь число умножили, или взяли модуль, — преобразование по Y.
Вот самые простые задачи на преобразование графиков.
1. Построим график функции
Это квадратичная парабола, сдвинутая на 3 влево по x и на 1 вниз по y.
Вершина в точке

2. Построим график функции
Выделим полный квадрат в формуле.
График — квадратичная парабола, сдвинутая на 2 вправо по x и на 5 вниз по y.
Обратите внимание: график функции пересекает ось y в точке На нашем графике это точка

Продолжение — в статье «Построение графиков функций».
Источник
Автор/ы проекта (ФИО)
Холева Ольга Вячеславовна
Должность (с указанием преподаваемого предмета)
учитель математики
Образовательное учреждение
МОУ СОШ №73 им.А.Ф.Чернонога г.Воронеж
Название проекта
«Преобразования графиков функций»
Операционная система, с помощью которой подготовлен мультимедийный компонент (Windows, Linux)
Windows
Форма (презентация, тест и т.п.)
презентация
Размер ресурса (мегабайт)
0,95Мб
Технические данные
(компьютер, интерактивная доска и другие.)
Компьютер, проектор, экран
Учебный предмет
Алгебра
Класс
9-10-11
Название учебного пособия и образовательной программы с указанием авторов, к которому относится ресурс
Программа основного общего образования
Учебники:
А.Н.Колмогоров и др. «Алгебра и начала анализа 10-11»
А.Г.Мордкович «Алгебра 8»
А.Г.Мордкович «Алгебра 9»
А.Г.Мордкович «Алгебра и начала анализа 10-11»
Ю.Н.Макарычев и др. «Алгебра 9»
Ю.Н.Макарычев и др. «Алгебра 9 с углубленным изучением математики»
Название темы или раздела учебного курса
Функции и их графики
Формат ресурса — основного файла (ppt, avi, exe, doc или другие)
ppt
Вид ресурса
(презентация, видео, текстовый документ, электронная таблица и другие)
презентация
Образовательный тип
(Поясняющий текст, учебный текст, методичка, разработанная программа, электронный тест, электронный учебник и другие)
учебный текст в виде презентации c графической информацией с анимационными эффектами
Средства Microsoft Office или другое ПО, с помощью которых создан дидактический материал
Microsoft Office PowerPoint
Цели, задачи дидактического материала
формировать знания и умения по построению графиков функций;
развивать навыки самостоятельной деятельности учащихся;
формирование и развитие познавательного интереса учащихся.
Содержание дидактического материала (раскрыть подробно)
Презентация содержит справочный материал по теме «Преобразования графиков функций». Состоит из нескольких разделов: правила преобразований, графические иллюстрации правил преобразований, примеры построения графиков функций с помощью преобразований.
Ресурсы дидактического материала (видео-фото, графические изображения, звуковые файлы, ссылки, анимационные и другие эффекты и т.п.)
Анимационные эффекты
Используемые источники информации (литература, Интернет, ЦОР и др.)
Учебники: А.Н.Колмогоров и др. «Алгебра и начала анализа 10-11», А.Г.Мордкович «Алгебра 8», А.Г.Мордкович «Алгебра 9», А.Г.Мордкович «Алгебра и начала анализа 10-11», Ю.Н.Макарычев и др. «Алгебра 9», Ю.Н.Макарычев и др. «Алгебра 9 с углубленным изучением математики».
Единая коллекция ЦОР https://School-collection.edu.ru
Возможности использования дидактического материала:
— педагогом на уроке (указать этапы урока);
— учащимися
Для использования учителем при объяснении нового материала и при повторении ранее изученного.
Данный материал обобщает традиционный учебник. Дидактический материал также предназначен для работы дома, для самостоятельного изучения или повторения данной темы.
Ограничения на использование ресурса (да, нет), описание ограничений
нет
Подробное объяснение места медиа-, мультимедиа компонента в структуре и содержании урока и пояснения по методике их использования в образовательном процессе.
Презентация будет полезна как при объяснении нового материала, так и при повторении темы «Построение графиков функций» в 9-10 -11 классах.
Использование дидактического материала позволяет сократить время на изучение или повторение, позволяет поддерживать устойчивое внимание, повышает интерес к предмету. Учитель может строить объяснение урока с использованием анимации в презентации с целью большего понимания излагаемой темы и наглядности.
Источник
Ìàñøòàáèðîâàíèå — îïåðàöèÿ ñæàòèÿ èëè ðàñòÿæåíèÿ ãðàôèêà ôóíêöèè âäîëü îñåé àáñöèññ è îðäèíàò.
Òî, ÷òî òðåáóåòñÿ âûïîëíèòü ìàñøòàáèðîâàíèå, ïîêàçûâàþò êîýôôèöèåíòû k1 è k2 â óðàâíåíèè y = ± k1 f (± k2 (x + a))+b. Îíè äîëæíû áûòü íå ðàâíû åäèíèöå.
Êîãäà 0 < k1,2 <1, ñîâåðøàåì ñæàòèå ãðàôèêà îòíîñèòåëüíî y è ðàñòÿæåíèå îòíîñèòåëüíî x , êîãäà k1,2>1, âûïîëíÿåì ðàñòÿæåíèå âäîëü îñè îðäèíàò è ñæàòèå âäîëü îñè àáñöèññ.
Êîãäà ôóíêöèÿ ïðèíèìàåò âèä y = f (k2x) ,òî åñëè k2 >1 – ïðîèçâîäèì ñæàòèå ãðàôèêà ê îñè îðäèíàò (y) â k ðàç, à åñëè 0 < k2<1 — ðàñòÿæåíèå ãðàôèêà îò îñè îðäèíàò â 1/k.
Êîãäà ôóíêöèÿ ïðèíèìàåò âèä y = k1 f (x) , òî åñëè k1 >1 — îñóùåñòâëÿåì ðàñòÿæåíèå ãðàôèêà îò îñè àáñöèññ (0x) â k ðàç, à åñëè 0 < k1<1 — ñæàòèå ãðàôèêà ê îñè àáñöèññ â 1/k.
Êàëüêóëÿòîðû ïî àëãåáðå | |
| Ðåøåíèÿ, ïîäñêàçêè è ó÷åáíèê ëèíåéíîé àëãåáðû îíëàéí (âñå êàëüêóëÿòîðû ïî àëãåáðå). | |
| Êàëüêóëÿòîðû ïî àëãåáðå | |
Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû | |
| Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû: êîðíè, äðîáè, ñòåïåíè, óðàâíåíèÿ, ôèãóðû, ñèñòåìû ñ÷èñëåíèÿ è äðóãèå êàëüêóëÿòîðû. | |
| Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû | |
Àëãåáðà 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó àëãåáðû äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Àëãåáðà 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
Ãðàôèêè ýëåìåíòàðíûõ ôóíêöèé | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó ìàòåìàòèêè äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Ãðàôèêè ýëåìåíòàðíûõ ôóíêöèé | |
Ôóíêöèÿ. Ïîêàçàòåëüíàÿ ôóíêöèÿ. | |
| Ïîêàçàòåëüíîé íàçûâàåòñÿ ôóíêöèÿ ó = à õ , â êîòîðîé à ýòî ïîñòîÿííîå ïîëîæèòåëüíîå ÷èñëî. | |
| Ôóíêöèÿ. Ïîêàçàòåëüíàÿ ôóíêöèÿ. | |
Ôóíêöèÿ. Ëèíåéíûå ôóíêöèè. | |
| Åñëè ïåðåìåííûå õ, ó âûðàæàþòñÿ ïîñðåäñòâîì óðàâíåíèÿ Àõ + By = Ñ , ïðè ýòîì ÷èñëà À,  èëè ïî ìåíüøåé ìåðå îäíî èç íèõ, íå ðàâíî íóëþ, òî ãðàôèêîì ôóíêöèîíàëüíîé çàâèñèìîñòè ÿâëÿåòñÿ ïðÿìàÿ ëèíèÿ . | |
| Ôóíêöèÿ. Ëèíåéíûå ôóíêöèè. | |
Источник
