Растяжение сжатие стержней решение
Пример решения задачи на растяжение и сжатие
.
Условие задачи на растяжение и сжатие
Стальной стержень (модуль Юнга кН/см2) с размерами см; см, см и площадью поперечного сечения нижнего участка см2, а верхнего – см2 нагружен внешними осевыми силами кН и кН. Построить эпюры продольных сил и нормальных напряжений . Оценить прочность стержня, если предельное напряжение (предел текучести) кН/см2, а допускаемый коэффициент запаса . Найти удлинение стержня .
Расчетная схема для задачи на растяжение и сжатие
рис 3.2
Решение пример задачи на растяжение и сжатие
Определяем значение опорной реакции , возникающей в заделке
Учитывая, что , направим опорную реакцию вниз. Тогда из уравнения равновесия находим:
кН.
Строим эпюру продольных сил
Разбиваем длину стержня на три участка. Границами участков являются сечения, в которых приложены внешние силы и (или) изменяется размер поперечного сечения стержня.
Воспользуемся методом сечений. Делаем по одному сечению в произвольном месте каждого из трех участков стержня.
Cечение 1 – 1. Отбросим (или закроем листком бумаги) верхнюю часть стержня (рис. 3.2, б). Само сечение 1 – 1 мысленно считаем неподвижным. Мы видим, что внешняя сила растягивает рассматриваемую нижнюю часть стержня. Отброшенная нами верхняя часть стержня противодействует этому растяжению. Это противодействие мы заменим внутренней продольной силой , направленной от сечения и соответствующей растяжению. Разрушения стержня не произойдет только в том случае, если возникающая в сечении 1 – 1 внутренняя продольная сила уравновесит внешнюю силу . Поэтому очевидно, что
кН.
Сечение 2 – 2. Внешняя сила растягивает рассматриваемую нами нижнюю часть стержня, а сила ее сжимает (напомним, что 2 – 2 мы мысленно считаем неподвижным). Причем, согласно условию задачи, . Чтобы уравновесить эти две силы, в сечении 2 – 2 должна возникнуть внутренняя сила , противодействующая сжатию, то есть направленная к сечению. Она равна:
кН.
Сечение 3 – 3. Отбросим теперь часть стержня, расположенную ниже этого сечения. Внутренняя продольная сила должна уравновесить внешнюю (реактивную) сжимающую силу . Поэтому она направлена к сечению и равна:
кН.
Легко убедиться в том, что полученный результат не изменится, если мы отбросим не нижнюю, а верхнюю часть стержня. В этом случае продольная сила также противодействует сжатию. Она равна:
кН.
При построении эпюры продольных сил будем пользоваться следующим правилом знаков: внутренняя продольная сила, возникающая в поперечном сечении стержня, считается положительной, если она противодействует растяжению стержня, и отрицательной, если она противодействует его сжатию. Оно вводится для того, чтобы можно было наглядно видеть, какая часть стержня испытывает деформацию растяжения, а какая часть – деформацию сжатия. Это обстоятельство может оказаться крайне важным, в частности для стержней из хрупкого материала, которые имеют разные допускаемые напряжения на растяжение и на сжатие.
Таким образом, мы установили, что в любом сечении нижнего участка стержня внутренняя продольная сила противодействует растяжению и равна кН. В любом сечении среднего и верхнего участков стержня имеет место деформация сжатия, поэтому кН.
Для построения эпюры продольных сил проводим тонкой линией ось, параллельную оси стержня z (рис. 3.2, д). Вычисленные значения продольных сил в выбранном масштабе и с учетом их знака откладываем от этой вертикальной оси. В пределах каждого из участков стержня продольная сила остается постоянной, поэтому мы как бы «заштриховываем» горизонтальными линиями соответствующий участок.
Отметим, что каждая линия «штриховки» (то есть ордината эпюры) в принятом масштабе дает значение продольной силы в соответствующем поперечном сечении стержня.
Полученную эпюру обводим жирной линией.
Анализируя полученную эпюру, мы видим, что в местах приложения внешних сил на эпюре имеет место скачкообразное изменение продольной силы на величину, равную значению соответствующей внешней силы. Причем изменение поперечного размера стержня, как это видно из рис. 3.2, д, никак не сказывается на характере эпюры .
Строим эпюру нормальных напряжений
Нормальное напряжение, возникающее в k–м поперечном сечении стержня при растяжении (сжатии), вычисляется по следующей формуле
,
где и – продольная сила и площадь k–го поперечного сечения стержня соответственно.
В первом поперечном сечении стержня нормальное напряжение равно
кН/см2,
во втором –
кН/см2,
в третьем –
кН/см2.
Строим по вычисленным значениям эпюру (рис. 3.2, е). В пределах каждого из участков стержня напряжения постоянны, то есть эпюра напряжений параллельна оси. Заметим, что в отличие от эпюры N, на эпюре «скачок» имеет место не только в местах приложения внешних сил, но и там, где происходит изменение размеров поперечного сечения стержня.
Оцениваем прочность стержня
Сопоставляем наибольшее (по модулю) нормальное напряжение , которое в нашем примере возникает во втором сечении стержня, с допускаемым напряжением . Напомним, что допускаемое напряжение представляет собой долю от предельного напряжения , то есть от напряжения, при котором начинается разрушение материала. Разрушение стали, как пластичного материала, начинается при появлении значительных остаточных деформаций. Поэтому для стали предельное напряжение равно пределу текучести: . Тогда
кН/см2.
Условие прочности имеет вид . В нашем случае
кН/см2 > кН/см2,
следовательно, прочность стержня на втором участке не обеспечена.
Таким образом, площадь поперечного сечения стержня на втором участке, равную см2, нам необходимо увеличить.
Несложный анализ показывает, что на других участках стержня условие прочности выполняется.
Из условия прочности определяем требуемую площадь поперечного сечения стержня на втором участке:
см2.
Принимаем на втором участке см2.
Вычисляем удлинение всего стержня
При переменных по длине стержня значениях продольной силы и площади поперечного сечения удлинение вычисляется по формуле
,
где E – модуль Юнга, а – длина соответствующего участка стержня.
Тогда
см.
Таким образом, длина стержня уменьшается на мм.
Задача по сопромату на растяжение и сжатие для самостоятельного решения
Условие задачи на растяжение и сжатие
Стальной стержень (модуль Юнга кН/см2) находится под действием внешних осевых сил и (рис. 3.1). Построить эпюры продольных сил и нормальных напряжений . Оценить прочность стержня, если предельное напряжение (предел текучести) кН/см2, а допускаемый коэффициент запаса . Найти удлинение стержня .
Схемы для задачи на растяжение и сжатие
Исходные данные к задаче на растяжение и сжатие
Номер схемы | F, см2 | a, м | b, м | c, м | P, кН |
1 | 2,0 | 1,2 | 1,4 | 1,6 | 11 |
2 | 2,2 | 1,4 | 1,6 | 1,4 | 12 |
3 | 2,4 | 1,8 | 1,6 | 1,2 | 13 |
4 | 2,6 | 1,6 | 2,0 | 1,0 | 14 |
5 | 2,8 | 2,0 | 1,8 | 1,2 | 15 |
6 | 3,0 | 2,2 | 1,6 | 1,4 | 16 |
7 | 3,2 | 2,4 | 1,4 | 1,6 | 17 |
8 | 3,4 | 2,6 | 1,2 | 1,8 | 18 |
9 | 3,6 | 2,8 | 1,0 | 1,4 | 19 |
3,8 | 2,4 | 1,6 | 1,2 | 20 |
Источник
Первая тема сопротивления материалов — это растяжение-сжатие. Задачи на растяжение сжатие в сопромате — довольно простая тема. И сейчас я это докажу.
Прежде всего растяжение — мы интуитивно понимаем — удлинение, увеличение размеров. А сжатие — уменьшение длины, укорочение.
При изучении растяжения-сжатия используется один и тот же подход ко всем задачам, ко всем расчетным схемам. А именно — метод сечений. О нем мы расскажем в отдельной записи. А пока, ниже вы видите видео уроки на эту тему. Надеюсь вам будет полезно и удобно изучать эту тему со мной.
Что такое растяжение-сжатие
Прежде всего нужно сказать, что растяжение-сжатие — это такой вид деформации (относительного изменения размеров), при котором одно плоское сечение относительно другого удаляется параллельно исходному положению.
Все это звучит сложно, но посмотрите видео и Вы все поймете!
Подход в решении задач на растяжение-сжатие
Видео урок — Как отличить растяжение от сжатия. Приводится объяснение основного метода расчета задач по сопротивлению материалов — метод сечений
В первом видео уроке объясняется сам процес возникновения деформации растяжения-сжатия. Как отличить растяжение от сжатия. Приводится объяснение основного метода расчета задач по сопротивлению материалов — метод сечений.
Здесь рассмотрены задачи для стержня, имеющего сплошное поперечное сечение. На такой стержень может действовать как одна сила, так и несколько.
Растяжение-сжатие в стержневых конструкциях
видео урок Растяжение-сжатие в стержневых конструкциях
Во втором видео уроке приводится решение задачи на растяжение-сжатие для системы стержневых конструкций. Приведены методика и план решения задачи по сопротивлению материалов на тему растяжение-сжатие.
Учет собственного веса в задачах сопротивления материалов на растяжение-сжатие
видео урок — Учет собственного веса в задачах сопротивления материалов на растяжение-сжатие
Третья задача на растяжение-сжатие стержней с учетом собственного веса. Приведен пример решения задачи и доступно рассказывается как можно учесть собственный вес конструкции при расчете на растяжение-сжатие.
Растяжение-сжатие с учетом собственного веса в стержнях с двумя участками
Задача на растяжение сжатие, более сложный случай. В этой задаче стержень состоит из нескольких участков. Здесь необходимо учитывать собственный вес — для стержня, испытывающего деформацию растяжения или сжатия, который состоит из нескольких участков. Здесь же приводится методика построения эпюр внутренних усилий при этих видах деформации.
Удлинение стержня при деформации растяжения-сжатия
видео урок — Удлинение стержня при деформации растяжения-сжатия
Приведен пример расчета на растяжение-сжатие когда нужно определить удлинение стержня. Удлинение (при растяжении) или укорочение (при сжатии) — это изменение размеров стержня вдоль оси приложения продольной нагрузки. Об этом в пятом видео уроке.
Определение удлинения стержня с учетом собственного веса при растяжении-сжатии
Определение изменения длины стержня с учетом собственного веса. Особенности формулы для определения удлинения (изменения длины) при растяжении-сжатии с учетом собственного веса.
Итак на этой странице приведены видеоуроки на основные темы в растяжении-сжатии. Планируется запись еще темы в которой будут рассматриваться статически неопределимые задачи на растяжение-сжатие.
Конечно это не все задачи, которые может понадобиться решить реальному инженеру, как инженеру-механику, так и инженеру-строителю. Встречаются разные случаи, когда нужно применять сообразительность.
Метод сечений в задачах на растяжение сжатие
Однако подход в решении всех задач на растяжение-сжатие всегда одинаков и состоит из следующих шагов:
- рассекаем наш стержень (а именно так называют элемент конструкции, который испытывает деформацию растяжения-сжатия)
- рассматриваем равновесие одной из частей стержня рассматривая внешние, приложенные к стержню усилия и внутреннее усилие, которое формируется силами межатомного взаимодействия
- внутреннее усилие направляем от сечения рассматриваемой части стержня к оставшейся части стержня (для статически определимых систем) или используя интуицию и опыт направляем так, чтобы направление внутреннего усилия совпало с направлением действия деформации (на растяжение или на сжатие)
- из суммы проекций на соответствующую ось или, если это возможно, суммы моментов относительно точки находим нужное внутреннее усилие.
В статически неопределимой задаче нужно к указанным действиям добавить еще одно уравнение которое называется деформационным.
Растяжение-сжатие в сопротивлении материалов одна из наиболее простых тем, разнообразие задач, правда, довольно широко. Но именно растяжение-сжатие в сопротивлении материалов учит тому, как нужно правильно и везде одинаково, несмотря на разнообразие расчетных схем, применять один и тот же подход к решению — метод сечений. В классическом курсе сопротивления материалов это первая тема — растяжение-сжатие.
список видео уроков по сопромату в котором темы раскрываются одна за другой. рекомендую для изучения сопромата
Ну а если возникнут сложности, если Вы предпочитаете заниматься индивидуально — обратитесь ко мне — помогу!
skype: zabolotnyiAN,
e-mail: zabolotnyiAN@gmail.com
Остались вопросы?
Все вопросы, которые у Вас могут возникнуть — рассмотрены в рубрике Условия и цена онлайн обучения сопромат и строймех. Для связи со мной используйте страницу «Контакты» или всплывающий внизу справа значок мессенджера.
Рубрики
Задачи по сопротивлению материалов с решениями, примеры, Растяжение — сжатие, Сопромат онлайн
Метки
внутренние усилия, задачи курса сопротивление материалов, классический курс сопротивления материалов в решениях задач, краткий курс сопротивления материалов, курс сопромата для чайников, Построение эпюр продольных сил, растяжение сжатие сопромат, растяжение сжатие сопротивление материалов, сопромат для чайников, Сопромат Примеры решения задач на растяжение-сжатие, сопромат репетитор, Сопромат это легко, Сопротивление материалов, сопротивление материалов краткий курс, сопротивление материалов примеры решения задач, эпюры растяжения сжатия
Источник
Главная
Расчеты на растяжение и сжатие
статически определимых стержневых систем
Пример 1.
Абсолютно
жесткий брус ВС (ЕВС = ) прикреплен в точке С к неподвижному шарниру (см.
рис.), а в точке В поддерживается
стальной тягой АВ. В точке В приложена вертикальная сила F = 20 кН.
Подобрать
сечение тяги АВ и показать перемещение
точки В. Расчетное сопротивление
стали растяжению коэффициент условий работы а модуль упругости
стали тяги АВ –
Решение.
Вырежем
мысленно узел В (рис. б) и составим для него уравнения
равновесия:
откуда находим
откуда
Окончательно
имеем
Следовательно,
брус ВС сжат силой N2, а элемент АВ растянут силой N1.
Подбор сечения
тяги АВ проводим по формуле откуда определяем
Предположим,
что тяга АВ имеет круглое поперечное
сечение, тогда An =
1,44 см2 = , откуда находим r =
0,677 смиd = 1,35 см.
Определим
удлинения стержней АВ и СВ:
Таким образом, точка В переместится в точку В/
по дуге окружности радиусом , причем расстояние между точками А и В/будет равно
Пример 2.
Определить из расчетов на прочность и жесткость
допускаемую силу F, если [] = 120 МПа, [] = 1,7 мм, А1 = 2А, А2 = А = 5 см2, l1 = l2 = l = 1 м, Е = 200 ГПа.
Р е ш е н и е.
1. Определение усилий в стержнях.
Из условия равновесия бруса АС имеем
, , ;
, , .
2. Расчет на прочность.
Находим напряжения в
стержнях
,
.
Как видим, наиболее
нагруженным является 2-й стержень, прочность которого предопределяет прочность
всей конструкции в целом. Из условия прочности находим = 30 кН.
3. Расчет на жесткость.
Вычисляем деформации
стержней
,
,
а по ним перемещение точки С. Из подобия треугольников В1А1В2 и С1А1С2 имеем:
В1В2/А1В2 = С1С2/А1С2 или ,
откуда .
Записываем условие жесткости ,
откуда = 200×109×5×10-4×1,7×10-3/(8,5×1)= 20 кН.
Допускаемая нагрузка из расчета на жесткость
получилась меньше, чем из расчета на прочность, поэтому ее и принимаем в качестве окончательной, т.е.
кН.
Пример 3.
К двум
одинаковым стержням приложена сила F.
Установить, при каком угле конструкция будет
иметь наименьший вес?
Р е ш е н и е.
Вес
конструкции является функцией угла , т.е. .
Нам необходимо установить такой угол, при котором
функция принимает минимальное значение. В теории оптимального
проектирования она называется целевой функцией.
Для
определения веса стержневой системы нужно знать площади сечений стержней. Из
условия равновесия узла С находим
усилия в стержнях:
, , ,
а из условия
прочности – площади их поперечных сечений:
, откуда .
Учитывая, что
длины стержней , находим вес конструкции (целевую функцию):
.
Функция принимает минимальное
значение, когда
, откуда и .
Определение грузоподъемности
статически определимой конструкции, работающей на растяжение-сжатие. Расчет по
допускаемым напряжениям
При таком
подходе несущая способность конструкции отождествляется с несущей способностью
наиболее нагруженного элемента. Последовательность расчета при этом выглядит
следующим образом.
Составляются уравнения статики и по числу лишних неизвестных –
дополнительные уравнения совместности деформаций. Решая полученную систему,
определяют усилия в стержнях и связанные с ними напряжения. Из сопоставления
напряжений в наиболее нагруженном элементе с допустимой величиной делается
заключение о надежности конструкции либо определяются искомые величины (размеры
сечения стержней, допускаемая нагрузка).
Пример 4.
Конструкция,
состоящая из стержней, соединенных шарнирами, загружена силой F (см. рис. 1). Сечения стержней – из
прокатной стали и площади сечений можно найти по таблицам сортамента прокатной
стали. Цель расчета:
1. определить
значение допускаемой нагрузки;
2. найти
перемещение узла С.
Рис.1
Решение.
Для
определения усилий используем метод сечений. Для этого нарисуем план сил
(рис.2): рассечем деформируемые стержни конструкции и отброшенные части
стержней заменим продольными силами N1 и N2 .
Рис.2
Из уравнений
равновесия отсеченной части конструкции найдем продольные силы в стержнях:
и .
Знак минус показывает,
что направление усилия в стержне 2 противоположно показанному на плане сил,
т.е. стержень 2 сжат.
Определим
напряжения по и выберем наиболее напряженный стержень (допустим, что в рассматриваемой задаче
это будет стержень 1).
Из условия прочности этого стержня получим значение
допускаемой нагрузки:
, .
Найдем
перемещение узла С,
построив план перемещений (рис.3).
Рис.3
Предварительно
найдем абсолютные деформации стержней и по формуле . В
рассматриваемой задаче растянутый стержень 1 будет удлиняться, а сжатый
стержень 2 – укорачиваться. Для построения плана перемещений нарисуем схему
конструкции в масштабе и отложим отрезки и вдоль оси каждого
стержня, выбрав масштаб для деформаций так, чтобы картинка плана перемещений
была наглядной. В процессе деформации стержни поворачиваются относительно точек
А и В по дугам. Из-за малости деформаций эти дуги заменяем
касательными, т. е. перпендикулярами к направлениям стержней (отрезки и на плане перемещений).
На пересечении дуг (перпендикуляров к направлениям стержней) находится новое
положение узла C после деформации –
точка на плане перемещений.
Вертикальное и горизонтальное перемещение узла C допускается определять по масштабу, не делая сложных
геометрических выкладок.
Примечание. Если конструкция имеет
абсолютно жесткий стержень, то принцип
построения плана перемещений тот же. Все точки абсолютно жесткого стержня могут
перемещаться только по дугам (перпендикулярам к направлению стержня), поворачиваясь
вокруг неподвижного шарнира. Например, если стержень АС на плане перемещений считать абсолютно жестким, то точка Спереместится в положение и горизонтальное
перемещение узла С будет равно нулю.
Пример 5.
Для схемы, изображенной на рис.1 необходимо:
Рис.1
1) Определить площадь поперечного сечения стержней при действии силы F и подобрать угловую равнополочную
или неравнополочную сталь, при условии, что поперечное
сечение одного из стержней в два раза больше, чем другого.
2) Определить напряжения в стержнях:
— от действия силы F;
— от неточности монтажа, если считать, что один из стержней выполнен
короче на величину ;
— от изменения температуры.
3) Определить суммарные напряжения от действия внешних сил, от неточности
монтажа и от изменения температуры.
4) Подсчитать недонапряжения или перенапряжения
в стержнях.
Дано: F=100 кН, а =
1,2м, b = 0,8м, = 0,2мм, = 20°С, Е = 2×105МПа,
= 125×10-71/гр, [] = 100 МПа.
Решение.
Определим необходимую по условию прочности площадь поперечного сечения
стержней.
1) Находим степень статической неопределимости.
2.1) Статическая сторона задачи
; ;
; ;
; .
2.2) Геометрическая сторона задачи (рис.2)
~Þ
; ; ;
2.3) Физическая сторона задачи
;
Рис.2
2.4) Синтез
Подставим выражения, полученные в физической стороне задачи, в выражения
из геометрической стороны задачи и приведем подобные.
Решим совместно систему уравнений, составленную из полученного выражения
для N1 и уравнения моментов из статической стороны
задачи.
2.5) Определяем площадь поперечного сечения стержней
Определим, какой из стержней нагружен сильнее.
;
Второй стержень является более нагруженным, так как , поэтому запишем для него условие прочности и
определим площадь поперечного сечения.
Подбираем по справочнику угловую равнополочную сталь № 70´5
ГОСТ8509-86 (SТ= 6,86 см2).
2.6) Определяем напряжения в стержнях от внешних сил
Первый стержень работает на сжатие, а второй – на растяжение.
3) Определим напряжения в стержнях от неточности монтажа
Будем считать, что короткий стержень выполнен короче на величину (см.рис.3).
Рис.3
3.1) Статическая сторона задачи
; ;
; ;
; .
3.2) Геометрическая сторона задачи
~Þ
; ; ;
3.3) Физическая сторона задачи
;
3.4) Синтез
Подставим в полученное выражение данные из условия задачи и получим:
3.5) Определим напряжения в стержнях
Оба стержня работают на растяжение.
4) Определим напряжения в стержнях от изменения температуры (см. рис. 4).
Рис.4
Будем считать, что температура системы повышается. Тогда оба стержня будут
удлиняться от повышения температуры. При удлинении стержней, они будут
воздействовать друг на друга через недеформируемый стержень АС. Вследствие этого, в обоих стержнях
будут возникать дополнительные силы сжатия.
4.1) Статическая сторона задачи
; ;
; ;
; .
4.2) Геометрическая сторона задачи
~Þ
; ; ;
4.3) Физическая сторона задачи
;
.
4.4) Синтез
Решив уравнение, получим .
4.5) Определим напряжения в стержнях
Оба стержня работают на сжатие.
5) Определим суммарные напряжения в стержнях
6) Найдем недонапряжения или перенапряжения в
стержнях
— недонапряжение
— недонапряжение.
Пример 6.
Дано: Сила F= 100 кН;
расчетное сопротивление стали R =160 МПа; модуль упругости E=2∙105
МПа(рис. а)
Требуется:
1. Определить
усилия в стержнях.
2. Подобрать
размеры поперечных сечений стержней. Стержень 1 стальной, круглого поперечного
сечения, стержень 2 стальной квадратного сечения.
3. Вычислить
удлинения (укорочения) стержней и построить план перемещений.
4. Определить
перемещение узла.
а)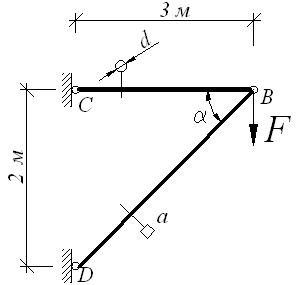 б)
б)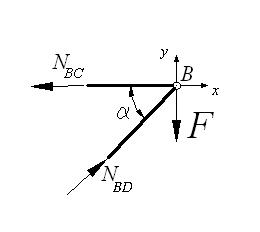
в)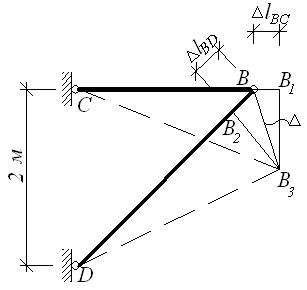 г)
г)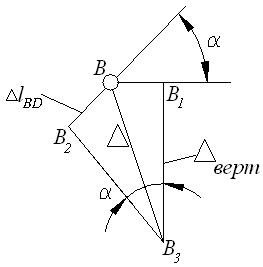
Решение.
Мысленно
вырезаем узел В,
действие отброшенной части кронштейна заменяем искомыми внутренними усилиями.
Для полученной плоской системы сходящихся сил составим уравнения равновесия
(рис. б)
Решив
уравнения, найдем внутренние усилия NBD и NBC
Полученные
положительные значения внутренних усилий показывают, что предварительно
выбранные направления усилий оказались верными, стержень BC
растягивается, а стержень BD сжимается.
Диаметр
стержня BC находим из условия прочности:
где,
откуда .
Размеры поперечного сечения стержня BD определим на условия
прочности:
где ABD = a2,
откуда .
Перемещение
узла В
найдем с помощью графоаналитического метода, для чего вычислим, используя закон
Гука, абсолютные деформации стержней ВС
и BD, предполагая их свободными в точке В:
где
Положение узла В после деформации стержней
определится в результате построения
деформационного треугольника по сторонам и .
Стержень ВС удлинился на величину , концевое сечение
переместилось в точку В1. Радиусом, равным СВ1проведем из точки С
дугу окружности. Так как перемещения малы, то дугу можно заменить касательной,
проведенной через В1
перпендикулярно оси стерня ВС
(рисунок 1, в).
Стержень BD укоротился на , и концевое сечение переместилось в точку В2.
Заменяя дугу, описанную из точки D радиусом DB2касательной,
проведенной через В2перпендикулярно оси стержня BD, получим на
пересечении перпендикуляров точку В3
— новое положение узла В. Соединив
точку В с В3 найдем перемещение узла В. На рисунке 1, в план перемещений изображен в увеличенном масштабе. План
перемещений рекомендуется строить отдельно, как показано на рисунке 1, г. Из него следует, что горизонтальная
составляющая перемещения узла
В равна:
см.
Вертикальную
составляющую перемещения узла
В легко найти,
воспользовавшись теоремой аналитической геометрии – проекция замыкающей на
любую ось равна алгебраической сумме проекций составляющих на ту же ось. Принимая за ось проекций направление получим:
;
откуда .
Знак учтен при построении
плана перемещений. Полное перемещение узла Вбудет равно:
.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин
Теория машин и механизмов
Источник
