Растяжение пружины жесткостью k увеличено на дельта x
I вариант
Часть А.
1. Тело массой m движется со скоростью V. Каков импульс тела?
А. mV². Б. mV². В. mV . Г. mV . Д. mV . Е. mV .
2 2 2 2
2. Тело массой m движется со скоростью V. Какова кинетическая энергия тела?
А. mV². Б. mV². В. mV . Г. mV . Д. mV . Е. mV .
2 2 2 2
3. Тело массой m поднято над поверхностью Земли на высоту h. Какова потенциальная
энергия тела?
А. mg. Б. mgh . В. mh . Г gh . Д. mg .
h
4. Пружина жескостью k под действием силы F растянута на x м. Какова потенциальная
энергия упругой деформации пружины?
А. kx. Б. kx². В. kx. Г. kx². Д. mgh .
2 2
5. Мяч был брошен с поверхности Земли вертикально вверх. Он достиг высшей точки
траектории и затем упал на Землю. В какой момент времени движения полная
механическая энергия мяча имела максимальное значение? Сопротивлением воздуха
пренебречь.
А. В момент начала движения вверх. Б. В момент достижения верхней точки траектории. В. В момент прохождения половины расстояния до верхней точки траектории. Г. В
момент падения на Землю. Д. В течение всего времени полёта полная механическая
энергия была одинакова.
6. Два шара с одинаковыми массами m двигались навстречу друг другу с одинаковыми по
модулю скоростями V. После неупругого столкновения оба шара остановились. Каково
изменение суммы импульсов двух шаров в результате столкновения?
А. mV . Б. 2mV . В. 0 . Г.- mV . Д. — 2mV .
7. Камень брошен вертикально вверх. На пути 1 м его кинетическая энергия уменьшилась
на 16 Дж. Какую работу совершила сила тяжести на этом пути?
А. — 16 Дж. Б.- 4 Дж. В. 16 Дж. Г. 4 Дж. Д. 0 Дж.
8. Какова кинетическая энергия автомобиля массой 1000 кг, движущегося со скоростью 36
км/ч?
А. 36 · 10³ Дж. Б. 648 · 10³ Дж. В. 10 Дж. Г. 5· 10 Дж.
Часть В.
1. Тело поднимается вертикально вверх под действием силы F = 10Н. В начальный момент
времени тело находилось на высоте, равной 1м, от поверхности Земли. Найдите
положение тела в тот момент, когда сила, поднимающая груз, совершила работу,
равную 200 Дж.
2. Недеформированную пружину растягивают на ∆l = 10см. Найдите работу
деформирующей пружину силы, если при растяжении пружины на ∆l˳ = 1см требуется
сила F˳= 4Н. Чему равна работа силы упругости пружины?
II вариант
Часть А.
1. Как называется физическая величина, равная произведению массы тела на вектор его
мгновенной скорости?
А. Импульс тела. Б. Импульс силы. В. Кинетическая энергия. Г. Потенциальная энергия. Д. Двойная кинетическая энергия.
2. Как называется физическая величина, равная половине произведения массы тела на
квадрат его мгновенной скорости?
А. Импульс тела. Б. Импульс силы. В. Кинетическая энергия. Г. Потенциальная энергия. Д. Двойная кинетическая энергия.
3. Как называется физическая величина, равная произведению массы тела m на ускорение
свободного падения и на расстояние h от тела до поверхности Земли?
А. Импульс тела. Б. Импульс силы. В. Кинетическая энергия. Г. Потенциальная энергия. Д. Двойная кинетическая энергия.
4. Растяжение пружины жесткостью k увеличено на ∆x. Как изменилась при этом
потенциальная энергия упругой деформации пружины?
А. Увеличилась на k∆x. Б. Увеличилась на k∆x². В. Увеличилась на k∆x² .
2
Г. Уменьшилась на k∆x. Д. Уменьшилась на k∆x² . Е. Уменьшилась на k∆x² .
2
5. Мяч был брошен с поверхности Земли вертикально вверх. Он достиг высшей точки
траектории и затем упал на Землю. В какой момент времени движения полная
механическая энергия мяча имела минимальное значение? Сопротивлением воздуха
пренебречь.
А. В момент достижения верхней точки траектории. Б. В течение всего времени полёта
полная механическая энергия была одинакова. В. В момент падения на Землю. Г. В
момент прохождения половины расстояния до верхней точки траектории. Д. В момент
начала движения вверх.
6. Два шара с одинаковыми массами m двигались навстречу друг другу с одинаковыми по
модулю скоростями V. После упругого столкновения каждый шар стал двигаться в
обратном направлении с прежней по модулю скоростью. Каково
изменение суммы импульсов двух шаров в результате столкновения?
А. mV . Б. — 2mV . В. 4mV . Г.- 4mV . Д. 0 .
7.. Камень брошен вертикально вверх. На пути 1 м его кинетическая энергия увеличилась
на 16 Дж. Какую работу совершила сила тяжести на этом пути?
А. — 16 Дж. Б.- 4 Дж. В. 16 Дж. Г. 4 Дж. Д. 0 Дж.
8. Какова кинетическая энергия ракеты массой 100 кг, движущегося со скоростью 60
км/мин?
А. 10⁸ Дж. Б. 5 · 10⁷ Дж. В. 1,8 · 10 Дж. Г. 6 · 10³ Дж. Д. 50 Дж.
Часть В.
1. Тело поднимается вертикально вверх под действием силы F = 10Н. В начальный момент
времени тело находилось на высоте, равной 1м, от поверхности Земли. Найдите
положение тела в тот момент, когда сила, поднимающая груз, совершила работу,
равную 300 Дж.
2. Недеформированную пружину растягивают на ∆l = 10см. Найдите работу
деформирующей пружину силы, если при растяжении пружины на ∆l˳ = 1см требуется
сила F˳= 6Н. Чему равна работа силы упругости пружины?
Контрольное тестирование
по дисциплине физика
Коды правильных ответов:
Часть А | Часть В | |||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 1 | 2 | |
1 вариант | Д | Б | Б | Г | Д | В | А | Г | 21 | 2 |
2 вариант | А | В | Г | В | Б | Д | В | Б | 31 | 3 |
Шкала оценки знаний обучающихся по итогам выполнения теста:
Число правильных ответов | 0-2 | 3-4 | 5-6 | 7-8 | 9-10 |
Оценка в баллах | 1 | 2 | 3 | 4 | 5 |
Источник
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Сила упругости — это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Силы, возникающие при пластических деформациях, не относятся к силам упругости.
Понятие о деформациях
Деформация — это изменение формы и размеров тела.
К деформациям относятся: растяжение, сжатие, кручение, сдвиг, изгиб.
Деформации бывают упругими и пластическими.
Закон Гука
Абсолютная величина силы упругости прямо пропорциональна величине деформации. В частности, для пружины, сжатой или растянутой на величину (displaystyle x) (разница между крайними положениями), сила упругости задается формулой [F=kx] где (displaystyle k) — коэффициент жесткости пружины.
Единицы измерения коэффициента жесткости: (k=)[Н/м].
Закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела.
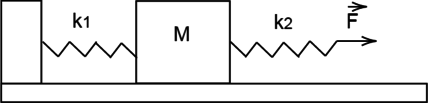
Кубик массой (M = 2) кг, сжатый с боков пружинами, покоится на гладком горизонтальном столе. Первая пружина сжата на 2 см, а вторая сжата на 6 см. Жёсткость первой пружины (k_1 = 1200) Н/м. Чему равна жёсткость второй пружины (k_2)? Ответ выразите в Н/м.
По второму закону Ньютона силы упругости пружин будут уравновешивать друг друга, следовательно: [k_1Delta x_1=k_2Delta x_2] где (Delta x_1) и (Delta x_2) – сжатие первой и второй пружины соответственно.
Откуда жесткость второй пружины [k_2=dfrac{k_1 Delta x_1}{Delta x_2}= dfrac{1200text{ Н/м}cdot 2text{ см}}{6text{ см}}=400text{ Н/м}]
Ответ: 400
На штативе закреплён школьный динамометр. К нему подвесили груз массой 0,1 кг. Пружина динамометра при этом удлинилась на 2,5 см. Чему будет равно удлинение пружины, если масса груза увеличится втрое? (Ответ дайте в сантиметрах)
Согласно закону Гука [F=kDelta x] где k – жесткость пружины, ( Delta x) – удлинение пружины.
Найдем жесткость пружины, зная, что ( Delta x) = 2,5 см = 0,025 м при приложении силы, равно ( F=m_1g=0,1cdot 10=1text{ H} ): [k=dfrac{F}{Delta x}=dfrac{1}{0,025}=40text{ H/кг}] Если массу груза увеличить в 3 раза, то есть, (m_2=0,3) кг, то удлинение пружины будет равно: [Delta x=dfrac{F}{k}=dfrac{m_2g}{k}=dfrac{3cdot0,1cdot10text{ H}}{40text{ H/кг}}=0,075text{ м}=7,5text{ см}]
Ответ: 7,5
К системе из кубика массой M = 3 кг и двух пружин приложена постоянная горизонтальная сила F величиной 20 Н (см. рисунок). Между кубиком и опорой трения нет. Система покоится. Жёсткость первой пружины (k_1 = 400 text{ Н/м}). Жёсткость второй пружины (k_2 = 800 text{ Н/м}). Каково удлинение первой пружины? (Ответ дайте в сантиметрах)

Согласно закону Гука удлинение (Delta x) пружины связано с ее жесткостью k и приложенной к ней силе F выражением (F=kDelta x). На первую пружину действует такая же сила F, что и на вторую, так как трения между кубиком и опорой нет. То, что первая пружина соединена со второй через кубик, здесь не имеет никакого значения, соответственно удлинение первой пружины – это величина, равная: [Delta x=dfrac{F}{k_1}=dfrac{20text{ H}}{400text{ H/м}}=0,05 text{ м}=5 text{ см}]
Ответ: 5
Определите силу, под действием которой пружина жёсткостью 200 Н/см удлинится на 5 мм.
Согласно закону Гука ( F=kDelta x ), где k – жесткость пружины, ( Delta x) – удлинение пружины, получаем: [F=kDelta x=(dfrac{200}{0,01})text{H/м}cdot(5cdot10^{-3})text{м}=100text{ H}]
Ответ: 100
Пружина одним концом прикреплена к неподвижной опоре, к другому концу приложили силу равную 1500 Н, при этом пружина растянулась на 0,2 м. Определите жесткость данной пружины. Ответ дать в Н/м.
После растяжения, пружина покоится и на неё действуют 2 силы направленные в противоположные направления: (F_{text{упр}}) – сила упругости и F – приложенная сила.
Тогда по первому закону Ньютона: [F_{text{упр}}=F] По закону Гука: [F_{text{упр}}=kx] Приравниваем эти формулы: [F=kx] Тогда [k=frac{F}{x}=frac{1500}{0,2}=7500 text{ Н/м}]
Ответ: 7500
К потолку прикреплены одним концом две пружины с одинаковой жесткостью. За другой конец первую пружину растягивают с силой (F_{text{1}}), которая в 2,5 раза больше силы (F_{text{2}}), растягивающей вторую пружину. При этом вторая пружина растянулась на 0,4 м. Насколько растянулась первая пружина? Ответ дать в метрах.
После растяжения обе пружины находятся в покое и на них, кроме данных сил действует сила упругости. Тогда по первому закону Ньютона: [F_{text{упр1}}=F_{text{1}}] [F_{text{упр2}}=F_{text{2}}] где (F_{text{упр1}}) – сила упругости, действующая на первую пружина, (F_{text{упр2}}) – на вторую.
По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [kx_{1}=F_{1}quad(1)] [kx_{2}=F_{text{2}}quad(2)] где (x_{1}) – удлинение первой пружины, (x_{2}) – второй. Разделим (1) на (2), получится: [frac{x_{1}}{x_{2}}=frac{F_{text{1}}}{F_{text{2}}}Rightarrow x_{1}=dfrac{F_{text{1}}x_{2}}{F_{text{2}}}=2,5cdot0,4=1text{ м}]
Ответ: 1
К грузу массой (m) аккуратно подвесили другой груз массой (M), при этом пружина с жесткостью 1200 Н/м удлинилась так, как показано на рисунке. Найдите массу (M). Ускорение свободного падения считать равным 10 м/(c^{2}). Ответ дать в кг.
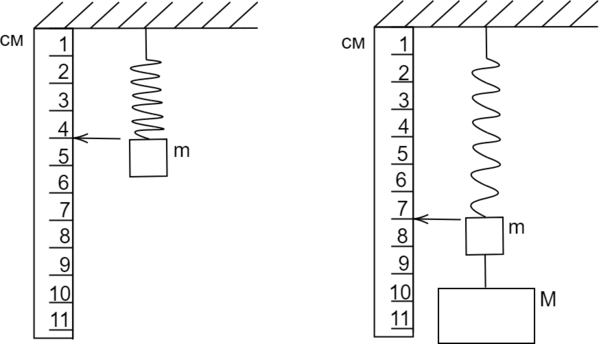
Рассмотрим ситуацию до подвешивания груза: система тел “груз и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg=F_{text{упр}1}] Рассмотрим ситуацию после подвешивания груза: систама тел “2 груза и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg+Mg=F_{text{упр2}}] По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [mg=kx_{1}quad(1)] [mg+Mg=kx_{2}quad(2)] Вычтем (1) из (2), получится: [Mg=k(x_{2}-x_{1})Rightarrow M=dfrac{k(x_{2}-x_{1})}{g}=frac{1200cdot0,03}{10}=3,6text{ кг}]
Ответ: 3,6
Источник
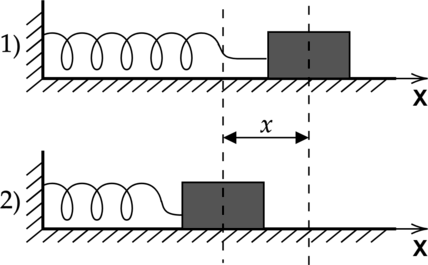
Груз пружинного маятника покоится на горизонтальном гладком столе. Масса груза m, жёсткость пружины k, пружина сначала не растянута. Покоящемуся грузу быстро сообщают скорость направленную вдоль оси пружины, от вертикальной стенки.
Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
А) максимальное растяжение пружины
Б) модуль ускорения груза в момент максимального растяжения пружины
1)
2)
3)
4)
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
В начале движения потенциальная энергия системы равна нулю, а в точке, где растяжение пружины максимально кинетическая энергия системы равна нулю. По закону сохранения энергии:
В данном случае ускоряющая сила — это сила Гука. В момент максимального растяжения пружины
Источник: phys-ege.sdamgia.ru
Формула жесткости пружины
Определение и формула жесткости пружины
Силу, которая возникает в результате деформации тела и пытающаяся вернуть его в исходное состояние, называют силой упругости.
Чаще всего ее обозначают $>_$. Сила упругости появляется только при деформации тела и исчезает, если пропадает деформация. Если после снятия внешней нагрузки тело восстанавливает свои размеры и форму полностью, то такая деформация называется упругой.
Современник И. Ньютона Р. Гук установил зависимость силы упругости от величины деформации. Гук долго сомневался в справедливости своих выводов. В одной из своих книг он привел зашифрованную формулировку своего закона. Которая означала: «Ut tensio, sic vis» в переводе с латыни: каково растяжение, такова сила.
Рассмотрим пружину, на которую действует растягивающая сила ($overline$), которая направлена вертикально вниз (рис.1).
Силу $overline$ назовем деформирующей силой. От воздействия деформирующей силы длина пружины увеличивается. В результате в пружине появляется сила упругости ($>_u$), уравновешивающая силу $overline$. Если деформация является небольшой и упругой, то удлинение пружины ($Delta l$) прямо пропорционально деформирующей силе:
где в коэффициент пропорциональности называется жесткостью пружины (коэффициентом упругости) $k$.
Жесткость (как свойство) — это характеристика упругих свойств тела, которое деформируют. Жесткость считают возможностью тела оказать противодействие внешней силе, способность сохранять свои геометрические параметры. Чем больше жесткость пружины, тем меньше она изменяет свою длину под воздействием заданной силы. Коэффициент жесткости — это основная характеристика жесткости (как свойства тела).
Коэффициент жесткости пружины зависит от материала, из которого сделана пружина и ее геометрических характеристик. Например, коэффициент жесткости витой цилиндрической пружины, которая намотана из проволоки круглого сечения, подвергаемая упругой деформации вдоль своей оси может быть вычислена как:
где $G$ — модуль сдвига (величина, зависящая от материала); $d$ — диаметр проволоки; $d_p$ — диаметр витка пружины; $n$ — количество витков пружины.
Единицей измерения коэффициента жесткости в Международной системе единиц (Си) является ньютон, деленный на метр:
Коэффициент жесткости равен величине силы, которую следует приложить к пружине для изменения ее длины на единицу расстояния.
Формула жесткости соединений пружин
Пусть $N$ пружин соединены последовательно. Тогда жесткость всего соединения равна:
где $k_i$ — жесткость $i-ой$ пружины.
При последовательном соединении пружин жесткость системы определяют как:
Примеры задач с решением
Задание. Пружина в отсутствии нагрузки имеет длину $l=0,01$ м и жесткость равную 10 $frac. $Чему будет равна жесткость пружины и ее длина, если на пружину действовать силой $F$= 2 Н? Считайте деформацию пружины малой и упругой.
Решение. Жесткость пружины при упругих деформациях является постоянной величиной, значит, в нашей задаче:
При упругих деформациях выполняется закон Гука:
[F=kDelta l left(1.2right).]
Из (1.2) найдем удлинение пружины:
Длина растянутой пружины равна:
Вычислим новую длину пружины:
Ответ. 1) $k’=10 frac$; 2) $l’=0,21$ м
Задание. Две пружины, имеющие жесткости $k_1$ и $k_2$ соединили последовательно. Какой будет удлинение первой пружины (рис.3), если длина второй пружины увеличилась на величину $Delta l_2$?
Решение. Если пружины соединены последовательно, то деформирующая сила ($overline$), действующая на каждую из пружин одинакова, то есть можно записать для первой пружины:
Для второй пружины запишем:
Если равны левые части выражений (2.1) и (2.2), то можно приравнять и правые части:
[k_1Delta l_1=k_2Delta l_2left(2.3right).]
Из равенства (2.3) получим удлинение первой пружины:
Ответ. $Delta l_1=frac$
Источник: www.webmath.ru
Максимальное растяжение пружины формула
При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости .
Простейшим видом деформации являются деформации растяжения и сжатия (рис. 1.12.1).
| Рисунок 1.12.1. При малых деформациях () сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации: Это соотношение выражает экспериментально установленный закон Гука . Коэффициент называется жесткостью тела . В системе СИ жесткость измеряется в ньютонах на метр (). Коэффициент жесткости зависит от формы и размеров тела, а также от материала. В физике закон Гука для деформации растяжения или сжатия принято записывать в другой форме. Отношение называется относительной деформацией , а отношение , где – площадь поперечного сечения деформированного тела, называется напряжением . Тогда закон Гука можно сформулировать так: относительная деформация пропорциональна напряжению : Коэффициент в этой формуле называется модулем Юнга . Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Модуль Юнга различных материалов меняется в широких пределах. Для стали, например, , а для резины , т. е. на пять порядков меньше. Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рис. 1.12.2).
|
Источник
