Растяжение пружины в положении равновесия бруска

Подробности
Просмотров: 896
«Физика — 10 класс»
При решении задач по этой теме надо иметь в виду, что закон Гука справедлив только при упругих деформациях тел. Сила упругости не зависит от того, какая происходит деформация: сжатия или растяжения, она одинакова при одинаковых Δl. Кроме этого, считается, что сила упругости вдоль всей пружины одинакова, так как масса пружины обычно не учитывается.
Задача 1.
При помощи пружинного динамометра поднимают с ускорением а = 2,5 м/с2, направленным вверх, груз массой m = 2 кг. Определите модуль удлинения пружины динамометра, если её жёсткость k = 1000 Н/м.

Р е ш е н и е.
Согласно закону Гука, выражающему связь между модулем внешней силы  , вызывающей растяжение пружины, и её удлинением, имеем F = kΔl. Отсюда
, вызывающей растяжение пружины, и её удлинением, имеем F = kΔl. Отсюда 
Для нахождения силы  воспользуемся вторым законом Ньютона. На груз, кроме силы тяжести m
воспользуемся вторым законом Ньютона. На груз, кроме силы тяжести m , действует сила упругости пружины, равная по модулю F и направленная вертикально вверх. Согласно второму закону Ньютона m
, действует сила упругости пружины, равная по модулю F и направленная вертикально вверх. Согласно второму закону Ньютона m = F + m
= F + m .
.
Направим ось OY вертикально вверх так, чтобы пружина была расположена вдоль этой оси (рис. 3.16). В проекции на ось OY второй закон Ньютона можно записать в виде mау = Fy + mgy
Так как ау = a, gy = -g и Fy = F, то F = mа + mg = m(а + g).
Следовательно,

Задача 2.
Определите, как изменяется сила натяжения пружины, прикреплённой к бруску массой m = 5 кг, находящемуся неподвижно на наклонной поверхности, при изменении угла наклона от 30° до 60°. Трение не учитывайте.

Р е ш е н и е.
На брусок действуют сила тяжести, сила натяжения пружины и сила реакции опоры (рис. 3.17).
Условие равновесия бруска: m +
+  +
+  yпp = 0.
yпp = 0.
Запишем это условие в проекциях на оси ОХ и OY: 
Из первого уравнения системы получим Fyпp = mg sinα.
При изменении угла наклона изменение силы упругости найдём из выражения ΔFyпp = mg(sinα2 — sinα1) = 5 • 10 • (0,866 — 0,5) (Н) = 18,3 Н.
Задача 3.
К потолку подвешены последовательно две невесомые пружины жёсткостями 60 Н/м и 40 Н/м. К нижнему концу второй пружины прикреплён груз массой 0,1 кг. Определите жёсткость воображаемой пружины, удлинение которой было бы таким же, как и двух пружин при подвешивании к ней такого же груза (эффективную жёсткость).

Р е ш е н и е.
Так как весом пружин можно пренебречь, то очевидно, что силы натяжения пружин равны (рис. 3.18). Тогда согласно закону Гука
Fynp1 = Fупр2; k1x1 = k2х2. (1)
На подвешенный груз действуют две силы — сила тяжести и сила натяжения второй пружины.
Условие равновесия груза запишем в виде mg = k2х2.
Из этого уравнения найдём удлинение

Подставив выражение для х2 в уравнение (1), получим для удлинения

Определим теперь эффективную жёсткость. Запишем закон Гука для воображаемой пружины:

Подставив в формулу (2) выражения для удлинений x1 и х2 пружин, получим

Для эффективной жёсткости получим выражение

Задача 4.
Через блок, закреплённый у края стола, перекинута нерастяжимая нить, к концам которой привязаны брусок массой m1 = 1 кг, находящийся на горизонтальной поверхности стола, и пружина жёсткостью k = 50 Н/м, расположенная вертикально. Ко второму концу пружины привязана гиря массой m2 = 200 г (рис. 3.19). Определите удлинение пружины при движении тел. Силу трения, массы пружины, блока и нити не учитывайте.

Р е ш е н и е.
На брусок действуют сила тяжести, сила реакции опоры и сила натяжения нити.
На гирю действуют сила тяжести и сила натяжения пружины.
Согласно второму закону Ньютона для бруска и гири запишем:
m1 1 = m1
1 = m1 +
+  +
+  ;
;
m2 2 = m
2 = m +
+  упр.
упр.
В проекциях на выбранные оси координат запишем: на ось ОХ: m1а1 = Т;
на ось OY:

Так как нить нерастяжима, то модули ускорений равны: а1 = а2 = а.
В силу условия малых масс пружины, нити и блока можно записать: T2 = Fупр и Т1 = Т2 = Т.
Учтя последние равенства, систему уравнений (1) запишем в виде

Выразив ускорение из первого уравнения системы и подставив его во второе, получим

Из этого уравнения найдём силу натяжения нити:

Так как согласно закону Гука Fупр = kx, то

Тогда удлинение пружины

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Динамика — Физика, учебник для 10 класса — Класс!ная физика
Основное утверждение механики —
Сила —
Инертность тела. Масса. Единица массы —
Первый закон Ньютона —
Второй закон Ньютона —
Принцип суперпозиции сил —
Примеры решения задач по теме «Второй закон Ньютона» —
Третий закон Ньютона —
Геоцентрическая система отсчёта —
Принцип относительности Галилея. Инвариантные и относительные величины —
Силы в природе —
Сила тяжести и сила всемирного тяготения —
Сила тяжести на других планетах —
Примеры решения задач по теме «Закон всемирного тяготения» —
Первая космическая скорость —
Примеры решения задач по теме «Первая космическая скорость» —
Вес. Невесомость —
Деформация и силы упругости. Закон Гука —
Примеры решения задач по теме «Силы упругости. Закон Гука» —
Силы трения —
Примеры решения задач по теме «Силы трения» —
Примеры решения задач по теме «Силы трения» (продолжение) —
Источник
2017-05-21 ![]()
К вертикальной невесомой пружине, верхний конец которой закреплен, подвешен груз массы $m = 0,1 кг$. Жесткость пружины $k = 40 Н/м$. Определить период вертикальных колебаний системы, которые возникнут, если вывести груз из положения равновесия. Определить амплитуду колебаний и начальную фазу, если в момент $t = 0$ груз оттянуть вниз на расстояние $x_{1} = 10 см$ и сообщить ему начальную скорость $v_{1} = 3,5 м/с$, направленную вниз (вверх).
Решение:
Задача практически состоит из двух самостоятельных частей. Анализ ее и решение также будут содержать легко прослеживаемые две части.
Период колебаний можно определить только в случае, если груз, движущийся поступательно, совершает гармонические колебания. Это значит, что ускорение груза должно быть прямо пропорционально его смещению от положения равновесия и направлено в противоположную сторону.

В процессе движения на груз действуют две силы: тяжести и упругости пружины. Сила упругости пружины однозначно определяется растяжением или сжатием пружины, т. е. смещением ее незакрепленного конца. Если ввести ось ОХ (рис.), то координата х груза равна смещению конца пружины от прямой $AA^{ prime}$ — уровня, на котором находился конец пружины в положении равновесия. Тогда полное растяжение пружины равно $x + s_{0}$ и сила упругости
$f_{x} = — k (x + s_{0})$, (1)
где $s_{0}$ — растяжение пружины, при котором груз находился в положении устойчивого равновесия, когда
$ks_{0} = mg$. (2)
Поскольку обе силы (тяжести и упругости) направлены вдоль оси ОХ, уравнение движения для груза можно записать сразу в скалярном виде:
$m ddot{x} = mg — k (x + s_{0})$.
Раскрывая скобки и учитывая равенство (2), получаем
$m ddot{x} = — kx$. (3)
Это и есть дифференциальное уравнение гармонического колебания, которое позволяет однозначно определить период колебаний.
Амплитуду колебаний $X_{0}$ можно найти, рассматривая изменение энергии при переходе из положения, в котором система находилась в момент $t = 0$, в положение, при котором $x = X_{0}$. Полная энергия системы состоит из кинетической энергии груза, потенциальной энергии груза в поле тяготения Земли (пружина невесома, поэтому речь идет только о грузе) и потенциальной энергии упругой деформации. Поскольку диссипативных сил нет и никакие внешние силы на систему груз—пружина не действуют, полная энергия системы при рассматриваемом переходе остается постоянной:
$Delta K + Delta U_{тяг} + Delta U_{упр} = 0$. (4)
После определения амплитуды колебаний начальную фазу $alpha_{0}$ можно найти, если выразить координату $x$ и скорость $v_{x}$ как функции времени и приравнять эти выражения при $t = 0$ значениям $x_{1}$ и $v_{1x}$, данным в условии задачи.
Уравнение (3) показывает, что тело заданной массы совершает гармонические колебания относительно положения равновесия с циклической частотой $omega = sqrt{k/m}$ и периодом $T = 2 pi sqrt{ m/k} = 0,31 с$.
Найдем каждое из слагаемых, входящих в уравнение (4). В начальном положении ($t = 0$), как следует из условия задачи, $x = x_{1}, v_{x} = v_{1x}$. В конечном положении $x = X_{0}, v_{x} = 0$. Следовательно, при этом переходе
$Delta K = — mv_{1}^{2}/2, Delta U_{тяг} = — mg (X_{0} — x_{1})$, (5)
$Delta U_{упр} = k (X_{0} + s_{0})^{2}/2 — k(x_{1} + s_{0})^{2}/2$.
Выражение потенциальной энергии деформации объясняется тем, что растяжение пружины при любом положении тела больше, чем его координата $x$ (для $x > 0$) на $s_{0}$.
Прежде чем подставлять выражения (5) в (4), рассмотрим отдельно изменение потенциальной энергии системы:
$Delta U_{тяг} + Delta U_{упр} = -mg (X_{0} — x_{1}) + kX_{0}^{2} /2 — kx_{1}^{2} /2 + ks_{0} (X_{0} — x_{1})$
(члены, содержащие $s_{0}^{2}$, взаимно уничтожаются). Учитывая равенство (2), получаем
$Delta U = Delta U_{тяг} + Delta U_{упр} = kX_{0}^{2}/2 — kx_{1}^{2}/2$. (6)
Можно показать, что найденное изменение потенциальной энергии равно взятой с обратным знаком работе результирующей силы при переходе тела от $x = x_{1}$, к $x = X_{0}$:
$f_{x ~ рез} = — kx, dA = — kx dx$,
$Delta U = -A = int_{x_{1}}^{X_{0}} kx dx = kX_{0}^{2}/2 — kx_{1}^{2}/2$.
Такой результат справедлив для любого гармонического осциллятора: изменение потенциальной энергии равно взятой с обратным знаком работе результирующей квазиупругой силы.
Подставив первое из выражений (5) и (6) в (4), получим
$- mv_{1}^{2}/2 + kX_{0}^{2}/2 — kx_{1}^{2}/2 = 0$,
откуда
$X_{0} = sqrt{mv_{1}^{2} / k + x_{1}^{2}} = 0,2 м$.
Запишем теперь выражения для $x(t)$ и $v_{x}(t)$:
$x = X_{0} sin ( omega t + alpha_{0})$,
$v_{x} = dot{x} = X_{0} omega cos ( omega t + alpha_{0})$.
При $t = 0$
$x(0) = X_{0} sin alpha_{0} = x_{1}, v_{x}(0) = X_{0} omega cos alpha_{0} = pm v_{1}$. (7)
Следовательно, $alpha_{0} = arcsin (x_{1}/X_{0}) = pi /6$ (или $5 pi/6$). Знак «+» в выражении (7) соответствует направлению скорости $v_{1}$ вниз. В этом случае $X_{0} omega cos alpha_{0} > 0$. Следовательно, $alpha_{0} = pi /6$. Если скорость $v_{1}$ направлена вверх, то $v_{1x} = — v_{1}, X_{0} omega cos alpha_{0}
Источник
Задача по физике — 5153
По свежему снегу прошёл снегоход массой 375 кг с площадью опорной поверхности гусениц 0,75 $м^{2}$. По следу снегохода идёт человек массой 80 кг. Площадь одной подошвы валенок 250 $см^{2}$. Будет ли человек проваливаться в снег?
Подробнее
Задача по физике — 5156
На трёх пружинах, прикреплённых к потолку, горизонтально висит однородный тонкий стержень (см. рис.). Расстояние между первой и второй пружинами $L_{12} = 10 см$, расстояние между второй и третьей пружинами $L_{23} = 30 см$. Коэффициенты жёсткости пружин известны: $k_{1} = 1 кН/м, k_{2} = 2 кН/м, k_{3} = 1 кН/м$. Растяжения первой и третьей пружин равны $Delta x_{1} = 5 см$ и $Delta x_{3} = 10 см$. Найти растяжение второй пружины $Delta x_{2}$.

Подробнее
Задача по физике — 5157
Тело поднимают с помощью наклонной плоскости и системы блоков (см. рис.). Какую минимальную силу $F$ нужно приложить, чтобы поднять тело массы $m$? Высота наклонной плоскости равна $H$, длина $L$. Блоки невесомые. Трением пренебречь.

Подробнее
Задача по физике — 5158
К потолку прикреплена конструкция, состоящая из двух пружин и двух маленьких чашек A и B (см. рис.). Расстояние от пола до потолка равно 2 м. Жёсткости пружин равны $k_{1} = 15 Н/м$ и $k_{2} = 30 Н/м$. Длины нерастянутых пружин одинаковы и равны 30 см. Масса чашки A равна $m = 100 г$, чашка B невесома. Груз какой массы надо положить в чашку A, чтобы чашка B достала до пола? Какой груз надо положить в чашку B, чтобы она достала до пола (чашка A при этом пуста)?

Подробнее
Задача по физике — 5179
Две одинаковые лодки, связанные между собой лёгким канатом, покоились на поверхности воды на расстоянии $L$ друг от друга. В некоторый момент времени матросы на одной из лодок стали тянуть канат, и лодка начала двигаться с постоянным ускорением $a$. Через какое время лодки столкнутся?
Подробнее
Задача по физике — 5183
B системе, изображённой на рис., пружины имеют жёсткости $k_{1} = 100 Н/м$ и $k_{2} = 200 Н/м$. К нижнему блоку подвешивают груз массой $M = 8 кг$. Система приходит в равновесие. На сколько сместился нижний блок? Пружины, нити и блоки невесомы. Нити нерастяжимы.

Подробнее
Задача по физике — 5184
Труба, сечение которой является квадратом со стороной $a = 20 см$, закрыта поршнем (см. рис.). К трубе присоединена трубка. Часть трубы, находящаяся справа от поршня, полностью заполнена водой, уровень воды в трубке равен $h = 15 см$. Силу какой величины и направления надо прикладывать к поршню, чтобы удерживать его в равновесии? Трение отсутствует.

Подробнее
Задача по физике — 5186
Какова минимальная площадь присоски, с помощью которой можно прикрепить пробковый брусок массы $m$ к горизонтальной поверхности на глубине $h$ под водой (рис.)? Плотность пробки $rho$, плотность воды $rho_{0}$, атмосферное давление $p_{a}$.

Подробнее
Задача по физике — 5190
Грузы, имеющие массы $M$ и $m$ ($M > m$) при помощи невесомой нерастяжимой нити подвешены на блоке, как показано на рис. С каким минимальным ускорением нужно двигать блок в вертикальном направлении, чтобы ускорения грузов (относительно земли) были направлены в одну сторону? Грузы двигаются по вертикали. Ускорение свободного падения равно $g$. Сопротивлением воздуха пренебречь.

Подробнее
Задача по физике — 5191
По горизонтальной плоскости скользит без трения точечная шайба массы $m$ (см. рис.). Скорость шайбы $v$. Перпендикулярно направлению движения шайбы движется лента транспортёра с такой же по модулю скоростью $V$. Сила трения между поверхностями шайбы и транспортёра $F$. Какой должна быть ширина транспортёра $H$ для того, чтобы шайба переехала через него?

Подробнее
Задача по физике — 5192
Две невесомых пружины с коэффициентами жёсткости $k_{1} = 24 Н/м$ и $k_{2} = 12 Н/м$ и лёгкая шайба, скользящая вдоль стержня без трения, соединены вместе, как показано на рис. К свободному концу пружины прикладывают такую силу $F(t)$, что он движется вправо с постоянной скоростью $V = 0,2 м/с$. Найдите скорость шайбы. Постройте график зависимости силы $F(t)$ от времени.

Подробнее
Задача по физике — 5193
Лыжник на водных лыжах движется по прямой с постоянной скоростью. Сила натяжения каната, за который держится лыжник равна $T$, а масса лыжника равна $m$. Найти угол под которым наклонены лыжи к зеркалу воды.
Подробнее
Задача по физике — 5194
К концам невесомой нерастяжимой нити, перекинутой через блок (см. рис.), прикреплены грузы с массами $m_{1}$ и $m_{2}$, причём $m_{1} > m_{2}$ В начальный момент грузы неподвижны, и расстояние между ними равно $h$. Через какое время грузы окажутся на одинаковом расстоянии от блока?

Подробнее
Задача по физике — 5195
Сосуд с водой уравновешен через блок грузом массы $M$. Система устроена так (см. рис.), что нити, проходящие через блок, вертикальны. Определить силу натяжения нити. Считать, что груз лежит на дне сосуда. Масса сосуда вместе с водой — $m$, ускорение свободного падения — $g$.

Подробнее
Задача по физике — 5196
Сосуд имеет снизу сливное отверстие, герметично заткнутое пробкой. К пробке привязана нерастяжимая нить длиной $L = 10 см$. Другой конец нити привязан к бруску кубической формы, изготовленного из материала, имеющего плотность $rho_{1} = 102 кг/м^{3}$. В сосуд медленно наливают воду. Минимальный размер бруска, при котором пробка вытаскивается из отверстия, составляет $a = 10 см$. Чему равна площадь пробки? Массой пробки пренебречь. Трением между пробкой и стенками сосуда пренебречь, пробка над краями отверстия не выступает.
Подробнее
Источник
Глава 3. Силы в механике
При решении задач по этой теме надо иметь в виду, что закон Гука справедлив только при упругих деформациях тел. Сила упругости не зависит от того, какая происходит деформация: сжатия или растяжения, она одинакова при одинаковых Δl. Кроме этого, считается, что сила упругости вдоль всей пружины одинакова, так как масса пружины обычно не учитывается.
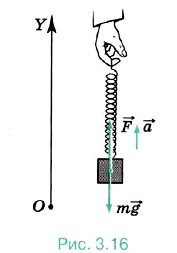
Задача 1. При помощи пружинного динамометра поднимают с ускорением а = 2,5 м/с2, направленным вверх, груз массой m = 2 кг. Определите модуль удлинения пружины динамометра, если её жёсткость k = 1000 Н/м.
Р е ш е н и е. Согласно закону Гука, выражающему связь между модулем внешней силы 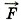 , вызывающей растяжение пружины, и её удлинением, имеем F = kΔl. Отсюда
, вызывающей растяжение пружины, и её удлинением, имеем F = kΔl. Отсюда 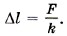
Для нахождения силы  воспользуемся вторым законом Ньютона. На груз, кроме силы тяжести m
воспользуемся вторым законом Ньютона. На груз, кроме силы тяжести m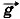 , действует сила упругости пружины, равная по модулю F и направленная вертикально вверх. Согласно второму закону Ньютона m
, действует сила упругости пружины, равная по модулю F и направленная вертикально вверх. Согласно второму закону Ньютона m = F + m
= F + m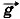 .
.
Направим ось OY вертикально вверх так, чтобы пружина была расположена вдоль этой оси (рис. 3.16). В проекции на ось OY второй закон Ньютона можно записать в виде mау = Fy + mgy.
Так как ау = a, gy = -g и Fy = F, то F = mа + mg = m(а + g).
Следовательно,
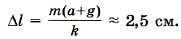
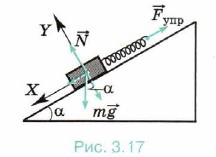
Задача 2. Определите, как изменяется сила натяжения пружины, прикреплённой к бруску массой m = 5 кг, находящемуся неподвижно на наклонной поверхности, при изменении угла наклона от 30° до 60°. Трение не учитывайте.
Р е ш е н и е. На брусок действуют сила тяжести, сила натяжения пружины и сила реакции опоры (рис. 3.17).
Условие равновесия бруска: m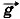 +
+ 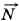 +
+ 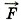 yпp = 0.
yпp = 0.
Запишем это условие в проекциях на оси ОХ и OY: 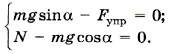
Из первого уравнения системы получим Fyпp = mg sinα.
При изменении угла наклона изменение силы упругости найдём из выражения ΔFyпp = mg(sinα2 — sinα1) = 5 • 10 • (0,866 — 0,5) (Н) = 18,3 Н.
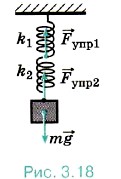
Задача 3. К потолку подвешены последовательно две невесомые пружины жёсткостями 60 Н/м и 40 Н/м. К нижнему концу второй пружины прикреплён груз массой 0,1 кг. Определите жёсткость воображаемой пружины, удлинение которой было бы таким же, как и двух пружин при подвешивании к ней такого же груза (эффективную жёсткость).
Р е ш е н и е. Так как весом пружин можно пренебречь, то очевидно, что силы натяжения пружин равны (рис. 3.18). Тогда согласно закону Гука
Fynp1 = Fупр2; k1x1 = k2х2. (1)
На подвешенный груз действуют две силы — сила тяжести и сила натяжения второй пружины.
Условие равновесия груза запишем в виде mg = k2х2.
Из этого уравнения найдём удлинение 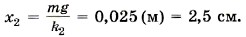
Подставив выражение для х2 в уравнение (1), получим для удлинения 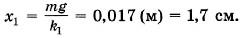
Определим теперь эффективную жёсткость. Запишем закон Гука для воображаемой пружины:
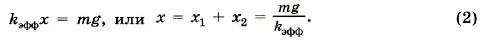
Подставив в формулу (2) выражения для удлинений x1 и х2 пружин, получим 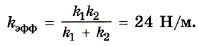
Для эффективной жёсткости получим выражение 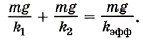
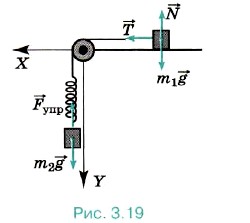
Задача 4. Через блок, закреплённый у края стола, перекинута нерастяжимая нить, к концам которой привязаны брусок массой m1 = 1 кг, находящийся на горизонтальной поверхности стола, и пружина жёсткостью k = 50 Н/м, расположенная вертикально. Ко второму концу пружины привязана гиря массой m2 = 200 г (рис. 3.19). Определите удлинение пружины при движении тел. Силу трения, массы пружины, блока и нити не учитывайте.
Р е ш е н и е. На брусок действуют сила тяжести, сила реакции опоры и сила натяжения нити.
На гирю действуют сила тяжести и сила натяжения пружины.
Согласно второму закону Ньютона для бруска и гири запишем:
m1 1 = m1
1 = m1 +
+ 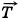 +
+ 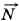 ;
;
m2 2 = m
2 = m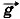 +
+ 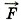 упр.
упр.
В проекциях на выбранные оси координат запишем: на ось ОХ: m1а1 = Т;
на ось OY: 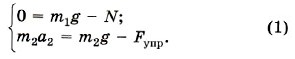
Так как нить нерастяжима, то модули ускорений равны: а1 = а2 = а.
В силу условия малых масс пружины, нити и блока можно записать: T2 = Fупр и Т1 = Т2 = Т.
Учтя последние равенства, систему уравнений (1) запишем в виде
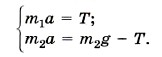
Выразив ускорение из первого уравнения системы и подставив его во второе, получим 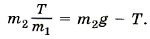 Из этого уравнения найдём силу натяжения нити:
Из этого уравнения найдём силу натяжения нити: 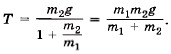
Так как согласно закону Гука Fупр = kx, то 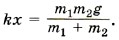
Тогда удлинение пружины 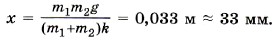
Задачи для самостоятельного решения
1. К динамометру привязан груз массой 2 кг. Динамометр с грузом опускают с ускорением 3 м/с2. Жёсткость пружины 103 Н/м. Определите модуль растяжения пружины динамометра.
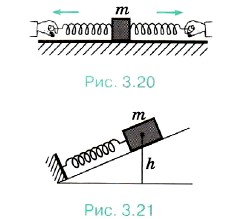
2. К бруску массой 1 кг, находящемуся на гладкой горизонтальной поверхности, прикреплены две пружины (рис. 3.20). Жёсткость правой пружины 2 • 103 Н/м, левой — в 2 раза меньше. Чему равно отношение удлинений пружин в случае, когда брусок неподвижен?
3. Ящик массой 100 кг удерживается на наклонной плоскости на высоте 0,5 м закреплённой у основания пружиной, жёсткость которой равна 104 Н/м (рис. 3.21). Определите длину пружины в недеформированном сотоянии. Угол у основания наклонной плоскости равен 30°. Трением можно пренебречь.
4. К нижнему концу лёгкой пружины подвешены связанные невесомой нитью грузы: верхний массой m1 = 0,5 кг и нижний массой m2 = 0,2 кг. Нить, соединяющую грузы, пережигают. Определите проекцию ускорения на направленную вниз ось OY, с которым начнёт двигаться верхний груз.
Источник
