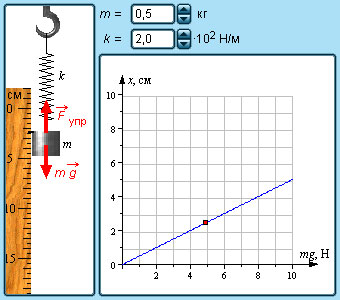
Растяжение пружины с грузом
Главная
Онлайн учебники
База репетиторов России
Тренажеры по физике
Подготовка к ЕГЭ 2017 онлайн
Глава 1. Механика
Силы в природе
1.12. Сила упругости. Закон Гука
При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.
Простейшим видом деформации являются деформации растяжения и сжатия (рис. 1.12.1).
| Рисунок 1.12.1. Деформация растяжения ( x > 0 ) и сжатия ( x < 0 ). Внешняя сила |
При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:
Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жесткостью тела. В системе СИ жесткость измеряется в ньютонах на метр (Н/м). Коэффициент жесткости зависит от формы и размеров тела, а также от материала. В физике закон Гука для деформации растяжения или сжатия принято записывать в другой форме. Отношение ε = x / l называется относительной деформацией, а отношение σ = F / S = –Fупр / S, где S – площадь поперечного сечения деформированного тела, называется напряжением. Тогда закон Гука можно сформулировать так: относительная деформация ε пропорциональна напряжению σ:
Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Модуль Юнга различных материалов меняется в широких пределах. Для стали, например, E ≈ 2·1011 Н/м2, а для резины E ≈ 2·106 Н/м2, т. е. на пять порядков меньше.
Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рис. 1.12.2).
| Рисунок 1.12.2. Деформация изгиба. |
Упругую силу действующую на тело со стороны опоры (или подвеса), называют силой реакции опоры. При соприкосновении тел сила реакции опоры направлена перпендикулярно поверхности соприкосновения. Поэтому ее часто называют силой нормального давления. Если тело лежит на горизонтальном неподвижном столе, сила реакции опоры направлена вертикально вверх и уравновешивает силу тяжести: Сила с которой тело действует на стол, называется весом тела.
В технике часто применяются спиралеобразные пружины (рис. 1.12.3). При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром. Следует иметь в виду, что при растяжении или сжатии пружины в ее витках возникают сложные деформации кручения и изгиба.
В отличие от пружин и некоторых эластичных материалов (резина) деформация растяжения или сжатия упругих стержней (или проволок) подчиняются линейному закону Гука в очень узких пределах. Для металлов относительная деформация ε = x / l не должна превышать 1 %. При больших деформациях возникают необратимые явления (текучесть) и разрушение материала.
 |
Модель. |
Источник
Анонимный вопрос · 2 декабря 2018
533
На динамометре есть шкала и стрелка, которая показывает силу воздействия. Если гвоорить о формуле, то F = mg, где F — сила (ньютоны), воздействующая на прибор, m — масса груза (кг), а g — ускорение свободного падения, для земли равное 9,8. Из формулы следует, что 100 г грузик будет действовать с силой примерно 1 ньютон.
Каким образом можно вычислить энергию деформации груза и сваи?
Представим, что в лабораторной работе необходимо вычислить энергию деформации сваи в процессе ее забивки в грунт при помощи груза. При падении груза потенциальная энергия переходит в кинетическую. Вот и обозначаем скорость груза перед ударом v1, а его массу — m1. Есть еще одна величина – Н – высота груза над забиваемой сваей. Вот практически готово условие задачи. Применим для вычислений два уравнения: m1 gH = m1v12 2. v= √2gH.
Понимаем, что сталкивающие тела постепенно деформируются, поэтому возникают упругие силы и силы трения. В свае и грузе возбуждаются колебания и волны. Значит, свая и груз движутся как единое целое с массой m1 + m2 и с общей скоростью v. Общую скорость груза и сваи сразу после удара можно найти, применяя закон сохранения импульса к системе «груз–свая». Согласно закону сохранения импульса, делаем вычисления m1v1 = (m1 + m2)v.
Формулу преобразовываем в V=m1m1+m2 X √2gH.
Появляется новый параметр – средняя сила сопротивления при забивки сваи в грунт — Fср.
При этом сила сопротивления грунта совершает работу, равную, где S – смещение сваи с грузом в грунте.Так как сила сопротивления грунта Fср и смещение направлены по одной прямой, но в противоположные стороны, то cos a = -1. Тогда А = —Fср × S .Эта работа равна изменению энергии системы «груз–свая–Земля», т.е.-Fср×S = W2 – W1 или Fср×S = W1 — W2, где W1 и W2 – механическая энергия системы в начале движения и в момент остановки, соответственно.
Вес человека 500Н он встал на пружинные весы на лестнице эскалатора, движущейся равномерно вниз со скоростью 0,5 м/с. Какими были показания весов?
физик-теоретик в прошлом, дауншифтер и журналист в настоящем, живу в Германии
Раз человек движется равномерно и прямолинейно, то его система отсчета инерциальна и нет никаких «сил инерции».
Соответственно, его вес (сила давления на весы) так и остался Р=500 Н. Масса М=Р/g, где g=9,8 м/с^2 — ускорение свободного падения. Весы показывают вес не в Ньютонах, а в кгс (килограмм-сила, внесистемная единица), а количественно вес в этих единицах равен массе в килограммах. То есть, весы покажут около 51 кг (на самом деле они покажут вес в 51 кгс).
Ну, или можно сразу пересчитать Ньютоны в кгс, зная, что 1 кгс = 9,8 Н. Тогда Р= (500 Н / 9,8 Н)×1 кгс = 51 кгс и именно это покажут весы. Даже если на них будет написано «кг», а не «кгс». Потому что массу (в килограммах) они на самом деле не измеряют, а измеряют вес (силу давления).
Как пользоваться динамометром сжатия механическим?
Динамометры, как известно, измеряют силу. И хотя все шире переход на электронику в самых различных областях, механические динамометры все еще очень даже в ходу. В основе механизма действия — пружина или рычаг, на которые воздействует некая сжимающая сила, а результат выводится на табло. В быту почти все мы сталкивались с простыми пружинными динамометрами, которые сжимают кулаком для определения силы кисти. В промышленности принципы аналогичные, только в больших масштабах. Например, при испытании прессов упругий элемент принимает на себя нагрузку сжатия и передает ее значение на циферблат.
На каком расстоянии от поверхности земли сила притяжения космического корабля уменьшается в 121 раз?
Книги, звери и еда — это хобби навсегда.
Сила взаимного притяжения пропорциональна произведению масс взаимодействующих тел и обратно пропорциональна квадрату расстояния между центрами их масс:
F=G*m1*m2/r^2
Тогда F2/F1=1/121=(G*m1*m2/r2^2)/(G*m1*m2/r1^2)=r1^2/r1^2
Поскольку начальное расстояние между кораблем и центром Земли равно радиусу Земли r1=R=6371 км = 6.371*10^6 м, то
F2/F1=R^2/(R+h)^2=1/121, тогда R/(R+h)=1/11, 11*R=R+h и h=10*R=63710 км.
Почему в теоретической механике в качестве букв для обозначения координатных осей иногда используют кси, эту и дзету?
Выпускник МФТИ, аспирант Сколтеха
Дело в том, что аналогами (xi, eta, zeta) в английском алфавите являются (x, e, z). В идеале это было бы (x, y, z), но в греческом языке нет аналога буквы y. Этим и объясняется широкое использование таких обозначений как в теоретической механике, так и во многих математических трудах.
Источник
Можно не знать закон Ома и сидеть дома. Но если не знаешь закон Гука – лучше тоже не выходить. Особенно, если идешь на экзамен по физике.
Здесь устраняем пробелы в знаниях и разбираемся, как решать задачи на силу упругости и применение закона Гука. А за полезной рассылкой для студентов добро пожаловать на наш телеграм-канал.
Сила упругости и закон Гука: определения
Сила упругости – сила, препятствующая деформациям и стремящаяся восстановить первоначальные форму и размеры тела.
Примеры действия силы упругости:
- пружины сжимаются и разжимаются в матрасе;
- мокрое белье колышется на натянутой веревке;
- лучник натягивает тетиву, чтобы выпустить стрелу.
Простейшие деформации – деформации растяжения и сжатия.
Закон Гука:
Деформация, возникающая в упругом теле под действием внешней силы, пропорциональна величине этой силы.
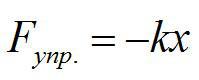
Коэффициент k – жесткость материала.
Есть и другая формулировка закона Гука. Введем понятие относительной деформации «эпсилон» и напряжения материала «сигма»:
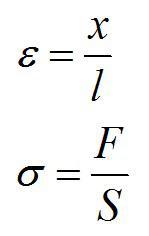
S – площадь поперечного сечения деформируемого тела. Тогда закон Гука запишется так: относительная деформация пропорциональна напряжению.
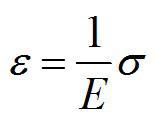
Здесь Е – модуль Юнга, зависящий от свойств материала.
Закон Гука был экспериментально открыт в 1660 году англичанином Робертом Гуком.
Вопросы на силу упругости и закон Гука
Вопрос 1. Какие бывают деформации?
Ответ. Помимо простейших деформаций растяжения и сжатия, бывают сложные деформации кручения и изгиба. Также разделяют обратимые и необратимые деформации.
Вопрос 2. В каких случаях закон Гука справедлив для упругих стержней?
Ответ. Для упругих стержней (в отличие от эластичных тел) закон Гука можно применять при малых деформациях, когда величина эпсилон не превышает 1%. При больших деформациях возникают явления текучести и необратимого разрушения материала.
Вопрос 3. Как направлена сила упругости?
Ответ. Сила упругости направлена в сторону, противоположную направлению перемещения частиц тела при деформации.
Вопрос 4. Какую природу имеет сила упругости?
Ответ. Сила упругости, как и сила трения – электромагнитная сила. Она возникает вследствие взаимодействия между частицами деформируемого тела.
Вопрос 5. От чего зависит коэффициент жесткости k? Модуль Юнга E?
Ответ. Коэффициент жесткости зависит от материала тела, а также его формы и размеров. Модуль Юнга зависит только от свойств материала тела.
Задачи на силу упругости и закон Гука с решениями
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Задача №1. Расчет силы упругости
Условие
Один конец проволоки жестко закреплен. С какой силой нужно тянуть за второй конец, чтобы растянуть проволоку на 5 мм? Жесткость проволоки известна и равна 2*10^6 Н/м2.
Решение
Запишем закон Гука:
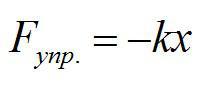
По третьему закону Ньютона:
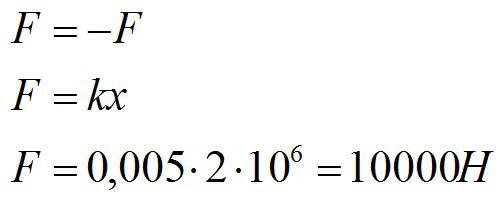
Ответ: 10 кН.
Задача №2. Нахождение жесткости пружины
Условие
Пружину, жесткость которой 100 Н/м, разрезали на две части. Чему равна жесткость каждой пружины?
Решение
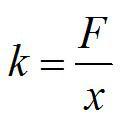
По определению, жесткость обратно-пропорциональна длине. При одинаковой силе F неразрезанная пружина растянется на х, а разрезанная – на x1=x/2.
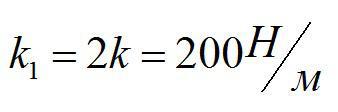
Ответ: 200 Н/м
При растяжении пружины в ее витках возникают сложные деформации кручения и изгиба, однако мы не учитываем их при решении задач.
Задача №3. Нахождение ускорения тела
Условие
Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины, которая при движении растянулась на 2 см. Жесткость пружины 200 Н/м. Определить ускорение, с которым движется тело.
Решение
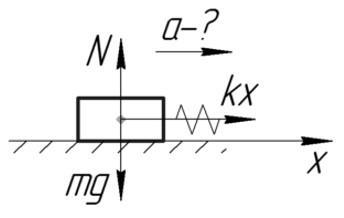
За силу, которая приложена к телу и заставляет его двигаться, можно принять силу упругости. По второму закону Ньютона и по закону Гука:
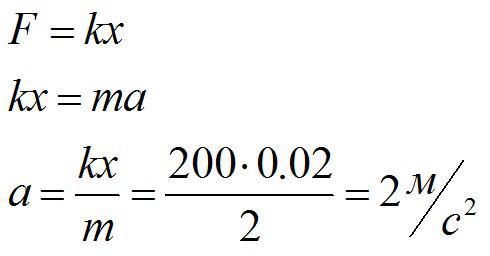
Ответ: 2 м/с^2.
Задача №4. Нахождение жесткости пружины по графику
Условие
На графике изображена зависимость модуля силы упругости от удлинения пружины. Найти жесткость пружины.
Решение
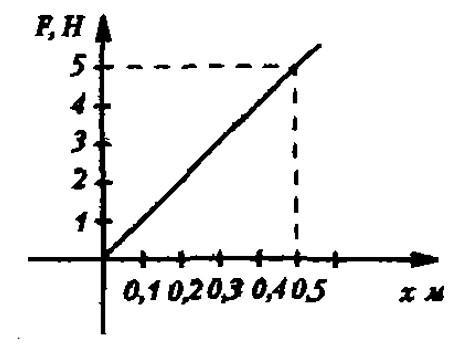
Вспоминаем, что жесткость равна отношению силы и удлинения. Представленная зависимость – линейная. В любой точке прямой отношение ординаты F и абсциссы х дает результат 10 Н/м.
Ответ: k=10 Н/м.
Задача №5. Определение энергии деформации
Условие
Для сжатия пружины на х1=2 см надо приложить силу 10 Н. Определить энергию упругой деформации пружины при сжатии на х2=4 см из недеформированного состояния.
Решение
Энергия сжатой пружины равна:
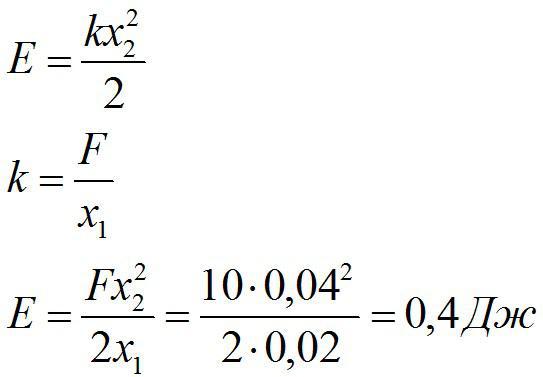
Ответ: 0,4 Дж.
Нужна помощь в решении задач? Обращайтесь за ней в профессиональный студенческий сервис.
Автор
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Источник
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Сила упругости — это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Силы, возникающие при пластических деформациях, не относятся к силам упругости.
Понятие о деформациях
Деформация — это изменение формы и размеров тела.
К деформациям относятся: растяжение, сжатие, кручение, сдвиг, изгиб.
Деформации бывают упругими и пластическими.
Закон Гука
Абсолютная величина силы упругости прямо пропорциональна величине деформации. В частности, для пружины, сжатой или растянутой на величину (displaystyle x) (разница между крайними положениями), сила упругости задается формулой [F=kx] где (displaystyle k) — коэффициент жесткости пружины.
Единицы измерения коэффициента жесткости: (k=)[Н/м].
Закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела.
Кубик массой (M = 2) кг, сжатый с боков пружинами, покоится на гладком горизонтальном столе. Первая пружина сжата на 2 см, а вторая сжата на 6 см. Жёсткость первой пружины (k_1 = 1200) Н/м. Чему равна жёсткость второй пружины (k_2)? Ответ выразите в Н/м.
По второму закону Ньютона силы упругости пружин будут уравновешивать друг друга, следовательно: [k_1Delta x_1=k_2Delta x_2] где (Delta x_1) и (Delta x_2) – сжатие первой и второй пружины соответственно.
Откуда жесткость второй пружины [k_2=dfrac{k_1 Delta x_1}{Delta x_2}= dfrac{1200text{ Н/м}cdot 2text{ см}}{6text{ см}}=400text{ Н/м}]
Ответ: 400
На штативе закреплён школьный динамометр. К нему подвесили груз массой 0,1 кг. Пружина динамометра при этом удлинилась на 2,5 см. Чему будет равно удлинение пружины, если масса груза увеличится втрое? (Ответ дайте в сантиметрах)
Согласно закону Гука [F=kDelta x] где k – жесткость пружины, ( Delta x) – удлинение пружины.
Найдем жесткость пружины, зная, что ( Delta x) = 2,5 см = 0,025 м при приложении силы, равно ( F=m_1g=0,1cdot 10=1text{ H} ): [k=dfrac{F}{Delta x}=dfrac{1}{0,025}=40text{ H/кг}] Если массу груза увеличить в 3 раза, то есть, (m_2=0,3) кг, то удлинение пружины будет равно: [Delta x=dfrac{F}{k}=dfrac{m_2g}{k}=dfrac{3cdot0,1cdot10text{ H}}{40text{ H/кг}}=0,075text{ м}=7,5text{ см}]
Ответ: 7,5
К системе из кубика массой M = 3 кг и двух пружин приложена постоянная горизонтальная сила F величиной 20 Н (см. рисунок). Между кубиком и опорой трения нет. Система покоится. Жёсткость первой пружины (k_1 = 400 text{ Н/м}). Жёсткость второй пружины (k_2 = 800 text{ Н/м}). Каково удлинение первой пружины? (Ответ дайте в сантиметрах)
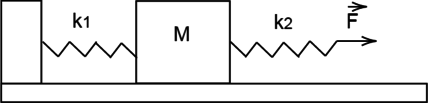
Согласно закону Гука удлинение (Delta x) пружины связано с ее жесткостью k и приложенной к ней силе F выражением (F=kDelta x). На первую пружину действует такая же сила F, что и на вторую, так как трения между кубиком и опорой нет. То, что первая пружина соединена со второй через кубик, здесь не имеет никакого значения, соответственно удлинение первой пружины – это величина, равная: [Delta x=dfrac{F}{k_1}=dfrac{20text{ H}}{400text{ H/м}}=0,05 text{ м}=5 text{ см}]
Ответ: 5
Определите силу, под действием которой пружина жёсткостью 200 Н/см удлинится на 5 мм.
Согласно закону Гука ( F=kDelta x ), где k – жесткость пружины, ( Delta x) – удлинение пружины, получаем: [F=kDelta x=(dfrac{200}{0,01})text{H/м}cdot(5cdot10^{-3})text{м}=100text{ H}]
Ответ: 100
Пружина одним концом прикреплена к неподвижной опоре, к другому концу приложили силу равную 1500 Н, при этом пружина растянулась на 0,2 м. Определите жесткость данной пружины. Ответ дать в Н/м.
После растяжения, пружина покоится и на неё действуют 2 силы направленные в противоположные направления: (F_{text{упр}}) – сила упругости и F – приложенная сила.
Тогда по первому закону Ньютона: [F_{text{упр}}=F] По закону Гука: [F_{text{упр}}=kx] Приравниваем эти формулы: [F=kx] Тогда [k=frac{F}{x}=frac{1500}{0,2}=7500 text{ Н/м}]
Ответ: 7500
К потолку прикреплены одним концом две пружины с одинаковой жесткостью. За другой конец первую пружину растягивают с силой (F_{text{1}}), которая в 2,5 раза больше силы (F_{text{2}}), растягивающей вторую пружину. При этом вторая пружина растянулась на 0,4 м. Насколько растянулась первая пружина? Ответ дать в метрах.
После растяжения обе пружины находятся в покое и на них, кроме данных сил действует сила упругости. Тогда по первому закону Ньютона: [F_{text{упр1}}=F_{text{1}}] [F_{text{упр2}}=F_{text{2}}] где (F_{text{упр1}}) – сила упругости, действующая на первую пружина, (F_{text{упр2}}) – на вторую.
По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [kx_{1}=F_{1}quad(1)] [kx_{2}=F_{text{2}}quad(2)] где (x_{1}) – удлинение первой пружины, (x_{2}) – второй. Разделим (1) на (2), получится: [frac{x_{1}}{x_{2}}=frac{F_{text{1}}}{F_{text{2}}}Rightarrow x_{1}=dfrac{F_{text{1}}x_{2}}{F_{text{2}}}=2,5cdot0,4=1text{ м}]
Ответ: 1
К грузу массой (m) аккуратно подвесили другой груз массой (M), при этом пружина с жесткостью 1200 Н/м удлинилась так, как показано на рисунке. Найдите массу (M). Ускорение свободного падения считать равным 10 м/(c^{2}). Ответ дать в кг.
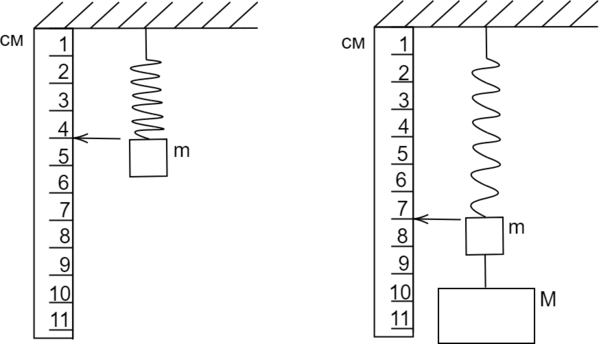
Рассмотрим ситуацию до подвешивания груза: система тел “груз и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg=F_{text{упр}1}] Рассмотрим ситуацию после подвешивания груза: систама тел “2 груза и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg+Mg=F_{text{упр2}}] По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [mg=kx_{1}quad(1)] [mg+Mg=kx_{2}quad(2)] Вычтем (1) из (2), получится: [Mg=k(x_{2}-x_{1})Rightarrow M=dfrac{k(x_{2}-x_{1})}{g}=frac{1200cdot0,03}{10}=3,6text{ кг}]
Ответ: 3,6
Источник
