Растяжение пружины формула физика
Главная
Онлайн учебники
База репетиторов России
Тренажеры по физике
Подготовка к ЕГЭ 2017 онлайн
Глава 1. Механика
Силы в природе
1.12. Сила упругости. Закон Гука
При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.
Простейшим видом деформации являются деформации растяжения и сжатия (рис. 1.12.1).
| Рисунок 1.12.1. Деформация растяжения ( x > 0 ) и сжатия ( x < 0 ). Внешняя сила |
При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:
Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жесткостью тела. В системе СИ жесткость измеряется в ньютонах на метр (Н/м). Коэффициент жесткости зависит от формы и размеров тела, а также от материала. В физике закон Гука для деформации растяжения или сжатия принято записывать в другой форме. Отношение ε = x / l называется относительной деформацией, а отношение σ = F / S = –Fупр / S, где S – площадь поперечного сечения деформированного тела, называется напряжением. Тогда закон Гука можно сформулировать так: относительная деформация ε пропорциональна напряжению σ:
Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Модуль Юнга различных материалов меняется в широких пределах. Для стали, например, E ≈ 2·1011 Н/м2, а для резины E ≈ 2·106 Н/м2, т. е. на пять порядков меньше.
Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рис. 1.12.2).
| Рисунок 1.12.2. Деформация изгиба. |
Упругую силу действующую на тело со стороны опоры (или подвеса), называют силой реакции опоры. При соприкосновении тел сила реакции опоры направлена перпендикулярно поверхности соприкосновения. Поэтому ее часто называют силой нормального давления. Если тело лежит на горизонтальном неподвижном столе, сила реакции опоры направлена вертикально вверх и уравновешивает силу тяжести: Сила с которой тело действует на стол, называется весом тела.
В технике часто применяются спиралеобразные пружины (рис. 1.12.3). При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром. Следует иметь в виду, что при растяжении или сжатии пружины в ее витках возникают сложные деформации кручения и изгиба.
В отличие от пружин и некоторых эластичных материалов (резина) деформация растяжения или сжатия упругих стержней (или проволок) подчиняются линейному закону Гука в очень узких пределах. Для металлов относительная деформация ε = x / l не должна превышать 1 %. При больших деформациях возникают необратимые явления (текучесть) и разрушение материала.
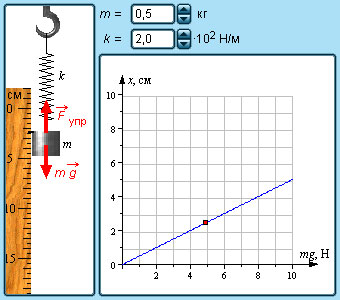 |
Модель. |
Источник
Определение и формула жесткости пружины
Определение
Силу, которая возникает в результате деформации тела и пытающаяся вернуть его в исходное состояние, называют силой упругости.
Чаще всего ее обозначают ${overline{F}}_{upr}$. Сила упругости появляется только при деформации тела и исчезает, если пропадает деформация. Если после снятия внешней нагрузки тело восстанавливает свои размеры и форму полностью, то такая деформация называется упругой.
Современник И. Ньютона Р. Гук установил зависимость силы упругости от величины деформации. Гук долго сомневался в справедливости своих выводов. В одной из своих книг он привел зашифрованную формулировку своего закона. Которая означала: «Ut tensio, sic vis» в переводе с латыни: каково растяжение, такова сила.
Рассмотрим пружину, на которую действует растягивающая сила ($overline{F}$), которая направлена вертикально вниз (рис.1).
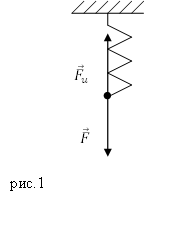
Силу $overline{F }$ назовем деформирующей силой. От воздействия деформирующей силы длина пружины увеличивается. В результате в пружине появляется сила упругости (${overline{F}}_u$), уравновешивающая силу $overline{F }$. Если деформация является небольшой и упругой, то удлинение пружины ($Delta l$) прямо пропорционально деформирующей силе:
[overline{F}=kDelta lleft(1right),]
где в коэффициент пропорциональности называется жесткостью пружины (коэффициентом упругости) $k$.
Жесткость (как свойство) — это характеристика упругих свойств тела, которое деформируют. Жесткость считают возможностью тела оказать противодействие внешней силе, способность сохранять свои геометрические параметры. Чем больше жесткость пружины, тем меньше она изменяет свою длину под воздействием заданной силы. Коэффициент жесткости — это основная характеристика жесткости (как свойства тела).
Коэффициент жесткости пружины зависит от материала, из которого сделана пружина и ее геометрических характеристик. Например, коэффициент жесткости витой цилиндрической пружины, которая намотана из проволоки круглого сечения, подвергаемая упругой деформации вдоль своей оси может быть вычислена как:
[k=frac{Gd^4}{8d^3_pn}left(2right),]
где $G$ — модуль сдвига (величина, зависящая от материала); $d$ — диаметр проволоки; $d_p$ — диаметр витка пружины; $n$ — количество витков пружины.
Единицей измерения коэффициента жесткости в Международной системе единиц (Си) является ньютон, деленный на метр:
[left[kright]=left[frac{F_{upr }}{x}right]=frac{left[F_{upr }right]}{left[xright]}=frac{Н}{м}.]
Коэффициент жесткости равен величине силы, которую следует приложить к пружине для изменения ее длины на единицу расстояния.
Формула жесткости соединений пружин
Пусть $N$ пружин соединены последовательно. Тогда жесткость всего соединения равна:
[frac{1}{k}=frac{1}{k_1}+frac{1}{k_2}+dots =sumlimits^N_{ i=1}{frac{1}{k_i}left(3right),}]
где $k_i$ — жесткость $i-ой$ пружины.
При последовательном соединении пружин жесткость системы определяют как:
[k=k_1+k_2+dots +sumlimits^N_{i=1}{k_i}left(4right).]
Примеры задач с решением
Пример 1
Задание. Пружина в отсутствии нагрузки имеет длину $l=0,01$ м и жесткость равную 10 $frac{Н}{м}. $Чему будет равна жесткость пружины и ее длина, если на пружину действовать силой $F$= 2 Н? Считайте деформацию пружины малой и упругой.
Решение. Жесткость пружины при упругих деформациях является постоянной величиной, значит, в нашей задаче:
[k=k’left(1.1right).]
При упругих деформациях выполняется закон Гука:
[F=kDelta l left(1.2right).]
Из (1.2) найдем удлинение пружины:
[Delta l=frac{F}{k}left(1.3right).]
Длина растянутой пружины равна:
[l’=l+Delta l=l+frac{F}{k}.]
Вычислим новую длину пружины:
[l’=0,01+frac{2}{10}=0,21 left(мright).]
Ответ. 1) $k’=10 frac{Н}{м}$; 2) $l’=0,21$ м
Пример 2
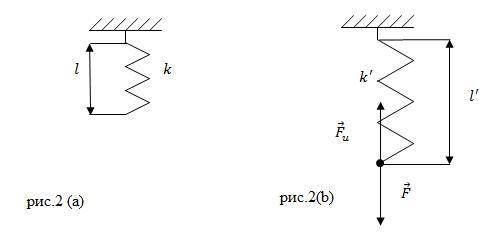
Задание. Две пружины, имеющие жесткости $k_1$ и $k_2$ соединили последовательно. Какой будет удлинение первой пружины (рис.3), если длина второй пружины увеличилась на величину $Delta l_2$?
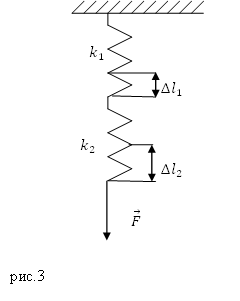
Решение. Если пружины соединены последовательно, то деформирующая сила ($overline{F}$), действующая на каждую из пружин одинакова, то есть можно записать для первой пружины:
[F=k_1Delta l_1left(2.1right).]
Для второй пружины запишем:
[F=k_2Delta l_2left(2.2right).]
Если равны левые части выражений (2.1) и (2.2), то можно приравнять и правые части:
[k_1Delta l_1=k_2Delta l_2left(2.3right).]
Из равенства (2.3) получим удлинение первой пружины:
[Delta l_1=frac{k_2Delta l_2}{k_1}.]
Ответ. $Delta l_1=frac{k_2Delta l_2}{k_1}$
Читать дальше: формула закона Архимеда.
Источник
/
/
Растяжение пружины формула физика
Сила упругости возникает в результате электромагнитного взаимодействия между молекулами и атомами вещества.
Самый простой вариант деформации можно рассмотреть на примере сжатия и растяжения пружины.
На данном рисунке (x > 0) — деформация растяжения; (x — деформация сжатия. (Fx) — внешняя сила.
В том случае, когда деформация самая незначительная, т.е малая, сила упругости направлена в сторону, которая является противоположной по направлению перемещающихся частиц тела и пропорциональна деформации тела:
Fx = Fупр = – kx
С помощью данного соотношения выражен закон Гука, который был установлен экспериментальным методом. Коэффициент k принято называть жесткостью тела. Жесткость тела измеряется в ньютонах на метр (Н/м) и зависит от размеров и формы тела, а также от того, из каких материалов состоит данное тело.
Закон Гука в физике для определения деформации сжатия или растяжения тела записывают совершенно в другой форме. В данном случае относительной деформацией называется
Роберт Гук
Английский естествоиспытатель, учёный-энциклопедист
отношение ε = x / l . В то же время напряжением называется площадь поперечного сечения тела после относительной деформации:
σ = F / S = –Fупр / S
В данном случае закон Гука формулируют так: напряжению σ пропорциональна относительная деформация ε . В данной формуле коэффициент Е называют модулем Юнга. Данный модуль не зависит от формы тела и его размеров, но в то же время, напрямую зависит от свойств материалов, из которого состоит данное тело. Для различных материалов модуль Юнга колеблется в достаточно широком диапазоне. Например, для резины E ≈ 2·106 Н/м2, а для стали E ≈ 2·1011 Н/м2 (т.е. на пять порядков больше).
Вполне допустимо обобщить закон Гука и в тех случаях, когда совершаются более сложные деформации. Например, рассмотрим деформацию изгиба. Рассмотрим стержень, который лежит на двух опорах и имеет существенный прогиб.
Со стороны опоры (или подвеса) на данное тело действует упругая сила, это сила реакции опоры. Сила реакции опоры при соприкосновении тел будет направлена к поверхности соприкосновения строго перпендикулярно. Такую силу принято называть силой нормального давления.
Рассмотрим второй вариант. Путь тело лежит на неподвижном горизонтальном столе. Тогда реакции опоры уравновешивает силу тяжести и направлена она вертикально вверх. Причем весом тела считают силу, с которой тело воздействует на стол.
Каждый из нас знает, что такое пружина . И мы знаем, что пружину можно удлинять или же, наоборот, укорачивать, если приложить к ней силу.
Поскольку для того, чтобы удлинить или укоротить пружину, требуется усилие, логично предположить, что пружина оказывает «сопротивление» при ее деформации (растяжении или же сжатии) — в ней возникает сила. Это сила упругости F у п р у г о с т и F_ <упругости>F у п р у г о с т и .
Можно заметить, что чем больше мы пытаемся удлинить пружину (или чем больше укоротить ее), тем бОльшую силу приходится прикладывать к пружине. Тем большая сила упругости возникает в пружине.
Но пружины бывают разные. Некоторые легко поддаются деформации усилием человека. Некоторые — сложно. Так, например, не составляет труда сжать пружину детского пистолета на несколько сантиметров. Пружину же в амортизаторе машины сжать на те же несколько сантиметров намного сложнее. Должна существовать какая-то величина, которая отражала бы то, что пружины бывают разные. И такая величина есть: это k k k — коэффициент упругости (коэффициент жесткости, жесткость). Чем сложнее сжать пружину, тем больше k k k . То есть более жесткая пружина имеет бОльшую по величине жесткость k k k . Чем больше k k k — тем больше сила упругости, которая возникает в пружине.
Наши рассуждения о влиянии удлинения (укорочения) и жесткости пружины на силу упругости закреплены в законе Гука:
Однако закон Гука выполняется не всегда. Закон Гука справедлив только для пластичных деформаций. Это такие деформации, при которых тело полностью восстанавливает свою форму и размеры после исчезновения сил, деформирующих тело. Короче говоря, закон Гука будет выполняться и деформации будут пластичными в том случае, когда растянутая или сжатая пружинка вернет себе форму после того, как ее перестанут растягивать или сжимать. Если пружину растянуть слишком сильно, то она может так и остаться растянутой. Деформации, которым она подверглась, были непластичными, и закон Гука выполнялся не везде.
Задачи для самостоятельного решения: #сила упругости
В общем сделал лабу и там есть формула
1/k=1/k1+1/k2
k – коэффициент жёсткости
две пружины соединены последовательно. надо найти их совместный коэффициент жёсткости.
и препод подчеркнула эту строчку и подписала: вывод формулы.
что ей написать? какой вывод? из чего можно её вывести?
Источник
Сил упругости возникает при деформации физического тела, то есть когда изменяются размеры и форма тела. Эта сила направлена в сторону, противоположную силе, создающей деформацию. На примере пружины выясним как сила упругости связана с величиной деформации. Рассмотрим также причины возникновения упругих сил.

Закон Гука
Пружину можно сжимать, растягивать, изгибать или скручивать. В каждом из этих случаев будут возникать силы упругости, стремящиеся вернуть форму и размеры пружины в начальное состояние. Для понимания основных закономерностей будем рассматривать только линейные сжатия и растяжения (вдоль оси х). Для вычисления сил при деформациях изгибов и скручивании требуется применение более сложного математического аппарата.

Рис. 1. Деформации растяжения и сжатия пружины.
Если начальная длина, ненапряженной пружины, равна L0, то для малых деформаций выполняется закон Гука, открытый экспериментально:
$ F_уп = − k * Δх $ (1),
где, в формуле силы упругости пружины:
Fуп — сила упругости пружины, Н;
k — коэффициент жесткости пружины, Н/м;
Δх —величина деформации (дельта икс), м.
Величина малых деформаций должна быть намного меньше начальной длины пружины:
$ Δх
Рис. 2. Портрет Роберта Гука.
Этот фундаментальный закон был открыт английским ученым Робертом Гуком в 1660г. Кроме этого он сделал много других замечательных изобретений и экспериментов:
- открыл эффект образования цветов тонких пленок, которое в оптике называется явлением интерференции;
- предложил модель волнообразного распространения света;
- сформулировал предположение о связи теплоты с движением частиц, из которых состоит тело;
- изобрел спиральную пружину для регулировки часов, усовершенствовал барометр, гигрометр, анемометр.
Источник силы упругости
Происхождение сил упругости связано с электромагнитным взаимодействием молекул и атомов. Когда происходит увеличение размеров пружины (растяжении), то силы взаимного притяжения “пытаются” восстановить начальные размеры. При сжатии пружины начинают работать силы отталкивания. Когда тело не деформировано, расстояние между молекулами соответствует равенству сил притяжения и отталкивания.
Динамометры
Упругие свойства пружин используются в приборах для измерения силы. Обычно динамометр состоит из двух основных частей: пружины (упругий элемент) и шкалы устройства, на которой нанесены цифровые значения силы или массы, если этот прибор предназначен для бытового применения. Измеряемое усилие прикладывается к пружине, которая деформируется и сдвигает стрелку прибора вдоль отсчетной шкалы.

Рис. 3. Пружинные динамометры.
Хотя закон Гука и считается универсальным, но диапазон деформаций в котором он выполняется сильно отличается для разных тел. Например, в металлических проволоках (прямолинейных) и стержнях максимальная величина относительной деформации (отношение Δх к L0), для которой еще будет справедлив закон Гука, составляет не более 1%. При больших деформациях наступают необратимые разрушения материалов.
Что мы узнали?
Итак, мы узнали, что сила упругости пружины прямо пропорциональна величине деформации тела и направлена в сторону, обратную направлению сдвига пружины. Силы упругости связаны с электромагнитным взаимодействием молекул и атомов. При сжатии включается механизм отталкивания электрических одноименных зарядов. При растяжении — начинает работать механизм притяжения разноименных зарядов.
Тест по теме
Оценка доклада
Средняя оценка: 4.7. Всего получено оценок: 76.
Источник
Сила упругости
Любое тело, когда его деформируют и оказывают внешнее воздействие, сопротивляется и стремиться восстановить прежние форму и размеры. Это происходит по причине электромагнитного взаимодействия в теле на молекулярном уровне.
Деформация — изменение положения частиц тела друг относительно друга. Результат деформации — изменение межатомных расстояний и перегруппировка блоков атомов.
Определение. Что такое сила упругости?
Сила упругости — сила, возникающая при деформации в теле и стремящаяся вернуть тело в начальное состояние.
Рассмотрим простейшие деформации — растяжение и сжатие
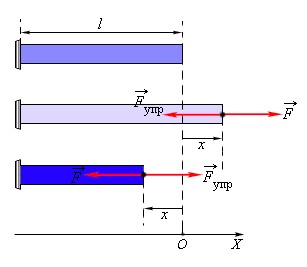
На рисунке показано, как действует сила упругости, когда мы сжимаем или растягиваем стержень.
Закон Гука
Для малых деформаций x≪ l справедлив закон Гука.
Закон Гука
Деформация, возникающая в упругом теле, пропорциональна приложенной к телу силе.
Fупр=-kx
Здесь k — коэффициент пропорциональности, называемый жесткостью. Единица измерения жесткости системе СИ Ньютон на метр. Жесткость зависит от материала тела, его формы и размеров.
Знак минус показывает, что сила упругости противодействует внешней силе и стремится вернуть тело в первоначальное состояние.
Существуют и другие формы записи закона Гука. Относительной деформацией тела называется отношение ε=xl. Напряжением в теле называется отношение σ=-FупрS. Здесь S — площадь поперечного сечения деформированного тела. Вторая формулировка закона Гука: относительная деформация пропорциональна напряжению.
ε=σE.
Здесь E — так называемый модуль Юнга, который не зависит от формы и размеров тела, а зависит только от свойств материала. Значение модуля Юнга для различных материалов широко варьируется. Например, для стали E≈2·1011 Нм2, а для резины E≈2·106 Нм2
Закон Гука можно обобщить для случая сложных деформаций. Рассмотрим деформацию изгиба стержня. При такой деформации изгиба сила упругости пропорциональна прогибу стержня.

Концы стержня лежат на двух опорах, которые действуют на тело с силой N→, называемой силой нормальной реакции опоры. Почему нормальной? Потому что эта сила направлена перпендикулярно (нормально) поверхности соприкосновения.
Если стержень лежит на столе, сила нормальной реакции опоры направлена вертикально вверх, противоположно силе тяжести, которую она уравновешивает.
Вес тела — это сила, с которой оно действует на опору.
Силу упругости часто рассматривают в контексте растяжения или сжатия пружины. Это распространенный пример, который часто встречается не только в теории, но и на практике. Пружины используются для измерения величины сил. Прибор, предназначенный для этого — динамаметр.
Динамометр — пружина, растяжение которой проградуированно в единицах силы. Характерное свойство пружин заключается в том, что закон Гука для них применим при достаточно большом изменении длины.
При сжатии и растяжении пружины действует закон Гука, возникают упругие силы, пропорциональные изменению длины пружины и ее жесткости (коэффициента k).
В отличие от пружин стержни и проволоки подчиняются закону Гука в очень узких пределах. Так, при относительной дефомации больше 1% в материале возникают необратимые именения — текучесть и разрушения.
Источник
