Растяжение под действием собственного веса
Растяжение под действием собственного веса
[c.200]
Пример 12.1. Определить абсолютное удлинение, возникающее под действием собственного веса, свободно висящей проволоки длиной I из отожженной меди, диаграмма растяжения которой представлена на рис. 411. Зависимость удлинения е от напряжения а может быть представлена степенной функцией
[c.357]
Удлинение бруса постоянного сечения под действием собственного веса в 2 раза меньше удлинения при растяжении силой, равной собственному весу и приложенной к концу бруса.
[c.201]
Построить эпюру относительных деформаций стержня рис. а), находящегося под действием собственного веса (удельный вес материала у). Материал стержня обладает линейным упрочнением, диаграмма растяжения которого изображена на рис. б. Найти
[c.30]
Растяжение призматического бруса под действием собственного веса.
[c.92]
Растяжение призматического бруса под действием собственного веса. Вертикально расположенный призматический брус (рис. 4.3) длиной I закреплен по верхнему торцу и находится под действием собственного веса. Начало координат О совместим с центром тяжести нижнего торца недеформированного бруса, направив ось Хз вверх по оси бруса.
[c.85]
Если для данного материала известно максимальное напряжение, которое он может выдержать при растяжении, то по формуле (3.31) можно оценить наибольшую длину троса или стержня из этого материала, при котором он не разорвется под действием собственного веса. Такие оценки необходимы, например, при расчете труб, которые опускаются в нефтяные скважины (в настоящее время имеются скважины глубиной 5—6 км и больше).
[c.332]
Для испытаний на растяжение со скоростью до 25 м/с на вертикальном копре используется эффект изменения интенсивности упругой волны при ее распространении по стержню со ступенчатым изменением сечения [262]. Схема такого копра представлена на рис. 34. Образец 4 посредством резьбовых головок соединяется с динамометром 2 и ступенчатым стержнем-волноводом 6, который оканчивается легкой наковальней 9, воспринимающей удар падающей под действием собственного веса бабы 8. Баба поднимается на требуемую высоту подъемным механизмом (на рисунке не показан) с помощью тросов 7.
[c.97]
ПРОЧНОСТЬ УДЕЛЬНАЯ — обычно отношение предела прочности материала при растяжении в кг/см к его удельному весу у в г/сл1 . Имеет размерность длины см) и физически характеризует длину стержня сечением 1 см , при к-рой последний разрушается под действием собственного веса. П. у. является основным критерием при выборе материалов для деталей, у к-рых расчетной является разрушающая нагрузка при растяжении. При этом для всех сравниваемых материалов
[c.92]
Перемещения точек стержня при кручении могут быть найдены таким же способом, как и в только что рассмотренном случае растяжения стержня под действием собственного веса.. Перемещения эти представятся формулами
[c.67]
Винт рассчитывают на сложное напряженное состояние от изгиба под действием собственного веса, растяжения или сжатия под действием продольной силы Р и кручения под действием крутящего момента.
[c.273]
Прочность растущей упругой сосульки. Один из основных вопросов, возникающих в связи с рассмотрением задачи наращивания сосульки, заключается в предсказании момента ее разрушения и отрыва под действием собственного веса. В качестве условия прочности и хрупкого разрушения льда в состоянии упругого деформирования обычно используется критерий максимальных допустимых напряжений [1, 2]. Величину допустимого напряжения при упругом растяжении ледяного образца обозначим через а. Тогда условие локального хрупкого разрушения сосульки, занимающей в момент разрушения область 2, имеет вид
[c.9]
Всестороннее сжатие (244). Растяжение цилиндрического стержня (245). Деформация цилиндрического стержня под действием собственного веса (246). Чистый изгиб стержня (248). Кручение призматических стержней (250). Циркуляция касательных напряжений (258). Различные формы постановки задачи о кручении (259). Мембранная аналогия Прандтля (266).
[c.8]
Растяжение призматического стержня под действием собственного веса. Если — вес единицы объема стержня (фиг. 120), то объемные силы равняются
[c.244]
РАСТЯЖЕНИЕ ПРИЗМЫ ПОД ДЕЙСТВИЕМ СОБСТВЕННОГО ВЕСА Интегрируя уравнения (5.34), получаем
[c.123]
Растяжение призмы под действием собственного веса 122 Расширение объемное 287 Релея волна 292
[c.363]
Растяжение стержней распределенными силами. Стержень под действием собственного веса и растягивающего усилия (рис. 3). Напряжение растяжения в сечении г
[c.184]
Поведение металла, подвергающегося длительной механической нагрузке в вакуумном приборе при повышенной температуре, нельзя предсказать, зная лишь его временное сопротивление разрыву, измеренное при обычных испытаниях на разрыв, причем это тем труднее, чем ближе рабочая температура. металла к его температуре рекристаллизации. При определенном напряжении растяжения, которое лежит значительно ниже предела текучести холодного металла, материал начинает непрерывно течь (рис. 2-6, кривые 5 и 6), а его сечение — непрерывно уменьшаться (например, у натянутых катодов), что в конце концов приводит к его разрушению. В других случаях процесс текучести хотя и не приводит к разрушению металла, но вызывает нежелательное изменение формы деталей (провисание проволоки сеток, катодных спиралей и других деталей под действием собственного веса) часто даже тогда, когда термическая нагрузка кратковременна (например, при обезгаживании).
[c.11]
Ог — напряжение от растяжения под действием внутреннего давления в продольной плоскости, проходящей через ось трубы с, — напряжение от изгиба под действием собственного веса трубопровода, а также веса тепловой изоляции и теп-
[c.97]
| Рис. 1.2. Эпюры продольной силы, напряжений и перемещений в задаче о растяжении стержня под действием собственного веса. | 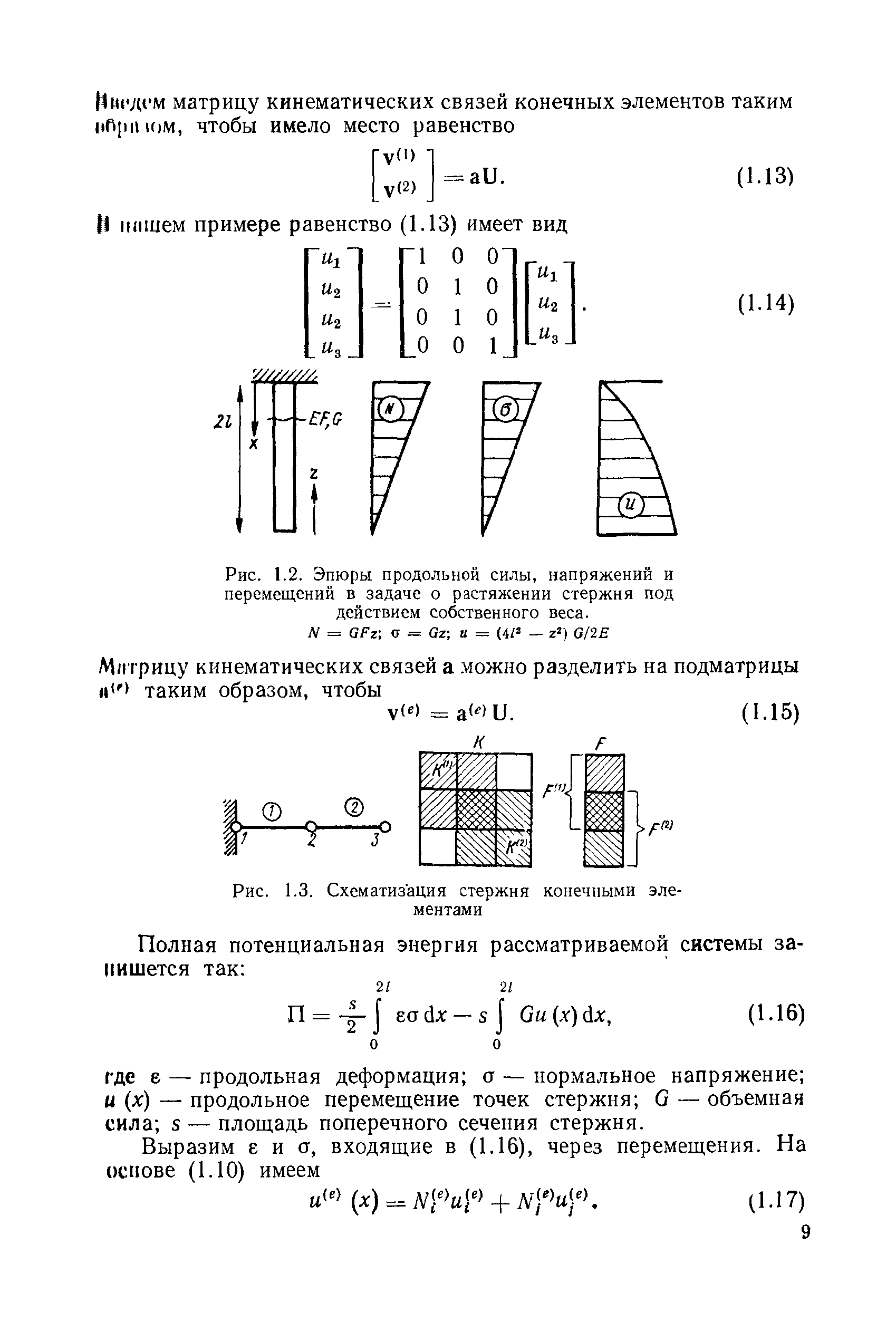 |
В предыдущих главах подробно изложена процедура МКЭ па примере симплекс-элементов, т. е. конечных элементов с линейной или простейшей из возможных аппроксимаций для искомых функций. Однако уже анализ решения задачи о растяжении стержня под действием собственного веса (см. рис. 1.5) показывает, что использование симплекс-элементов в этом случае не дает удовлетворительных результатов. При этом возникает естественное желание увеличить порядок интерполяционного полинома для перемещений. Например, от линейной аппроксимации перемещений в элементе перейти к квадратичной, чтобы при дифференцировании перемещений получить линейно изменяющиеся в элементе напряжения.
[c.69]
Задача 1.1.9. Найти з изменения площадей поперечного сечения бруса равного сопротивления, испытывающего растяжение под действием силы и собственного веса.
[c.25]
Данное нами определение фермы является идеализированным. Однако оно позволяет произвести расчет реальных ферм, которые встречаются на практике, наиболее простым способом и получить результаты, достаточно близкие к действительности. В реальной ферме стержни, конечно, обладают весом и соединяются между собой не шарнирно, а наглухо, при помош,и сварки или заклепок. Вследствие этого стержни реальной фермы будут еще и изгибаться под действием собственного веса. Но так как вес каждого стержня реальной фермы обычно является незначительным по сравнению с силами, приложенными в ее узлах , то для простоты расчета иммож-но пренебречь. Считая при этом ферму состоящей из прямолинейных стержней, соединенных между собой при помощи идеальных (лишенных трения) шарниров, мы приходим к заключению, что каждый стержень будет испытывать сжатие или растяжение и не будет подвергаться изгибу.
[c.141]
Рассмотрим теперь задачу о растяжении цилиндрического бруса под действием собственного веса. При этом сохраним неизменными основные предположения, при которых решалась первая задача о растяжении бруса под действием поверхностных сил, распределенных по его торцам, а именно предположим, что Т = То = = onst, e j-= о, но F = gi и = 0 всюду на внешней поверхности бруса, за исключением торца А, где брус закреплен.
[c.328]
Предел прочности при растяжении текстильных волокон колеблется в широких пределах от 16— 18 кг1мм для шерсти до 220 кг1мм для стекловолокна и 300 кг мм для асбеста. Ввиду затруднительности точного измерения размеров поперечного сечения пряжи, тканей и др. изделий принято пользоваться для сравнения текстильных материалов разных размеров понятием разрывной длины, определяемой как отношение предела прочности материала к весу единицы его длины. Разрывной длиной является та минимальная длина материала, при которой он, будучи свободно подвешен, разорвется под действием собственного веса. Разрывная длина характеризует удельную весовую прочность, особенно важную для материалов авиационного назначения. Поэтому в табл. 25 и далее при описании отдельных текстильных материалов приводятся значения их разрывных длин.
[c.295]
Рассчитываются эти связи только на растяжение, хотя в действительности работают частично и на изгиб под действием собственного веса (тряска паровоза). Допускаемое напряжение в этих связях—/ ,е 900 кг1см .
[c.99]
Рассмотрим теперь другой крайний случай, в котором А равняется йулЬ, т. е. тело внезапно положено на опору тл (рис. 264) без начальной скорости. Хотя в этом случае мы не имеем кинетической энергий в начале растяжения стержня все таки эта задача совершенно отлична ог задачи при статическом нагружении стержня. В случае статического растяжения мы предполагаем постепенное приложение нагрузки и, Следовательно, вСегда существующее равновесие между действующей нагрузкой и сопротивляющимися силами упругости в стержне. При этих условиях вопрос о кинетической энергии не входит в задачу. В случае внезапного приложения нагрузки удлинение стержня и напряжение в стержне в начале равны нулю, и внезапно приложенный груз начинает падать под действием собственного веса. 1Во время этого движения сила сопротивления стержня постепенно увеличивается, и, когда она
[c.259]
Пример. Найти закон изменения площади поперечного сечений бруса равйого сопротивления, испытывающего растяжение под действием силы Р и собственного веса (рис. 2.14, а). Решение. В каждом сечении бруса равного сопротивления
[c.29]
Для пояснения он указывает Небольшие обелиск, колонна или иная строительная деталь могут быть установлены без всякой опасности обрушения, между тем как весьма крупные элементы этого типа распадаются на части из-за малейших причин, а то и просто под действием своего собственного веса . Чтобы подтвердить это, он начинает с исследования прочности материалов при простом растяжении (рис. 12) и устанавливает, что прочность бруса пропорциональна плопцади его поперечного сечения и не зависит от его длины. Такую прочность бруса Галилей называет абсолютным сопротивлением разрыву и приводит несколько числовых значений, характеризующих прочность меди. Определив абсолютное сопротивление бруса, Галилей исследует сопротивление разрушению того же бруса в том случае, когда он используется как консоль и нагружен на свободном конце (рис. 13). Он утверждает Ясно, что если призматический брус подвергнется излому, этот излом произойдет в точке В, причем ребро гнезда играет роль оси вращения для рычага ВС, к которому приложена сила толщина В А бруса представляет собой другое плечо, вдоль которого распределяется сопротивление. Это сопротивление препятствует отделению части BD, лежащей вне стены, от части, лежащей внутри ее. Из сказанного следует, что величина силы, приложенной в С, относится к величине сопротивления, обусловленного толщиной призмы, т. е. сцеплением основания В А с примыкающими к нему частями бруса, точно так же, как половина длины ВА относится к длине ВС ). Мы видим, что
[c.21]
Источник
Сопротивление материалов
Решение задач на растяжение и сжатие
Расчеты на прочность при растяжении и сжатии
В результате проведения механических испытаний устанавливают предельные напряжения, при которых происходит нарушение работы или разрушение деталей конструкции.
Предельным напряжением при статической нагрузке для пластичных материалов является предел текучести, для хрупких — предел прочности.
Для обеспечения прочности деталей необходимо, чтобы возникающие в них в процессе эксплуатации наибольшие напряжения были меньше предельных.
Отношение предельного напряжения к напряжению, возникающему в процессе работы детали, называют коэффициентом запаса прочности и обозначают буквой s:
s = σпред / σ,
где σ = N / А – реальное напряжение, возникающее в элементе конструкции.
Недостаточный коэффициент запаса прочности может привести к потере работоспособности конструкции, а избыточный (слишком высокий) — к перерасходу материала и утяжелению конструкции. Минимально необходимый коэффициент запаса прочности называют допускаемым, и обозначают [s].
Отношение предельного напряжения к допускаемому запасу прочности называют допускаемым напряжением, и обозначают [σ]:
[σ] = σпред / [s].
Условие прочности в деталях и конструкциях заключается в том, что наибольшее возникающее в ней напряжение (рабочее напряжение) не должно превышать допускаемого:
σmax≤ [σ], или в другом виде: s ≥ [s].
Если допускаемые напряжения при растяжении и сжатии различны, их обозначают [σр] и [σс].
Расчетная формула при растяжении и сжатии имеет вид:
σ = N / А ≤ [σ]
и читается следующим образом: нормальное напряжение в опасном сечении, вычисленное по формуле σ = N /А, не должно превышать допустимое.
На практике расчеты на прочность проводят для решения задач:
— проектный расчет, при котором определяются минимальные размеры опасного сечения;
— проверочный расчет, при котором определяется рабочее напряжение и сравнивается с предельно допустимым;
-определение допускаемой нагрузки при заданных размерах опасного сечения.
***
Растяжение под действием собственного веса
Если ось бруса вертикальна, то его собственный вес вызывает деформацию растяжения или сжатия. 
Рассмотрим брус постоянного сечения весом G, длиной l, закрепленный верхним концом и нагруженный только собственным весом G (рис.1).
Для определения напряжений в поперечном сечении на переменном расстоянии z от нижнего конца применим метод сечений.
Рассмотрим равновесие нижней части бруса и составим уравнение равновесия:
Σ Z = 0; Nz — Gz = 0, откуда:
Nz = Gz = γ А z,
где γ — удельный вес материала бруса, А – площадь его поперечного сечения, z — длина части бруса от свободного конца до рассматриваемого сечения.
Напряжения, возникающие в сечениях бруса, нагруженного собственным весом, определяются по формуле:
σz = Nz / А = γ А z / А = γ z,
т. е. для нагруженного собственным весом бруса нормальное напряжение не зависит от площади поперечного сечения. Очевидно, что опасное сечение будет находиться в заделке:
σmax = γ l.
Эпюра распределения напряжений вдоль оси бруса представляет собой треугольник.
Если требуется определить максимальную длину бруса, нагруженного собственным весом, используют расчет по предельному допустимому напряжению в сечении:
lпр = [σ] / γ.
***
Статически неопределимые задачи
Иногда в практике расчета конструкций требуется определить неизвестные силовые факторы (например, реакции связей или внутренние силы), при этом количество неизвестных силовых факторов превышает количество возможных уравнений равновесия для данной конструкции, и расчет произвести рассмотренными ранее способами не представляется возможным.
Задачи на расчет конструкций, в которых внутренние силовые факторы не могут быть определены с помощью одних лишь уравнений равновесия статики, называют статически неопределимыми. Подобные задачи нередко встречаются при расчете конструкций, подверженных температурным деформациям.
Для решения таких задач помимо уравнений равновесия составляют уравнение перемещений или деформаций.
Рассмотрим невесомый стержень постоянного сечения площадью А, длиной l, жестко защемленный по концам (см. рис. 2). 
При нагревании в стержне возникают температурные напряжения сжатия.
Попробуем определить эти напряжения.
Составим для стержня уравнение равновесия:
Σ Z = 0; RС — RВ = 0,
откуда следует, что реакции RС и RВ равны между собой, а применив метод сечений установим, что продольная сила N в сечениях стержня равна неизвестным реакциям:
N = RС = RВ.
Составим дополнительное уравнение, для чего мысленно отбросим правую заделку и заменим ее реакцией RВ, тогда дополнительное уравнение деформации будет иметь вид:
Δlt = ΔlСВ
т. е. температурное удлинение стержня равно его укорочению под действием реакции RB, так как связи предполагаются абсолютно жесткими.
Температурное удлинение стержня определяется по формуле: Δlt = αtl, где α — коэффициент линейного расширения стержня.
Укорочение стержня под действием реакции: ΔlСВ = RB l / (EА).
Приравняв правые части равенств, получим:
αtl = RB l / (EА), откуда RB = αtEА.
Температурные напряжения в реальных конструкциях могут достигать значительных величин. Чтобы исключить их отрицательное влияние на прочность конструкций, прибегают к различным методам. Мосты, например, закрепляют лишь на одном конце (на одном берегу), а второй конец оставляют подвижным.
В длинных трубопроводах, подверженных температурным напряжениям, делают компенсирующие карманы, петли и т. д.
***
Материалы раздела «Растяжение и сжатие»:
- Примеры решения задач по сопромату.
- Основные понятия о деформации растяжения и сжатия.
- Деформации при растяжении и сжатии. Потенциальная энергия деформации растяжения.
Срез
Правильные ответы на вопросы Теста № 6
№ вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Правильный вариант ответа | 2 | 1 | 1 | 3 | 3 | 2 | 1 | 3 | 2 | 1 |
Источник
Подбор сечений с учетом собственного веса (при растяжении и сжатии).
При установлении внешних сил, растягивающих или сжимающих элементы конструкций, мы до сих пор игнорировали собственный вес этих элементов. Возникает вопрос, не вносится ли этим упрощением расчета слишком большая погрешность? В связи с этим подсчитаем величины напряжений и деформаций при учете влияния собственного веса растянутых или сжатых стержней.
Пусть вертикальный стержень (Рис.1, а) закреплен своим верхним концом; к нижнему его концу подвешен груз Р. Длина стержня l, площадь поперечного сечения F, удельный вес материала и модуль упругости Е. Подсчитаем напряжения по сечению АВ, расположенному на расстоянии от свободного конца стержня.
а) б)
Рис.1. Исходная расчетная схема бруса а) и б) равновесие нижней отсеченной части.
Рассечем стержень сечением АВ и выделим нижнюю часть длиной с приложенными к ней внешними силами (Рис.1, б) грузом Р и ее собственным весом . Эти две силы уравновешиваются напряжениями, действующими на площадь АВ от отброшенной части. Эти напряжения будут нормальными, равномерно распределенными по сечению и направленными наружу от рассматриваемой части стержня, т. е. растягивающими. Величина их будет равна:
Таким образом, при учете собственного веса нормальные напряжения оказываются неодинаковыми во всех сечениях. Наиболее напряженным, опасным, будет верхнее сечение, для которого достигает наибольшего значения l; напряжение в нем равно:
Условие прочности должно быть выполнено именно для этого сечения:
Отсюда необходимая площадь стержня равна:
От формулы, определяющей площадь растянутого стержня без учета влияния собственного веса, эта формула отличается лишь тем, что из допускаемого напряжения вычитается величина .
Чтобы оценить значение этой поправки, подсчитаем ее для двух случаев. Возьмем стержень из мягкой стали длиной 10 м; для него , а величина . Таким образом, для стержня из мягкой стали поправка составит т. е. около 0,6%. Теперь возьмем кирпичный столб высотой тоже 10 м; для него , а величина Таким образом, для кирпичного столба поправка составит , т.е. уже 15%.
Вполне понятно, что влиянием собственного веса при растяжении и сжатии стержней можно пренебрегать, если мы не имеем дела с длинными стержнями или со стержнями из материала, обладающего сравнительно небольшой прочностью (камень, кирпич) при достаточном весе. При расчете длинных канатов подъемников, различного рода длинных штанг и высоких каменных сооружений (башни маяков, опоры мостовых ферм) приходится вводить в расчет и собственный вес конструкции.
В таких случаях возникает вопрос о целесообразной форме стержня. Если мы подберем сечение стержня так, что дадим одну и ту же площадь поперечного сечения по всей длине, то материал стержня будет плохо использован; нормальное напряжение в нем дойдет до допускаемого лишь в одном верхнем сечении; во всех прочих сечениях мы будем иметь запас в напряжениях, т. е. излишний материал. Поэтому желательно так запроектировать размеры стержня, чтобы во всех его поперечных сечениях (перпендикулярных к оси) нормальные напряжения были постоянны,
Такой стержень называется стержнем равного сопротивления растяжению или сжатию. Если при этом напряжения равны допускаемым, то такой стержень будет иметь наименьший вес.
Возьмем длинный стержень, подверженный сжатию силой Р и собственным весом (Рис.2). Чем ближе к основанию стержня мы будем брать сечение, тем больше будет сила, вызывающая напряжения в этом сечении, тем большими придется брать размеры площади сечения. Стержень получит форму, расширяющуюся книзу. Площадь сечения F будет изменяться по высоте в зависимости от , т. е. .
Установим этот закон изменения площади в зависимости от расстояния сечения от верха стержня.
Рис.2. Расчетная схема бруса равного сопротивления
Площадь верхнего сечения стержня определится из условия прочности:
и
где допускаемое напряжение на сжатие; напряжения во всех прочих сечениях стержня также должны равняться величине
Чтобы выяснить закон изменения площадей по высоте стержня, возьмем два смежных бесконечно близких сечения на расстоянии от верха стержня; расстояние между сечениями ; площадь верхнего назовем , площадь же смежного .
Приращение площади при переходе от одного сечения к другому должно воспринять вес элемента стержня между сечениями. Так как на площади он должен вызвать напряжение, равное допускаемому , то определится из условия:
Отсюда:
После интегрирования получаем:
При площадь ; подставляя эти значения, имеем:
и
Отсюда
,
Если менять сечения точно по этому закону, то боковые грани стержня получат криволинейное очертание (Рис.2), что усложняет и удорожает работу. Поэтому обычно такому сооружению придают лишь приближенную форму стержня равного сопротивления, например в виде усеченной пирамиды с плоскими гранями. Приведенный расчет является приближенным. Мы предполагали, что по всему сечению стержня равного сопротивления передаются только нормальные напряжения; на самом деле у краев сечения напряжения будут направлены по касательной к боковой поверхности.
В случае длинных канатов или растянутых штанг форму стержня равного сопротивления осуществляют тоже приближенно, разделяя стержень по длине на ряд участков; на протяжении каждого участка сечение остается постоянным (Рис.3) получается так называемый ступенчатый стержень.
Рис.3. Эквивалентный ступенчатый брус с приближением к модели бруса равного сопротивления
Определение площадей … при выбранных длинах производится следующим образом. Площадь поперечного сечения первого нижнего участка будет по формуле равна:
Чтобы получить площадь поперечного сечения второго участка, надо нагрузить его внешней силой Р и весом первого участка:
Для третьего участка к внешней силе добавляются веса первого и второго участков. Подобным же образом поступают и для других участков.
Деформации при действии собственного веса.
При определении влияния собственного веса на деформацию при растяжении и сжатии стержней придется учесть, что относительное удлинение различных участков стержня будет переменным, как и напряжение . Для вычисления полного удлинения стержня постоянного сечения определим сначала удлинение бесконечно малого участка стержня длиной , находящегося на расстоянии от конца стержня (Рис.4).
Рис.4. Расчетная модель бруса с учетом собственного веса.
Абсолютное удлинение этого участка равно
Полное удлинение стержня равно:
Величина представляет собой полный вес стержня. Таким образом, для вычисления удлинения от действия груза и собственного веса можно воспользоваться прежней формулой:
подразумевая под S внешнюю силу и половину собственного веса стержня.
Что же касается деформаций стержней равного сопротивления, то, так как нормальные напряжения во всех сечениях одинаковы и равны допускаемым , относительное удлинение по всей длине стержня одинаково и равно
Абсолютное же удлинение при длине стержня l равно:
где обозначения соответствуют приведенным на рис.1.
Деформацию ступенчатых стержней следует определять по частям, выполняя подсчеты по отдельным призматическим участкам. При определении деформации каждого участка учитывается не только его собственный вес, но и вес тех участков, которые влияют на его деформацию, добавляясь к внешней силе. Полная деформация получится суммированием деформаций отдельных участков.
Дальше…
Источник
