Растяжение и сжатие расчет и построение эпюры
Первая тема сопротивления материалов — это растяжение-сжатие. Задачи на растяжение сжатие в сопромате — довольно простая тема. И сейчас я это докажу.
Прежде всего растяжение — мы интуитивно понимаем — удлинение, увеличение размеров. А сжатие — уменьшение длины, укорочение.
При изучении растяжения-сжатия используется один и тот же подход ко всем задачам, ко всем расчетным схемам. А именно — метод сечений. О нем мы расскажем в отдельной записи. А пока, ниже вы видите видео уроки на эту тему. Надеюсь вам будет полезно и удобно изучать эту тему со мной.
Что такое растяжение-сжатие
Прежде всего нужно сказать, что растяжение-сжатие — это такой вид деформации (относительного изменения размеров), при котором одно плоское сечение относительно другого удаляется параллельно исходному положению.
 Пример деформации растяжения-сжатия. Схема приложения
Пример деформации растяжения-сжатия. Схема приложенияВсе это звучит сложно, но посмотрите видео и Вы все поймете!
Подход в решении задач на растяжение-сжатие
Видео урок — Как отличить растяжение от сжатия. Приводится объяснение основного метода расчета задач по сопротивлению материалов — метод сечений
В первом видео уроке объясняется сам процес возникновения деформации растяжения-сжатия. Как отличить растяжение от сжатия. Приводится объяснение основного метода расчета задач по сопротивлению материалов — метод сечений.
Здесь рассмотрены задачи для стержня, имеющего сплошное поперечное сечение. На такой стержень может действовать как одна сила, так и несколько.
Растяжение-сжатие в стержневых конструкциях
видео урок Растяжение-сжатие в стержневых конструкциях
Во втором видео уроке приводится решение задачи на растяжение-сжатие для системы стержневых конструкций. Приведены методика и план решения задачи по сопротивлению материалов на тему растяжение-сжатие.
Учет собственного веса в задачах сопротивления материалов на растяжение-сжатие
видео урок — Учет собственного веса в задачах сопротивления материалов на растяжение-сжатие
Третья задача на растяжение-сжатие стержней с учетом собственного веса. Приведен пример решения задачи и доступно рассказывается как можно учесть собственный вес конструкции при расчете на растяжение-сжатие.
Растяжение-сжатие с учетом собственного веса в стержнях с двумя участками
Задача на растяжение сжатие, более сложный случай. В этой задаче стержень состоит из нескольких участков. Здесь необходимо учитывать собственный вес — для стержня, испытывающего деформацию растяжения или сжатия, который состоит из нескольких участков. Здесь же приводится методика построения эпюр внутренних усилий при этих видах деформации.
Удлинение стержня при деформации растяжения-сжатия
видео урок — Удлинение стержня при деформации растяжения-сжатия
Приведен пример расчета на растяжение-сжатие когда нужно определить удлинение стержня. Удлинение (при растяжении) или укорочение (при сжатии) — это изменение размеров стержня вдоль оси приложения продольной нагрузки. Об этом в пятом видео уроке.
Определение удлинения стержня с учетом собственного веса при растяжении-сжатии
Определение изменения длины стержня с учетом собственного веса. Особенности формулы для определения удлинения (изменения длины) при растяжении-сжатии с учетом собственного веса.
Итак на этой странице приведены видеоуроки на основные темы в растяжении-сжатии. Планируется запись еще темы в которой будут рассматриваться статически неопределимые задачи на растяжение-сжатие.
Конечно это не все задачи, которые может понадобиться решить реальному инженеру, как инженеру-механику, так и инженеру-строителю. Встречаются разные случаи, когда нужно применять сообразительность.
Метод сечений в задачах на растяжение сжатие
Однако подход в решении всех задач на растяжение-сжатие всегда одинаков и состоит из следующих шагов:
- рассекаем наш стержень (а именно так называют элемент конструкции, который испытывает деформацию растяжения-сжатия)
- рассматриваем равновесие одной из частей стержня рассматривая внешние, приложенные к стержню усилия и внутреннее усилие, которое формируется силами межатомного взаимодействия
- внутреннее усилие направляем от сечения рассматриваемой части стержня к оставшейся части стержня (для статически определимых систем) или используя интуицию и опыт направляем так, чтобы направление внутреннего усилия совпало с направлением действия деформации (на растяжение или на сжатие)
- из суммы проекций на соответствующую ось или, если это возможно, суммы моментов относительно точки находим нужное внутреннее усилие.
В статически неопределимой задаче нужно к указанным действиям добавить еще одно уравнение которое называется деформационным.
Растяжение-сжатие в сопротивлении материалов одна из наиболее простых тем, разнообразие задач, правда, довольно широко. Но именно растяжение-сжатие в сопротивлении материалов учит тому, как нужно правильно и везде одинаково, несмотря на разнообразие расчетных схем, применять один и тот же подход к решению — метод сечений. В классическом курсе сопротивления материалов это первая тема — растяжение-сжатие.
список видео уроков по сопромату в котором темы раскрываются одна за другой. рекомендую для изучения сопромата
Ну а если возникнут сложности, если Вы предпочитаете заниматься индивидуально — обратитесь ко мне — помогу!
skype: zabolotnyiAN,
e-mail: zabolotnyiAN@gmail.com
Остались вопросы?
Все вопросы, которые у Вас могут возникнуть — рассмотрены в рубрике Условия и цена онлайн обучения сопромат и строймех. Для связи со мной используйте страницу «Контакты» или всплывающий внизу справа значок мессенджера.
Рубрики
Задачи по сопротивлению материалов с решениями, примеры, Растяжение — сжатие, Сопромат онлайн
Метки
внутренние усилия, задачи курса сопротивление материалов, классический курс сопротивления материалов в решениях задач, краткий курс сопротивления материалов, курс сопромата для чайников, Построение эпюр продольных сил, растяжение сжатие сопромат, растяжение сжатие сопротивление материалов, сопромат для чайников, Сопромат Примеры решения задач на растяжение-сжатие, сопромат репетитор, Сопромат это легко, Сопротивление материалов, сопротивление материалов краткий курс, сопротивление материалов примеры решения задач, эпюры растяжения сжатия
Источник
Построение эпюр продольных сил – это решение статически определимой задачи. Производится для выявления картины нагрузки упругого тела. Вернее, уточнения ее схематизации.
Необходимо для определения наиболее напряженного, так называемого «опасного» сечения. Затем методами сопромата (сопротивления материалов) проводится анализ с прогнозированием перемещений элементов конструкции.
Но всему свое время. Сначала немного о терминах.
Основные понятия
Брусом (балкой) называют тело, вытянутое вдоль оси. То есть длина преобладает над шириной и высотой.

Если имеются только осевые (продольные) силы, то объект подвергается растяжению/сжатию. В этом случае в материале возникают только нормальные поперечному сечению силы противодействия и тело считают стержнем.
Статическая определимость подразумевает достаточность схемы для установления внутренних усилий противодействия. Участок – часть балки с неизменным сечением и характерной нагрузкой.
Правила построения учитывают знаки усилий. Растягивающие принимают положительными, сжимающие – отрицательными.
В системе СИ силы измеряются в ньютонах (Н). Длины в метрах (м).
Что такое эпюра продольных сил
Показывает, какой силой (в нашем предположении нормальной) загружен каждый участок. По всей длине стержня. Иначе говоря, эпюра – наглядное графическое изображение изменения нагрузки по всей длине конструкции.
Как построить эпюру продольных сил
Используется метод сечений. Балка виртуально рассекается на каждом участке и ищется противодействующая N. Ведь задача статическая.
Сопротивление рассчитывается по формуле:
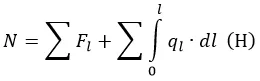
где:
Fl – действующие на участке l силы (Н);
ql – распределенные нагрузки (Н/м).
Порядок построения:
1. Рисуется схема балки и механизмов закрепления;
2. Производится разделение на участки;
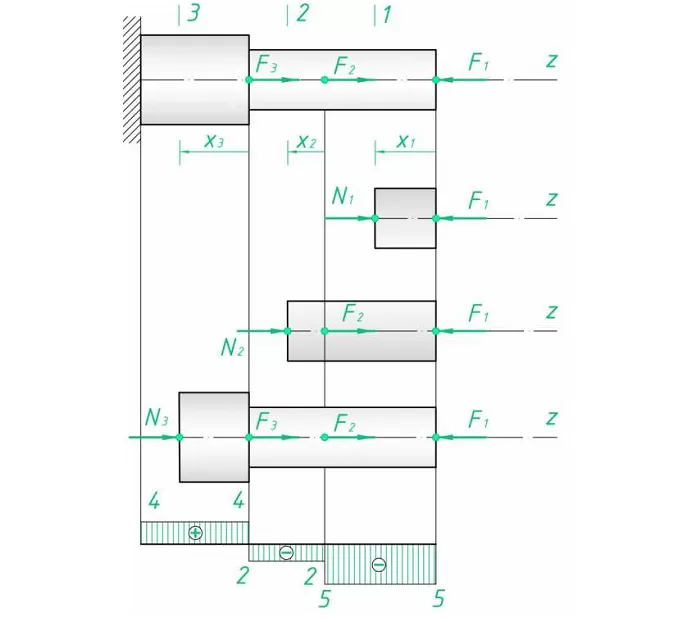
3. Для каждого рассчитывается N с учетом знаков. Если у балки есть незакрепленный конец, то начинать удобнее именно с него. В противном случае считается реакция опор. И оптимальнее выбирать сечение с меньшим количеством действующих факторов:
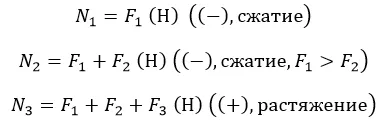
Нетрудно заметить, что последнее уравнение дает еще и реакцию опоры;
4. Параллельно оси стержня намечается база эпюры. Положительные значения масштабировано проставляются выше, отрицательные – ниже. Эпюру наглядно совмещать с расчетной схемой. Итоговый результат и промежуточные сечения показаны на рис. 1.

Рис. 1. Эпюра продольных сил
Рассмотрим случай:
F1 = 5 (кН);
F2 = 3 (кН);
F3 = 6 (кН).
Вычислим:
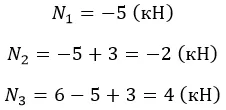
Проверить эпюру можно по скачкам: изменения происходят в точках приложения сил на их величину.
Пример построения эпюр и решения задач
Построить эпюру сил для следующего случая (рис. 2):
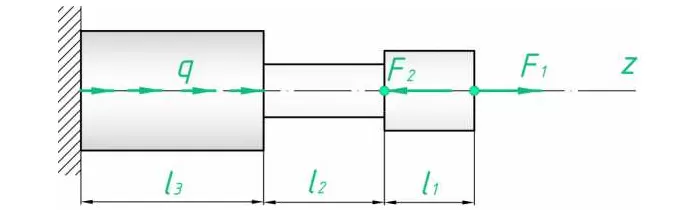
Рис. 2
Дано:
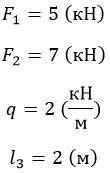
Решение.
Разбиение на участке вполне очевидно. Найдем сопротивление на выделенных:
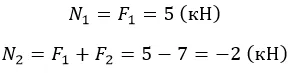
Распределенная нагрузка зависит от длины, на которой приложена. Поскольку нарастает линейно, значение N2 будет постепенно увеличиваться/уменьшаться в зависимости от знака q.
Эпюра такого вида усилия представляет собой прямоугольный треугольник с катетами l3 и ql3 (в масштабе). Поскольку распределение линейно.
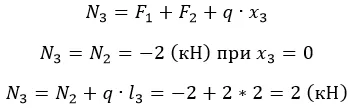
По полученным данным строим эпюру (рис. 3).
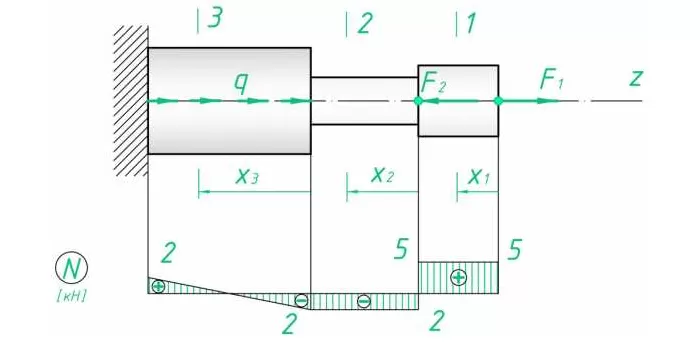
Рис. 3
Заключение
Приведенный алгоритм является предварительным этапом в расчете модели на прочность. «Слабое» место находится уже с учетом площади поперечного сечения.
В сети имеются онлайн сервисы для помощи в расчетах при вычерчивании. Но стоит ли ими пользоваться, если процедура настолько проста? Если не запутаться в знаках, конечно. Это самая распространенная ошибка.
Источник
+- мdA
площадь сечения стержняZB м м м м м м м м м м м м м м м м м м м м м м м м м м м м мL=2(м)N[кН]
Продольная сила N,кН0σ [МПа]
Напряжения ,МПа0δ [мм]
Перемещения характерных сечений ,мм0
Модуль упругости E=
ГПа (сталь)
Выбрать из таблицы
Длина стержня l=
м.
Площадь A= = 0.0004 м2
Выбрать тип сечения исходя из условий задачи
Круг
Квадрат
Прямоугольник
Шестигранник
Кольцевое сечение (труба)
Площадь сечения в см2:
A = π · d2/4
= 3.14·(d·0.1)2/4 =
[см2]
Масса 1 м профиля, [кг]:
m = ρ·A·L =
7850· A ·1/10000 = [кг]
ДСТУ 4738:2007/ГОСТ 2590-2006 Прокат сортовой стальной горячекатаный круглый.
(При вычислении массы 1 м проката плотность стали принята равной 7850 кг/м3)
Выбрать диаметр из сортамента:
| Диаметр d, мм | |||||||||||||||||||
| 5 | 5.5 | 6 | 6.3 | 6.5 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 |
| 42 | 43 | 44 | 45 | 46 | 47 | 48 | 50 | 52 | 53 | 54 | 55 | 56 | 58 | 60 | 62 | 63 | 65 | 67 | 68 |
| 70 | 72 | 73 | 75 | 78 | 80 | 82 | 85 | 87 | 90 | 92 | 95 | 97 | 100 | 105 | 110 | 115 | 120 | 125 | 130 |
| 135 | 140 | 145 | 150 | 155 | 160 | 165 | 170 | 175 | 180 | 185 | 190 | 195 | 200 | 210 | 220 | 230 | 240 | 250 | 260 |
| 270 | |||||||||||||||||||
ДСТУ ГОСТ 1535:2007/ГОСТ 1535-2006 Прутки медные
(При вычислении массы 1 м проката плотность меди принята равной 8900 кг/м3)
Выбрать диаметр из сортамента:
| Номинальный диаметр d, мм | |||||||||||||||||||
| 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 24 | 25 | 27 | 28 | 30 | 32 | 33 | 35 | 36 | 38 | 40 | 41 | 45 | 46 | 50 | ||
| Номинальный диаметр d, мм | |||||||||||||||||||
| 20 | 22 | 25 | 28 | 30 | 32 | 35 | 38 | 40 | 42 | 45 | 48 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 |
| 90 | 95 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | |||||||||
ДСТУ ГОСТ 2060:2007/ГОСТ 2060-2006 Прутки латунные
(При вычислении массы 1 м проката плотность латуни принята равной 8500 кг/м3)
Выбрать диаметр из сортамента:
| Номинальный диаметр d, мм | |||||||||||||||||||
| 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | 9 | 9.5 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 30 | 32 | 35 | 36 | 38 | 40 | 41 |
| 42 | 45 | 46 | 48 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 | 110 | 120 | 130 | 140 | 150 |
| 160 | 170 | 180 | |||||||||||||||||
ГОСТ 21488-97 Прутки прессованные из алюминия и алюминиевых сплавов
(При вычислении массы 1 м проката плотность алюминия принята равной 2700 кг/м3)
Выбрать диаметр из сортамента:
| Номинальный диаметр d, мм | |||||||||||||||||||
| 8 | 10 | 12 | 14 | 16 | 18 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 90 |
| 100 | 110 | 120 | 130 | 140 | 150 | 160 | 180 | 200 | 250 | 300 | 350 | 400 | |||||||
ГОСТ 26492-85 Прутки катаные из титана и титановых сплавов
(При вычислении массы 1 м проката плотность титана принята равной 4500 кг/м3)
Выбрать диаметр из сортамента:
| Номинальный диаметр d, мм | |||||||||||||||||||
| 10 | 12 | 14 | 16 | 18 | 20 | 22 | 25 | 28 | 30 | 32 | 35 | 38 | 40 | 42 | 45 | 48 | 50 | 52 | 55 |
| 60 | 65 | 70 | 75 | 80 | 85 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | |||||||
ТУ 48-19-39-85 Прутки вольфрамовые
(При вычислении массы 1 м проката плотность титана принята равной 19300 кг/м3)
Выбрать диаметр из сортамента:
| Номинальный диаметр d, мм | |||||||||||||||||||
| 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | 9 | 9.5 | 10 | 10.5 | 11 | 11.5 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | |||||||||||||||
ТУ 48-19-247-87 Прутки молибденовые диаметром от 16 до 125 мм
(При вычислении массы 1 м проката плотность молибдена принята равной 10188 кг/м3)
Выбрать диаметр из сортамента:
| Номинальный диаметр d, мм | |||||||||||||||||||
| 16 | 17 | 18 | 19 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 | 42 | 44 | 46 | 48 | 50 |
| 52 | 54 | 56 | 58 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 | 105 | 110 | 115 | 120 | 125 | ||
ГОСТ 13083-2016 Прутки из никеля и кремнистого никеля
(При вычислении массы 1 м проката плотность никеля принята равной 8900 кг/м3)
Выбрать диаметр из сортамента:
| Номинальный диаметр d, мм | |||||||||||||||||||
| 5 | 5.5 | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | 9 | 9.5 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 30 | 32 | 34 | 36 | 38 | 40 | |||||
| Номинальный диаметр d, мм | |||||||||||||||||||
| 42 | 45 | 48 | 50 | 55 | 60 | 70 | 80 | 90 | |||||||||||
a
Площадь сечения в см2:
A = a2 = (a·0.1)2 =
[см2]
Масса 1 м профиля, [кг]:
m = ρ·A·L =
7850· A ·1/10000 = [кг]
(При вычислении массы 1 м проката плотность стали принята равной 7850 кг/м3)
ДСТУ 4746:2007/ГОСТ 2591-2006 Прокат сортовой стальной горячекатаный квадратный.
Выбрать размер из сортамента:
DAs
D=s/2 + (2A)/(πs)
Толщина стенки трубы s=
мм
Нормальные линейные размеры (диаметры, длины, высоты и др.) должны выбираться в соответствии с таблицей
(размеры в мм)
Выбрать размер из таблицы:
| Ra5 | |||||||||||||||||||
| 0,1 | 0,4 | 0,63 | 1,0 | 1,6 | 2,5 | 4,0 | 6,3 | 10,0 | 16,0 | 25 | 40 | 63 | 100 | 160 | 250 | 400 | 630 | 1000 | 1600 |
| Ra10 | |||||||||||||||||||||||||||||
| 0,1 | 0,2 | 0,4 | 0,5 | 0,63 | 0,8 | 1,0 | 1,2 | 1,6 | 2,0 | 2,5 | 3,2 | 4,0 | 5,0 | 6,3 | 8,0 | 10 | 12 | 16 | 20 | 25 | 32 | 40 | 50 | 63 | 80 | 100 | 125 | 160 | 200 |
| 250 | 320 | 400 | 500 | 630 | 800 | 1000 | 1250 | 1600 | 2000 | ||||||||||||||||||||
| Ra20 | |||||||||||||||||||||||||||||
| 0,1 | 0,2 | 0,4 | 0,5 | 0,63 | 0,71 | 0,8 | 0,9 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 | 2,5 | 2,8 | 3,2 | 3,6 | 4,0 | 4,5 | 5,0 | 5,6 | 6,3 | 7,1 | 8,0 | 9,0 | 10 | 11 | 12 |
| 14 | 16 | 20 | 22 | 25 | 28 | 32 | 36 | 40 | 45 | 50 | 56 | 63 | 71 | 80 | 90 | 100 | 110 | 125 | 140 | 160 | 180 | 200 | 220 | 250 | 280 | 320 | 360 | 400 | 450 |
| 500 | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 | 1800 | 2000 | |||||||||||||||||
| Ra40 | |||||||||||||||||||||||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,63 | 0,71 | 0,8 | 0,9 | 1,0 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 | 2,1 | 2,2 | 2,4 | 2,5 | 2,6 | 2,8 | 3,0 | 3,2 | 3,4 | 3,6 | 3,8 |
| 4,0 | 4,2 | 4,5 | 4,8 | 5,0 | 5,3 | 5,6 | 6,0 | 6,3 | 6,7 | 7,1 | 7,5 | 8,0 | 8,5 | 9,0 | 9,5 | 10,0 | 10,5 | 11,0 | 11,5 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 24 | 25 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 | 42 | 45 | 48 | 50 | 53 | 56 | 60 | 63 | 67 | 71 | 75 | 80 | 85 | 90 | 95 | 100 | 105 | 110 | 120 |
| 125 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 | 210 | 220 | 240 | 250 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 | 420 | 450 | 480 | 500 | 530 | 560 | 600 | 630 | 670 |
| 710 | 750 | 800 | 850 | 900 | 950 | 1000 | 1060 | 1120 | 1180 | 1250 | 1320 | 1400 | 1500 | 1600 | 1700 | 1800 | 2000 | ||||||||||||
| Дополнительные размеры | |||||||||||||||||||||||||||||
| 2,3 | 2,7 | 2,9 | 3,1 | 3,3 | 3,5 | 3,7 | 3,9 | 4,1 | 4,4 | 4,6 | 4,9 | 5,2 | 5,5 | 5,8 | 6,2 | 6,5 | 7,0 | 7,3 | 7,8 | 8,2 | 8,8 | 9,2 | 9,8 | 10,2 | 10,8 | 11,2 | 11,8 | 12,5 | |
| 13,5 | 14,5 | 15,5 | 16,5 | 17,5 | 18,5 | 19,5 | 20,5 | 21,5 | 23 | 27 | 29 | 31 | 33 | 35 | 37 | 39 | 41 | 52 | 55 | 58 | 65 | 70 | 73 | 78 | 82 | 88 | 92 | 98 | |
| 102 | 108 | 112 | 115 | 118 | 135 | 145 | 155 | 165 | 175 | 185 | 195 | 205 | 215 | 230 | 270 | 290 | 310 | 315 | 330 | 350 | 370 | 390 | 410 | 440 | 460 | 490 | 515 | 545 | |
| 580 | 615 | 650 | 690 | 730 | 775 | 825 | 875 | 925 | 975 | 1030 | 1090 | 1150 | 1220 | 1280 | 1360 | 1450 | 1550 | 1650 | 1750 | 1850 | 1950 | ||||||||
1) При выборе размеров предпочтение должно отдаваться рядам с более крупной градацией
(ряд Ra5 – ряду Ra10, ряд Ra10 – ряду Ra20, ряд Ra20 – ряду Ra40).
2) Дополнительные размеры допускается применять лишь в отдельных, технически обоснованных случаях.
Кол-во сил F, действующих на стержень:
Длина — расстояние прилагаемой нагрузки от заделки:
Источник
