Растяжение и сжатие графиков вдоль оси абсцисс
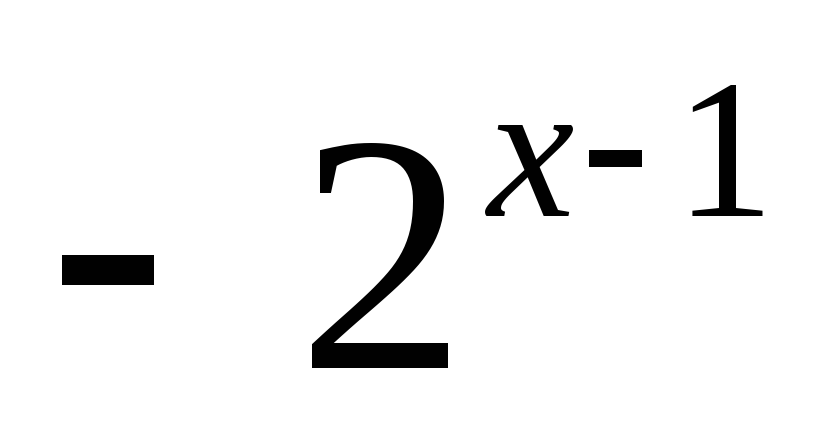
Ìàñøòàáèðîâàíèå — îïåðàöèÿ ñæàòèÿ èëè ðàñòÿæåíèÿ ãðàôèêà ôóíêöèè âäîëü îñåé àáñöèññ è îðäèíàò.
Òî, ÷òî òðåáóåòñÿ âûïîëíèòü ìàñøòàáèðîâàíèå, ïîêàçûâàþò êîýôôèöèåíòû k1 è k2 â óðàâíåíèè y = ± k1 f (± k2 (x + a))+b. Îíè äîëæíû áûòü íå ðàâíû åäèíèöå.
Êîãäà 0 < k1,2 <1, ñîâåðøàåì ñæàòèå ãðàôèêà îòíîñèòåëüíî y è ðàñòÿæåíèå îòíîñèòåëüíî x , êîãäà k1,2>1, âûïîëíÿåì ðàñòÿæåíèå âäîëü îñè îðäèíàò è ñæàòèå âäîëü îñè àáñöèññ.
Êîãäà ôóíêöèÿ ïðèíèìàåò âèä y = f (k2x) ,òî åñëè k2 >1 – ïðîèçâîäèì ñæàòèå ãðàôèêà ê îñè îðäèíàò (y) â k ðàç, à åñëè 0 < k2<1 — ðàñòÿæåíèå ãðàôèêà îò îñè îðäèíàò â 1/k.
Êîãäà ôóíêöèÿ ïðèíèìàåò âèä y = k1 f (x) , òî åñëè k1 >1 — îñóùåñòâëÿåì ðàñòÿæåíèå ãðàôèêà îò îñè àáñöèññ (0x) â k ðàç, à åñëè 0 < k1<1 — ñæàòèå ãðàôèêà ê îñè àáñöèññ â 1/k.
Êàëüêóëÿòîðû ïî àëãåáðå | |
| Ðåøåíèÿ, ïîäñêàçêè è ó÷åáíèê ëèíåéíîé àëãåáðû îíëàéí (âñå êàëüêóëÿòîðû ïî àëãåáðå). | |
| Êàëüêóëÿòîðû ïî àëãåáðå | |
Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû | |
| Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû: êîðíè, äðîáè, ñòåïåíè, óðàâíåíèÿ, ôèãóðû, ñèñòåìû ñ÷èñëåíèÿ è äðóãèå êàëüêóëÿòîðû. | |
| Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû | |
Àëãåáðà 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó àëãåáðû äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Àëãåáðà 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
Ãðàôèêè ýëåìåíòàðíûõ ôóíêöèé | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó ìàòåìàòèêè äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Ãðàôèêè ýëåìåíòàðíûõ ôóíêöèé | |
Ôóíêöèÿ. Ïîêàçàòåëüíàÿ ôóíêöèÿ. | |
| Ïîêàçàòåëüíîé íàçûâàåòñÿ ôóíêöèÿ ó = à õ , â êîòîðîé à ýòî ïîñòîÿííîå ïîëîæèòåëüíîå ÷èñëî. | |
| Ôóíêöèÿ. Ïîêàçàòåëüíàÿ ôóíêöèÿ. | |
Ôóíêöèÿ. Ëèíåéíûå ôóíêöèè. | |
| Åñëè ïåðåìåííûå õ, ó âûðàæàþòñÿ ïîñðåäñòâîì óðàâíåíèÿ Àõ + By = Ñ , ïðè ýòîì ÷èñëà À,  èëè ïî ìåíüøåé ìåðå îäíî èç íèõ, íå ðàâíî íóëþ, òî ãðàôèêîì ôóíêöèîíàëüíîé çàâèñèìîñòè ÿâëÿåòñÿ ïðÿìàÿ ëèíèÿ . | |
| Ôóíêöèÿ. Ëèíåéíûå ôóíêöèè. | |
Источник
3.1 Сжатие (растяжение) графика вдоль оси ординат
Рассмотрим
функцию вида y=A
,
где A>0.
Нетрудно заметить, что при равных
значениях аргумента ординаты графика
этой функции будут в A
раз больше ординат графика функции
y=f(x)
при A>1
или в
раз меньше ординат графика функцииy=f(x)
при A<1.
Таким образом, получаем следующее
правило.
Для
построения графика функции y=A
следует построить график функции y=f(x)
и увеличить его ординаты в A
раз при A>1
(произвести растяжение графика вдоль
оси ординат) или уменьшить его ординаты
в
раз приA<1
(произвести сжатие графика вдоль оси
ординат). Полученный график является
графиком функции y=A
.
Пример
13. Построить
график функции y=2cos
x.
Р
е ш е н и е: Строим график функции y=cos
x
(рис.16 – пунктирная кривая) и растяжением
этого графика вдоль оси ординат в 2
раза получаем график функции y=2cos
x
(сплошная кривая).
Пример
14. Построить
график функции y=
x2.
Р
е ш е н и е: Строим график функции y=x2
и сжатием этого графика в 3 раза вдоль
оси ординат получаем график функции
y=
x2
(рис.17).
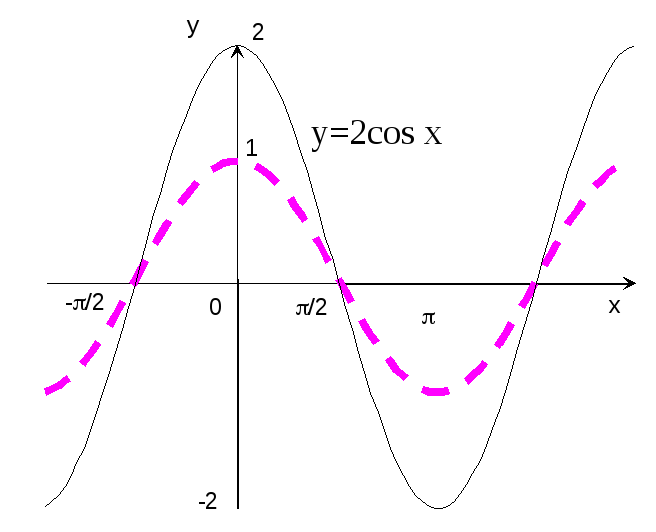
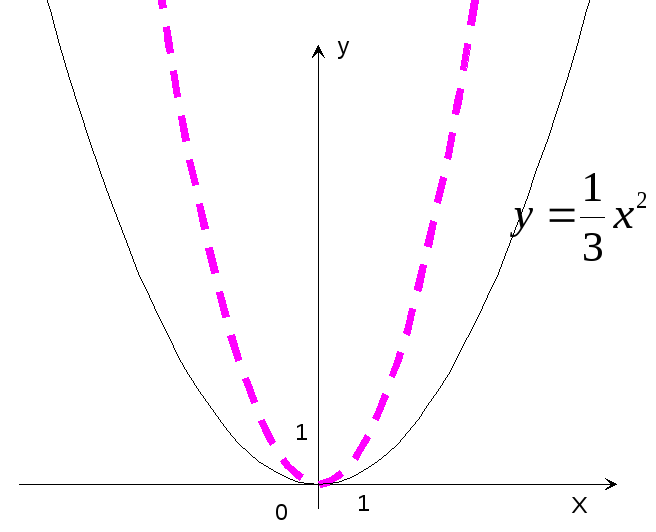
Рис.16
Рис.17
3.2. Сжатие (растяжение) графика вдоль оси абсцисс
Пусть
требуется построить график функции
y=f(x),
где >0.
Рассмотрим функцию y=f(x),
которая в произвольной точке x=x1
принимает значение y1=f(x1).
Очевидно,
что функция y=f(x)
принимает такое же значение в точке
x=x2,
координата
к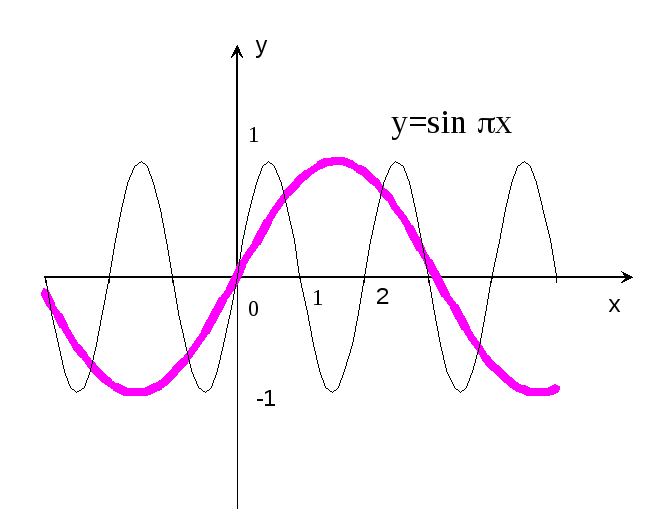
оторой
определяется равенствомx1=x2,
или x2=
,
причём это равенство справедливо для
совокупности всех значений x
из области определения функции.
Следовательно, график функции y=f(x)
оказывается сжатым (при >1)
или растянутым (при <1)
вдоль оси абсцисс относительно графика
функции y=f(x).
Таким образом, получаем следующее
правило.
Для
построения графика функции y=f(x)
следует построить график функции y=f(x)
и уменьшить его абсциссы в
раз при >1
(произвести сжатие графика вдоль оси
абсцисс) или увеличить его абсциссы в
раз при<1
(произвести растяжение графика вдоль
оси абсцисс). Полученный график является
графиком функции y=f(x).
П
Рис. 18
ример 15.Построить
график функции
x.
Р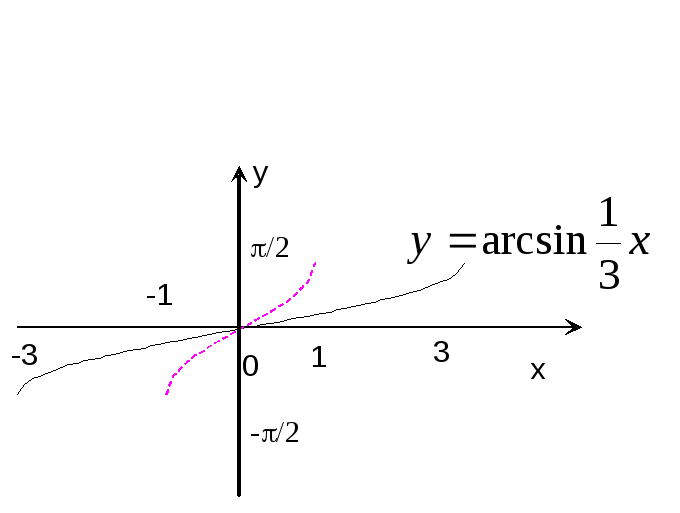
е ш е н и е: Строим график функции
x
(рис.18 – пунктирная кривая), и проводя
его сжатие в
раз вдоль оси абсцисс, получаем график
функции
x
(сплошная кривая). Период этой функции
уже равен не 2,
а
=2.
График пересекает ось абсцисс в точкахx=0,
…
.
Пример
16. Построить
график функции
.
Р
е ш е н и е: Строим график функции
и, растянув его вдоль оси абсцисс в 3
раза, получаем график функции
.
4. Комбинация переноса, отражения и деформации
Рис.
19
Очень часто при построении графиков
функций применяют композицию приёмов,
изложенных в пунктах 1-3. Последовательное
применение ряда таких приёмов позволяет
существенно упростить построение
графика исходной функции и нередко
свести его в конце концов к построению
одной из простейших элементарных
функций.
Рассмотрим,
как с учётом изложенного следует,
например, построить
график функции вида y=Af(x+a)+b.
Запишем
исходную функцию в виде y=Af
[
( x+
) ] +b
и схему поэтапного её упрощения
(последовательность преобразований):
1
.y=Af
[
( x+
) ] + b
; перенос оси абсцисс на b
единиц;
2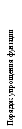
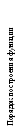
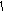.y=Af
[
( x+
) ]; перенос оси ординат на
единиц;
3. y=Af
[
x
]; отражение графика относительно оси
абсцисс
(
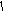этап
выполняется только приA<0);
4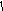
.y=A·
f
(x); сжатие
или растяжение графика
вдоль оси ординат;
5. y=f
(x) отражение
графика относительно оси ординат
(
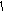этап
выполняется только при<0);
6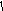
.y=f
(
x); сжатие
или растяжение вдоль оси абсцисс;
7. y=f
( x);
Проводя
построение графика шаг за шагом в
порядке, обратном порядку упрощения
вида функции с учётом всех указанных
правил, получим график исходной функции.
Пример 17. Построить
график функции y=
.
Р
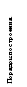е ш е н и е: Схема построения графика :
y
=
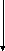
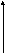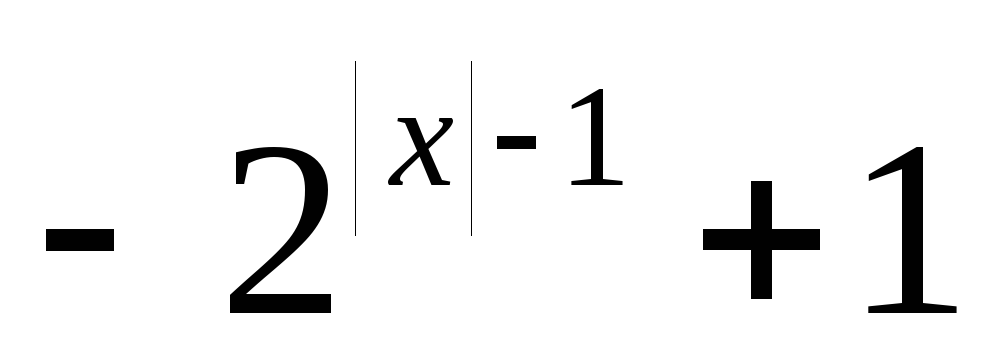
x
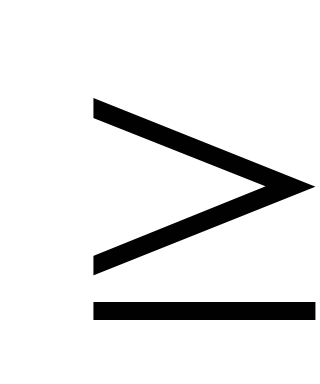0,
y=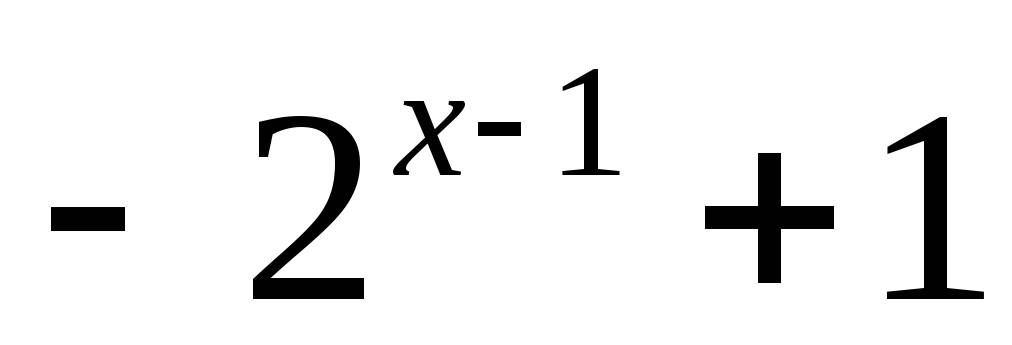
;y=
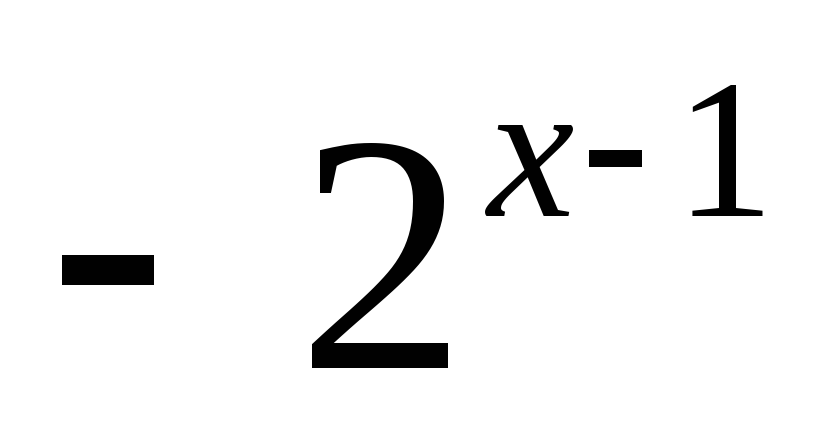;у=
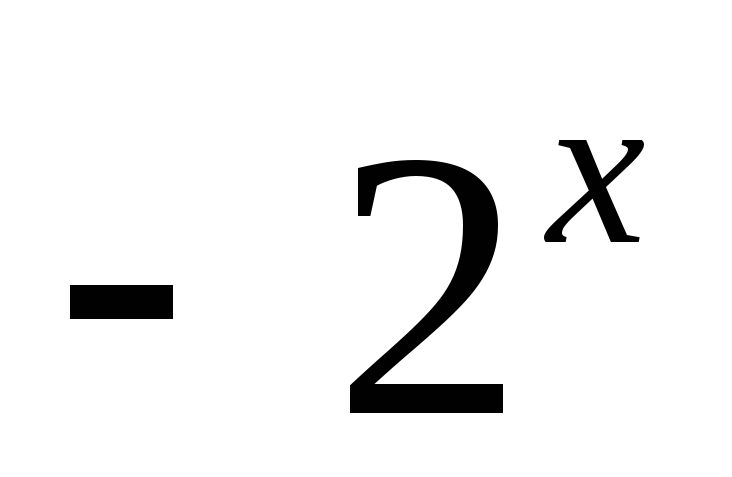;y=
;
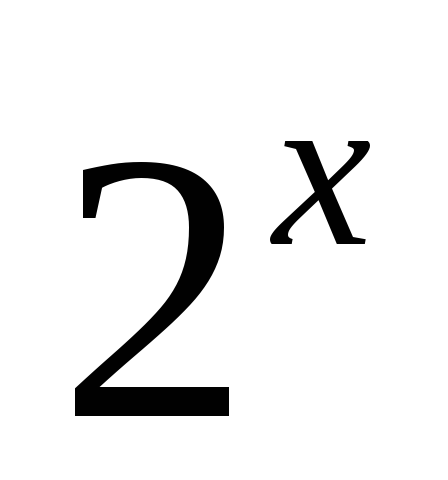Итак,
построение графика исходной функции
следует начинать с построения графика
функции y=
.
График (рис.20) пересекает ось ординат
в точке
(из условияx=0),
а ось абсцисс в точках x=1
(из условия y=0,
т.е.
=0).
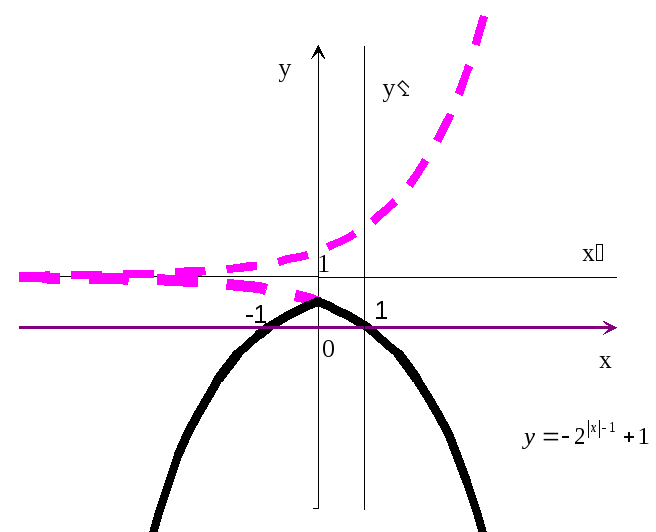В
заключении отметим, что порядок упрощения
целесообразно проводить в следующей
последовательности.
Использование
чётности или нечётности функции.Перенос осей.
Отражение и
деформация.
Построение
же графика, как обычно, выполняется в
обратной последовательности.
Рис.20
Задание для
самостоятельного выполнения
Ниже
приводятся тексты заданий для
самостоятельного выполнения. Вам
необходимо построить графики функций,
оформить работу отдельно от решений по
другим предметам и выслать в адрес
Хабаровской краевой заочной
физико-математической школы.
М.11.2.1 С
помощью элементарных преобразований
постройте графики следующих функций:
y=x2-2;
y=(x+1)2;
y=sin
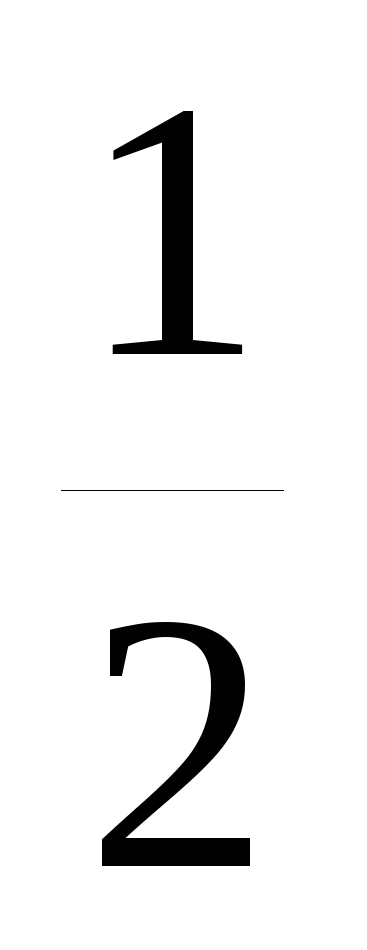x;y=-
3sin x;y=tg
;
М.11.2.2.
Написать последовательность преобразований
и построить графики следующих функций:
y=
;y=(x-1)3+2;
y=ln
(1-x);y=tg(-
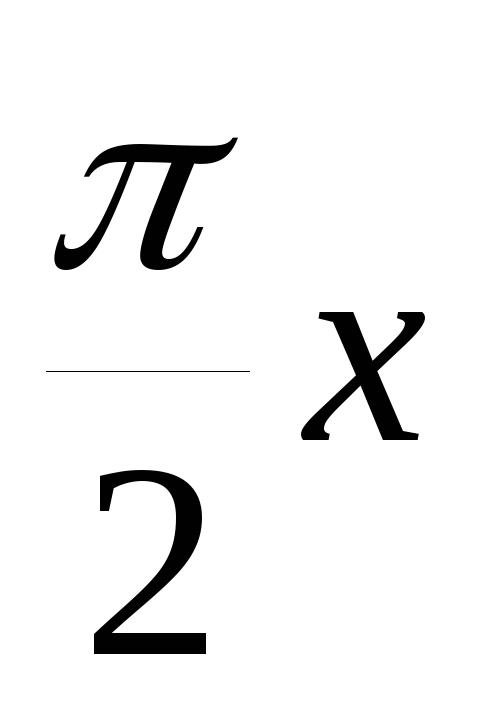);y=
cos(2x-1)-2.
Хабаровская краевая заочная
физико-математическая школа
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Анна Малкова
В этой статье мы расскажем об основных преобразованиях графиков функций. Что нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали. Как задать растяжение графика по горизонтали или вертикали. Как отразить график относительно оси Х или Y.
Очень жаль, что эта тема — полезная и очень интересная — выпадает из школьной программы. На нее не постоянно хватает времени. Из-за этого многим старшеклассникам не даются задачи с параметрами — которые на самом деле похожи на конструктор, где вы собираете решение из знакомых элементов. Хотя бы для того, чтобы решать задачи с параметрами, стоит научиться строить графики функций.
Но конечно, не только для того, чтобы сдать ЕГЭ. Первая лекция на первом курсе технического или экономического вуза посвящена функциям и графикам. Первые зачеты в курсе матанализа связаны с функциями и графиками.
Начнем со сдвигов графиков по Х и по Y.
Сдвиг по горизонтали.
Пусть функция задана формулой и Тогда график функции сдвинут относительно исходной на а вправо. График функции сдвинут относительно исходной на а влево.
1. Сдвиг по вертикали.
Пусть функция задана формулой и С — некоторое положительное число. Тогда график функции сдвинут относительно исходного на С вверх. График функции сдвинут относительно исходного на С вниз.
Теперь растяжение графика. Или сжатие.
2. Растяжение (сжатие) по горизонтали.
Пусть функция задана формулой и Тогда график функции растянут относительно исходного в k раз по горизонтали, если , и сжат относительно исходного в k раз по горизонтали, если
3. Растяжение (сжатие) по вертикали
Пусть функция задана формулой и Тогда график функции растянут относительно исходного в М раз по вертикали, если , и сжат относительно исходного в М раз по вертикали, если
И отражение по горизонтали.
4. Отражение по горизонтали
График функции симметричен графику функции относительно оси Y.
5. Отражение по вертикали.
График функции симметричен графику функции относительно оси Х.
Друзья, не возникло ли у вас ощущения, что вы все это где-то видели? Да, наверняка видели, если когда-либо редактировали изображения в графическом редакторе на компьютере. Изображение можно сдвинуть (по горизонтали или вертикали). Растянуть (по горизонтали или вертикали). Отразить. И все это мы делаем с графиками функций.
И еще два интересных преобразования. Здесь в формулах присутствует знак модуля. Если не помните, что такое модуль, — срочно повторите эту тему.
6. Графики функций и
На рисунке изображен график функции Она специально взята такая — несимметричная относительно нуля.
Построим график функции
Конечно же, мы пользуемся определением модуля.
Это мы и видим на графике. Для неотрицательных значений х график остался таким же, как был. А вместо каждого отрицательного х мы взяли противоположное ему положительное число. И поэтому вся та часть графика функции, что лежала слева от оси Х, заменилась на зеркально отраженную правую часть графика.
Теперь график функции Вы уже догадались, что будет. Вся часть графика, лежащая ниже оси Х, зеркально отражается в верхнюю полуплоскость. А верхняя часть графика, лежащая выше оси Х, остается на месте.
Как определить по формуле функции, будет график преобразован по горизонтали (по Х) или по вертикали (по Y)? Разница очевидна. Если сначала мы что-либо делаем с аргументом х (прибавляем к нему какое-либо число, умножаем на какое-либо число или берем модуль) — преобразование по Х. Если сначала мы нашли функцию, а затем уже к значению функции что-то прибавили, или на какое-нибудь число умножили, или взяли модуль, — преобразование по Y.
Вот самые простые задачи на преобразование графиков.
1. Построим график функции
Это квадратичная парабола, сдвинутая на 3 влево по x и на 1 вниз по y.
Вершина в точке
2. Построим график функции
Выделим полный квадрат в формуле.
График — квадратичная парабола, сдвинутая на 2 вправо по x и на 5 вниз по y.
Обратите внимание: график функции пересекает ось y в точке На нашем графике это точка
Продолжение — в статье «Построение графиков функций».
Источник
Преобразования
графиков функций – это линейные преобразования функции y
= f(x) или её аргумента х к виду
y
= af(kx
+ b) + m,
а так же
преобразование с использованием модуля.
Зная,
как строить графики функции y =
f(x), где
y
= kx + b,
y
= ax2,
y
= xn,
y
= k/x,
y
= ax,
y
= logax,
можно
построить график функции
y
= af(kx
+ b) + m.
ОБЩИЙ ВИД ПРЕОБРАЗОВАНИЯ ФУНКЦИИ
Параллельный
перенос графика вдоль оси абсцисс на |b| единиц.
y
= f(x–
b)
вправо,
если b ˃ 0;
влево,
если b < 0.
y
= f(x+
b)
влево,
если b ˃ 0;
вправо,
если b < 0.
ПРИМЕР:
Построить график функции
у =
(х + 2)3.
Построим график функции у =
х3 и
параллельно перенесём его влево на 2 единицы вдоль оси х (так как 2 ˃ 0). Получим график
функции
у = (х + 2)3.
ПРИМЕР:
Построить график функции
у =
(х – 3)2.
Построим график функции у =
х2 и
параллельно перенесём его вправо на 3 единицы вдоль оси х (так как –3 < 0). Получим график
функции
у =
(х – 3)2.
Параллельный
перенос графика вдоль оси ординат на |m| единиц.
y
= f(x) + m
вверх,
если m ˃ 0;
вниз,
если m < 0.
ПРИМЕР:
Построить график функции
у =
х2 – 5.
Построим график функции у =
х2 и
параллельно перенесём его вниз на 5 единиц вдоль оси у (так как –5 < 0). получим график
функции
у =
х2 – 5.
ПРИМЕР:
Построить график функции
у =
√͞͞͞͞͞х + 4.
Построим график функции у =
√͞͞͞͞͞х и параллельно перенесём его вверх на 4 единицы
вдоль оси у (так как
4 ˃ 0). Получим график функции
у =
√͞͞͞͞͞х + 4.
Отражение
графика.
y
= f(–x)
Симметричное
отражение графика относительно оси ординат.
ПРИМЕР:
Построить график функции
у =
–х + 3.
Построим график функции у =
х + 3 и отобразим
полученный график симметрично относительно оси
у и получим график
функции
у =
–х + 3
y
= –f(x)
Симметричное
отражение графика относительно оси абсцисс.
ПРИМЕР:
Построить график функции
у =
–(х – 3)2.
Построим график функции у =
х2 и
параллельно перенесём его вправо на 3 единицы вдоль оси х (так как –3 < 0). получим график
функции
у =
(х – 3)2.
отобразим полученный график симметрично относительно
оси х и получим
график функции
у =
–(х – 3)2.
Сжатие
и растяжение графика.
y
= f(kx)
При k ˃ 1 –
сжатие графика к оси ординат в k раз,
при 0 < k<
1 – растяжение графика от оси ординат в k раз,
ПРИМЕР:
Построить график функции
у =
(3х)2.
Построим график функции у =
х2. Выполним
сжатие графика функции в три раза до оси у и получим
график функции
у =
(3х)2.
ПРИМЕР:
Построить график функции
Построим график функции у =
√͞͞͞͞͞х. Выполним
растяжение графика функции в 1/3 от оси
у и получим график
функции
y
= kf(x)
При k ˃ 1 –
растяжение графика от оси абсцисс в k раз,
при 0 < k<
1 – сжатие графика к оси абсцисс в k раз.
ПРИМЕР:
Построить график функции
у =
3√͞͞͞͞͞х.
Построим график функции у =
√͞͞͞͞͞х .
Выполним
растяжение графика функции в три раза относительно оси х и получим
график функции
у =
3√͞͞͞͞͞х.
ПРИМЕР:
Построить график функции
у =
1/3 х3.
Построим график функции у =
х3. Выполним
сжатие графика функции у = х3 в три раза к оси х и получим
график функции
у =
1/3 х3.
Преобразования
графика с модулем.
у = |f(x)|
При f(x)
˃ 0 – график остаётся без изменений,
при f(x) <
0 – график симметрично отражается
относительно оси абсцисс.
ПРИМЕР:
Построить график функции
у =
|х2 – 6|
Построим график функции у = х2. Параллельно переносимо график вниз на 6 единиц
вдоль оси у и получим график функции
у =
х2 – 6.
Отобразим симметрично относительно оси х ту
часть графика, которая находится под осью, и получим график функции
у =
|х2 – 6|
ПРИМЕР:
Построить график функции
у =
|х3|
Отобразим симметрично относительно оси х ту
часть графика, которая находится под осью, и получим график функции
у =
|х3|
у =f(|x|)
При x ≥ 0 – график остаётся без изменений,
при x < 0 – график симметрично отражается относительно оси ординат.
ПРИМЕР:
Построить график функции
у =
(|x| – 1)2.
Построим график функции у =
х2 и
параллельно перенесём его вправо на 1 единицы вдоль оси х и получим график
функции
у =
(х – 1)2.
Оставляем ту часть графика, которая соответствует
неотрицательным значением х. Симметрично
отображаем относительно оси у часть полученного графика для неотрицательных
х и получаем график
функции
у
= (|x|
– 1)2.
ПРИМЕР:
Построить график функции
у =
5|x| – 3.
Построим график функции у =
5х и
параллельно перенесём его вниз на 3 единицы вдоль оси у и
получим график функции
у =
5x – 3.
Оставим ту часть графика, которая соответствует
неотрицательным значениям х.
Симметрично отобразим относительно оси у часть полученного графика для неотрицательных х и получим
график функции
у =
5|x| – 3.
Источник
Если к АРГУМЕНТУ функции добавляется константа, то происходит сдвиг (параллельный перенос) графика вдоль оси . Рассмотрим функцию и положительное число :
Правила:
1) чтобы построить график функции , нужно график сдвинуть ВДОЛЬ оси на единиц влево;
2) чтобы построить график функции , нужно график сдвинуть ВДОЛЬ оси на единиц вправо.
Пример 6
Построить график функции
Берём параболу и сдвигаем её вдоль оси абсцисс на 1 единицу вправо:
«Опознавательным маячком» служит значение , именно здесь находится вершина параболы .
Теперь, думаю, ни у кого не возникнет трудностей с построением графика (демонстрационный пример начала урока) – кубическую параболу нужно сдвинуть на 2 единицы влево.
Вот ещё один характерный случай:
Пример 7
Построить график функции
Гиперболу (чёрный цвет) сдвинем вдоль оси на 2 единицы влево:
Перемещение гиперболы «выдаёт» значение, которое не входит в область определения функции. В данном примере , и уравнение прямой задаёт вертикальную асимптоту (красный пунктир) графика функции (красная сплошная линия). Таким образом, при параллельном переносе асимптота графика тоже сдвигается (что очевидно).
Вернёмся к тригонометрическим функциям:
Пример 8
Построить график функции
График синуса (чёрный цвет) сдвинем вдоль оси вдоль оси на влево:
Внимательно присмотримся к полученному красному графику …. Это в точности график косинуса ! По сути, мы получили геометрическую иллюстрацию формулы приведения , и перед вами, пожалуй, самая «знаменитая» формула, связывающая данные тригонометрические функции. График функции получается путём сдвига синусоиды вдоль оси на единиц влево (о чём уже говорилось на уроке Графики и свойства элементарных функций). Аналогично можно убедиться в справедливости любой другой формулы приведения.
Рассмотрим композиционное правило, когда аргумент представляет собой линейную функцию: , при этом параметр «ка» не равен нулю или единице, параметр «бэ» – не равеннулю. Как построить график такой функции? Из школьного курса мы знаем, что, что умножение имеет приоритет перед сложением, поэтому, казалось бы, сначала график сжимаем/растягиваем/отображаем в зависимости от значения , а потом сдвигаем на единиц. Но здесь есть подводный камень, и корректный алгоритм таков:
Аргумент функции необходимо представить в виде и последовательно выполнить следующие преобразования:
1) График функции сжимаем (или растягиваем) к оси (от оси) ординат: (если , то график дополнительно следует отобразить симметрично относительно оси ).
2) График полученной функции сдвигаем влево (или вправо) вдоль оси абсцисс на (!!!) единиц, в результате чего будет построен искомый график .
Пример 9
Построить график функции
Представим функцию в виде и выполним следующие преобразования: синусоиду (чёрный цвет):
1) сожмём к оси в два раза: (синий цвет);
2) сдвинем вдоль оси на(!!!) влево: (красный цвет):
Пример вроде бы несложный, а пролететь с параллельным переносом легче лёгкого. График сдвигается на , а вовсе не на .
Продолжаем расправляться с функциями начала урока:
Пример 10
Построить график функции
Представим функцию в виде . В данном случае: Построение проведём в три шага. График натурального логарифма :
1) сожмём к оси в 2 раза: ;
2) отобразим симметрично относительно оси : ;
3) сдвинем вдоль оси на(!!!) вправо: :
Для самоконтроля в итоговую функцию можно подставить пару значений «икс», например, и свериться с полученным графиком.
В рассмотренных параграфах события происходили «горизонтально» – гармонь играет, ноги пляшут влево/вправо. Но похожие преобразования происходят и в «вертикальном» направлении – вдоль оси . Принципиальное отличие состоит в том, что связаны они не с АРГУМЕНТОМ, а с САМОЙ ФУНКЦИЕЙ.
Растяжение (сжатие) графика ВДОЛЬ оси ординат.
Симметричное отображение графика относительно оси абсцисс
Структура второй части статьи будет очень похожа.
1) Если ФУНКЦИЯ умножается на число , то происходитрастяжение её графика вдоль оси ординат.
Правило: чтобы построить график функции , где , нужно график функции растянуть вдоль оси в раз.
2) Если ФУНКЦИЯ умножается на число , то происходит сжатие её графика вдоль оси ординат.
Правило: чтобы построить график функции , где , нужно график функции сжать вдоль оси в раз.
Догадайтесь, какую функцию я буду снова пытать =)
Пример 11
Построить графики функций .
Берём синусоиду за макушку/пятки:
И вытягиваем её вдоль оси в 2 раза:
Период функции не изменился и составляет , а вот значения (все, кроме нулевых) увеличились по модулю в два раза, что логично – ведь функция умножается на 2, и область её значений удваивается: .
Теперь сожмём синусоиду вдоль оси в 2 раза:
Аналогично, период не изменился, но область значений функции «сплющилась» в два раза: .
Нет, у меня нет какого-то пристрастного отношения к синусоиде, просто я хотел продемонстрировать, чем отличаются графики функций (Примеры №№1,3) от только что построенных собратьев . Постарайтесь ещё раз проанализировать и качественнее понять эти элементарные случаи. Даже минимальные знания о преобразованиях графиков окажут вам неоценимую помощь в ходе решения других задач высшей математики!
И, конечно же, классический пример растяжения/сжатия параболы:
Пример 12
Построить графики функций .
Возьмём рога молодого оленя и вытянем их вверх вдоль оси в два раза: . Затем сожмём вдоль оси ординат в 2 раза:
И снова заметьте, что значения функции увеличиваются в 2 раза, а значения уменьшаются во столько же раз (исключение составляет точка ).
Отпустим в тундру удивлённое животное и продолжим изучать умножение функции на число: . Случаи не представляют интереса, поэтому рассмотрим отрицательные коэффициенты. Сначала распространённый частный случай :
Если ФУНКЦИЯ меняет знакна противоположный, то её график отображается симметрично относительно оси абсцисс.
Правило: чтобы построить график функции , нужно график отобразить симметрично относительно оси .
Пример 13
Построить график функции
Отобразим синусоиду симметрично относительно оси :
Ещё более наглядно симметрия просматривается у следующей типовой функции:
Пример 14
Построить график функции
График функции получается путём симметричного отображения графика относительно оси абсцисс:
Функции задают две ветви параболы, которая «лежит на боку». Обратная функция задаёт параболу целиком. С подобными графиками часто приходится иметь дело при нахождении площадей фигур, построении областей интегрирования двойных интегралов и в некоторых других задачах.
При умножении функции на отрицательное число , , построение графика следует выполнить в два этапа: сжатие (или растяжение) вдоль оси ординат, а потом – симметричное отображение относительно оси абсцисс. Конкретные примеры увидим в следующем топике.
Источник