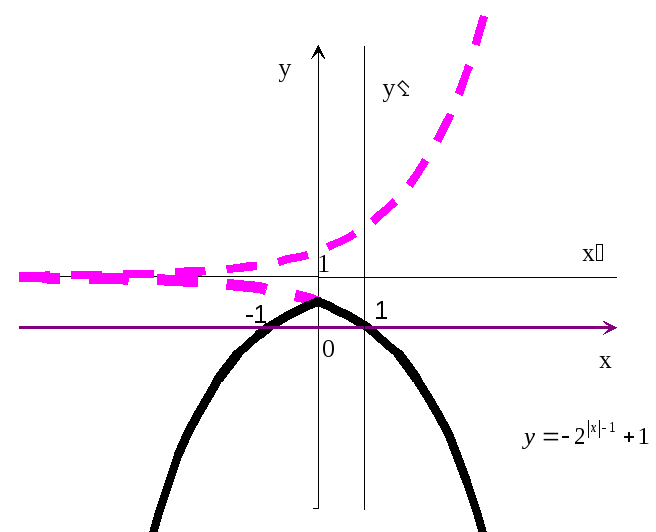
Растяжение графика функции от оси ординат
Список функций, изученных в 7 и 8 классе
Функция | Формула | График | Раздел справочника |
Прямая пропорциональность | y = kx | Прямая | 7 кл., §37 |
Линейная функция | y = kx+b | Прямая | 7 кл., §38-39 |
Обратная пропорциональность | $ y = frac{k}{x} $ | Гипербола | 8 кл., §6 |
Квадрат числа | $ y=x^2$ | Парабола | 8 кл., §18 |
Квадратный трёхчлен | $ y = ax^2+bc+c$ | Парабола | 8 кл., §28-29 |
Квадратный корень | $ y = sqrt{x}$ | Парабола | 8 кл., §22 |
Растяжение и сжатие графика по оси OX
Сравним графики пар функций, которые в общем виде можно записать так:
$$ y_1 = f(x), y_2 = f(px) $$
где $p gt 1$, произвольный положительный множитель.
Пусть p = 2.
Парабола: $y_1 = f(x) = x^2$ $ y_2 = f(2x) = (2x)^2 = 4x^2 $ $y_2 = y_1 при x_2 = frac{1}{2} x_1$ График сжимается в 2 раза по оси OX |  |
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = f(2x) = frac{4}{(2x)} = frac{2}{x}$ $ y_2 = y_1 при x_2 = frac{1}{2} x_1 $ График сжимается в 2 раза по оси OX |
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = f(2x) = sqrt{2x}$ $y_2=y_1 при x_2 = frac{1}{2} x_1$ График сжимается в 2 раза по оси OX |
|
Теперь сравним пары функций с делением на p:
$$ y_1 = f(x), quad y_2 = f left( frac{x}{p} right), quad p gt 1 $$
Пусть p = 2
Парабола: $y_1 = f(x) = x^2$ $ y_2 = f left(frac{x}{2}right) = left(frac{x}{2}right)^2 = frac{x^2}{4} $ $y_2 = y_1 при x_2 = 2x_1$ График растягивается в 2 раза по оси OX |  |
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = f left(frac{x}{2}right) = frac{4}{x/2} = frac{8}{x}$ $ y_2 = y_1 при x_2 = 2x_1$ График растягивается в 2 раза по оси OX |
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = f left(frac{x}{2}right) = sqrt{frac{x}{2}}$ $y_2=y_1 при x_2 = 2x_1$ График растягивается в 2 раза по оси OX |
|
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = f(px), quad p gt 1 $$
график второй функции сжимается в p раз по оси OX по сравнению с графиком первой функции.
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = f Biggl(frac{x}{p}Biggr), quad p gt 1 $$
график второй функции растягивается в p раз по оси OX по сравнению с графиком первой функции.
Заметим, что данные утверждения справедливы не только для рассмотренных функций, но и для любых других (синусов, косинусов, логарифмов и т.п.)
Растяжение и сжатие графика по оси OY
Сравним графики пар функций, которые в общем виде можно записать так:
$$ y_1 = f(x), quad y_2 = Af(x) $$
где $A gt 1$, произвольный положительный множитель.
Пусть A = 2.
Парабола: $y_1 = f(x) = x^2$ $ y_2 = 2f(x) = 2x^2 $ $y_2 = 2y_1 при x_2 = x_1$ График растягивается в 2 раза по оси OY |  |
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = 2f(x) = frac{8}{x}$ $ y_2 = 2y_1 при x_2 = x_1$ График растягивается в 2 раза по оси OY |
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = 2f(x) = 2sqrt{x}$ $y_2 = 2y_1 при x_2 = x_1$ График растягивается в 2 раза по оси OY |
|
Теперь сравним пары функций с делением на A:
$$ y_1 = f(x), quad y_2 = frac{1}{A} f(x), quad A gt 1 $$
Пусть A = 2
Парабола: $y_1 = f(x) = x^2$ $ y_2 = frac{1}{2}f(x) = frac{x^2}{2}$ $y_2 = frac{1}{2}y_1 при x_2 = x_1$ График сжимается в 2 раза по оси OY |  |
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = frac{1}{2}f(x) = frac{2}{x}$ $ y_2 = frac{1}{2}y_1 при x_2 = x_1$ График сжимается в 2 раза по оси OY |
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = frac{1}{2}f(x) = frac{sqrt{x}}{2}$ $y_2 = frac{1}{2}y_1 при x_2 = x_1$ График сжимается в 2 раза по оси OY |
|
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = Af(x), quad A gt 1 $$
график второй функции растягивается в A раз по оси OY по сравнению с графиком первой функции.
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = frac{1}{A} f(x), quad A gt 1 $$
график второй функции сжимается в A раз по оси OY по сравнению с графиком первой функции.
Заметим, что данные утверждения справедливы не только для рассмотренных функций, но и для любых других (синусов, косинусов, логарифмов и т.п.)
Примеры
Пример 1. Постройте в одной координатной плоскости графики функций:
$$ y = sqrt{x}, y = sqrt{3x}, y = sqrt{frac{x}{3}}, y = 3sqrt{x} $$
Сделайте выводы.
По сравнению с графиком $y = sqrt{x}$:
- график функции $y = sqrt{3x}$ сжимается в 3 раза по оси OX(←)
- график функции $y = sqrt{frac{x}{3}}$ растягивается в 3 раза по оси OX(→)
- график функции $y = 3sqrt{x}$ растягивается в 3 раза по оси OY(↑)
Пример 2*. Постройте в одной координатной плоскости графики функций:
$$ y = f(x), y = f(2x), y = f Biggl(frac{x}{2}Biggr), y = 2f(x) $$
где $f(x) = x^2+3x+2$
Сделайте выводы.
Исходная функция $y = f(x) = x^2+3x+2$
Остальные функции
$$ y = f(2x) = (2x)^2+3 cdot (2x)+2 = 4x^2+6x+2 $$
$$ y = fBiggl(frac{x}{2}Biggr) = Biggl(frac{x}{2}Biggr)^2+3 cdot Biggl(frac{x}{2}Biggr) +2 = frac{x^2}{4}+ frac{3}{2} x+2 $$
$$ y = 2f(x) = 2x^2+6x+4 $$
Получаем:
По сравнению с графиком $y = f(x) = x^2+3x+2$:
- график функции y = f(2x) сжимается в 2 раза по оси OX(→)
- график функции $y = f left(frac{x}{2}right)$ растягивается в 2 раза по оси OX(←)
- график функции y = 2f(x) растягивается в 2 раза по оси OY(↑)
Рейтинг пользователей
80
Ilay_YouTube
70
Георгий Федозов
60
Настя Вяземская
50
fubers
50
taty20
Источник
ЦЕЛИ: 1) рассмотреть графики функций y=f(x), y=kf(x),
y=f(x)+n, y=f(x-m) и y=f(x-m)+n и их свойства, используя ПК и
программу Advanced Grapher;
2)расширить представления о преобразованиях
графиков более сложных функций;
3)способствовать развитию у учащихся навыков
чтения графиков и построения графиков функций.
I. Новый материал – объяснительная лекция.
Графики функций широко используются в
различных областях инженерных знаний, поэтому
умение строить, “читать”, прогнозировать их
“поведение” имеют огромную роль в практической
деятельности инженерных работников, гидро,
метеорологов и людей других “математических”
специальностей.
Выясним, какая связь существует между
графиками функций y = f(x) и y = kf(x), где k-число, не
равное нулю.
Пусть графиком функции y = f(x), область
определения которой- промежуток[-2;4],является
кривая, изображённая на рис.1а f(x) =
x(x-3)(x+1).
Рассмотрим сначала случай, когда k>1.Построим
график функции y = kf(x), где k=2. Для этого расстояние
каждой точки графика функций y = f(x) от оси X
увеличим в 2раза, т.е.умножим её ординату на 2.
Построение выполним с помощью программы Advanced
Grapher, набрав формулу функции F1 с клавиатуры.
Заметим, что точки с абсциссами 0; 3; -1,
принадлежащие оси Х, останутся на месте, т.к.их
ординаты равны нулю (0*2х = 0).Все остальные точки
графиков у1, и у, имеющие одинаковые
абсциссы, будут лежать соответственно на
перпендикулярах к оси Х, причём каждая точка
графика функции у= 2f(x)
будет находиться от оси Х на расстоянии в 2 раза
большем, чем соответственная точка графика
функции y = f(x). (рис. 1б).
Рассмотрим теперь случай, когда О < k < 1,
например k =, и
построим график функции y= kf (x), при k = , используя программу Advanced Grapher.
Опять же заметим, что точки с абсциссами -1; 0 и 3,
принадлежащие оси Х, останутся на месте ( 0* = 0 ), а каждая точка
графика функции y= f (x), будет
находиться от оси Х на расстоянии в 2 раза
меньшем, чем соответственная точка графика
функции y = f(x) (рис.1в).
Делаем вывод о том, что график функции y = f(x) при k
< 1 можно получить из графика функции y = f(x)
растяжением от оси Х исходного графика в k раз, а
при О < k < 1- сжатием к оси Х графика функции y =
f(x) в раз.
И рассмотрим случай, когда k< 0. Ограничимся
значением k = -1, т.е. выясним, как можно построить
график функции y= -f(x),
зная график функции y = f(x).
Задав с клавиатуры формулу графика y = -f(x) и
получив соответствующее изображение на экране (рис. 1г), заметим, что каждой точке
графика y, кроме точек с
абсциссами -1; 0 и 3, соответствует точка графика y =
f(x) с противоположной ординатой.
Соответственно делаем вывод, что график
функции y = -f(x) можно получить с помощью симметрии
относительно оси Х.
Аналогично, графики функций y = kf(x) и y = -kf(x) при
любом k0 симметричны
относительно оси Х.
Иначе говоря, чтобы построить график функции y =
kf(x), где k < 0, можно сначала построить график
функции y = -kf(x), где -k > 0, а затем отобразить его
симметрично относительно оси Х.
Выясним, как связаны между собой графики
функций y = f(x) и y = f(x)+n, где n –произвольное число.
Рассмотрим графики функций y = x, y = x — 4 , y= x-4, y = x+ , y= x- (рис. 2).
Рассматривать будем попарно графики функций у
и у(рис.2а),
у и y(рис.2б),
у и y(рис.2в),
у и y(рис.2г).
Моментальное построение графика каждой из выше
указанных функций даст возможность сделать
вывод, что график функции y = f(x) + n можно получить
из графика функции y = f(x) с помощью сдвига вдоль
оси Y на n единиц вверх, если n>0, или на единиц вниз, если
n<0.
Выясним теперь, как связаны между собой графики
функций y = f(x) и y = f(x-m), где m – произвольное число.
Рассмотрим графики функций y = (x-3), y = (x+2), y = (x), y = (x+).
Получаем рис.3 и делаем вывод, что
график функции y = f(x) можно получить с помощью
сдвига вдоль оси Х на m единиц вправо, если m>0,
или на единиц
влево, если m<0.
Из курса алгебры VII класса известно, что график
функции y = x (парабола)
симметричен относительно ось У. Точку
пересечения параболы с осью симметрии называют
вершиной параболы.
Построим, используя программу Advanced Grapher, в одной
системе координат графики функций y = x, у== x+2, y= (х-3) и y= (х-3) +2 ( рис.4).
Учащимся наглядно видно, что у параболы у== x+2 осью симметрии является ось У, а у
параболы y= (х-3) — прямая х = 3. Графиком же
функции y= (х-3) +2 является парабола с
вершиной в точке (3;2) и осью симметрии её является
прямая х = 3.
Из наглядного наблюдения учащиеся видят, что
при построении графика функции у = (х-3) +2 нужно последовательно
выполнить два параллельных переноса: один в
направлении оси У на 2 единицы вверх, а другой в
направлении оси Х на 3 единицы вправо.
Делаем вывод, что графиком функции вида у = (х-m) +n является парабола с
вершиной в точке А(m;n) .А также обобщаем выше
рассмотренные преобразования графиков и делаем
вывод, что график функции y = f(x-m)+n может быть
получен из графика функции y=f(x) в результате
последовательно выполненных двух параллельных
переносов: сдвига вдоль оси Х на m единиц и сдвига
графика функции у = (х-m)
вдоль оси У на n единиц.
II. Закрепление
.
У: Изобразите на координатной плоскости
заданные точки и определите, используя обороты
“выше на…” и “ниже…”, взаимное расположение
соответствующих точек:
а) А(-1;7) и А1(-1;10) б) В(2;7) и В1(2;5) в) С (0;-6)
и С1(0;-5) г) Д (3;-4) и Д1(3;-7) .
У: Как найти расстояние между точками, имеющими
одинаковые ординаты? Закончите предложение:
“Если точки имеют одинаковые ординаты, то
расстояние между ними равно…”
Обучающая исследовательская работа.
(карточки-распечатки см. Приложение 1)
I вариант.
1. Заданы функции y = f(x) и y = f(x) + 2. заполните таблицу значений этих
функций и сделайте вывод о взаимном расположении
точек данных функций и их графиков:
| 1 | 2 | 4 | 6 | 7 |
y=f(x) | 5 | 7 | -5 | ||
y=f(x)+2 | 3 | -11 |
Д: Любая точка графика y = f(x)+2 с абсциссой X находится на 2 единицы
“выше”, чем точка графика y = f(x) с той же самой
абсциссой; а график функции y = f(x)+2 можно получить из графика y = f(x)
параллельным переносом вдоль оси ординат на 2
единицы “вверх”.
II вариант.
1. Заданы функции y = f(x) и y = f(x) – 3. заполните
таблицу значений этих функций и сделайте вывод о
взаимном расположении точек данных функций и их
графиков:
| 1 | 3 | 5 | 9 | |
y=f(x) | 4 | -6 | 5 | ||
y=f(x)-3 | -3 |
Д: Любая точка графика y = f(x)-3 с абсциссой X находится на 3 единицы
“ниже”, чем точка графика y = f(x) с той же самой
абсциссой; а график функции y=f(x)-3 можно получить из графика y = f(x)
параллельным переносом вдоль оси ординат на 3
единицы “вниз”.
У: С помощью какого преобразования можно
получить график функции y = f(x)+a, а0 из графика функции y = f(x).
Д: Обобщённый вывод (записать в тетрадь): График
функции y1= f(x)+a, а0 можно получить из графика функции y = f(x)
параллельным переносом вдоль оси ординат на единиц “вниз”,
если а<0, и на
единиц “вверх”, если а>0.
У: Пусть даны графики функций y = f(x) и y = f(x)+7. Известно, что один из
них проходит через начало координат. Определите
точку пересечения другого графика с осью
ординат.
Д: A (0;7) или А (0;-7).
У: Пусть даны графики функций y = f(x) и y = f(x)+c. Известно, что один из
них проходит через точку А(-11;231) и другой через
точку А (-11;132). Найдите
все возможные значения С.
Д: 99 или -99.
I вариант.
2. Постройте графики функций, используя
известный график y = kx:
a) y = x-4 ; б) у = x+1;
в) у = 2 x-1.
3.
II вариант.
2. Постройте графики функций, используя
известный график y = kx:
а) у = -x+3; б) у = -0,5x+2; в) у = -2x-3.
3.
У: Изобразите на координатной плоскости
заданные точки и определите, используя обороты
“левее на …” и “правее на …” взаимное
расположение следующих точек:
а) А (-1;7) и А (6;7) б) С (8;-6)
и С (14;-6) в) В (2;3) и В (-2;3) г) Д (-13;_4) и Д (-3;-4).
У: Как найти расстояние между точками, имеющими
одинаковые абсциссы? Закончите предложение:
“Если точки имеют одинаковые абсциссы, то
расстояние между ними равно…”
I, II вариант.
4. Заданы функции y=f(x), y=
f(x+2) и y= f(x-3). Заполните
таблицу значений этих функций:
У: Как взаимно расположены точки графиков
функций y = f(x) и y = f(x+2)?
Каким образом можно получить график функции y= f(x+2) из графика функции y =
f(x)?
Д: Любая точка графика y=
f(x+2) с абсциссой х-2
находится на 2 единицы “левее”, чем точка
графика y=f(x) с абсциссой х, а график функции y= f(x+2) можно получить из графика y = f(x),
“сдвинув” его на 2 единицы влево вдоль оси
абсцисс.
У: Как взаимно расположены точки графиков
функций y = f(x) и y= f(x-3)?
Каким образом можно получить график функции y= f(x-3) из графика функции y =
f(x)?
Д: Любая точка графика y= f(x-3) с абсциссой х+3
находится на 3 единицы “правее”, чем точка
графика y = f(x) с абсциссой х, а график функции y= f(x-3) можно получить из графика функции y =
f(x) “сдвинув” его на 3 единицы вправо вдоль оси
абсцисс.
У: Попытайтесь сделать вывод о том как можно
получить график функции y= f(x+а) из графика функции y = f(x)?
Д: График функции y=
f(x+а) можно получить из графика функции y = f(x),
“сдвинув” его на единиц вправо вдоль оси абсцисс, если
а<0, и на
единиц влево вдоль оси абсцисс, если а>0.
У: Пусть даны графики функций y = f(x) и y= f(x+7). Известно, что один из
них проходит через начало координат. Какую точку
пересечения графика с осью абсцисс можно указать
наверняка?
Д: А(-7;0) и А (7;0).
У: Опишите как расположены относительно друг
друга графики функций (задания 5-9 выполнены на
карточках-распечатках, ответы в устной форме):
5. y = f(x-2) и y = f(x+7).
6. y = f(2x) и y = f(2x-4).
7. y = f(2x) и y = f(2x+1).
8. y = f(0,5x) и y = f(0,5x-4).
9. y = f() и . y = f(-1).
III . Лабораторно-исследовательская работа.
(все задания выполнены на
карточках-распечатках, ответы см. в приложении
2)
I вариант.
10. Постройте графики функций, используя
программу Advanced Grapher :
а) у = (x-4). б) у = (x+2).
11. Пусть дан график функции y=f(x). Как получить
график функции y = f(x+3)-4?
12. Постройте графики функций, используя
программу Advanced Grapher:
а) у = -4; б) у =
(x+3)-4.
II вариант.
10. Постройте графики функций, используя
программу Advanced Grapher :
а) у = 2(x-1), б) у = -(x+3).
11. Пусть дан график функции y=f(x). Как получить
график функции y = f(x-5)+2?
12. Постройте графики функций, используя
программу Advanced Grapher:
а) у =+2; б) у =(x-5)+2.
III вариант.
10. Постройте графики функций, используя
программу Advanced Grapher :
а) у = -0,5(x-4); б) у = (2x-3).
11. Пусть дан график функции y = f(x). Как получить
график функции y = f(x+1)+3?
12. Постройте графики функций, используя
программу Advanced Grapher:
а) у =+3; б) у =
(x+1)+3.
IV вариант.
10. Постройте графики функций, используя
программу Advanced Grapher :
а) у = 4x+4х+1; б) у = —х-1.
11. Пусть дан график функции y=f(x). Как получить
график функции y = f(x-2)-1?
12. Постройте графики функций, используя
программу Advanced Grapher:
а) у =-1; б) у =
(x-2)-1.
Источник
3.1 Сжатие (растяжение) графика вдоль оси ординат
Рассмотрим
функцию вида y=A
,
где A>0.
Нетрудно заметить, что при равных
значениях аргумента ординаты графика
этой функции будут в A
раз больше ординат графика функции
y=f(x)
при A>1
или в
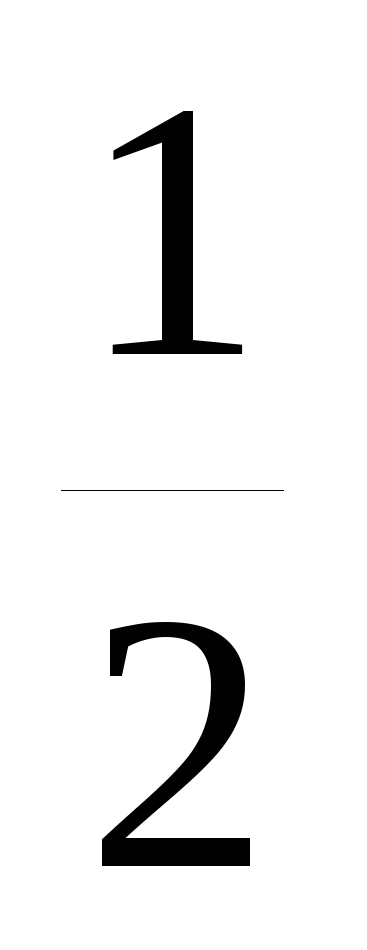
раз меньше ординат графика функцииy=f(x)
при A<1.
Таким образом, получаем следующее
правило.
Для
построения графика функции y=A
следует построить график функции y=f(x)
и увеличить его ординаты в A
раз при A>1
(произвести растяжение графика вдоль
оси ординат) или уменьшить его ординаты
в
раз приA<1
(произвести сжатие графика вдоль оси
ординат). Полученный график является
графиком функции y=A
.
Пример
13. Построить
график функции y=2cos
x.
Р
е ш е н и е: Строим график функции y=cos
x
(рис.16 – пунктирная кривая) и растяжением
этого графика вдоль оси ординат в 2
раза получаем график функции y=2cos
x
(сплошная кривая).
Пример
14. Построить
график функции y=
x2.
Р
е ш е н и е: Строим график функции y=x2
и сжатием этого графика в 3 раза вдоль
оси ординат получаем график функции
y=
x2
(рис.17).
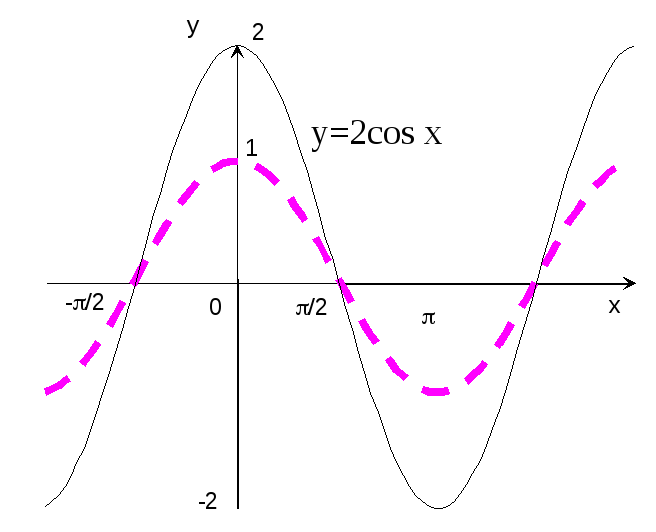
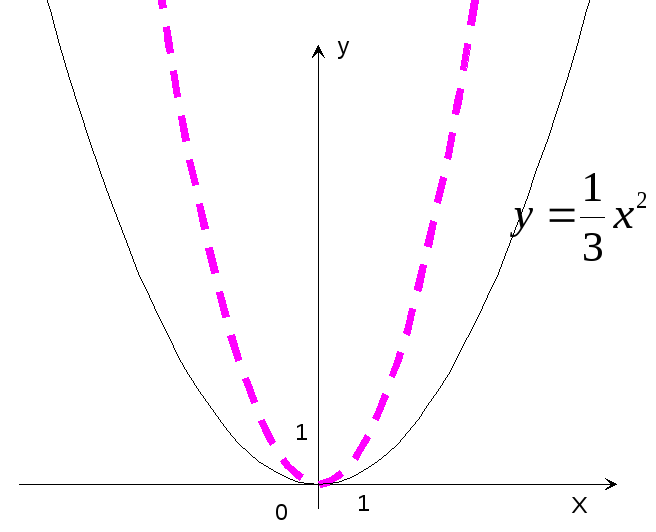
Рис.16
Рис.17
3.2. Сжатие (растяжение) графика вдоль оси абсцисс
Пусть
требуется построить график функции
y=f(x),
где >0.
Рассмотрим функцию y=f(x),
которая в произвольной точке x=x1
принимает значение y1=f(x1).
Очевидно,
что функция y=f(x)
принимает такое же значение в точке
x=x2,
координата
к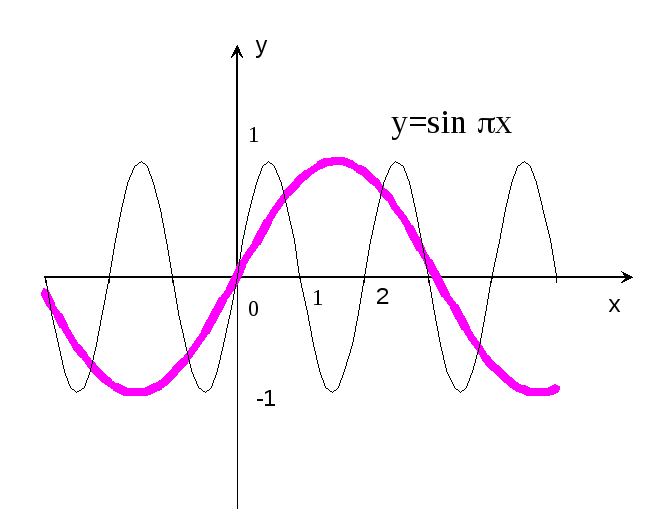
оторой
определяется равенствомx1=x2,
или x2=
,
причём это равенство справедливо для
совокупности всех значений x
из области определения функции.
Следовательно, график функции y=f(x)
оказывается сжатым (при >1)
или растянутым (при <1)
вдоль оси абсцисс относительно графика
функции y=f(x).
Таким образом, получаем следующее
правило.
Для
построения графика функции y=f(x)
следует построить график функции y=f(x)
и уменьшить его абсциссы в
раз при >1
(произвести сжатие графика вдоль оси
абсцисс) или увеличить его абсциссы в
раз при<1
(произвести растяжение графика вдоль
оси абсцисс). Полученный график является
графиком функции y=f(x).
П
Рис. 18
ример 15.Построить
график функции
x.
Р
е ш е н и е: Строим график функции
x
(рис.18 – пунктирная кривая), и проводя
его сжатие в
раз вдоль оси абсцисс, получаем график
функции
x
(сплошная кривая). Период этой функции
уже равен не 2,
а
=2.
График пересекает ось абсцисс в точкахx=0,
…
.
Пример
16. Построить
график функции
.
Р
е ш е н и е: Строим график функции
и, растянув его вдоль оси абсцисс в 3
раза, получаем график функции
.
4. Комбинация переноса, отражения и деформации
Рис.
19
Очень часто при построении графиков
функций применяют композицию приёмов,
изложенных в пунктах 1-3. Последовательное
применение ряда таких приёмов позволяет
существенно упростить построение
графика исходной функции и нередко
свести его в конце концов к построению
одной из простейших элементарных
функций.
Рассмотрим,
как с учётом изложенного следует,
например, построить
график функции вида y=Af(x+a)+b.
Запишем
исходную функцию в виде y=Af
[
( x+
) ] +b
и схему поэтапного её упрощения
(последовательность преобразований):
1
.y=Af
[
( x+
) ] + b
; перенос оси абсцисс на b
единиц;
2
.y=Af
[
( x+
) ]; перенос оси ординат на
единиц;
3. y=Af
[
x
]; отражение графика относительно оси
абсцисс
(
этап
выполняется только приA<0);
4
.y=A·
f
(x); сжатие
или растяжение графика
вдоль оси ординат;
5. y=f
(x) отражение
графика относительно оси ординат
(
этап
выполняется только при<0);
6
.y=f
(
x); сжатие
или растяжение вдоль оси абсцисс;
7. y=f
( x);
Проводя
построение графика шаг за шагом в
порядке, обратном порядку упрощения
вида функции с учётом всех указанных
правил, получим график исходной функции.
Пример 17. Построить
график функции y=
.
Р
е ш е н и е: Схема построения графика :
y
=
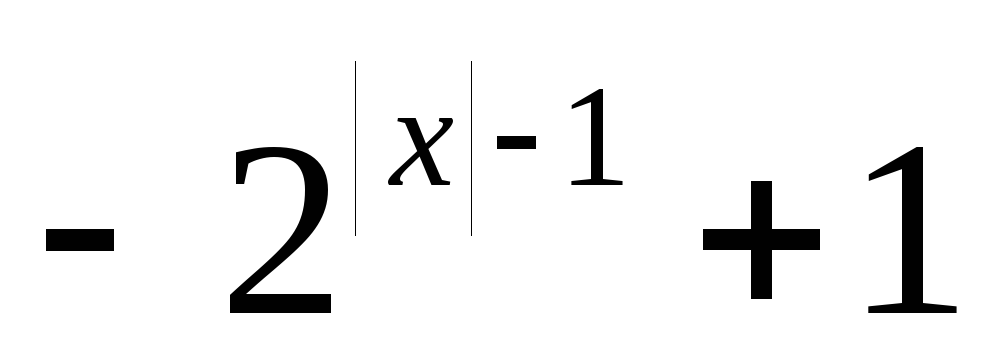
x
0,
y=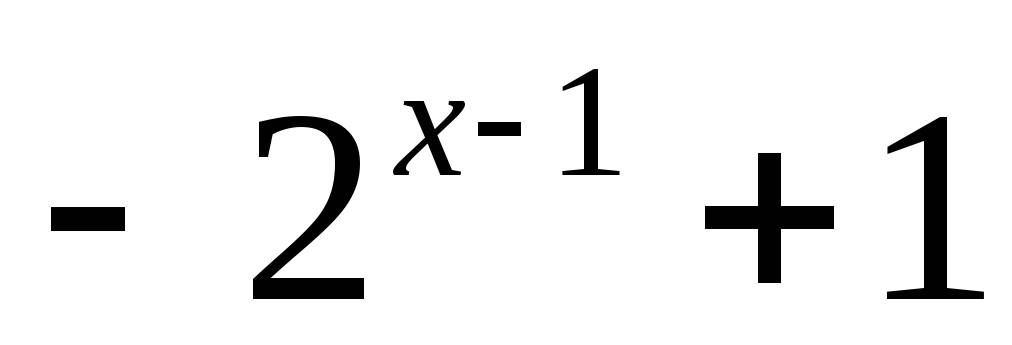
;y=
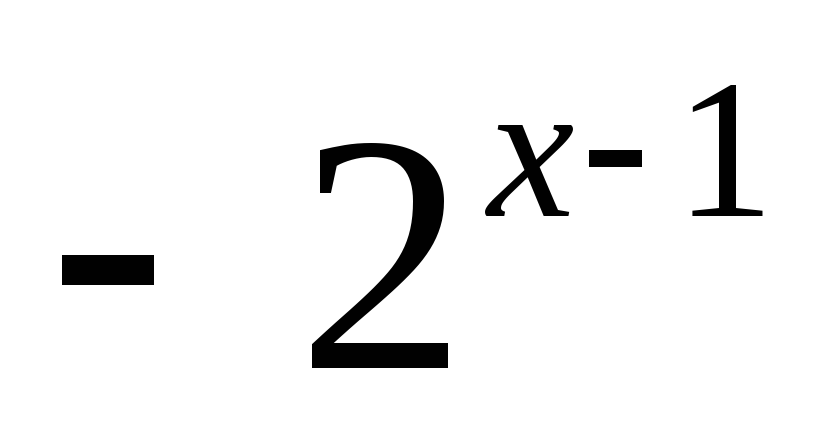;у=
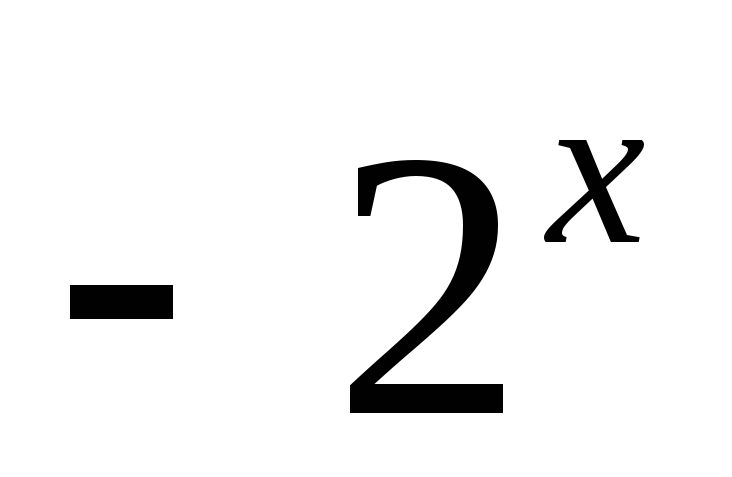;y=
;
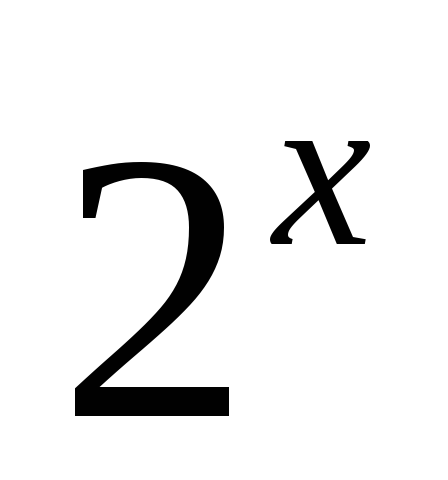Итак,
построение графика исходной функции
следует начинать с построения графика
функции y=
.
График (рис.20) пересекает ось ординат
в точке
(из условияx=0),
а ось абсцисс в точках x=1
(из условия y=0,
т.е.
=0).
В
заключении отметим, что порядок упрощения
целесообразно проводить в следующей
последовательности.
Использование
чётности или нечётности функции.Перенос осей.
Отражение и
деформация.
Построение
же графика, как обычно, выполняется в
обратной последовательности.
Рис.20
Задание для
самостоятельного выполнения
Ниже
приводятся тексты заданий для
самостоятельного выполнения. Вам
необходимо построить графики функций,
оформить работу отдельно от решений по
другим предметам и выслать в адрес
Хабаровской краевой заочной
физико-математической школы.
М.11.2.1 С
помощью элементарных преобразований
постройте графики следующих функций:
y=x2-2;
y=(x+1)2;
y=sin
x;y=-
3sin x;y=tg
;
М.11.2.2.
Написать последовательность преобразований
и построить графики следующих функций:
y=
;y=(x-1)3+2;
y=ln
(1-x);y=tg(-
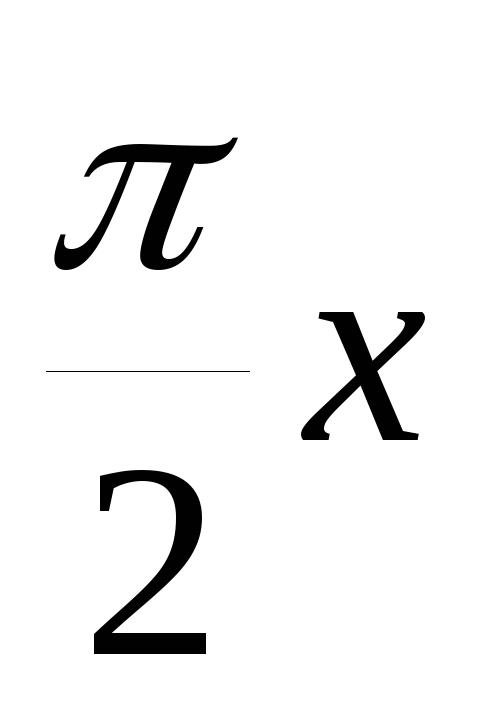);y=
cos(2x-1)-2.
Хабаровская краевая заочная
физико-математическая школа
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник