Растяжение балки эпюр сил
Построение эпюр продольных сил – это решение статически определимой задачи. Производится для выявления картины нагрузки упругого тела. Вернее, уточнения ее схематизации.
Необходимо для определения наиболее напряженного, так называемого «опасного» сечения. Затем методами сопромата (сопротивления материалов) проводится анализ с прогнозированием перемещений элементов конструкции.
Но всему свое время. Сначала немного о терминах.
Основные понятия
Брусом (балкой) называют тело, вытянутое вдоль оси. То есть длина преобладает над шириной и высотой.
Если имеются только осевые (продольные) силы, то объект подвергается растяжению/сжатию. В этом случае в материале возникают только нормальные поперечному сечению силы противодействия и тело считают стержнем.
Статическая определимость подразумевает достаточность схемы для установления внутренних усилий противодействия. Участок – часть балки с неизменным сечением и характерной нагрузкой.
Правила построения учитывают знаки усилий. Растягивающие принимают положительными, сжимающие – отрицательными.
В системе СИ силы измеряются в ньютонах (Н). Длины в метрах (м).
Что такое эпюра продольных сил
Показывает, какой силой (в нашем предположении нормальной) загружен каждый участок. По всей длине стержня. Иначе говоря, эпюра – наглядное графическое изображение изменения нагрузки по всей длине конструкции.
Как построить эпюру продольных сил
Используется метод сечений. Балка виртуально рассекается на каждом участке и ищется противодействующая N. Ведь задача статическая.
Сопротивление рассчитывается по формуле:
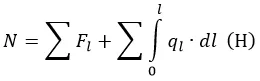
где:
Fl – действующие на участке l силы (Н);
ql – распределенные нагрузки (Н/м).
Порядок построения:
1. Рисуется схема балки и механизмов закрепления;
2. Производится разделение на участки;
3. Для каждого рассчитывается N с учетом знаков. Если у балки есть незакрепленный конец, то начинать удобнее именно с него. В противном случае считается реакция опор. И оптимальнее выбирать сечение с меньшим количеством действующих факторов:
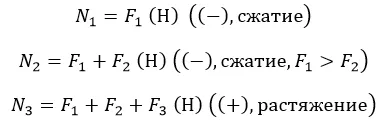
Нетрудно заметить, что последнее уравнение дает еще и реакцию опоры;
4. Параллельно оси стержня намечается база эпюры. Положительные значения масштабировано проставляются выше, отрицательные – ниже. Эпюру наглядно совмещать с расчетной схемой. Итоговый результат и промежуточные сечения показаны на рис. 1.
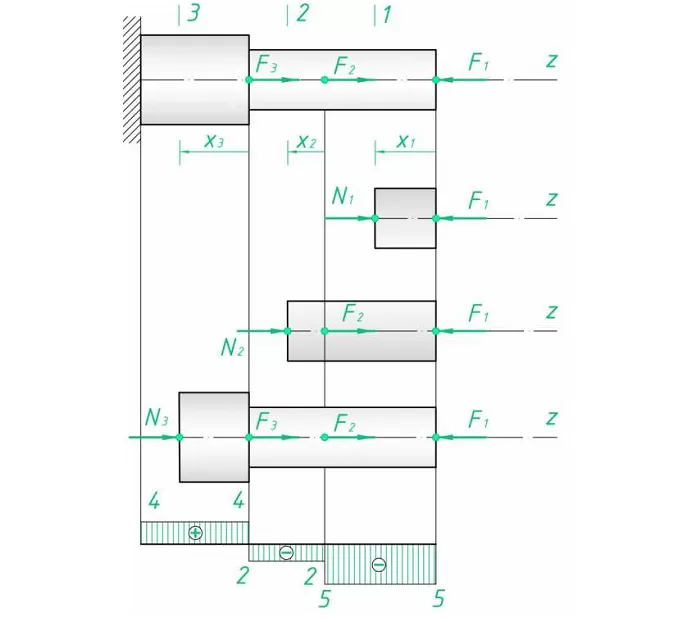
Рис. 1. Эпюра продольных сил
Рассмотрим случай:
F1 = 5 (кН);
F2 = 3 (кН);
F3 = 6 (кН).
Вычислим:
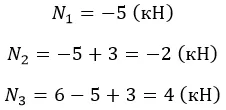
Проверить эпюру можно по скачкам: изменения происходят в точках приложения сил на их величину.
Пример построения эпюр и решения задач
Построить эпюру сил для следующего случая (рис. 2):
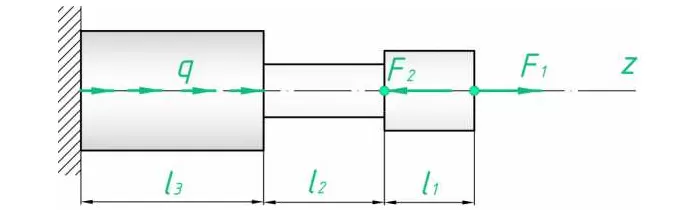
Рис. 2
Дано:
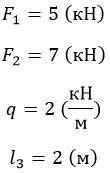
Решение.
Разбиение на участке вполне очевидно. Найдем сопротивление на выделенных:
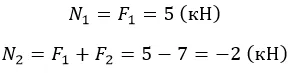
Распределенная нагрузка зависит от длины, на которой приложена. Поскольку нарастает линейно, значение N2 будет постепенно увеличиваться/уменьшаться в зависимости от знака q.
Эпюра такого вида усилия представляет собой прямоугольный треугольник с катетами l3 и ql3 (в масштабе). Поскольку распределение линейно.
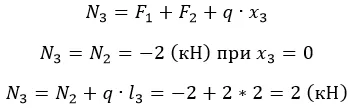
По полученным данным строим эпюру (рис. 3).
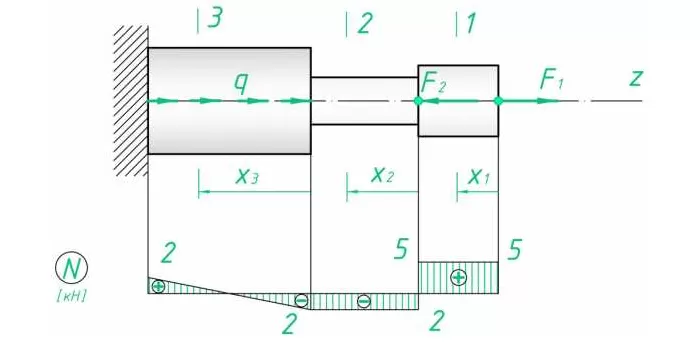
Рис. 3
Заключение
Приведенный алгоритм является предварительным этапом в расчете модели на прочность. «Слабое» место находится уже с учетом площади поперечного сечения.
В сети имеются онлайн сервисы для помощи в расчетах при вычерчивании. Но стоит ли ими пользоваться, если процедура настолько проста? Если не запутаться в знаках, конечно. Это самая распространенная ошибка.
Источник
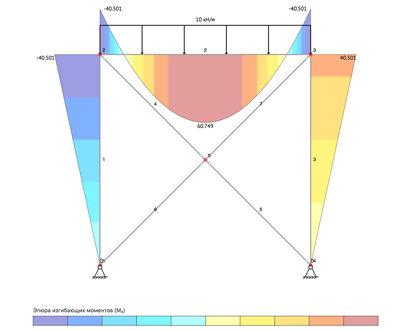
Расчет рамы/фермы
Расчет
статически-неопределимых систем
Расчет
методом конечных элементов
Построение
эпюры моментов (М)
Построение
эпюры поперечных сил (Q)
Построение
эпюры продольных сил (N)
Построение
эпюры моментов (М)
Построение
эпюры поперечных сил (Q)
Построение
эпюры продольных сил (N)
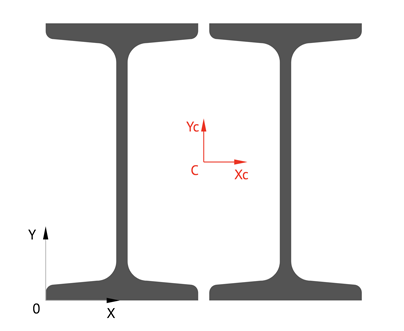
Расчет
геометрических характеристик поперечного сечения
Определение
центра тяжести, моментов инерции, моментов сопротивления
Формирование
подробного отчета
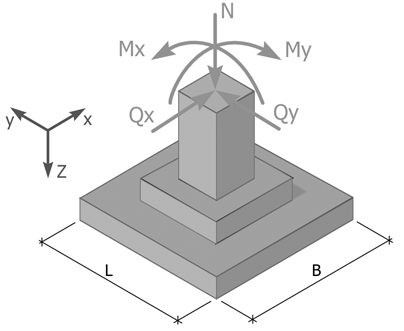
Расчет
столбчатого фундамента
Расчет
ленточного фундамента
Формирование
подробного отчета
Расчет
статически-неопределимых систем
Расчет
методом конечных элементов
Построение
эпюры моментов (М)
Построение
эпюры поперечных сил (Q)
Построение
эпюры продольных сил (N)
Источник
Очень важно уметь строить эпюры для балок, работающих на изгиб! Так как построение эпюр, является неотъемлемой частью любого прочностного расчёта и большинство элементов, из которых состоят современные инженерные сооружения, работают на изгиб. Поэтому в сопромате, очень много внимания уделяется как раз данным эпюрам: поперечных сил и изгибающих моментов. Для краткости, их ещё называют эпюрой моментов и эпюрой сил. В этой статье, рассмотрим, как рассчитать эпюры традиционным методом, а также быстрым, с помощью которого эпюры рисуются за считаные минуты. В статье, построение показано на примере консольной и опирающейся на две опоры балки. Показано, как учитывать сосредоточенные силы и моменты, а также распределённые нагрузки.
Построение эпюр для консольной балки
В качестве первого примера, возьмём балку, защемлённую с левого торца жёсткой заделкой и загруженной силой равной 5 кН и моментом равным 10 кНм. Длины участков даны на расчётной схеме. Нам предстоит рассмотреть два участка. Границами участков будут являться места приложения сил, моментов, начало и конец приложения распределённых нагрузок.
Первым делом, вводим систему координат, ось x пускаем вдоль оси балки, ось y перпендикулярно ей, а ось z будет перпендикулярна плоскости, в которой размещены две первые оси и будет направлена «к нам».
В поперечных сечениях балки под действием приложенной нагрузки будут возникать два внутренних силовых фактора: поперечная сила и изгибающий момент. Наша задача выяснить, какой величины эти факторы во всех сечениях балки. Для наглядности, результат решения фиксируют в виде так называемых эпюр.
Эпюра строится по всей длине балки, ордината эпюры, под исследуемым сечением, показывает величину внутреннего усилия в этом сечении.
Эпюра поперечных сил
Начнём знакомство с поперечными силами с правила знаков для эпюр. После чего последовательно рассчитаем и построим эпюры для первого и второго участка балки.
Правило знаков для поперечной силы
При построении эпюр поперечных сил нужно придерживаться следующих правил знаков:
- Если внешняя сила стремится повернуть балку по часовой стрелке, то поперечную силу считаем положительной. Эпюру откладываем выше нулевой линии со знаком плюс.
- Если сила поворачивает балку против часовой стрелки, то поперечная сила будет отрицательной, и на эпюре будет откладывать ниже нулевой линии.
Возможно, сейчас будет немного непонятны данные правила, но прочитав следующие 2 блока статьи, вы поймёте, как применять эти правила в действии.
Поперечные силы на первом участке
Рассмотрим первым участок равный двум метрам. Сделаем мысленно сечение на расстоянии x1 от свободного торца и запишем законы изменения эпюр на этом участке. Законы эти выражаются из уравнений равновесия статики. Статика говорит нам, что тело находится в равновесии, если выполняются следующие условия:
Если суммы проекций всех сил на обе оси равны нулю и сумма моментов относительно точки равна нулю.
Для поперечной силы возьмём сумму проекций на ось y:
Из этого уравнения выражаем поперечную силу Q = F. Так как внешняя сила стремиться повернуть балку по часовой стрелке, то поперечную силу считаем положительной. Причем видно, из полученного закона поперечной силы, что Q постоянна по всей длине участка. Откладываем на эпюре Q = F = 5 кН. Эпюру подписываем как Qy, где y значит, что направление поперечные силы совпадет с направлением этой оси.
Поперечные силы на втором участке
На втором участке, поперечная сила будет равна: Qy2 = Qy1;
Так как на этом участке, действует все та же сила F. Момент в уравнениях поперечных сил не учитывается, что является следствием уравнений статики.
Эпюра изгибающих моментов
В этом блоке статьи будем учиться строить эпюру моментов, здесь нюансов несколько больше, чем для эпюры поперечных сил. Начнём, пожалуй, с правил знаков, которые приняты для этой эпюры.
Правила знаков для изгибающих моментов
- Если внешняя сила или момент растягивают «верхние волокна» то эпюра откладывается сверху.
- Если сила или момент силы растягивают «нижние волокна», то эпюра откладывается ниже нулевой линии.
То есть, обычно, при построении эпюр изгибающий моментов знаки не указываются. Эти эпюры откладываются со стороны «растянутых волокон». Так, и удобнее читать эпюры и откладывать их.
Не всегда их откладывают так! Студентов некоторых специальностей, чаще всего машиностроительных, учат откладывать эпюры со стороны «сжатых волокон». Строители откладывают со стороны «растянутых волокон», в своих статьях я буду придерживаться этого правила, так как привык к нему.
Изгибающий момент на первом участке
Для изгибающих моментов на первом участке, запишем сумму моментов, относительно точки С, в которой ранее сделали сечение:
Отсюда получаем:
Это закон изменения изгибающих моментов по длине участка. В отличие от поперечных сил, изгибающие моменты будут меняться в пределах этого участка.
- Если подставить вместо x1 — ноль, который соответствует началу участка, то получим, что М = 0.
- Если подставим вместо x1 — 2 (конец участка), то получим:
С учётом вышеописанных правил знаков, мысленно представляем себе, что сила стремится растянуть верхние волокна, поэтому откладываем рассчитанные значения на эпюре сверху, получив эпюру в виде прямоугольного треугольника. Обязательно, подписываем эпюру как Mz, где z означает, что все изгибающие моменты поворачивают относительно этой оси.
Будет продолжение…
Источник
Пример 1.
Построить эпюры внутренних усилий Qy, Mx для балки (см. рис.).
а)
б)
Решение.
1. Определение опорных реакций
Из уравнений равновесия
находим
2. Определение Qy, Mx методом сечений (рис. б) и построение эпюр
Из уравнений равновесия отсеченных частей балки находим:
По полученным значениям строим эпюры (рис. а). Отметим, что сосредоточенный момент не повлиял на характер эпюры Qy. На эпюре моментов сосредоточенный момент вызвал скачок на величину этого момента. Наклон прямых на эпюре моментов одинаков, что соответствует правилу Журавского.
Пример 2.
Построить эпюры Qy, Mx для балки (см. рис. а).
а)
б)
Решение.
1. Определение опорных реакций
Из уравнений равновесия
Находим
2. Определение Qy, Mx методом сечения и построение эпюр
Из уравнения равновесия отсеченной части балки (рис. б) находим
Как видно, график-эпюра 
– прямая линия, а 
– квадратичная парабола. Полагая 
и 
, находим значения усилий в этих точках.
При значения внутренних усилий 
а при : 
Отметим, что в шарнирах моменты всегда равны нулю. На эпюре при 
перерезывающая сила 
. Это признак экстремума на эпюре моментов. Вычислим при 
максимум изгибающего момента
Откладываем полученное значение на графике-эпюре и проводим через три точки параболу. По правилу зонтика и дождика выпуклость параболы обращена к верху, а на перевернутой эпюре моментов – к низу. Эпюра моментов напоминает изогнутую ось балки, изображенную на рис. а пунктиром.
Пример 3.
Построить эпюры Qy, Mx для балки (см. рис. а).
а) б)
Решение.
Методом сечений (рис. б) находим
Поскольку
то эпюра – квадратичная парабола, а – кубическая.
При , 
. При имеем 
. Эпюра испытывает экстремум при 
, когда 
Выпуклость эпюры определяется знаком ее второй производной:
Так как вторая производная возрастает, то выпуклость направлена вниз.
Экстремум эпюры моментов имеет место в сечении, где 
, т.е. на конце консоли при . В этом сечении 
. Выпуклость кривой определяется по знаку второй производной, то есть по правилу зонтика:
В нашем случае выпуклость направлена вверх.
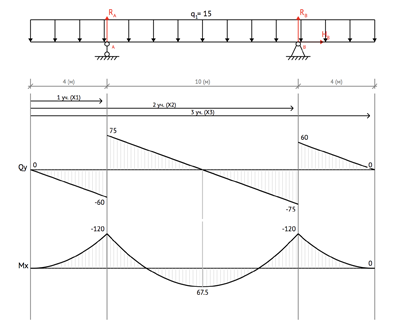
Пример 4.
Построить эпюры перерезывающих сил и изгибающих моментов Qy, Mx для балки (см. рис. а), если 
, интенсивность нагрузки 
.
а)
б)
Решение.
1. Определение опорных реакций из уравнений равновесия
Составим два независимых уравнения равновесия моментов относительно опор A, B:
Находим опорные реакции
Для статической проверки составляем третье зависимое уравнение равновесия в проекции на вертикальную ось:
Подставляем в это уравнение значения найденных реактивных сил и получаем
Следовательно, опорные реакции определены правильно.
2. Определение Qy, Mx методом сечения и построение их эпюр
Балка имеет два участка AC и CB с различными аналитическими выражениями внутренних силовых факторов.
На первом участке (рис. б) методом сечений с учетом 
находим
Эпюра − квадратичная парабола, а − кубическая.
При z1=0 имеем 
, а при z1=2а имеем 
. Согласно дифференциальным зависимостям Журавского экстремум эпюры Qy имеет место в сечении 
, где q=0, экстремум эпюры Mx в сечении, где Qy1=0 , что даёт 
,
На втором участке (рис. б) методом сечений получаем
При z2=3a Mx2=0 . Эпюра Qy − постоянна, а Mk − наклонная прямая. Максимальный момент определяется по формуле
3. Расчёт на прочность
Условие прочности записываем в виде
Пример 5.
Для заданной балки (см. рис.) построить эпюры от силы Q и от момента М.
Дано: l1=3,8 м; l2=3,6 м; l3=1,4 м, F=3,8q; M=14,44q
Решение.
Рассмотрим сечение 1-1: 
Рассмотрим сечение 2-2: 
Рассмотрим сечение 3-3: 
Пример 6.
Для заданной балки (см. рис.) построить эпюры от силы Q и от момента М.
Дано: l1=3,8 м; l2=3,6 м; l3=1,4 м, F=3,8q; M=14,44q
Решение.
Рассмотрим сечение 1-1: 
Рассмотрим сечение 2-2: 
Пример 7.
Для заданной балки (см. рис.) построить эпюры от силы Q и от момента М.
Дано: l1=3,8 м; l2=3,6 м; l3=1,4 м, F=3,8q; M=12,96q
Решение.
Находим реакции опор
Проверка
Реакции опор найдены правильно.
Рассмотрим сечение 1-1:
Рассмотрим сечение 2-2:
Рассмотрим сечение 3-3:
Пример 8.
Для заданной балки (см. рис.) построить эпюры от силы Q и от момента М.
Дано: l1=2 м; l2=3,4 м; l3=2 м, F=3,4q; M=4q
Решение.
Рассмотрим сечение 1-1: 
Рассмотрим сечение 2-2: 
Рассмотрим сечение 3-3: 
Пример 9.
Для заданной балки (см. рис.) построить эпюры от силы Q и от момента М
Дано: l1=2 м; l2=3,4 м; l3=2 м, F=2q; M=11,56q
Решение.
Находим реакции опор
Проверка