Расчетные сопротивления сжатия растяжения изгиба
При расчёте на прочность деревянных конструкций необходимо знать его расчётное сопротивление. Для деревянных конструкций есть несколько типов расчётных сопротивлений: на изгиб, сжатие, смятие, скол вдоль и поперёк волокон, растяжение вдоль и поперёк волокон, сжатие и смятие поперек волокон. Вначале рассмотрим, как вычисляется расчётное сопротивление деревянных конструкций, затем рассмотрим его расчёт на примере вычисления расчётного сопротивления на изгиб для доски балки перекрытия.
Методика расчёта взята из СП 64.133330.2017, который можно скачать по этой ссылке.
Расчётное сопротивление древесины определяем по формуле 1 СП
64.13330.2017:
где RA
– расчётное сопротивление древесины согласно таблицы 3 СП 64.13330.2017 в
зависимости от сечения и сорта древесины
Таблица 3 СП 64.13330.2017:
| Напряженное состояние и характеристика элементов | Расчетное сопротивление, МПа, для сортов древесины | |||
|---|---|---|---|---|
| Обозначение | 1 | 2 | 3 | |
| 1 Изгиб, сжатие и смятие вдоль волокон: | ||||
| а) элементы прямоугольного сечения [за исключением указанных в б), в)] высотой не более 50 см. При высоте сечения более 50 см [см. 6.9в)] | 21 | 19,5 | 13 | |
| б) элементы прямоугольного сечения шириной от 11 до 13 см при высоте сечения от 11 до 50 см | 22,5 | 21 | 15 | |
| в) элементы прямоугольного сечения шириной более 13 см при высоте сечения от 13 до 50 см | 24 | 22,5 | 16,5 | |
| г) элементы из круглых лесоматериалов без врезок в расчетном сечении | — | 24 | 15 | |
| 2 Растяжение вдоль волокон: | ||||
| а) элементы из цельной древесины | 15 | 10,5 | — | |
| б) клееные элементы | 18 | 13,5 | — | |
| 3 Сжатие и смятие по всей площади поперек волокон | 2,7 | 2,7 | 2,7 | |
| 4 Смятие поперек волокон местное: | ||||
| а) в опорных частях конструкций, лобовых врубках и узловых примыканиях элементов | 4,5 | 4,5 | 4,5 | |
| б) под шайбами при углах смятия от 90° до 60° | 6 | 6 | 6 | |
| 5 Скалывание вдоль волокон: | ||||
| а) при изгибе элементов из цельной древесины | 2,7 | 2,4 | 2,4 | |
| б) при изгибе клееных элементов | 2,4 | 2,25 | 2,25 | |
| в) в лобовых врубках для максимального напряжения | 3,6 | 3,2 | 3,2 | |
| г) местное в клеевых соединениях для максимального напряжения | 3,2 | 3,2 | 3,2 | |
| 6 Скалывание поперек волокон в соединениях: | ||||
| а) элементов из цельной древесины | 1,5 | 1,2 | 0,9 | |
| б) клееных элементов | 1,05 | 1,05 | 0,9 | |
| 7 Растяжение поперек волокон элементов из клееной древесины | 0,23 | 0,15 | 0,12 | |
| 8 Срез под углом к волокнам 45° | 9 | 7,5 | 6 | |
| То же 90° | 16,5 | 13,5 | 12 | |
| Примечания: | ||||
| 1 В конструкциях построечного изготовления величины расчетных сопротивлений на растяжение, принятые по пункту 2а) настоящей таблицы, следует снижать на 30%. | ||||
| 2 Расчетное сопротивление изгибу для элементов настила и обрешетки под кровлю из древесины 3-го сорта следует принимать равным 13 МПа. | ||||
Расчетные сопротивления для
других пород древесины устанавливают путем умножения величин, приведенных в
таблице 3, на переходные коэффициенты mп, указанные
в таблице 5.
Таблица 5 СП 64.13330.2017
| Древесная порода | Коэффициент mп для расчетных сопротивлений | ||
|---|---|---|---|
| растяжению, изгибу, сжатию и смятию вдоль волокон RP , RИ , RС ,RСМ | сжатию и смятию поперек волокон RС90 , RСМ90 | скалыванию RСК | |
| Хвойные | |||
| 1 Лиственница, кроме европейской | 1,2 | 1,2 | 1 |
| 2 Кедр сибирский, кроме кедра Красноярского края | 0,9 | 0,9 | 0,9 |
| 3 Кедр Красноярского края | 0,65 | 0,65 | 0,65 |
| 4 Пихта | 0,8 | 0,8 | 0,8 |
| Твердые лиственные | |||
| 5 Дуб | 1,3 | 2 | 1,3 |
| 6 Ясень, клен, граб | 1,3 | 2 | 1,6 |
| 7 Акация | 1,5 | 2,2 | 1,8 |
| 8 Береза, бук | 1,1 | 1,6 | 1,3 |
| 9 Вяз, ильм | 1 | 1,6 | 1 |
| Мягкие лиственные | |||
| 10 Ольха, липа, осина, тополь | 0,8 | 1 | 0,8 |
| Примечание – Коэффициенты mп, указанные в таблице, для конструкций опор воздушных линий электропередачи, изготавливаемых из не пропитанной антисептиками лиственницы (при влажности 25%), умножаются на коэффициент 0,85. | |||
mДЛ – коэффициент
длительной прочности, принимаемый по таблице 4 СП 64.13330.2017 в зависимости и
того, для чего служит конструкция
Таблица 4 СП 64.13330.2017
| Обозначение режимов нагружения | Характеристика режимов нагружения | Приведенное расчетное время действия нагрузки, с | Коэффициент длительной прочности mДЛ |
| А | Линейно возрастающая нагрузка при стандартных машинных испытаниях | 1-10 | 1,0 |
| Б | Совместное действие постоянной и длительной временной нагрузок, напряжение от которых превышает 80% полного напряжения в элементах конструкций от всех нагрузок | 108-109 | 0,53 |
| В | Совместное действие постоянной и кратковременной снеговой нагрузок | 106-107 | 0,66 |
| Г | Совместное действие постоянной и кратковременной ветровой и (или) монтажной нагрузок | 103-104 | 0,8 |
| Д | Совместное действие постоянной и сейсмической нагрузок | 10-102 | 0,92 |
| Е | Действие импульсивных и ударных нагрузок | 10-1-10-8 | 1,1-1,35 |
| Ж | Совместное действие постоянной и кратковременной снеговой нагрузок в условиях пожара | 103-104 | 0,8 |
| И | Для опор воздушных линий электропередачи — гололедная, монтажная, ветровая при гололеде, от тяжения проводов при температуре ниже среднегодовой | 104-105 | 0,85 |
| К | Для опор воздушных линий электропередачи — при обрыве проводов и тросов | 10-1-10-2 | 1,1 |
Пmi
– произведение коэффициентов условий работ согласно п.6.9 СП 64.13330.2017.
Рассмотрим все коэффициенты:
п.6.9 а) для различных условий эксплуатации конструкций –
коэффициент mВ, указанный в таблице
9:
Таблица 9 СП 64.13330.2017
| Условие эксплуатации (таблица 1) | 1А и 1 | 2 | 3 | 4 |
| Коэффициент mВ | 1 | 0,9 | 0,85 | 0,75 |
Условия эксплуатации указаны в таблице 1 СП 64.13330.2017
Таблица 1 СП 64.13330.2017
| Класс условий эксплуатации | Эксплуатационная влажность древесины, % | Максимальная относительная влажность воздуха при температуре 20°С, % | |
| 1 (сухой) | 1а | Не более 8 | 40 |
| 1б | Не более 10 | 50 | |
| 2 (нормальный) | Не более 12 | 65 | |
| 3 (влажный) | Не более 15 | 75 | |
| 4 (мокрый) | 4а | Не более 20 | 85 |
| 4б | Более 20 | Более 85 | |
| Примечания 1 Допускается в качестве «эксплуатационной» принимать «равновесную» влажность древесины (рисунок А.1 Приложения А СП 64.13330.2017). 2 Допускается кратковременное превышение максимальной влажности в течение 2-3 нед. в году. | |||
п.6.9 б) конструкций,
эксплуатируемых при установившейся температуре воздуха ниже плюс 35°С, —
коэффициент mТ=1; при температуре
плюс 50°С – коэффициент mТ=0,8. Для промежуточных
значений температуры коэффициент принимают по интерполяции;
п.6.9 в) изгибаемых,
внецентренно сжатых, сжато-изгибаемых и сжатых клееных элементов прямоугольного
сечения высотой более 50 см значения расчетных сопротивлений изгибу и сжатию
вдоль волокон – коэффициент mб,
указанный в таблице 10:
Таблица 10 СП 64.13330.2017
| Высота сечения, см | 50 и менее | 60 | 70 | 80 | 100 | 120 и более |
| Коэффициент mб | 1 | 0,96 | 0,93 | 0,90 | 0,85 | 0,8 |
п.6.9 г) растянутых элементов с
ослаблением в расчетном сечении и изгибаемых элементов из круглых
лесоматериалов с подрезкой в расчетном сечении – коэффициент mо=0,8;
п.6.9 д) элементов, подвергнутых глубокой пропитке
антипиренами под давлением, — коэффициент mа=0,9;
п.6.9 е) изгибаемых,
внецентренно сжатых, сжато-изгибаемых и сжатых клееных деревянных элементов, в
зависимости от толщины слоев, значения расчетных сопротивлений изгибу,
скалыванию и сжатию вдоль волокон — коэффициент mСД,
указанный в таблице 11:
Таблица 11 СП 64.13330.2017
| Толщина слоя, мм | 10 и менее | 19 | 26 | 33 | 42 |
| Коэффициент mСД | 1,2 | 1,1 | 1,05 | 1,0 | 0,95 |
п.6.9 ж) гнутых элементов
конструкций значения расчетных сопротивлений растяжению, сжатию и изгибу —
коэффициент mГН, указанный в таблице
12:
Таблица 12 СП 64.13330.2017
| Напряженное состояние | Обозначение расчетных сопротивлений | Коэффициент mГН при отношении rK/a | |||
| 150 | 200 | 250 | 500 и более | ||
| Сжатие и изгиб | Rc, Rи | 0,8 | 0,9 | 1 | 1 |
| Растяжение | Rр | 0,6 | 0,7 | 0,8 | 1 |
| Примечание — rK — радиус кривизны гнутой доски или бруска; a — толщина гнутой доски или бруска в радиальном направлении. | |||||
п. 6.9 и) в зависимости от срока
службы – коэффициент mc.c, указанный в таблице 13:
Таблица 13 СП 64.13330.2017
| Вид напряженного состояния | Значение коэффициента mc.c при сроке службы сооружения | ||
| ≤50 лет | 75 лет | 100 лет и более | |
| Изгиб, сжатие, смятие вдоль и поперек волокон древесины | 1,0 | 0,9 | 0,8 |
| Растяжение и скалывание вдоль волокон древесины | 1,0 | 0,85 | 0,7 |
| Растяжение поперек волокон древесины | 1,0 | 0,8 | 0,5 |
| Примечание — Значение коэффициента mc.c для промежуточных сроков службы сооружения принимаются по линейной интерполяции. | |||
п. 6.9 к) для смятия поперек
волокон при режимах нагружения Г-К (таблица 4, приведена выше) — коэффициент mcм=1,15.
Пример расчёта
расчётного сопротивления
Для примера рассмотрим расчёт расчётного сопротивления на
изгиб для балки из доски сечением 50х200 из сосны 1-го сорта.
RAИ=21
МПа (п.1а таблицы 30)
mДЛ =0,53 (режим Б
таблицы 4)
mв=0,9 коэффициент для
условий эксплуатации подбирается по таблице 9 СП 64.13330.2017 согласно
условиям эксплуатации по таблице 1 СП 64.13330.2017. При влажности воздуха до
65% (для жилых помещений) данный коэффициент равен 0,9
mT =1– коэффициент
условий работы при температуре эксплуатации для температуры ниже +35°С равен
единице.
mб =1 коэффициент условий
работы в зависимости от высоты сечения при высоте сечения ниже 50 см равен 1.
mо – не применяется т.к.
наша конструкция не относится к ситуациям п.6.9 г.
mа— не применяется т.к.
доску мы не пропитываем антипиренами;
mСД – не применяется т.к.
данный коэффициент используется для клееных элементов;
mГН – не применяется т.к.
данный коэффициент используется для гнутых элементов;
mc.c =1
коэффициент условий работы для срока службы менее 50 лет. Срок службы здания
регламентирован ГОСТ 27751-2014 Надежность строительных конструкций и оснований
Таблица 1. Для здания и сооружений массового строительства в обычных условиях
эксплуатации (здания жилищно-гражданского и производственного строительства)
принимается не менее 50 лет.
mcм – не применяется т.к. в нашем
случае режим нагружения будет Б.
Итого Пmi
равен:
Пmi=
mв*mT*mб*mc.c =0,9*1*1*1=0,9
Вычисляем расчётное сопротивление изгибу:
Rи=RAИ *mДЛ*Пmi=21*0,53*0,9=10,017 МПа
Источник
Сложное сопротивление – одновременное действие на брус нескольких простых видов деформаций: растяжения-сжатия, сдвига, кручения и изгиба. Например, совместное действие растяжения и кручения.
Косой изгиб.
Косой изгиб – это изгиб, при котором плоскость действия изгибающего момента не совпадает ни с одной из главных плоскостей инерции сечения бруса.
В общем случае при косом изгибе в поперечных сечениях возникают четыре внутренних силовых фактора: поперечные силы Qx, Qy и изгибающие моменты Mx , My. Таким образом, косой изгиб можно рассматривать как сочетание двух плоских поперечных изгибов во взаимно перпендикулярных плоскостях. Влиянием поперечных сил на прочность и жесткость бруса обычно пренебрегают.

Нейтральная линия при косом изгибе всегда проходит через центр тяжести сечения.
Условие прочности при косом изгибе:
где ymax, xmax — координаты точки сечения, наиболее удаленной от нейтральной оси.
Для сечений, имеющих две оси симметрии, максимальные напряжения будут в угловых точках, а условие прочности:
где Wx , Wy – осевые моменты сопротивления сечения относительно соответствующих осей.
Если материал бруса не одинаково работает на растяжение и на сжатие, то проверку его прочности выполняют по допускаемым и растягивающим и сжимающим напряжениям.
Прогибы при косом изгибе определяют, используя принцип независимости действия сил, геометрическим суммированием прогибов вдоль направления главных осей:
Изгиб с растяжением (сжатием).
При таком виде сложного сопротивления внутренние силовые факторы приводятся к одновременному действию продольной силы N и изгибающего момента M.
Рассмотрим случай центрального растяжения бруса в сочетании с косым изгибом. На консольный брус действует сила F, составляющая некоторый угол с продольной осью бруса и не лежащая ни в одной из главных плоскостей сечения. Сила приложена в центре тяжести торцевого сечения бруса:

К расчёту на прочность бруса при изгибе с растяжением:
a — нагружение бруса; б — внутренние силовые факторы в поперечном сечении;
Разложим силу F на три составляющие. Тогда внутренние силовые факторы приобретут следующий вид:
Напряжение в произвольно выбранной точке Д, имеющей координаты (хд, уд), пренебрегая действием поперечных сил, будут определяться по формуле:
где А — площадь поперечного сечения.
Если сечение имеет две оси симметрии (двутавр, прямоугольник, круг), наибольшее напряжение определяют по формуле:
Условие прочночти имеет вид:
Также как и в случае косого изгиба, если материал бруса не одинаково работает на растяжение и на сжатие, то проверку прочности проводят по допускаемым растягивающим и сжимающим напряжениям.
Внецентренное растяжение или сжатие.
При таком виде сложного сопротивления продольная сила приложена не в центре тяжести поперечного сечения бруса.

К расчёту на прочность бруса при внецентренном растяжении
a — нагружение бруса; б — внутренние силовые факторы в поперечном сечении;
Приведём силу F к центру тяжести:
где уF , xF — координаты точки приложения силы F.
В произвольной точке Д, с координатами (хд, уд), нормальное напряжение определяется по фомуле:
Условие прочности для бруса, изготовленного из материала, одинаково сопротивляющегося растяжению и сжатию, имеет вид:
Для бруса, который неодинаково работает на растяжение и на сжатие проверка прочности по допускаемым растягивающим и сжимающим напряжениям.
Кручение с изгибом.
Сочетание деформаций изгиба и кручения характерно для работы валов машин.

Напряжения в сечениях вала возникают от кручения и от изгиба. При изгибе появляются нормальные и касательные напряжения:

Эпюры напряжений в сечении бруса при кручении с изгибом
Нормальное напряжение достигает максимума на поверхности:
Касательное напряжение от крутящего момента Mz достигает максимума также на поверхности вала:
Из третьей и четвёртой теории прочности:
При кручении с изгибом условие прочности имеет вид:
Источник
Эта статья будет посвящена расчетам на прочность, которые выполняются в сопромате и не только. Расчеты на прочность бывают двух видов: проверочные и проектировочные (проектные).
Проверочные расчеты на прочность – это такие расчеты, в ходе которых проверятся прочность элемента заданной формы и размеров, под некоторой нагрузкой.
В ходе проектировочных расчетов на прочность определяются какие-то размеры элемента из условия прочности. Причем, очевидно, что для разных видов деформаций эти условия прочности различны. Также к проектным расчетам можно отнести расчеты на грузоподъемность, когда вычисляется максимальная нагрузка, которую может выдерживать конструкция, не разрушаясь. Рассмотрим более подробно, как проводится прочностные расчеты для разных случаев.
Расчеты на прочность при растяжении (сжатии)
Начнем, пожалуй, с самого простого вида деформации растяжения (сжатия). Напряжение при центральном растяжении (сжатии) можно получить, разделив продольную силу на площадь поперечного сечения, а условие прочности выглядит вот так:

где сигма в квадратных скобках – это допустимое напряжение. Которое можно получить, разделив предельное напряжения на коэффициент запаса прочности:

Причем, за предельное напряжение для разных материалов принимают разное значение. Для пластичных материалов, например, для малоуглеродистой стали (Ст2, Ст3) принимают предел текучести, а для хрупких (бетон, чугун) берут в качестве предельного напряжения – предел прочности (временное сопротивление). Эти характеристики получают при испытании образцов на растяжение или сжатие на специальных машинах, которые фиксируют характеристики в виде диаграммы.

Коэффициент запаса прочности выбирается конструктором исходя из своего личного опыта, назначения проектируемой детали и сферы применения. Обычно, он варьируется от 2 до 6.
В случае если необходимо подобрать размеры сечения, площадь выражают таким образом:

Таким образом, минимальная площадь поперечного сечения при центральном растяжении (сжатии) будет равна отношению продольно силы к допустимому напряжению.
Расчеты на прочность при кручении
При кручении расчеты на прочность в принципе схожи с теми, что проводятся при растяжении. Только здесь вместо нормальных напряжений появляются касательные напряжения.
На кручение работают, чаще всего, детали, которые называются валами. Их назначение заключается в передаче крутящего момента от одного элемента к другому. При этом вал по всей длине имеет круглое поперечное сечение. Условие прочности для круглого поперечного сечения можно записать так:

где Ip — полярный момент сопротивления, ρ — радиус круга. Причем по этой формуле можно определить касательное напряжение в любой точке сечения, варьируя значение ρ. Касательные напряжения распределены неравномерно по сечению, их максимальное значение находится в наиболее удаленных точках сечения:

Условие прочности, можно записать несколько проще, используя такую геометрическую характеристику как момент сопротивления:

То бишь максимальные касательные напряжения равны отношению крутящего момента к полярному моменту сопротивления и должны быть меньше либо равны допустимому напряжению. Геометрические характеристики для круга, упомянутые выше можно найти вот так:

Иногда в задачах встречаются и прямоугольные сечения, для которых момент сопротивления определяется несколько сложнее, но об этом я расскажу в другой статье.
Расчеты на прочность при изгибе
Источник
Примеры соединений, работающих на изгиб, показаны на рис. 4.11 а, б. Если шов выполнен с подготовкой кромок (рис. 4.11.а), то его размеры (расчетная толщина шва) не отличаются от размеров привариваемой полосы. Поэтому напряжения в шве при действии только изгибающего момента М определяются по формуле
σ = М/W ≤ [ σ’]р, (4.23)
где W = s·h2/6; [σ’]р — допускаемое напряжение растяжения сварного соединения;
М — изгибающий момент.
При действии изгибающего момента М и продольной силы Р (рис. 4.11 а, б)
σ = М/W + Р/F, (4.24)
где F = s·h.
Если полоса приварена двумя вертикальными угловыми швами (рис. 4.11 б), то напряжение в плоскости прикрепления О — О (рис. 4.11 в) будет
σ = М/Wс, (4.25)
где Wс — момент сопротивления угловых швов. В плоскости О — О момент сопротивления двух сварных швов высотой h и катетом К равен
Wс = Кh²/6. (4.26)
При этом следует иметь в виду два обстоятельства.
Во-первых, разрушение угловых швов обычно происходит не по плоскости О – О, а по направлению линии ОА, проходящей под углом 45° к плоскости привариваемой полосы.
Поэтому расчетный момент сопротивления угловых швов принимают по меньшему сечению; он будет равен
Wс = 2βКh²/6 (4.27)
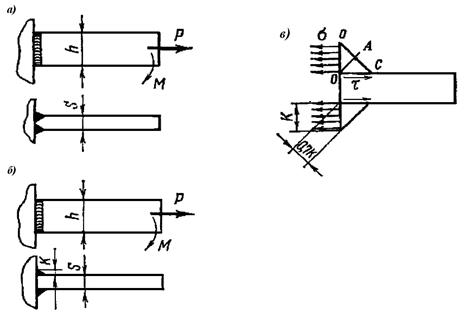
Рис. 4.11. Схема соединений:
а, б – швы, работающие на сложное сопротивление, в том числе на изгиб;
в — схема нагружения углового шва
Во-вторых, расчет прочности швов следует производить не по допускаемым нормальным напряжениям (плоскости О — О), а по напряжениям на косой плоскости (линия ОА). Значение этих напряжений ограничивают допускаемым напряжением на срез [τ’]. Таким образом, расчетное напряжение в швах (рис. 4.11 б) от момента М определяют по формуле
τ = М/ Wс ≤ [ τ’]. (4.28)
При действии в этом соединении момента М и продольной силы Р расчетное касательное напряжение в угловых швах (рис. 4.11 б) равно
τ = М/ Wс +Р/ Fс ≤ [ τ’]. (4.29)
где Fс — площадь сечения угловых швов.
В швах, имеющих форму равнобедренного треугольника минимальная толщина, как бисектрисса прямого угла, будет равна 0,7 К, а площадь среза двух угловых швов Fс =2·0,7 К·h.
Рассмотрим расчет прочности швов, лежащих в плоскости изгибающего момента (рис. 4.12).
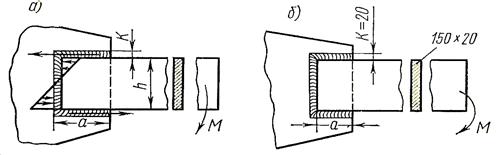
Рис. 4.12. Сварные соединения в плоскости изгибающего момента М: а – схема расчета швов; б – пример расчета по способу расчленения соединения
Расчет прочности проведем по способу расчленения соединения на составляющие. Принимаем, что момент М уравновешивается моментом пары сил в горизонтальных швах Мг и моментом защемления вертикального шва Мв (рис. 4.12 а):
М = Мг + Мв. (4.30)
Допустим, что швы имеют форму равнобедренного треугольника. В горизонтальных швах образуется пара сил. Ее момент равен
Мг = τβКа(h + К). (4.31)
Момент в вертикальном шве вычисляем по формуле
Мв = τβКh² /6. (4.32)
По формуле (3.43),
М = τβКа(h + К) + τβКh²/6, (4.33)
откуда касательное напряжение равно
τ = М/[βКа(h + К) + τβКh² /6] ≤ [τ’ ]. (4.34)
Пользуясь уравнением (3.47) при конструировании соединения, легко определить требуемую длину швов а или катет К.
Пример расчета. Сконструировать прикрепление полосы сечением 150Х20 мм вертикальными и горизонтальными швами, равнопрочное целому элементу при изгибе (рис. 4.12 б), допускаемое напряжение [σ]р; сварка полуавтоматическая (β = 0,8); [τ’] = 0,65 [σ]р.
Момент, допускаемый в полосе, равен М = [σ]р W = [σ]р sh²/6.
Момент, допускаемый в вертикальном шве при К = 20 мм и τ’ == 0,65 [σ]р,
равен
М = 0,65 [σ]р βКh²/6,
Момент, допускаемый в горизонтальных швах, вычисляется по формуле
Мr = М — Мв.
Усилие на один горизонтальный шов равно Рг = Мг/( h + К) = =[σ]р h² (s — 0,52К)/[6(h + К)].
Требуемая длина горизонтального шва при К = 20 мм определяется по формуле
а = Рг /[ τ’ ] βК =[σ]р h² (s — 0,52К)/[3,12 [σ]р (К + h) К ]≈0,02 м.
Из конструктивных соображений можно принять а = 50 мм.
При рассмотрении прочности прикреплений элементов, работающих на изгиб, будем предполагать, что угловые швы имеют форму равнобедренного треугольника. Расчет прочности производится на срез в плоскости, совпадающей с биссектрисой прямого угла и равной по площади βКа, где К — катет шва, а — длина шва.
Определим напряжения в сварном соединении, прикрепляющем балку прямоугольного поперечного сечения, работающую на изгиб, относительно оси х- х (рис. 4.13, а).
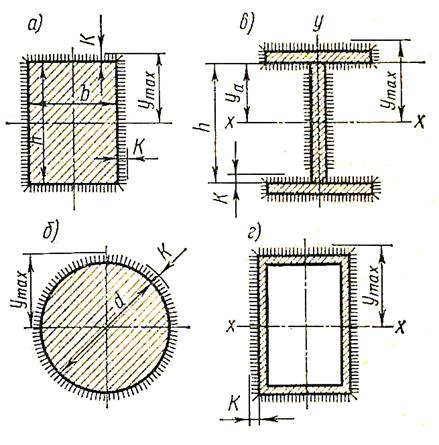
Рис. 4.13. Сварные соединения элементов, обваренных по периметрам угловыми швами: а – прямоугольное сечение; б – круглое сечение; в – двутавровое сечение; г – коробчатое сечение
Соединение сконструировано с угловыми швами, охватывающими профиль по периметру. Нормальные напряжения в балке вызывают касательные напряжения τ в швах:
τ = М/Wc ≤ [τ’]. (4.35)
Момент сопротивления
Wс = Iс/ymax, (4.36)
где Iс — расчетный момент инерции периметра швов относительно оси Х-Х. С учетом возможного разрушения по наименьшему сечению Iс = I·β,
где I — момент инерции периметра швов, т. е.
Iс = β {2Кb [(h + К)/2]² + 2К³b/12 + 2К (h + 2К)³/12}; (4.37)
ymax = h/2+К. (4.38)
Для круглого поперечного сечения (рис. 4.13 б)
Iс = β [π (d + 2К)4/64 — πd4/64]; (4.39)
ymax = d/2+К. (4.40)
Расчет прочности прикрепления произвольных профилей двутавровых, коробчатых (рис. 4.13 е, г), тавровых и других производится так же, как в случаях, рассмотренных выше, на основе формул (4.35) и (4.36).
Если элемент работает при сложном сопротивлении — изгибающем моменте М и продольной силе N, то суммарное напряжение в соединении равно
τ = (4.41)
где Fc – расчетная площадь среза всех сварных швов:
Fc = β·K·L, (4.42)
где L – длина периметра сварных швов.
Если элементы нагружены поперечными нагрузками, то в них возникают изгибающие моменты М и поперечные силы Q. Напряжения в сварных швах от действия силы Q определяют с учетом следующих допущений: поперечная сила воспринимается только вертикальными швами, распределение напряжений по длине вертикальных швов равномерно. Таким образом, среднее напряжение в шве от поперечной силы равно
τQ = Q / FB, (4.43)
где FB — расчетная площадь вертикальных швов.
На уровне верхней кромки вертикального листа в швах следует проверить результирующие напряжения от действия момента и поперечной силы.
Напряжение от момента
τ1 = ya М / Ic, (4.44)
где ya — расстояние от оси, проходящей через центр тяжести сечения, до горизонтальной верхней кромки (рис. 4.14).
Напряжение от поперечной силы
τQ = Q /(2βKh). (4.45)
Результирующее напряжение равно корню квадратному из суммы квадратов τ1 и τQ:
τрез = √τ1² + τQ² (4.46)
Практика расчетов показывает, что проверка прочности по формуле (4.35) является решающей.
Пример расчета.Консольная стальная балка двутаврового профиля (рис. 4.14) прикреплена по периметру угловыми швами с катетом К = 6 мм; продольная сила N = 50 кН; поперечная сила Q = 2,5 кН; сварка полуавтоматическая (β = 0,8) в среде СО2 проволокой Св-08Г2С с расчетным сопротивлением металла угловых швов Rwf =215 МПа.
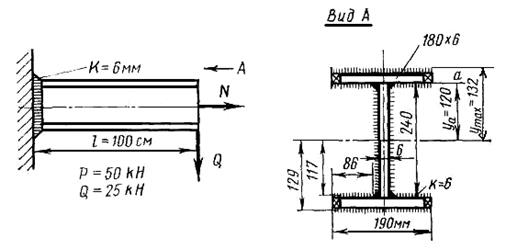
Рис.4.14. Расчет швов соединений при сложном сопротивлении
Момент инерции периметра угловых швов равен
I = 2 · 24³ · 0,6/12 +2 (19 · 0,6³/12 + 19 · 0,6 · 12,9²) + 2(2 · 8,6 · 0,6³/12 + 2 · 8,6 · 0,6· ·11,7²) = 8000 см4.
Расчетный момент инерции угловых швов с учетом разрушения по опасной плоскости (β = 0,8) Ic = β· I = 0,8 · 8000 = 6400 см4.
Ордината ya = 12 см. Площадь поперечного сечения всего периметра угловых швов F = 2 · 24 · 0,6 + 2 · 19 · 0,6 + 4 · 8,6 · 0,6=72,2 см².
Расчетная площадь всех сварных швов с учетом разрушения по опасной плоскости равна Fc = F·β = 0,8 · 72,2 = 57,7 см².
Расчетная площадь вертикальных швов с учетом разрушения по опасной плоскости будет F′с=2 · 0,8 · 0,6 · 24 ==23,0 см².
Напряжения от изгиба на крайней кромке вертикального листа равны
τ1=М·ya /Iс = 0,025 · 1 · 0,12 / (6400 · 10-8) = 47 МПа.
Напряжение от продольной силы в угловых швах соединения
τN = N / Fc = 0,05/(57,7 · 10-4) = 8,4 МПа.
Суммарное напряжение τ = 47 + 8,4 = 55,4 МПа.
Среднее касательное напряжение в вертикальных швах
τQ = 0,025 / 23 ·10-4 = 10,9 МПа.
Результирующее напряжение при ya= 12 см
τрез = √55,4² + 10,9² = 56,5 МПа.
Напряжение от изгиба при ymax = 13,2 см
τ = М·ymax / Ic = (0,025 · 1 / 6400 · 10 -8) · 0,132 = 51,6 МПа.
Суммарное напряжение от М и N при ymax = 13,2 см
τсумм = 51,6 + 8,4 = 60,0 МПа < Rwf =215 МПа.
Источник
