Расчетное сопротивление растяжению а500с
А500С — расшифровка обозначения: А — горячекатаная термически упрочненная, 500 — предел текучести, С — применима сварка
Арматура А500С ГОСТ 52544-2006, ГОСТ 34028-2016 (введен в действие 01.01.2019г.) – универсальная свариваемая строительная арматура новейшего класса. В РФ в 1993 году был разработан НИИЧЕРМЕТ и выпущен новый стандарт СТО АСЧМ 7-93, который регламентирует требования к арматуре класса А500С, позднее был разработан и внедрен ГОСТ 52544-2006.
Арматура стальная А500С благодаря своим свойствам — наиболее востребована при ведении строительных работ методом монолитного железобетона, а низкое содержание углерода наряду с термомеханической обработкой арматурной стали обеспечивает ее улучшенную свариваемость и пластичность, повышенную вязкость и долговечность.
| 1 | Стальная арматура класса А500С ГОСТ 52544-2006 и ГОСТ 34028-2016 — является свариваемой, о чём свидетельствует буква «С» которая присутствует в ее маркировке — одно из важных преимуществ это возможность использовать дуговую сварку при работе. |
| 2 | Арматура изготовляется из стали 3ПС и содержит значительно меньше легирующих компонентов, чем сталь марки 35ГС или 25Г2С, что позволяет изгибать стержни на значительные углы. |
| 3 | Универсальность — Госстрой России рекомендует применение арматуры А500С в железобетонных конструкциях наряду и взамен арматурной стали классов A-III или А400 марки стали 35ГС (ГОСТ 5781-82) и Ат-IIIС (ГОСТ 10884-81) тех же диаметров. |
Письмо Госстроя России 
ПРОФИЛЬ АРМАТУРЫ КЛАССА А500С
Рис.1. Серповидный профиль ( ГОСТ 52544-2006, принят наряду и взамен СТО АСЧМ 7-93, новый ГОСТ 34028-2016 введен в действие с 01.01.2019)
Профиль отличается по внешнему виду от класса AIII (А400), прежде всего тем, что в профиле серповидные выступы не пересекаются с продольными ребрами. Серповидный профиль способствует формированию более высоких прочностных и пластических свойств стали при прокатке и не имеет концентраторов напряжений в местах пересечений поперечных ребер с продольными (они не пересекаются). Рисунок профиля у разных производителей, может иметь различные варианты исполнения, которые отличаются шагом, углом наклона серповидных выступов по отношению друг к другу.
ХАРАКТЕРИСТИКИ
| Нормативные документы, механические свойства, области применения, эффективность | Класс | ||
|---|---|---|---|
| А400 (А-III) | А500С | ||
| Марка стали | |||
| 35ГС | 25Г2С | 3ПС | |
| Нормативные документы для поставки | ГОСТ 5781-82, 34028-2016 | ГОСТ 34028-2016, 52544-2006 | |
| Нормативные документы для расчета и проектирования ЖБК | СНиП 2.03.01-84 | Рекомендации НИИЖБ | |
| Временное сопротивление разрыву σВ, Н/мм | 590 | 590 | 600 |
| Предел текучести σТ, Н/мм | 390 | 390 | 500 |
| Относительное удлинение σ5, % | 14 | 14 | 14 |
| Угол изгиба при диаметре оправки C=3d | 90° | 90° | 180° |
| Расчетное сопротивление растяжению при σ6,8 мм RS, Н/мм | 355 | 355 | 450 |
| Расчетное сопротивление растяжению при σ10-40 мм RS, Н/мм | 365 | 365 | 450 |
| Расчетное сопротивление сжатию RSC, Н/мм | — | — | 450 |
| Расчетное сопротивление RSC, Н/мм | 390 | 390 | 500 |
| Применение при отрицательных температурах | до -40°С | до -55°С | до -55°C |
| Применение дуговой сварки крестообразных соединений | Запрещено | Не рекомендуется | Допускается |
| Применение в качестве анкеров закладных деталей | Допускается | Повышенная надежность | |
| Применение в качестве монтажных петель | Запрещено | Возможно | |
| Возможный экономический эффект относительно класса А400 (А-III) | — | — | 10-25% |
ХИМИЧЕСКИЙ СОСТАВ СТАЛИ
| C | Si | Mn | Ni | S | P | Cr | N | Cu | As |
|---|---|---|---|---|---|---|---|---|---|
| 0,14-0,22 | 0,05-0,15 | 0,4-0,65 | до 0,3 | до 0,05 | до 0,04 | до 0,3 | до 0,008 | до 0,3 | до 0,08 |
Источник
Для примера построения диаграмм взят наиболее часто используемый класс бетона (В25) и арматуры (А500С).
Для расчетов по второму предельному состоянию.
При нормативной длительной нагрузке (для определения прогибов ж/б плит)
Трехлинейная диаграмма
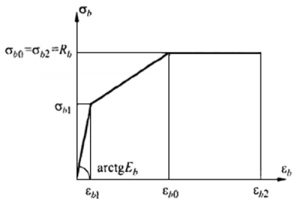
Рис. 1. Трехлинейная диаграмма состояния сжатого бетона из СП 63.13330
СП 63.13330.2012, п. 6.1.25: «При расчете деформаций железобетонных элементов по нелинейной деформационной модели при отсутствии трещин для оценки напряженно-деформированного состояния в сжатом и растянутом бетоне используют трехлинейную диаграмму состояния бетона с учетом непродолжительного и продолжительного действия нагрузки. При наличии трещин для оценки напряженно-деформированного состояния сжатого бетона помимо указанной выше диаграммы используют, как наиболее простую, двухлинейную диаграмму состояния бетона с учетом непродолжительного и продолжительного действия нагрузки«.
Расчетные значения сопротивления бетона осевому сжатию:
Rb = σb0 = σb2 = Rb,n = 18,5 МПа.
Начальный модуль упругости бетона при сжатии и растяжении:
Eb = 30000 МПа.
При продолжительном действии нагрузки модуль деформации бетона определяют по формуле:
Eb,t = Eb / 1 + φb,cr = 30000 / 1 + 2,5 = 8571,43 МПа;
Коэффициент φb,cr при нормальной влажности (40-75%) равен 2,5.
При трехлинейной диаграмме значения напряжений σb1 определяют по формуле:
σb1 = 0,6 х Rb,n = 11,1 МПа;
а значения относительных деформаций εb1 принимают:
εb1 = σb1 / Eb,t = 11,1 / 8571,43 = 0,001295.
Значения относительных деформаций εb2 для тяжелого бетона при продолжительном действии нагрузок принимают по таблице 6.10:
εb2 = 0,0048.
Значения предельных относительных деформаций εb0 тяжелого бетона при продолжительном действии нагрузок и нормальной влажности (40-75%) принимают по таблице 6.10:
εb0 = 0,0034.
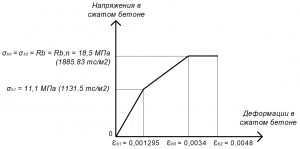
Рис. 2. Трехлинейная диаграмма состояния сжатого тяжелого бетона класса В25 по СП 63.13330 при нормативной длительной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому растяжению:
Rbt = σbt0 = σbt2 = Rbt,n = 1,55 МПа.
При трехлинейной диаграмме значения напряжений σbt1 определяют по формуле:
σbt1 = 0,6 х Rbt,n = 0,93 МПа;
При продолжительном действии нагрузки модуль деформации бетона определяют по формуле:
Eb,t = Eb / 1 + φb,cr = 30000 / 1 + 2,5 = 8571,43 МПа;
Значения относительных деформаций εbt1 принимают:
εbt1 = σbt1 / Eb,t = 0,93 / 8571,43 = 0,0001085.
Значения предельных относительных деформаций εbt0 тяжелого бетона при продолжительном действии нагрузок и нормальной влажности (40-75%) принимают по таблице 6.10:
εbt0 = 0,00024.
Значения относительных деформаций εbt2 для тяжелого бетона при продолжительном действии нагрузок принимают по таблице 6.10:
εbt2 = 0,00031.
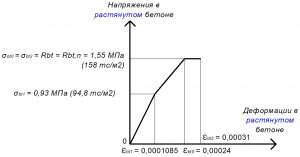
Рис. 3. Трехлинейная диаграмма состояния растянутого тяжелого бетона класса В25 по СП 63.13330 при нормативной длительной нагрузке и высоте бетонирования не более 1,5 м
Двухлинейная диаграмма
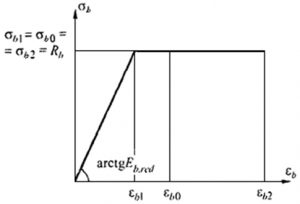
Рис. 4. Двухлинейная диаграмма состояния сжатого бетона из СП 63.13330
Расчетные значения сопротивления бетона осевому сжатию:
Rb = σb0 = σb1 = σb2 = Rb,n = 18,5 МПа.
Значения относительных деформаций εb2 для тяжелого бетона при продолжительном действии нагрузок:
εb2 = 0,0048.
Значения приведенного модуля деформации бетона Eb,red принимают:
Eb,red = Rb,n / εb1,red
Значения относительных деформаций εb1,red принимают по таблице 6.10:
при нормальной влажности (40-75%) εb1,red = 0,0028;
Eb,red = 18,5 / 0,0028 = 6607,14;
εb1 = Rb,n / Eb,red = 18,5 / 6607,14 = 0,0028.
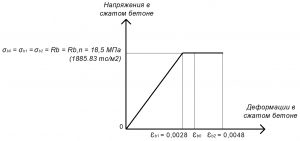
Рис. 5. Двухлинейная диаграмма состояния сжатого тяжелого бетона класса В25 по СП 63.13330 при нормативной длительной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому растяжению:
Rbt = σbt0 = σbt1 = σbt2 = Rbt,n = 1,55 МПа.
Значения относительных деформаций εbt2 для тяжелого бетона при продолжительном действии нагрузок принимают по таблице 6.10:
εbt2 = 0,00031.
Значения приведенного модуля деформации бетона Ebt,red принимают:
Ebt,red = Rbt,n / εbt1,red
Значения относительных деформаций εbt1,red принимают по таблице 6.10:
при нормальной влажности (40-75%) εbt1,red = 0,00022;
Ebt,red = 1,55 / 0,00022 = 7045,45;
εbt1 = Rbt,n / Ebt,red = 1,55 / 7045,45 = 0,00022.
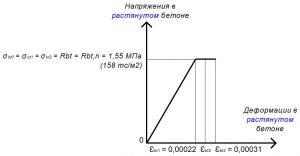
Рис. 6. Двухлинейная диаграмма состояния растянутого тяжелого бетона класса В25 по СП 63.13330 при нормативной длительной нагрузке и высоте бетонирования не более 1,5 м
Данные диаграммы построены для бетона при продолжительном действии нагрузок и могут использоваться при расчете прогибов. Для расчета ширины раскрытия трещин нужно строить диаграммы при непродолжительном действии нагрузок, см. п. 6.1.26 СП 63.13330: «При расчете раскрытия нормальных трещин по нелинейной деформационной модели для оценки напряженно-деформированного состояния в сжатом бетоне используют диаграммы состояния, приведенные в 6.1.20 и 6.1.21, с учетом непродолжительного действия нагрузки. При этом в качестве наиболее простой используют двухлинейную диаграмму состояния бетона».
Двухлинейная диаграмма состояния (деформирования) арматуры при нормативной длительной нагрузке
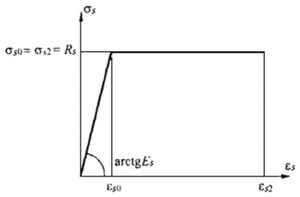
Рис. 7. Двухлинейная диаграмма состояния арматуры из СП 63.13330
Расчетное сопротивление растяжению арматуры Rs:
Rs = σs0 = σs2 = Rs,n = 500 МПа (для А500С).
Значения модуля упругости арматуры принимают одинаковыми при растяжении и сжатии и равными, для арматуры А500С:
Es = 200000 МПа.
Значения относительных деформаций арматуры εs0 принимают равными:
для арматуры с физическим пределом текучести
εs0 = Rs,n / Es = 500 / 200000 = 0,0025.
Значения относительной деформации εs2 принимают равными 0,025.
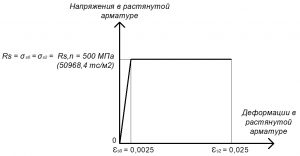
Рис. 8. Двухлинейная диаграмма состояния растянутой (или сжатой) арматуры класса А500С при длительной нормативной нагрузке
При расчете железобетонных элементов по нелинейной деформационной модели в качестве расчетной диаграммы состояния (деформирования) арматуры, устанавливающей связь между напряжениями σs и относительными деформациями εs арматуры, для арматуры с физическим пределом текучести классов А240-А500, В500 принимают двухлинейную диаграмму. Диаграммы состояния арматуры при растяжении и сжатии принимают одинаковыми, с учетом нормируемых расчетных сопротивлений арматуры растяжению и сжатию.
Для расчетов по второму предельному состоянию.
При полной нормативной нагрузке (для проверки ширины раскрытия трещин)
Трехлинейная диаграмма
Рис. 9. Трехлинейная диаграмма состояния сжатого бетона из СП 63.13330
Расчетные значения сопротивления бетона осевому сжатию:
Rb = σb0 = σb2 = Rb,n = 18,5 МПа.
Начальный модуль упругости бетона при сжатии и растяжении:
Eb = 30000 МПа.
При трехлинейной диаграмме значения напряжений σb1 определяют по формуле:
σb1 = 0,6 х Rb = 11,1 МПа;
а значения относительных деформаций εb1 принимают:
εb1 = σb1 / Eb = 11,1 / 30000 = 0,00037.
Значения относительных деформаций εb2 для тяжелого бетона при непродолжительном действии нагрузок принимают, для бетонов класса по прочности на сжатие В60 и ниже:
εb2 = 0,0035.
Значения предельных относительных деформаций εb0 тяжелого бетона при непродолжительном действии нагрузок:
εb0 = 0,002.
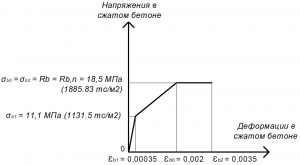
Рис. 10. Трехлинейная диаграмма состояния сжатого тяжелого бетона класса В25 по СП 63.13330 при полной нормативной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому растяжению:
Rbt = σbt0 = σbt2 = 1,55 МПа.
При трехлинейной диаграмме значения напряжений σbt1 определяют по формуле:
σbt1 = 0,6 х Rbt = 0,93 МПа;
Начальный модуль упругости бетона при сжатии и растяжении:
Eb = 30000 МПа.
Значения относительных деформаций εbt1 принимают:
εbt1 = σbt1 / Eb = 0,93 / 30000 = 0,000031.
Значения предельных относительных деформаций εbt0 тяжелого бетона при непродолжительном действии нагрузок:
εbt0 = 0,0001.
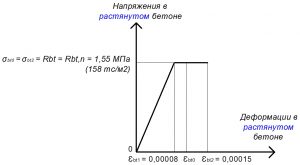
Значения относительных деформаций εbt2 для тяжелого бетона при непродолжительном действии нагрузок:
εbt2 = 0,00015.
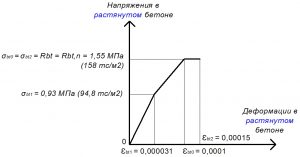
Рис. 11. Трехлинейная диаграмма состояния растянутого тяжелого бетона класса В25 по СП 63.13330 при полной нормативной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому сжатию:
Rb = σb0 = σb1 = σb2 = 18,5 МПа.
Значения относительных деформаций εb2 для тяжелого бетона при непродолжительном действии нагрузок принимают, для бетонов класса по прочности на сжатие В60 и ниже:
εb2 = 0,0035.
Значения приведенного модуля деформации бетона Eb,red принимают:
Eb,red = Rb / εb1,red
Значения относительных деформаций εb1,red принимают при непродолжительном действии нагрузки:
εb1,red = 0,0015;
Eb,red = 18,5 / 0,0015 = 12333,3;
εb1 = Rb / Eb,red = 18,5 / 12333,3 = 0,0015.
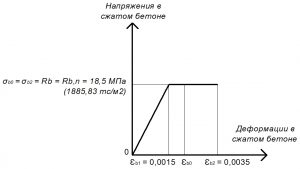
Рис. 12. Двухлинейная диаграмма состояния сжатого тяжелого бетона класса В25 по СП 63.13330 при полной нормативной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому растяжению:
Rbt = σbt0 = σbt1 = σbt2 = 1,55 МПа.
Значения относительных деформаций εbt2 для тяжелого бетона при непродолжительном действии нагрузок:
εbt2 = 0,00015.
Значения приведенного модуля деформации бетона Ebt,red принимают:
Ebt,red = Rbt / εbt1,red
Значения относительных деформаций εbt1,red принимают при непродолжительном действии нагрузок:
εbt1,red = 0,00008;
Ebt,red = 1,55 / 0,00008 = 19375;
εbt1 = Rbt / Ebt,red = 1,55 / 19375 = 0,00008.
Рис. 13. Двухлинейная диаграмма состояния растянутого тяжелого бетона класса В25 по СП 63.13330 при полной нормативной нагрузке и высоте бетонирования не более 1,5 м
Двухлинейная диаграмма состояния (деформирования) арматуры при полной нормативной нагрузке
Рис. 14. Двухлинейная диаграмма состояния арматуры из СП 63.13330
Расчетное сопротивление растяжению арматуры Rs:
Rs = σs0 = σs2 = 500 МПа (для А500С).
Расчетное сопротивление сжатию арматуры Rs:
Rsс = σsс0 = σsс2 = 500 МПа (для А500С).
Значения модуля упругости арматуры принимают одинаковыми при растяжении и сжатии и равными, для арматуры А500С:
Es = 200000 МПа.
Значения относительных деформаций растянутой арматуры εs0 принимают равными:
для арматуры с физическим пределом текучести
εs0 = Rs / Es = 500 / 200000 = 0,0025.
Значения относительных деформаций сжатой арматуры εsс0 принимают равными:
для арматуры с физическим пределом текучести
εsс0 = Rsс / Es = 500 / 200000 = 0,0025.
Значения относительной деформации εs2 принимают равными 0,025.
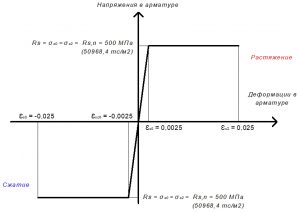
Рис. 15. Двухлинейная диаграмма состояния арматуры класса А500С при полной нормативной нагрузке
Для расчетов по первому предельному состоянию.
При полной расчетной нагрузке (для проверки прочности)
Трехлинейная диаграмма
Рис. 16. Трехлинейная диаграмма состояния сжатого бетона из СП 63.13330
Расчетные значения сопротивления бетона осевому сжатию:
Rb = σb0 = σb2 = 14,5 МПа.
Начальный модуль упругости бетона при сжатии и растяжении:
Eb = 30000 МПа.
При трехлинейной диаграмме значения напряжений σb1 определяют по формуле:
σb1 = 0,6 х Rb = 8,7 МПа;
а значения относительных деформаций εb1 принимают:
εb1 = σb1 / Eb = 8,7 / 30000 = 0,00029.
Значения относительных деформаций εb2 для тяжелого бетона при непродолжительном действии нагрузок принимают, для бетонов класса по прочности на сжатие В60 и ниже:
εb2 = 0,0035.
Значения предельных относительных деформаций εb0 тяжелого бетона при непродолжительном действии нагрузок:
εb0 = 0,002.
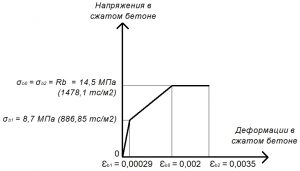
Рис. 17. Трехлинейная диаграмма состояния сжатого тяжелого бетона класса В25 по СП 63.13330 при полной расчетной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому растяжению:
Rbt = σbt0 = σbt2 = 1,05 МПа.
При трехлинейной диаграмме значения напряжений σbt1 определяют по формуле:
σbt1 = 0,6 х Rbt = 0,63 МПа;
Начальный модуль упругости бетона при сжатии и растяжении:
Eb = 30000 МПа.
Значения относительных деформаций εbt1 принимают:
εbt1 = σbt1 / Eb = 0,63 / 30000 = 0,000021.
Значения предельных относительных деформаций εbt0 тяжелого бетона при непродолжительном действии нагрузок:
εbt0 = 0,0001.
Значения относительных деформаций εbt2 для тяжелого бетона при непродолжительном действии нагрузок:
εbt2 = 0,00015.
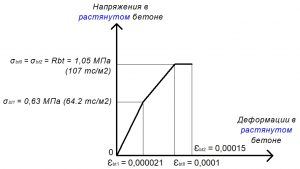
Рис. 18. Трехлинейная диаграмма состояния растянутого тяжелого бетона класса В25 по СП 63.13330 при полной расчетной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому сжатию:
Rb = σb0 = σb1 = σb2 = 14,5 МПа.
Значения относительных деформаций εb2 для тяжелого бетона при непродолжительном действии нагрузок принимают, для бетонов класса по прочности на сжатие В60 и ниже:
εb2 = 0,0035.
Значения приведенного модуля деформации бетона Eb,red принимают:
Eb,red = Rb / εb1,red
Значения относительных деформаций εb1,red принимают при непродолжительном действии нагрузки:
εb1,red = 0,0015;
Eb,red = 14,5 / 0,0015 = 9666,7;
εb1 = Rb / Eb,red = 14,5 / 9666,7 = 0,0015.
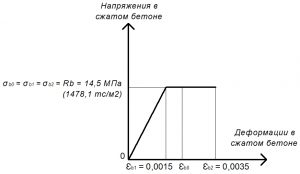
Рис. 19. Двухлинейная диаграмма состояния сжатого тяжелого бетона класса В25 по СП 63.13330 при полной расчетной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому растяжению:
Rbt = σbt0 = σbt1 = σbt2 = 1,05 МПа.
Значения относительных деформаций εbt2 для тяжелого бетона при непродолжительном действии нагрузок:
εbt2 = 0,00015.
Значения приведенного модуля деформации бетона Ebt,red принимают:
Ebt,red = Rbt / εbt1,red
Значения относительных деформаций εbt1,red принимают при непродолжительном действии нагрузок:
εbt1,red = 0,00008;
Ebt,red = 1,05 / 0,00008 = 13125;
εbt1 = Rbt / Ebt,red = 1,05 / 13125 = 0,00008.
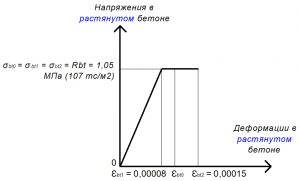
Рис. 20. Двухлинейная диаграмма состояния растянутого тяжелого бетона класса В25 по СП 63.13330 при полной расчетной нагрузке и высоте бетонирования не более 1,5 м
Двухлинейная диаграмма состояния (деформирования) арматуры при полной расчетной нагрузке
Рис. 21. Двухлинейная диаграмма состояния арматуры из СП 63.13330
Расчетное сопротивление растяжению арматуры Rs:
Rs = σs0 = σs2 = 430 МПа (для А500С).
Расчетное сопротивление сжатию арматуры Rs:
Rsс = σsс0 = σsс2 = 400 МПа (для А500С).
Значения модуля упругости арматуры принимают одинаковыми при растяжении и сжатии и равными, для арматуры А500С:
Es = 200000 МПа.
Значения относительных деформаций растянутой арматуры εs0 принимают равными:
для арматуры с физическим пределом текучести
εs0 = Rs / Es = 435 / 200000 = 0,002175.
Значения относительных деформаций сжатой арматуры εsс0 принимают равными:
для арматуры с физическим пределом текучести
εsс0 = Rsс / Es = 400 / 200000 = 0,002.
Значения относительной деформации εs2 принимают равными 0,025.
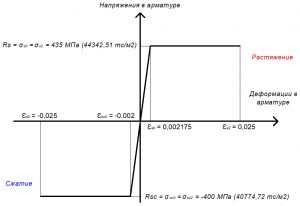
Рис. 22. Двухлинейная диаграмма состояния арматуры класса А500С при полной расчетной нагрузке
Ссылки по теме:
- Пример расчета нелинейного прогиба железобетонной балки по СП 63 в программе ЛИРА-САПР;
- Научно-методологические основы получения, описания, совершенствования и применения диаграмм деформирования бетона. Сравнительный анализ некоторых из известных по критерию энергозатрат. (Источник: «https://scadsoft.com/uploads/31«);
Источник
ТСН
102-00*
Дата введения 2000-02-01
ТСН 102-00* разработаны
по заказу ОАО «Московский комитет по науке и технологиям» (договор
N 7-С/04 от 31.05.2004 г.) и содержат изменения и дополнения,
полученные в результате проектно-конструкторских и
исследовательских работ, выполненных ГУП «НИИМосстрой» (ГУП НКТЦ),
ГУП «НИИЖБ» и ОАО «Моспромжелезобетон», а также практической работы
с применением положений ТСН 102-00, введенных в действие 01.01.2000
г.
Разделы, пункты, таблицы
и приложения, в которые внесены изменения, отмечены звездочкой.
ВВЕДЕНИЕ
При разработке настоящих
Территориальных строительных норм были учтены положения
отечественных и зарубежных норм и стандартов, результаты
научно-исследовательских работ, а также практический опыт
применения арматуры классов А500С и А400С в различных изделиях на
ряде предприятий промышленности сборного железобетона г.Москвы.
Данные ТСН не
противоречат требованиям СНиП
2.03.01-84* «Бетонные и железобетонные конструкции», содержат
ряд технических положений, не установленных в этих нормах, и
являются рекомендательным документом.
1.
ОБЛАСТЬ ПРИМЕНЕНИЯ
1.1 Настоящие нормы
распространяются на проектирование, технологию изготовления и
контроль качества железобетонных конструкций промышленных и
гражданских зданий и сооружений, выполненных с применением арматуры
классов А500С и А400С без предварительного напряжения. Конструкции
выполняются из тяжелых и легких бетонов плотной структуры,
воспринимают статические нагрузки и климатические воздействия
района г.Москвы и эксплуатируются в среде с неагрессивным и
агрессивным воздействием.
1.2 Настоящие нормы
следует применять совместно с СНиП
2.03.01-84* «Бетонные и железобетонные конструкции», СНиП 52-01-2003, СНиП 2.03.11-85 «Защита строительных
конструкций от коррозии» и развивающими их документами.
2.
ОБЩИЕ ТРЕБОВАНИЯ К ЖЕЛЕЗОБЕТОННЫМ КОНСТРУКЦИЯМ С АРМАТУРОЙ КЛАССОВ
А500С И А400С
2.1 Для нормальной
эксплуатации в течение заданного срока службы зданий и сооружений
железобетонные конструкции с арматурой классов А500С и А400С должны
отвечать следующим требованиям:
—
безопасности (по несущей способности);
—
эксплуатационной пригодности;
—
долговечности.
Кроме того, конструкции
должны быть технологичными и экономичными.
2.2 Для обеспечения
безопасности железобетонные конструкции с арматурой классов А500С и
А400С должны иметь характеристики, с надлежащей степенью
надежности, предотвращающие возможность разрушения конструкций при
различных воздействиях.
2.3 Для выполнения
требования эксплуатационной пригодности железобетонные конструкции
с арматурой классов А500С и А400С должны иметь характеристики, при
которых с надлежащей степенью надежности под различными
воздействиями не происходило бы образование или чрезмерное
раскрытие трещин и не возникали чрезмерные деформации,
препятствующие нормальной эксплуатации (нарушение требований по
охране здоровья людей и окружающей среды; требований к внешнему
виду конструкции; технологических требований по нормальной работе
оборудования, механизмов; конструктивных требований по совместной
работе элементов и т.д.).
2.4* Для выполнения
требования долговечности железобетонные конструкции с арматурой
классов А500С и А400С должны иметь такие начальные характеристики,
чтобы с надлежащей степенью надежности в течение длительного
времени (заданного срока службы) конструкции отвечали бы
требованиям безопасности и эксплуатационной пригодности при
различных воздействиях.
Для железобетонных
конструкций, эксплуатируемых в агрессивных средах, следует
выполнять мероприятия по защите от коррозии в соответствии с
требованиями СНиП 2.03.11 и
МГСН 2.08-01.
2.5 Железобетонные
конструкции с арматурой классов А500С и А400С должны отвечать
требованиям технологичности при изготовлении, транспортировании и
монтаже.
2.6 Для выполнения
требований экономичности железобетонные конструкции с арматурой
классов А500С и А400С должны быть спроектированы, исходя из
оптимальных показателей по материалоемкости, энергоемкости,
трудоемкости и затрат при эксплуатации.
2.7 В соответствии с
положениями настоящих норм безопасность, эксплуатационная
пригодность, долговечность, технологичность и экономичность
железобетонных конструкций обеспечиваются выполнением
конструктивных, технологических и эксплуатационных требований.
Нагрузки и воздействия,
срок эксплуатации (службы) зданий и сооружений, предел
огнестойкости и способы защиты конструкций от коррозии
устанавливаются соответствующими нормативными документами.
2.8 При проектировании
железобетонных конструкций должны быть установлены вид и показатели
качества бетона и арматуры.
Арматура, используемая в
конструкциях, должна соответствовать проекту и иметь
соответствующие сертификаты и маркировку, подтверждающие ее
качество.
2.9 Расчеты
железобетонных конструкций необходимо выполнять с учетом возможного
образования трещин и неупругих деформаций в бетоне и арматуре.
Усилия и деформации от
различных воздействий в конструкциях и в образуемых ими системах
зданий и сооружений следует определять с учетом их совместной
работы, физической и геометрической нелинейности работы конструкций
в системе.
Расчеты железобетонных
конструкций для всех стадий их работы следует производить на
действие изгибающих моментов, продольных сил, поперечных сил и
крутящих моментов, возникающих в конструкциях при эксплуатации, а
также при изготовлении, транспортировании, возведении и местном
действии нагрузки.
Расчеты железобетонных
конструкций следует производить по методу предельных состояний,
включающему:
—
предельные состояния первой группы (по непригодности к эксплуатации
из-за потери несущей способности);
—
предельные состояния второй группы (по непригодности к нормальной
эксплуатации из-за образования или чрезмерного раскрытия трещин,
появления недопустимых деформаций и др.).
Расчеты по предельным
состояниям первой группы должны включать расчеты по прочности.
Расчеты по предельным
состояниям второй группы должны включать расчеты по образованию
трещин, по раскрытию трещин, по деформациям.
Расчеты должны
гарантированно предотвращать возможность достижения предельных
состояний конструкций.
В
необходимых случаях по соответствующим нормативным документам
следует производить расчеты по огнестойкости, теплопроводности,
звукоизоляции, обеспечивающие но