Расчетное сопротивление фанеры растяжению
При расчёте на прочность деревянных конструкций необходимо знать его расчётное сопротивление. Для деревянных конструкций есть несколько типов расчётных сопротивлений: на изгиб, сжатие, смятие, скол вдоль и поперёк волокон, растяжение вдоль и поперёк волокон, сжатие и смятие поперек волокон. Вначале рассмотрим, как вычисляется расчётное сопротивление деревянных конструкций, затем рассмотрим его расчёт на примере вычисления расчётного сопротивления на изгиб для доски балки перекрытия.
Методика расчёта взята из СП 64.133330.2017, который можно скачать по этой ссылке.
Расчётное сопротивление древесины определяем по формуле 1 СП
64.13330.2017:

где RA
– расчётное сопротивление древесины согласно таблицы 3 СП 64.13330.2017 в
зависимости от сечения и сорта древесины
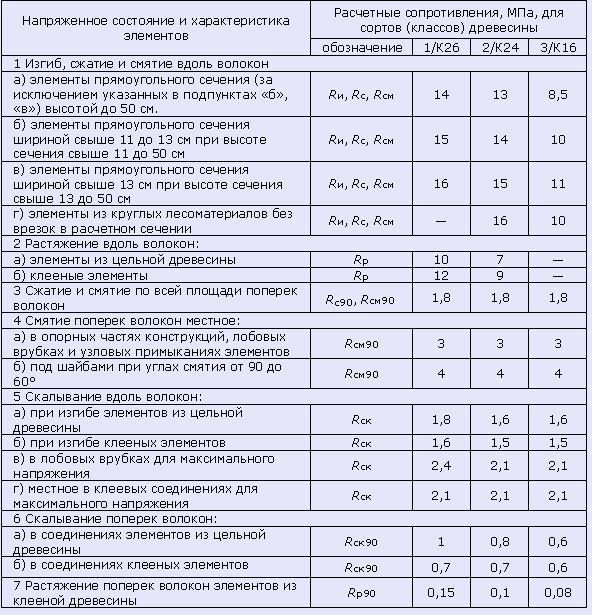
Таблица 3 СП 64.13330.2017:
| Напряженное состояние и характеристика элементов | Расчетное сопротивление, МПа, для сортов древесины | |||
|---|---|---|---|---|
| Обозначение | 1 | 2 | 3 | |
| 1 Изгиб, сжатие и смятие вдоль волокон: | ||||
| а) элементы прямоугольного сечения [за исключением указанных в б), в)] высотой не более 50 см. При высоте сечения более 50 см [см. 6.9в)] | 21 | 19,5 | 13 | |
| б) элементы прямоугольного сечения шириной от 11 до 13 см при высоте сечения от 11 до 50 см | 22,5 | 21 | 15 | |
| в) элементы прямоугольного сечения шириной более 13 см при высоте сечения от 13 до 50 см | 24 | 22,5 | 16,5 | |
| г) элементы из круглых лесоматериалов без врезок в расчетном сечении | — | 24 | 15 | |
| 2 Растяжение вдоль волокон: | ||||
| а) элементы из цельной древесины | 15 | 10,5 | — | |
| б) клееные элементы | 18 | 13,5 | — | |
| 3 Сжатие и смятие по всей площади поперек волокон | 2,7 | 2,7 | 2,7 | |
| 4 Смятие поперек волокон местное: | ||||
| а) в опорных частях конструкций, лобовых врубках и узловых примыканиях элементов | 4,5 | 4,5 | 4,5 | |
| б) под шайбами при углах смятия от 90° до 60° | 6 | 6 | 6 | |
| 5 Скалывание вдоль волокон: | ||||
| а) при изгибе элементов из цельной древесины | 2,7 | 2,4 | 2,4 | |
| б) при изгибе клееных элементов | 2,4 | 2,25 | 2,25 | |
| в) в лобовых врубках для максимального напряжения | 3,6 | 3,2 | 3,2 | |
| г) местное в клеевых соединениях для максимального напряжения | 3,2 | 3,2 | 3,2 | |
| 6 Скалывание поперек волокон в соединениях: | ||||
| а) элементов из цельной древесины | 1,5 | 1,2 | 0,9 | |
| б) клееных элементов | 1,05 | 1,05 | 0,9 | |
| 7 Растяжение поперек волокон элементов из клееной древесины | 0,23 | 0,15 | 0,12 | |
| 8 Срез под углом к волокнам 45° | 9 | 7,5 | 6 | |
| То же 90° | 16,5 | 13,5 | 12 | |
| Примечания: | ||||
| 1 В конструкциях построечного изготовления величины расчетных сопротивлений на растяжение, принятые по пункту 2а) настоящей таблицы, следует снижать на 30%. | ||||
| 2 Расчетное сопротивление изгибу для элементов настила и обрешетки под кровлю из древесины 3-го сорта следует принимать равным 13 МПа. | ||||
Расчетные сопротивления для
других пород древесины устанавливают путем умножения величин, приведенных в
таблице 3, на переходные коэффициенты mп, указанные
в таблице 5.
Таблица 5 СП 64.13330.2017
| Древесная порода | Коэффициент mп для расчетных сопротивлений | ||
|---|---|---|---|
| растяжению, изгибу, сжатию и смятию вдоль волокон RP , RИ , RС ,RСМ | сжатию и смятию поперек волокон RС90 , RСМ90 | скалыванию RСК | |
| Хвойные | |||
| 1 Лиственница, кроме европейской | 1,2 | 1,2 | 1 |
| 2 Кедр сибирский, кроме кедра Красноярского края | 0,9 | 0,9 | 0,9 |
| 3 Кедр Красноярского края | 0,65 | 0,65 | 0,65 |
| 4 Пихта | 0,8 | 0,8 | 0,8 |
| Твердые лиственные | |||
| 5 Дуб | 1,3 | 2 | 1,3 |
| 6 Ясень, клен, граб | 1,3 | 2 | 1,6 |
| 7 Акация | 1,5 | 2,2 | 1,8 |
| 8 Береза, бук | 1,1 | 1,6 | 1,3 |
| 9 Вяз, ильм | 1 | 1,6 | 1 |
| Мягкие лиственные | |||
| 10 Ольха, липа, осина, тополь | 0,8 | 1 | 0,8 |
| Примечание – Коэффициенты mп, указанные в таблице, для конструкций опор воздушных линий электропередачи, изготавливаемых из не пропитанной антисептиками лиственницы (при влажности 25%), умножаются на коэффициент 0,85. | |||
mДЛ – коэффициент
длительной прочности, принимаемый по таблице 4 СП 64.13330.2017 в зависимости и
того, для чего служит конструкция
Таблица 4 СП 64.13330.2017
| Обозначение режимов нагружения | Характеристика режимов нагружения | Приведенное расчетное время действия нагрузки, с | Коэффициент длительной прочности mДЛ |
| А | Линейно возрастающая нагрузка при стандартных машинных испытаниях | 1-10 | 1,0 |
| Б | Совместное действие постоянной и длительной временной нагрузок, напряжение от которых превышает 80% полного напряжения в элементах конструкций от всех нагрузок | 108-109 | 0,53 |
| В | Совместное действие постоянной и кратковременной снеговой нагрузок | 106-107 | 0,66 |
| Г | Совместное действие постоянной и кратковременной ветровой и (или) монтажной нагрузок | 103-104 | 0,8 |
| Д | Совместное действие постоянной и сейсмической нагрузок | 10-102 | 0,92 |
| Е | Действие импульсивных и ударных нагрузок | 10-1-10-8 | 1,1-1,35 |
| Ж | Совместное действие постоянной и кратковременной снеговой нагрузок в условиях пожара | 103-104 | 0,8 |
| И | Для опор воздушных линий электропередачи — гололедная, монтажная, ветровая при гололеде, от тяжения проводов при температуре ниже среднегодовой | 104-105 | 0,85 |
| К | Для опор воздушных линий электропередачи — при обрыве проводов и тросов | 10-1-10-2 | 1,1 |
Пmi
– произведение коэффициентов условий работ согласно п.6.9 СП 64.13330.2017.
Рассмотрим все коэффициенты:
п.6.9 а) для различных условий эксплуатации конструкций –
коэффициент mВ, указанный в таблице
9:
Таблица 9 СП 64.13330.2017
| Условие эксплуатации (таблица 1) | 1А и 1 | 2 | 3 | 4 |
| Коэффициент mВ | 1 | 0,9 | 0,85 | 0,75 |
Условия эксплуатации указаны в таблице 1 СП 64.13330.2017
Таблица 1 СП 64.13330.2017
| Класс условий эксплуатации | Эксплуатационная влажность древесины, % | Максимальная относительная влажность воздуха при температуре 20°С, % | |
| 1 (сухой) | 1а | Не более 8 | 40 |
| 1б | Не более 10 | 50 | |
| 2 (нормальный) | Не более 12 | 65 | |
| 3 (влажный) | Не более 15 | 75 | |
| 4 (мокрый) | 4а | Не более 20 | 85 |
| 4б | Более 20 | Более 85 | |
| Примечания 1 Допускается в качестве «эксплуатационной» принимать «равновесную» влажность древесины (рисунок А.1 Приложения А СП 64.13330.2017). 2 Допускается кратковременное превышение максимальной влажности в течение 2-3 нед. в году. | |||
п.6.9 б) конструкций,
эксплуатируемых при установившейся температуре воздуха ниже плюс 35°С, —
коэффициент mТ=1; при температуре
плюс 50°С – коэффициент mТ=0,8. Для промежуточных
значений температуры коэффициент принимают по интерполяции;
п.6.9 в) изгибаемых,
внецентренно сжатых, сжато-изгибаемых и сжатых клееных элементов прямоугольного
сечения высотой более 50 см значения расчетных сопротивлений изгибу и сжатию
вдоль волокон – коэффициент mб,
указанный в таблице 10:
Таблица 10 СП 64.13330.2017
| Высота сечения, см | 50 и менее | 60 | 70 | 80 | 100 | 120 и более |
| Коэффициент mб | 1 | 0,96 | 0,93 | 0,90 | 0,85 | 0,8 |
п.6.9 г) растянутых элементов с
ослаблением в расчетном сечении и изгибаемых элементов из круглых
лесоматериалов с подрезкой в расчетном сечении – коэффициент mо=0,8;
п.6.9 д) элементов, подвергнутых глубокой пропитке
антипиренами под давлением, — коэффициент mа=0,9;
п.6.9 е) изгибаемых,
внецентренно сжатых, сжато-изгибаемых и сжатых клееных деревянных элементов, в
зависимости от толщины слоев, значения расчетных сопротивлений изгибу,
скалыванию и сжатию вдоль волокон — коэффициент mСД,
указанный в таблице 11:
Таблица 11 СП 64.13330.2017
| Толщина слоя, мм | 10 и менее | 19 | 26 | 33 | 42 |
| Коэффициент mСД | 1,2 | 1,1 | 1,05 | 1,0 | 0,95 |
п.6.9 ж) гнутых элементов
конструкций значения расчетных сопротивлений растяжению, сжатию и изгибу —
коэффициент mГН, указанный в таблице
12:
Таблица 12 СП 64.13330.2017
| Напряженное состояние | Обозначение расчетных сопротивлений | Коэффициент mГН при отношении rK/a | |||
| 150 | 200 | 250 | 500 и более | ||
| Сжатие и изгиб | Rc, Rи | 0,8 | 0,9 | 1 | 1 |
| Растяжение | Rр | 0,6 | 0,7 | 0,8 | 1 |
| Примечание — rK — радиус кривизны гнутой доски или бруска; a — толщина гнутой доски или бруска в радиальном направлении. | |||||
п. 6.9 и) в зависимости от срока
службы – коэффициент mc.c, указанный в таблице 13:
Таблица 13 СП 64.13330.2017
| Вид напряженного состояния | Значение коэффициента mc.c при сроке службы сооружения | ||
| ≤50 лет | 75 лет | 100 лет и более | |
| Изгиб, сжатие, смятие вдоль и поперек волокон древесины | 1,0 | 0,9 | 0,8 |
| Растяжение и скалывание вдоль волокон древесины | 1,0 | 0,85 | 0,7 |
| Растяжение поперек волокон древесины | 1,0 | 0,8 | 0,5 |
| Примечание — Значение коэффициента mc.c для промежуточных сроков службы сооружения принимаются по линейной интерполяции. | |||
п. 6.9 к) для смятия поперек
волокон при режимах нагружения Г-К (таблица 4, приведена выше) — коэффициент mcм=1,15.
Пример расчёта
расчётного сопротивления
Для примера рассмотрим расчёт расчётного сопротивления на
изгиб для балки из доски сечением 50х200 из сосны 1-го сорта.
RAИ=21
МПа (п.1а таблицы 30)
mДЛ =0,53 (режим Б
таблицы 4)
mв=0,9 коэффициент для
условий эксплуатации подбирается по таблице 9 СП 64.13330.2017 согласно
условиям эксплуатации по таблице 1 СП 64.13330.2017. При влажности воздуха до
65% (для жилых помещений) данный коэффициент равен 0,9
mT =1– коэффициент
условий работы при температуре эксплуатации для температуры ниже +35°С равен
единице.
mб =1 коэффициент условий
работы в зависимости от высоты сечения при высоте сечения ниже 50 см равен 1.
mо – не применяется т.к.
наша конструкция не относится к ситуациям п.6.9 г.
mа— не применяется т.к.
доску мы не пропитываем антипиренами;
mСД – не применяется т.к.
данный коэффициент используется для клееных элементов;
mГН – не применяется т.к.
данный коэффициент используется для гнутых элементов;
mc.c =1
коэффициент условий работы для срока службы менее 50 лет. Срок службы здания
регламентирован ГОСТ 27751-2014 Надежность строительных конструкций и оснований
Таблица 1. Для здания и сооружений массового строительства в обычных условиях
эксплуатации (здания жилищно-гражданского и производственного строительства)
принимается не менее 50 лет.
mcм – не применяется т.к. в нашем
случае режим нагружения будет Б.
Итого Пmi
равен:
Пmi=
mв*mT*mб*mc.c =0,9*1*1*1=0,9
Вычисляем расчётное сопротивление изгибу:
Rи=RAИ *mДЛ*Пmi=21*0,53*0,9=10,017 МПа
Источник
При строительстве или ремонте деревянного дома использовать металлические, а тем более железобетонные балки перекрытия как-то не в тему. Если дом деревянный то и балки перекрытия логично сделать деревянными. Вот только на глаз не определишь, какой брус можно использовать для балок перекрытия и какой делать пролет между балками. Для ответа на эти вопросы нужно точно знать расстояние между опорными стенами и хотя бы приблизительно нагрузку на перекрытие.
Понятно, что расстояния между стенами бывают разные, да и нагрузка на перекрытие тоже может быть очень разная, одно дело расчет перекрытия, если сверху будет нежилой чердак и совсем другое дело расчет перекрытия для помещения, в котором будут в дальнейшем делаться перегородки, стоять чугунная ванна, бронзовый унитаз и много чего еще. Поэтому учесть все возможные варианты и выложить все в виде простой и понятной таблицы практически невозможно, а вот рассчитать сечение деревянной балки перекрытия и подобрать толщину досок, пользуясь приведенным ниже примером, я думаю, будет не очень сложно:
ПРИМЕР РАСЧЕТА ДЕРЕВЯННОЙ БАЛКИ ПЕРЕКРЫТИЯ
Помещения бывают разные, чаще не квадратные. Наиболее рационально крепить балки перекрытия так, чтобы длина балок была минимальной. Например если размер помещения 4х6 м, то если использовать балки длиной 4 метра, то требуемое сечение для таких балок будет меньше, чем для балок длиной 6 м. В данном случае размеры 4 м и 6 м условны, они означают длину пролета балок а не длину самих балок. Балки, само собой, будут длинее на 30-60 см.
Теперь попробуем определиться с нагрузкой. Обычно перекрытия жилых зданий рассчитываются на распределенную нагрузку 400 кг/м². Считается, что для большинства расчетов такой нагрузки достаточно, а для расчета чердачного перекрытия хватит даже 200 кг/м². Поэтому дальнейший расчет будет проводиться для вышеуказанной нагрузки при расстоянии между стенами 4 метра.
Деревянную балку перекрытия можно рассматривать как балку на двух шарнирных опорах, в этом случае расчетная модель балки будет выглядеть так:
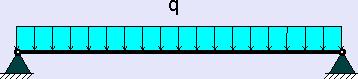
1. Вариант.
Если расстояние между балками будет 1 метр, то максимальный изгибающий момент:
Мmax = (q х l²) / 8 = 400х4²/8 = 800 кг·м или 80.000 кг·см
Теперь легко определить требуемый момент сопротивления деревянной балки
Wтреб = Мmax / R
где R — расчетное сопротивление древесины. В данном случае балка на двух шарнирных опорах работает на изгиб. Значение расчетного сопротивления можно определить по следующей таблице:
Значения расчетных сопротивлений для сосны, ели и лиственницы при влажности 12%
согласно СНиП II-25-80 (СП 64.13330.2011)

А если материал балки не сосна, то следует расчетное значение умножить на переходный коэффициент согласно следующей таблицы:
Переходные коэффициенты для других пород древесины
согласно СНиП II-25-80 (СП 64.13330.2011)
| Древесные породы | Коэффициент mn для расчетных сопротивлений | ||
| растяжению, изгибу, сжатию и смятию вдоль волокон Rp, Rи, Rс, Rсм | сжатию и смятию поперек волокон Rс90, Rсм90 | скалыванию Rск | |
| Хвойные | |||
| 1. Лиственница, кроме европейской | 1,2 | 1,2 | 1,0 |
| 2. Кедр сибирский, кроме кедра Красноярского края | 0,9 | 0,9 | 0,9 |
| 3. Кедр Красноярского края | 0,65 | 0,65 | 0,65 |
| 4. Пихта | 0,8 | 0,8 | 0,8 |
| Твердые лиственные | |||
| 5. Дуб | 1,3 | 2,0 | 1,3 |
| 6. Ясень, клен, граб | 1,3 | 2,0 | 1,6 |
| 7. Акация | 1,5 | 2,2 | 1,8 |
| 8. Береза, бук | 1,1 | 1,6 | 1,3 |
| 9. Вяз, ильм | 1,0 | 1,6 | 1,0 |
| Мягкие лиственные | |||
| 10. Ольха, липа, осина, тополь | 0,8 | 1,0 | 0,8 |
| Примечание: коэффициенты mn, указанные в таблице, для конструкций опор воздушных линий электропередачи, изготавливаемых из не пропитанной антисептиками лиственницы (при влажности ≤25%), умножаются на коэффициент 0,85. | |||
Для конструкций, в которых напряжения, возникающие от постоянных и временных длительных нагрузок, превышают 80 % суммарного напряжения от всех нагрузок, расчетное сопротивление следует дополнительно умножить на коэффициент mд = 0,8. (п.5.2.в СП 64.13330.2011)
А если Вы планируете срок службы Вашей конструкции более 50 лет, то полученное значение расчетного сопротивления следует умножить еще на один коэффициент, согласно следующей таблицы:
Коэффициенты срока службы для древесины
согласно СНиП II-25-80 (СП 64.13330.2011)
| Срок службы сооружения | до 50 лет | 50-100 лет | более 100 лет |
| Коэффициент надежности по сроку службы γн(cc) | 1,0 | 0,9 | 0,8 |
Таким образом расчетное сопротивление балки может снизиться почти в два раза и соответственно сечение балки увеличится, но мы пока никаких дополнительных коэффициентов использовать не будем. Если будет использоваться древесина сосна 1 сорта, то
Wтреб = 80000 / 142,71 = 560,57 см³
Примечание: Расчетное сопротивление 14 МПа = 142,71 кгс/см². Впрочем для упрощения расчетов можно использовать и значение 140 большой ошибки в этом не будет, а будет небольшой запас по прочности.
Так как поперечное сечение бруса имеет простую прямоугольную форму, то момент сопротивления бруса определяется по формуле
Wтреб = b x h² / 6
где b — ширина бруса, h — высота бруса. Если поперечное сечение балки перекрытия будет непрямоугольным, а, например, круглым, овальным и др, т.е. в качестве балок Вы будете использовать лес-кругляк, тесаные бревна или что-то еще, то определить момент сопротивления для таких сечений можно по формулам, приведенным отдельно.
Попробуем определить необходимую высоту бруса при ширине 10 см. В этом случае
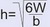
высота бруса должна быть не менее 18,34 см. т.е. можно использовать брус сечением 10х20 см. В этом случае потребуется 0,56 м³ древесины на 7 балок перекрытия.
Для примера, если Вы планируете, что ваша конструкция простоит более 100 лет и при этом более 80% нагрузки будет постоянная + длительная, то расчетное сопротивление для древесины того же класса составит 91,33 кгс/см² и тогда требуемый момент сопротивления увеличится до 876 см³ и высота бруса при этом должна быть не менее 22,92 см.
2 Вариант.
Если расстояние между балками сделать 75 см, то максимальный изгибающий момент:
Мmax = (q х l²) / 8 = (400 х 0,75
х 4²) / 8 = 600 кг·м или 60000 кг·см
тогда требуемый момент сопротивления деревянной балки
Wтреб = 60000 / 142,71 = 420,43 см³
а минимально допустимая высота бруса 15,88 см при ширине бруса 10 см, если использовать брус сечением 10х17,5 см, то на 9 балок перекрытия потребуется 0,63 м³ древесины.
3 Вариант.
Если расстояние между балками сделать 50 см, то максимальный изгибающий момент:
Мmax = (q х l²) / 8 = (400 х 0,5 х 4²) / 8 = 400 кг·м или 40000 кг·см
тогда требуемый момент сопротивления деревянной балки
Wтреб = 40000 / 100 = 280,3 см³
а минимально допустимая высота бруса 12,96 см при ширине балки 10 см, при использовании бруса сечением 10х15 см на 13 балок перекрытия потребуется 0,78 м³ древесины.
Как видно из расчетов, чем меньше расстояние между балками, тем больше может быть расход древесины на балки, но при этом чем меньше расстояние между балками, тем более тонкие доски или листовой материал можно использовать для настилки пола. И еще один важный момент — расчетное сопротивление древесины зависит от породы древесины и влажности древесины. Чем выше влажность, тем меньше расчетное сопротивление. В зависимости от породы древесины колебания расчетного сопротивления не очень большие.
Теперь проверим прогиб балки, рассчитанной по первому варианту. Большинство справочников предлагают определять величину прогиба при распределенной нагрузке и шарнирном опирании балки по следующей формуле:
f=(5ql4)/(384EI)
где,
q — нагрузка на балку;
l — расстояние между несущими стенами;
E — модуль упругости. Для древесины не взирая на породы согласно п.5.3 СП 64.13330.2011; при расчете по предельным состояниям второй группы это значение обычно принимается равным 10000 МПа или 10х108 кгс/м² (10х104 кгс/см²) вдоль волокон и Е90 = 400 МПа поперек волокон. Но в действительности значение модуля упругости даже для сосны еще колеблется от 7х108 до 11х108 кгс/м², в зависимости от влажности древесины и времени действия нагрузки. При длительном действии нагрузки, согласно п.5.4 СП 64.13330.201, при расчете по предельным состояниям первой группы по деформированной схеме нужно использовать коэффициент mдс = 0,75. Мы не будем определять прогиб для случая, когда временная нагрузка на балку длительная, балки перед установкой не обрабатываются глубокой пропиткой, препятствующей изменению влажности древесины и относительная влажность древесины может превысить 20%, в этом случае модуль упругости будет около 6х108 кгс/м², но значение это запомним.
I — момент инерции, для доски прямоугольного сечения.
I = (b x h³) / 12 = 10 х 20³ / 12 = 6666,67 см4
f = (5 х 400 х 44) / (384 х 10 х 108 х 6666,67 х 10-8) = 0,01999 м или 2,0 см.
СНиП II-25-80 (СП 64.13330.2011) рекомендует рассчитывать деревянные конструкции так, чтобы для балок перекрытия прогиб не превышал 1/250 от длины пролета, т.е. допустимый максимальный прогиб 400/250=1,6 см. Это условие нами не выполнено. Далее следует подобрать такое сечение балки, прогиб которой устраивает или Вас или СНиП.
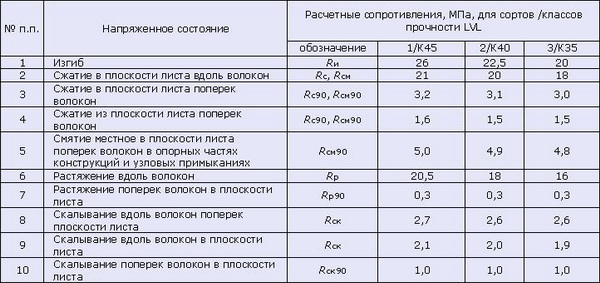
Если для балок перекрытия Вы будете использовать клееный брус LVL (Laminated Veneer Lumber), то расчетные сопротивления для такого бруса следует определять по следующей таблице:
Значения расчетных сопротивлений для клееных слоистых материалов
согласно СНиП II-25-80 (СП 64.13330.2011)
Расчет на смятие опорных участков балки как правило не требуется. А вот расчет на прочность при действии касательных напряжений сделать не сложно и здесь. Максимальные касательные напряжения при выбранной расчетной схеме будут в поперечных сечениях на опорах балки, там, где изгибающий момент равен нулю. В этих сечениях значение поперечной силы будет равно опорной реакции и будет составлять:
Q = ql/2 = 400 x 4 / 2 = 800 кг
тогда значение максимальных касательных напряжений составит:
т = 1,5Q/F = 1,5 x 800 / 200 = 6 кг/см² < Rcк = 18 кг/см²,
где,
F — площадь поперечного сечения бруса сечением 10х20 см;
Rcк — расчетное сопротивление скалыванию вдоль волокон, определяется по первой таблице.
Как видим, имеется трехкатный запас по прочности даже для бруса, имеющего максимальную высоту сечения.
Теперь рассчитаем какие доски выдержат расчетную нагрузку (принцип расчета точно такой же).
ПРИМЕР РАСЧЕТА НАПОЛЬНОГО ПОКРЫТИЯ
1 Вариант. Напольное покрытие из половых досок.
При расстоянии между балками 1 м максимальный изгибающий момент:
Мmax = (q х l²) / 8 = (400 х 1²) / 8 = 50 кг·м или 5000 кг·см
В данном случае расчетная схема для досок, как для однопролетной балки на шарнирных опорах принята весьма условно. Более правильно половые доски длиной от стены до стены, рассматривать, как многопролетную неразрезную балку. Однако в этом случае придется учитывать и количество пролетов и способ крепления досок к лагам. Если же на некоторых участках будут уложены доски между двумя лагами, то такие доски действительно следует рассматривать как однопролетные балки и для таких досок изгибающий момент будет максимальным. Именно это вариант мы и будем далее рассматривать. Требуемый момент сопротивления досок
Wтреб = 5000 / 130 = 38,46 см³
так как нагрузка у нас распределена по всему расчетному участку, то напольное покрытие из досок можно условно рассматривать как одну доску шириной 100 см, тогда минимально допустимая высота досок 1,52 см, при меньших пролетах требуемая высота доски будет еще меньше. Это означает что настилать пол можно стандартными половыми досками высотой 30-35 мм.
Но вместо дорогих половых досок можно использовать более дешевые листовые материалы, например, фанеру, ДСП, OSB.
2 Вариант. Напольное покрытие из фанеры.
Расчетное сопротивление фанеры можно определить по следующей таблице:
Значения расчетных сопротивлений для фанеры
согласно СНиП II-25-80 (СП 64.13330.2011)
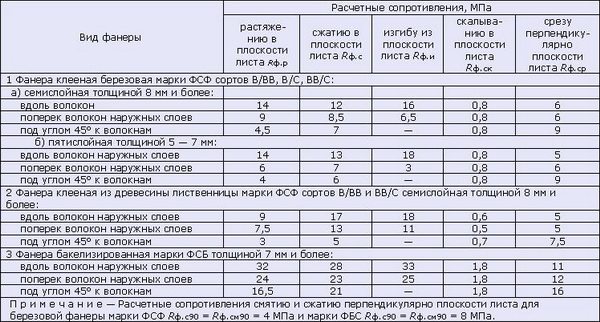
Так как фанера изготовлена из склеенных слоев древесины, то и расчетное сопротивление фанеры должно быть близким к расчетному сопротивлению древесины, но так как слои чередуются — один слой вдоль волокон, второй поперек, то общее расчетное сопротивление можно принимать как среднее арифметическое. Например для березовой фанеры марки ФСФ
Rф = (160 + 65) / 2 = 112,5 кгс/м²
тогда требуемый момент сопротивления фанеры
Wтреб = 5000 / 112,5 = 44,44 см³
минимально допустимая толщина фанеры 1,63 см, т.е на балки можно укладывать фанеру толщиной 18 мм и более при расстоянии между балками 1 м.
При расстоянии между балками 0,75 м значение изгибающего момента уменьшится
Мmax = (q х l²) / 8 = (400 х 0,75²) / 8 = 28,125 кг·м или 2812,5 кг·см
требуемый момент сопротивления фанеры
Wтреб = 2812,5 / 112,5 = 25 см³
минимально допустимая толщина фанеры 1,22 см, т.е на балки можно укладывать фанеру толщиной 14 мм и более при расстоянии между балками 0,75 м.
При расстоянии между балками 0,5 м изгибающий момент составит
Мmax = (q х l²) / 8 = (400 х 0,5²) / 8 = 12,5 кг·м или 1250 кг·см
требуемый момент сопротивления фанеры
Wтреб = 1250 / 112,5 = 11,1 см³
минимально допустимая толщина фанеры 0,82 см, т.е на балки можно укладывать фанеру толщиной 9,5 мм и более при расстоянии между балками 0,5 м. Однако, если рассчитать прогиб фанеры (подробно расчет не приводится), то прогиб составит около 6,5 мм, а это в 3 раза больше допустимого прогиба. При толщине фанеры 14 мм прогиб составит около 2,3 мм, что практически удовлетворяет требованиям СНиПа.
Общее примечание: вообще-то при расчете деревянных конструкций применяется куча всяких поправочных коэффициентов, но мы решили не усложнять приведенный расчет коэффициентами, достаточно того, что мы взяли максимально возможную нагрузку и кроме того при подборе сечения есть неплохой запас.
3 Вариант. Напольное покрытие из ДСП или OSB.
Вообще-то использовать ДСП или OSB в качестве напольного покрытия (пусть даже и чернового) по балкам перекрытия нежелательно, да и не предназначены эти листовые материалы для этого, слишком много у них недостатков. Расчетное сопротивление прессованных листовых материалов зависит от слишком большого количества факторов, поэтому какое значение расчетного сопротивления можно использовать при расчетах, Вам никто не скажет.
Тем не менее запретить использовать ДСП или OSB мы не можем, только добавим: толщина ДСП или OSB должна быть в 1,5-2 раза больше чем для фанеры. Полы с провалившимся ДСП приходилось ремонтировать неоднократно, да и сосед недавно выравнивавший деревянный пол плитами OSB, тоже жалуется на провалы, так что можете поверить на слово.
Примечание: на балки перекрытия могут сначала опираться лаги, а потом к лагам будут крепиться доски. В этом случае необходимо рассчитать дополнительно сечение лаг по вышеприведенному принципу.
Источник
