Расчет прямоугольного сечения на растяжение

где N — продольная растягивающая сила, действующая на стержень;
F — площадь поперечного сечения стержня;
σ — нормальные напряжения, возникающие в рассматриваемом поперечном сечении стержня в ответ на действие растягивающей продольной силы;
Rр — расчетное сопротивление материала стержня растяжению (для некоторых материалов расчетные сопротивления растяжению, сжатию, изгибу и т.п. могут различаться).
Визуально это может выглядеть так:

Рисунок 525.1. Нормальные напряжения при растяжении прямолинейного стержня.
На рисунке 525.1.а) мы видим прямолинейный стержень длиной l, показанный серым цветом, к которому приложена растягивающая сила N. При этом точка приложения силы находится на нейтральной оси стержня, совпадающей с осью х, показанной пунктирной линией.
Для упрощения расчетов заменяем опору А соответствующей опорной реакцией А (рис.525.1.б). Исходя из условий статического равновесия:
∑х = А + N = 0 (149.5.2)
А = — N (525.2)
Это означает, что опорная реакция A равна по значению растягивающей силе N, но направлена в противоположную сторону.
Если взглянуть на эту ситуацию под некоторым углом, то она будет выглядеть так, как показано на рисунке 525.1.в). На этом рисунке мы видим, что нормальные напряжения — это реакция материала на действие растягивающей силы и направлены эти напряжения в сторону, противоположную действию сил. Другими словами нормальные напряжения препятствуют деформации растяжения, и направлены на то, чтобы вернуть материалу исходную форму. Иногда для упрощения восприятия нормальные напряжения, возникающие при растяжении, принято изображать направленными от сечения, как показано на рисунке 525.1.г), а сжимающие напряжения — направленными к сечению. С точки зрения физики такая замена вполне допустима, так как нормальные напряжения (внутренние силы) можно рассматривать как плоскую нагрузку, распределенную по всей площади сечения (внешнюю силу). Как правило растягивающие нормальные напряжения рассматриваются как положительные, а сжимающие — как отрицательные.
Сечение стержня, показанное на рисунке 525.1.в) розовым цветом, является перпендикулярным нейтральной оси стержня и называется поперечным сечением.
Как следует из формулы (525.1) и из приведенного рисунка, длина стержня l на значение нормальных напряжений никак не влияет. А вот параметры поперечного сечения стержня: ширина сечения b и высота сечения h, если сечение прямоугольное, очень даже влияют, так как от этих параметров зависит площадь F поперечного сечения.
Примечание: конечно же поперечное сечение стержня далеко не всегда имеет прямоугольную форму, как показано на рисунке 525.1.в). Поперечное сечение может быть и круглым, и овальным, и ромбическим, и вообще иметь любую сколь угодно сложную форму, тем не менее форма поперечного сечения никак на значение нормальных напряжений не влияет (во всяком случае такое допущение принимается в теории сопротивления материалов), а влияет только площадь сечения, определить которую тем сложнее, чем более сложной является форма поперечного сечения.
Проверить данные постулаты теории сопротивления материалов очень легко и просто. Достаточно взять нитку и попробовать ее разорвать (вариант а)). Затем разорвать нитки с с той же катушки, но б) более короткую и в) более длинную, чем в первом случае. Во всех трех случаях усилие, которое необходимо приложить для разрыва нитки, будет примерно одинаковым.
Но если одну из ниток сложить вдвое и попробовать разорвать, то усилие, необходимое для разрыва нитки, увеличится в 2 раза. Все потому, что условная площадь сечения стержня, работающего на растяжение, увеличится при складывании нитки в 2 раза.
Таким образом известная пословица: «где тонко, там и рвется» в переводе на язык теории сопротивления материалов будет звучать примерно так: «при действии растягивающих нормальных напряжений разрушение материала, обладающего постоянным сопротивлением растяжению по всей длине, будет происходить в сечении с минимальной площадью». Это особенно актуально для стержней с изменяющейся по длине площадью сечения.
С учетом различных факторов формула (525.1) может иметь другой вид:
Nγn/Fn = σ ≤ Rрγs (512.1.2)
где γn — коэффициент надежности по нагрузке (как правило больше единицы), Fn — минимальная площадь сечения (с учетом возможных ослаблений отверстиями, пазами и т.п.), γs — коэффициент условий работы (как правило меньше единицы).
Т.е. теория сопротивления материалов допускает, что нормальные напряжения в стержне могут быть равны расчетному сопротивлению материала на растяжение, умноженному на коэффициент условий работы.
Пример расчета стержня на растяжение
Дано: На стальной стержень (см. рис.525.1.а)) с расчетным сопротивлением Rp = 2250 кг/см2 действует продольная растягивающая сила N = 30 тонн. Коэффициент надежности по нагрузке γn = 1.05, коэффициент условий работы γs = 0.9. Собственным весом стержня в виду его незначительности по сравнению с действующей нагрузкой для упрощения расчетов можно пренебречь. Предполагается, что нагрузка прикладывается по всей площади поперечного сечения стержня, т.е. возникающие нормальные напряжения будут равномерно распределенными по всей площади сечения.
Требуется: Подобрать диаметр стержня.
Решение:
1. Определяем требуемую площадь сечения стержня, преобразовав формулу (525.1.2)
F = Nγn/Rpγs = 30000·1.05/(2250·0.9) = 15.56 см2.
2. Определяем диаметр стержня
d = √4F/п = √4·15.56/3.14 = 4.45 см
Как видим сам расчет занимает гораздо меньше времени, чем описание физических характеристик используемых данных и даже формулировка условия задачи.
Источник
Круглое сечение.
Кольцевое сечение.
Расчет балок на прочность.
Расчет по допускаемым напряжениям на прочность при изгибе.
| – при симметричном сечении |
Проверка прочности по предельным состояниям.
– максимальный изгибающий момент от расчетных нагрузок.
Рр=Рн×n
n – коэффициент перегрузки.
– нормативная нагрузка.
Рр – расчетная нагрузка.
– коэффициент условия работы.
Если материал работает неодинаково на растяжение и сжатие, то прочность проверяется по формулам:
где Rp и Rсж – расчетное сопротивление на растяжение и сжатие
Расчет по несущей способности и учетом пластической деформации.
В предыдущих методах расчета прочность проверяется по максимальны напряжениям в верхних и нижних волокнах балки. При этом средние волокна оказываются недогруженными.
Оказывается, если нагрузку увеличивать дальше, то в крайних волокнах напряжение дойдет до предела текучести σт ( в пластичных материалах), и до предела прочности σnч ( в хрупких материалах). При дальнейшем увеличении нагрузки хрупкие материалы разрушатся, а в пластичных материалах напряжения в крайних волокнах далее не возрастают, а растут во внутренних волокнах. (см. рис.)
Несущая способность балки исчерпывается, когда по всему сечению напряжения достигнут σт.
Для прямоугольного сечения:
Примечание: для прокатных профилей (швеллер и двутавр) пластический момент Wnл=(1.1÷1,17)×W
Касательные напряжения при изгибе балки прямоугольного сечения. Формула Журавcкого.
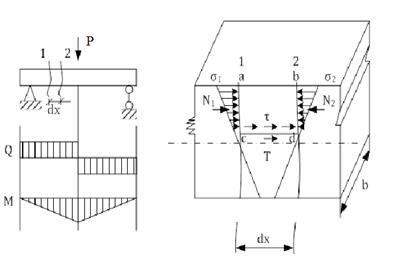
Так как момент в сечении 2 больше момента в сечении 1, то напряжение σ2>σ1=>N2>N1.
В этом случае элемент abcd должен переместиться влево. Этому перемещению препятствуют касательные напряжения τ на площадке cd.
— уравнение равновесия, после преобразования которого получается формула для определения τ: — Формула Журавского
| где Q — поперечная сила, Sотс — статический момент отсеченной части относительно нейтральной оси, J-момент инерции всего сечения относительно нейтральной оси, b — ширина балки на уровне y. |
Распределение касательных напряжений в балках прямоугольного, круглого и двутаврового сечений.
1. Прямоугольное сечение:
2.Круглое сечение.
3. Двутавровое сечение.
Главные напряжения при изгибе. Проверка прочности балок.
| Выделим из балки участок, на который действует максимально поперечная сила Qmax и изгибающий момент Mmax. Наиболее опасными точками являются сечение A и точка Б. Прочность проверяется по напряжениям в этих точках. На практике обычно ограничиваются проверкой сечения A: |
[σсж]
Примечание: при расчете по предельным состояниям вместо [σсж] и [σр] в формулы ставятся Rcж и Rp – расчетные сопротивления материала при сжатии и растяжении.
Если же балка короткая, то проверяют точку Б:
где Rсрез – расчетное сопротивление материала на срез.
В точке D на элемент действует нормальные и касательные напряжения, поэтому в некоторых случаях их совместное действие вызывает опасность для прочности. В этом случае элемент D проверяют на прочность используя главные напряжения.
В нашем случае: , следовательно:
Используя σ 1 и σ2 по теории прочности проверяют элемент D.
По теории наибольших касательных напряжений имеем: σ 1 — σ2≤R
Примечание: точку D следует брать по длине балки там, где одновременно действуют большие M и Q.
По высоте балки выбираем такое место, где одновременно действуют значения σ и τ.
Из эпюр видно:
1. В балках прямоугольного и круглого сечения отсутствуют точки, в которых одновременно действуют большие σ и τ. Поэтому в таких балках проверка точки D не делается.
2. В балках двутаврового сечения на границе пересечения полки со стенкой (т. А) одновременно действуют большие σ и τ. Поэтому они проверяются на прочность в этой точке.
Примечание:
a) В прокатных двутаврах и швеллерах в зоне пересечения полки со стенкой сделаны плавные переходы (закругления). Стенка и полка подобраны так, что точка A оказывается в благоприятных условиях работы и проверка прочности не требуется.
b) В составных (сварных) двутавровых балках проверка точки А необходима.
Источник



2.4. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ РАСТЯЖЕНИИ Основной задачей расчета конструкции на растяжение является обеспечение ее прочности в условиях эксплуатации. Условие прочности – оценка прочности элемента конструкции, сводящаяся к сравнению расчетных напряжений с допускаемыми: σ≤рσ[р ]; σ с ≤[ с],σ (2.9) где σр и σс – наибольшие расчетные растягивающие и сжимающие напряжения; [σр] и [σс] – допускаемые напряжения при растяжении и сжатии. Допускаемое напряжение – наибольшее напряжение, которое можно допустить в элементе конструкции при условии его безопасной, долговечной и надежной работы: Здесь σпред – предельное напряжение (состояние), при котором конструкция перестает удовлетворять эксплуатационным требованиям; им мо- гут быть предел текучести, предел прочности, предел выносливости, пре- дел ползучести и др. Для конструкций из пластичных материалов при определении допускаемых напряжений используют предел текучести σт (рис. 2.4, а). Это связано с тем, что в случае его превышения деформации резко возрастают при незначительном увеличении нагрузки и конструкция перестает удовлетворять условиям эксплуатации. Допускаемое напряжение в этом случае определяют как Для хрупких материалов (чугун, бетон, керамика) где σвр и σвс – пределы прочности при растяжении и сжатии (рис. 2.4, б). Здесь [n] – нормативный коэффициент запаса прочности. В зависимости от той предельной характеристики, с которой сравнивают расчетное напряжение σ, различают [nт] – нормативный коэффициент запаса прочности по отношению к пределу текучести σт и [nв] – нормативный коэффициент запаса прочности по отношению к пределу прочности σв. Запас прочности – отношение предельно допустимой теоретической нагрузки к той нагрузке, при которой возможна безопасная работа конструкции с учетом случайных перегрузок, непредвиденных дефектов и недостоверности исходных данных для теоретических расчетов. Нормативные коэффициенты запаса прочности зависят: − от класса конструкции (капитальная, временная), − намечаемого срока эксплуатации, − условий эксплуатации (радиация, коррозия, загнивание), − вида нагружения (статическое, циклическое, ударные нагрузки) − неточности задания величины внешних нагрузок, − неточности расчетных схем и приближенности методов расчета − и других факторов. Нормативный коэффициент запаса прочности не может быть единым на все случаи жизни. В каждой отрасли машиностроения сложились свои подходы, методы проектирования и приемы технологии. В изделиях общего машиностроения принимают [nт] = 1,3 – 2,2; [nв] = 3 – 5. Вероятность выхода из строя приближенно можно оценить с помощью коэффициента запаса в условии прочности: n = 1 соответствует вероятности невыхода из строя 50 %; n = 1,2 соответствует вероятности невыхода из строя 90 %; n = 1,5 соответствует вероятности невыхода из строя 99 %; n = 2 соответствует вероятности невыхода из строя 99,9 %. Для неответственных деталей n = 2 много. Для ответственных – мало. Так для каната подъемного лифта это означает на 1000 подъемов одно падение. При расчете конструкций на прочность встречаются три вида задач, которые вытекают из условия прочности а) поверочный расчет (проверка прочности). Известны усилие N и площадь A. Вычисляют σ = N/A и, сравнивая его с предельным σт или σв (для пластичного и хрупкого материалов соответственно), находят фактический коэффициент запаса прочности который затем сопоставляют с нормативным [n]; б) проектный расчет (подбор сечения). Известны внутреннее усилие N и допускаемое напряжение [σ]. Определяют требуемую площадь поперечного сечения стержня в) определение грузоподъемности (несущей способности). Известны площадь А и допускаемое напряжение [σ]. Вычисляют внутреннее усилие N≤N[ ] = ⋅[σ]A, (2.15) а затем в соответствие со схемой нагружения – величину внешней нагрузки F ≤ [F].
Источник
Эта статья будет посвящена расчетам на прочность, которые выполняются в сопромате и не только. Расчеты на прочность бывают двух видов: проверочные и проектировочные (проектные).
Проверочные расчеты на прочность – это такие расчеты, в ходе которых проверятся прочность элемента заданной формы и размеров, под некоторой нагрузкой.
В ходе проектировочных расчетов на прочность определяются какие-то размеры элемента из условия прочности. Причем, очевидно, что для разных видов деформаций эти условия прочности различны. Также к проектным расчетам можно отнести расчеты на грузоподъемность, когда вычисляется максимальная нагрузка, которую может выдерживать конструкция, не разрушаясь. Рассмотрим более подробно, как проводится прочностные расчеты для разных случаев.
Расчеты на прочность при растяжении (сжатии)
Начнем, пожалуй, с самого простого вида деформации растяжения (сжатия). Напряжение при центральном растяжении (сжатии) можно получить, разделив продольную силу на площадь поперечного сечения, а условие прочности выглядит вот так:

где сигма в квадратных скобках – это допустимое напряжение. Которое можно получить, разделив предельное напряжения на коэффициент запаса прочности:

Причем, за предельное напряжение для разных материалов принимают разное значение. Для пластичных материалов, например, для малоуглеродистой стали (Ст2, Ст3) принимают предел текучести, а для хрупких (бетон, чугун) берут в качестве предельного напряжения – предел прочности (временное сопротивление). Эти характеристики получают при испытании образцов на растяжение или сжатие на специальных машинах, которые фиксируют характеристики в виде диаграммы.

Коэффициент запаса прочности выбирается конструктором исходя из своего личного опыта, назначения проектируемой детали и сферы применения. Обычно, он варьируется от 2 до 6.
В случае если необходимо подобрать размеры сечения, площадь выражают таким образом:

Таким образом, минимальная площадь поперечного сечения при центральном растяжении (сжатии) будет равна отношению продольно силы к допустимому напряжению.
Расчеты на прочность при кручении
При кручении расчеты на прочность в принципе схожи с теми, что проводятся при растяжении. Только здесь вместо нормальных напряжений появляются касательные напряжения.
На кручение работают, чаще всего, детали, которые называются валами. Их назначение заключается в передаче крутящего момента от одного элемента к другому. При этом вал по всей длине имеет круглое поперечное сечение. Условие прочности для круглого поперечного сечения можно записать так:

где Ip — полярный момент сопротивления, ρ — радиус круга. Причем по этой формуле можно определить касательное напряжение в любой точке сечения, варьируя значение ρ. Касательные напряжения распределены неравномерно по сечению, их максимальное значение находится в наиболее удаленных точках сечения:

Условие прочности, можно записать несколько проще, используя такую геометрическую характеристику как момент сопротивления:

То бишь максимальные касательные напряжения равны отношению крутящего момента к полярному моменту сопротивления и должны быть меньше либо равны допустимому напряжению. Геометрические характеристики для круга, упомянутые выше можно найти вот так:

Иногда в задачах встречаются и прямоугольные сечения, для которых момент сопротивления определяется несколько сложнее, но об этом я расскажу в другой статье.
Расчеты на прочность при изгибе
Источник
Внутренние усилия при растяжении-сжатии.
Осевое (центральное) растяжение или сжатие прямого бруса вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса. При растяжении или сжатии в поперечных сечениях бруса возникают только продольные силы N. Продольная сила N в некотором сечении равна алгебраической сумме проекции на ось стержня всех внешних сил, действующих по одну сторону от рассматриваемого сечения. По правилу знаков продольной силы N принято считать, что от растягивающих внешних нагрузок возникают положительные продольные силы N, а от сжимающих — продольные силы N отрицательны (рис. 5).

Чтобы выявить участки стержня или его сечения, где продольная сила имеет наибольшее значение, строят эпюру продольных сил, применяя метод сечений, подробно рассмотренный в статье:
Анализ внутренних силовых факторов в статистически определимых системах
Ещё настоятельно рекомендую взглянуть на статью:
Расчёт статистически определимого бруса
Если разберёте теорию в данной статье и задачи по ссылкам, то станете гуру в теме «Растяжение-сжатие» =)
Напряжения при растяжении-сжатии.
Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:
где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.
Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:
Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.
Деформации при растяжении-сжатии.
Рассмотрим деформации, возникающие при растяжении (сжатии) стержня (рис.6, а). Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l1 и его длины до деформации l
Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением, или относительной продольной деформацией:
При растяжении продольная деформация положительна, а при сжатии – отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:
где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).
Таблица 1
Модуль продольной упругости для различных материалов

Абсолютная поперечная деформация бруса равна разности размеров поперечного сечения после и до деформации:
Соответственно, относительную поперечную деформацию определяют по формуле:
При растяжении размеры поперечного сечения бруса уменьшаются, и ε’ имеет отрицательное значение. Опытом установлено, что в пределах действия закона Гука при растяжении бруса поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε’ к продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона μ:
Экспериментально установлено, что на упругой стадии нагружения любого материала значение μ = const и для различных материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5 (табл. 2).
Таблица 2
Коэффициент Пуассона.

Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N:
Данной формулой можно пользоваться для вычисления абсолютного удлинения участка стержня длиной l при условии, что в пределах этого участка значение продольной силы постоянно. В случае, когда продольная сила N изменяется в пределах участка стержня, Δl определяют интегрированием в пределах этого участка:
Произведение (Е·А) называют жесткостью сечения стержня при растяжении (сжатии).
Механические свойства материалов.
Основными механическими свойствами материалов при их деформации являются прочность, пластичность, хрупкость, упругость и твердость.
Прочность — способность материала сопротивляться воздействию внешних сил, не разрушаясь и без появления остаточных деформаций.
Пластичность – свойство материала выдерживать без разрушения большие остаточные деформации. Неисчезающие после снятия внешних нагрузок деформации называются пластическими.
Хрупкость – свойство материала разрушаться при очень малых остаточных деформациях (например, чугун, бетон, стекло).
Идеальная упругость – свойство материала (тела) полностью восстанавливать свою форму и размеры после устранения причин, вызвавших деформацию.
Твердость – свойство материала сопротивляться проникновению в него других тел.
Рассмотрим диаграмму растяжения стержня из малоуглеродистой стали. Пусть круглый стержень длинной l0 и начальным постоянным поперечным сечением площади A0 статически растягивается с обоих торцов силой F.

Диаграмма сжатия стержня имеет вид (рис. 10, а)

где Δl = l — l0 абсолютное удлинение стержня; ε = Δl / l0 — относительное продольное удлинение стержня; σ = F / A0 — нормальное напряжение; E — модуль Юнга; σп — предел пропорциональности; σуп — предел упругости; σт — предел текучести; σв — предел прочности (временное сопротивление); εост — остаточная деформация после снятия внешних нагрузок. Для материалов, не имеющих ярко выраженную площадку текучести, вводят условный предел текучести σ0,2 — напряжение, при котором достигается 0,2% остаточной деформации. При достижении предела прочности в центре стержня возникает локальное утончение его диаметра («шейка»). Дальнейшее абсолютное удлинение стержня идет в зоне шейки ( зона местной текучести). При достижении напряжением предела текучести σт глянцевая поверхность стержня становится немного матовой – на его поверхности появляются микротрещины (линии Людерса-Чернова), направленные под углом 45° к оси стержня.

Расчеты на прочность и жесткость при растяжении и сжатии.
Опасным сечением при растяжении и сжатии называется поперечное сечение бруса, в котором возникает максимальное нормальное напряжение. Допускаемые напряжения вычисляются по формуле:
где σпред — предельное напряжение (σпред = σт — для пластических материалов и σпред = σв — для хрупких материалов); [n] — коэффициент запаса прочности. Для пластических материалов [n] = [nт] = 1,2 … 2,5; для хрупких материалов [n] = [nв] = 2 … 5, а для древесины [n] = 8 ÷ 12.
Расчеты на прочность при растяжении и сжатии.
Целью расчета любой конструкции является использование полученных результатов для оценки пригодности этой конструкции к эксплуатации при минимальном расходе материала, что находит отражение в методах расчета на прочность и жесткость.
Условие прочности стержня при его растяжении (сжатии):
При проектном расчете определяется площадь опасного сечения стержня:
При определении допускаемой нагрузки рассчитывается допускаемая нормальная сила:
Расчет на жесткость при растяжении и сжатии.
Работоспособность стержня определяется его предельной деформацией [ l ]. Абсолютное удлинение стержня должно удовлетворять условию:
Часто дополнительно делают расчет на жесткость отдельных участков стержня.
Следующая важная статья теории:
Изгиб балки
Источник
