Расчет подкоса на растяжение
Главная
Расчеты на растяжение и сжатие
статически определимых стержневых систем
Пример 1.
Абсолютно
жесткий брус ВС (ЕВС = ) прикреплен в точке С к неподвижному шарниру (см.
рис.), а в точке В поддерживается
стальной тягой АВ. В точке В приложена вертикальная сила F = 20 кН.
Подобрать
сечение тяги АВ и показать перемещение
точки В. Расчетное сопротивление
стали растяжению коэффициент условий работы а модуль упругости
стали тяги АВ –
Решение.
Вырежем
мысленно узел В (рис. б) и составим для него уравнения
равновесия:
откуда находим
откуда
Окончательно
имеем
Следовательно,
брус ВС сжат силой N2, а элемент АВ растянут силой N1.
Подбор сечения
тяги АВ проводим по формуле откуда определяем
Предположим,
что тяга АВ имеет круглое поперечное
сечение, тогда An =
1,44 см2 = , откуда находим r =
0,677 смиd = 1,35 см.
Определим
удлинения стержней АВ и СВ:
Таким образом, точка В переместится в точку В/
по дуге окружности радиусом , причем расстояние между точками А и В/будет равно
Пример 2.
Определить из расчетов на прочность и жесткость
допускаемую силу F, если [] = 120 МПа, [] = 1,7 мм, А1 = 2А, А2 = А = 5 см2, l1 = l2 = l = 1 м, Е = 200 ГПа.
Р е ш е н и е.
1. Определение усилий в стержнях.
Из условия равновесия бруса АС имеем
, , ;
, , .
2. Расчет на прочность.
Находим напряжения в
стержнях
,
.
Как видим, наиболее
нагруженным является 2-й стержень, прочность которого предопределяет прочность
всей конструкции в целом. Из условия прочности находим = 30 кН.
3. Расчет на жесткость.
Вычисляем деформации
стержней
,
,
а по ним перемещение точки С. Из подобия треугольников В1А1В2 и С1А1С2 имеем:
В1В2/А1В2 = С1С2/А1С2 или ,
откуда .
Записываем условие жесткости ,
откуда = 200×109×5×10-4×1,7×10-3/(8,5×1)= 20 кН.
Допускаемая нагрузка из расчета на жесткость
получилась меньше, чем из расчета на прочность, поэтому ее и принимаем в качестве окончательной, т.е.
кН.
Пример 3.
К двум
одинаковым стержням приложена сила F.
Установить, при каком угле конструкция будет
иметь наименьший вес?
Р е ш е н и е.
Вес
конструкции является функцией угла , т.е. .
Нам необходимо установить такой угол, при котором
функция принимает минимальное значение. В теории оптимального
проектирования она называется целевой функцией.
Для
определения веса стержневой системы нужно знать площади сечений стержней. Из
условия равновесия узла С находим
усилия в стержнях:
, , ,
а из условия
прочности – площади их поперечных сечений:
, откуда .
Учитывая, что
длины стержней , находим вес конструкции (целевую функцию):
.
Функция принимает минимальное
значение, когда
, откуда и .
Определение грузоподъемности
статически определимой конструкции, работающей на растяжение-сжатие. Расчет по
допускаемым напряжениям
При таком
подходе несущая способность конструкции отождествляется с несущей способностью
наиболее нагруженного элемента. Последовательность расчета при этом выглядит
следующим образом.
Составляются уравнения статики и по числу лишних неизвестных –
дополнительные уравнения совместности деформаций. Решая полученную систему,
определяют усилия в стержнях и связанные с ними напряжения. Из сопоставления
напряжений в наиболее нагруженном элементе с допустимой величиной делается
заключение о надежности конструкции либо определяются искомые величины (размеры
сечения стержней, допускаемая нагрузка).
Пример 4.
Конструкция,
состоящая из стержней, соединенных шарнирами, загружена силой F (см. рис. 1). Сечения стержней – из
прокатной стали и площади сечений можно найти по таблицам сортамента прокатной
стали. Цель расчета:
1. определить
значение допускаемой нагрузки;
2. найти
перемещение узла С.
Рис.1
Решение.
Для
определения усилий используем метод сечений. Для этого нарисуем план сил
(рис.2): рассечем деформируемые стержни конструкции и отброшенные части
стержней заменим продольными силами N1 и N2 .
Рис.2
Из уравнений
равновесия отсеченной части конструкции найдем продольные силы в стержнях:
и .
Знак минус показывает,
что направление усилия в стержне 2 противоположно показанному на плане сил,
т.е. стержень 2 сжат.
Определим
напряжения по и выберем наиболее напряженный стержень (допустим, что в рассматриваемой задаче
это будет стержень 1).
Из условия прочности этого стержня получим значение
допускаемой нагрузки:
, .
Найдем
перемещение узла С,
построив план перемещений (рис.3).
Рис.3
Предварительно
найдем абсолютные деформации стержней и по формуле . В
рассматриваемой задаче растянутый стержень 1 будет удлиняться, а сжатый
стержень 2 – укорачиваться. Для построения плана перемещений нарисуем схему
конструкции в масштабе и отложим отрезки и вдоль оси каждого
стержня, выбрав масштаб для деформаций так, чтобы картинка плана перемещений
была наглядной. В процессе деформации стержни поворачиваются относительно точек
А и В по дугам. Из-за малости деформаций эти дуги заменяем
касательными, т. е. перпендикулярами к направлениям стержней (отрезки и на плане перемещений).
На пересечении дуг (перпендикуляров к направлениям стержней) находится новое
положение узла C после деформации –
точка на плане перемещений.
Вертикальное и горизонтальное перемещение узла C допускается определять по масштабу, не делая сложных
геометрических выкладок.
Примечание. Если конструкция имеет
абсолютно жесткий стержень, то принцип
построения плана перемещений тот же. Все точки абсолютно жесткого стержня могут
перемещаться только по дугам (перпендикулярам к направлению стержня), поворачиваясь
вокруг неподвижного шарнира. Например, если стержень АС на плане перемещений считать абсолютно жестким, то точка Спереместится в положение и горизонтальное
перемещение узла С будет равно нулю.
Пример 5.
Для схемы, изображенной на рис.1 необходимо:
Рис.1
1) Определить площадь поперечного сечения стержней при действии силы F и подобрать угловую равнополочную
или неравнополочную сталь, при условии, что поперечное
сечение одного из стержней в два раза больше, чем другого.
2) Определить напряжения в стержнях:
— от действия силы F;
— от неточности монтажа, если считать, что один из стержней выполнен
короче на величину ;
— от изменения температуры.
3) Определить суммарные напряжения от действия внешних сил, от неточности
монтажа и от изменения температуры.
4) Подсчитать недонапряжения или перенапряжения
в стержнях.
Дано: F=100 кН, а =
1,2м, b = 0,8м, = 0,2мм, = 20°С, Е = 2×105МПа,
= 125×10-71/гр, [] = 100 МПа.
Решение.
Определим необходимую по условию прочности площадь поперечного сечения
стержней.
1) Находим степень статической неопределимости.
2.1) Статическая сторона задачи
; ;
; ;
; .
2.2) Геометрическая сторона задачи (рис.2)
~Þ
; ; ;
2.3) Физическая сторона задачи
;
Рис.2
2.4) Синтез
Подставим выражения, полученные в физической стороне задачи, в выражения
из геометрической стороны задачи и приведем подобные.
Решим совместно систему уравнений, составленную из полученного выражения
для N1 и уравнения моментов из статической стороны
задачи.
2.5) Определяем площадь поперечного сечения стержней
Определим, какой из стержней нагружен сильнее.
;
Второй стержень является более нагруженным, так как , поэтому запишем для него условие прочности и
определим площадь поперечного сечения.
Подбираем по справочнику угловую равнополочную сталь № 70´5
ГОСТ8509-86 (SТ= 6,86 см2).
2.6) Определяем напряжения в стержнях от внешних сил
Первый стержень работает на сжатие, а второй – на растяжение.
3) Определим напряжения в стержнях от неточности монтажа
Будем считать, что короткий стержень выполнен короче на величину (см.рис.3).
Рис.3
3.1) Статическая сторона задачи
; ;
; ;
; .
3.2) Геометрическая сторона задачи
~Þ
; ; ;
3.3) Физическая сторона задачи
;
3.4) Синтез
Подставим в полученное выражение данные из условия задачи и получим:
3.5) Определим напряжения в стержнях
Оба стержня работают на растяжение.
4) Определим напряжения в стержнях от изменения температуры (см. рис. 4).
Рис.4
Будем считать, что температура системы повышается. Тогда оба стержня будут
удлиняться от повышения температуры. При удлинении стержней, они будут
воздействовать друг на друга через недеформируемый стержень АС. Вследствие этого, в обоих стержнях
будут возникать дополнительные силы сжатия.
4.1) Статическая сторона задачи
; ;
; ;
; .
4.2) Геометрическая сторона задачи
~Þ
; ; ;
4.3) Физическая сторона задачи
;
.
4.4) Синтез
Решив уравнение, получим .
4.5) Определим напряжения в стержнях
Оба стержня работают на сжатие.
5) Определим суммарные напряжения в стержнях
6) Найдем недонапряжения или перенапряжения в
стержнях
— недонапряжение
— недонапряжение.
Пример 6.
Дано: Сила F= 100 кН;
расчетное сопротивление стали R =160 МПа; модуль упругости E=2∙105
МПа(рис. а)
Требуется:
1. Определить
усилия в стержнях.
2. Подобрать
размеры поперечных сечений стержней. Стержень 1 стальной, круглого поперечного
сечения, стержень 2 стальной квадратного сечения.
3. Вычислить
удлинения (укорочения) стержней и построить план перемещений.
4. Определить
перемещение узла.
а)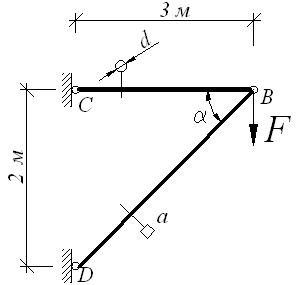 б)
б)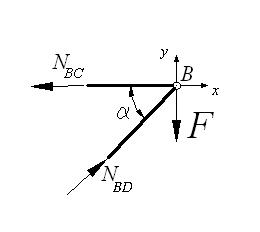
в)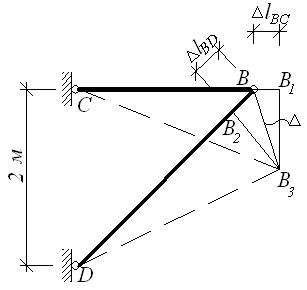 г)
г)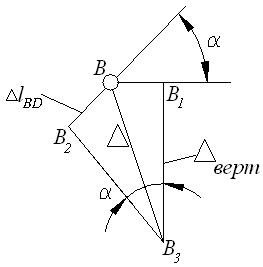
Решение.
Мысленно
вырезаем узел В,
действие отброшенной части кронштейна заменяем искомыми внутренними усилиями.
Для полученной плоской системы сходящихся сил составим уравнения равновесия
(рис. б)
Решив
уравнения, найдем внутренние усилия NBD и NBC
Полученные
положительные значения внутренних усилий показывают, что предварительно
выбранные направления усилий оказались верными, стержень BC
растягивается, а стержень BD сжимается.
Диаметр
стержня BC находим из условия прочности:
где,
откуда .
Размеры поперечного сечения стержня BD определим на условия
прочности:
где ABD = a2,
откуда .
Перемещение
узла В
найдем с помощью графоаналитического метода, для чего вычислим, используя закон
Гука, абсолютные деформации стержней ВС
и BD, предполагая их свободными в точке В:
где
Положение узла В после деформации стержней
определится в результате построения
деформационного треугольника по сторонам и .
Стержень ВС удлинился на величину , концевое сечение
переместилось в точку В1. Радиусом, равным СВ1проведем из точки С
дугу окружности. Так как перемещения малы, то дугу можно заменить касательной,
проведенной через В1
перпендикулярно оси стерня ВС
(рисунок 1, в).
Стержень BD укоротился на , и концевое сечение переместилось в точку В2.
Заменяя дугу, описанную из точки D радиусом DB2касательной,
проведенной через В2перпендикулярно оси стержня BD, получим на
пересечении перпендикуляров точку В3
— новое положение узла В. Соединив
точку В с В3 найдем перемещение узла В. На рисунке 1, в план перемещений изображен в увеличенном масштабе. План
перемещений рекомендуется строить отдельно, как показано на рисунке 1, г. Из него следует, что горизонтальная
составляющая перемещения узла
В равна:
см.
Вертикальную
составляющую перемещения узла
В легко найти,
воспользовавшись теоремой аналитической геометрии – проекция замыкающей на
любую ось равна алгебраической сумме проекций составляющих на ту же ось. Принимая за ось проекций направление получим:
;
откуда .
Знак учтен при построении
плана перемещений. Полное перемещение узла Вбудет равно:
.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин
Теория машин и механизмов
Источник

Рисунок 251.1. Данные для определения высоты опорной стойки и подкосов.
При такой стропильной схеме высота стойки составляет приблизительно h = 1.75 м (определяется через тангенс угла α, h = b1tgα — 0.05 м, где 0.05 м — приблизительная высота коньковой балки с учетом врубки). Длина подкоса приблизительно lп = 1.7 м (определяется по теореме косинусов для треугольника, так как по принципу подобия треугольников найдена одна сторона треугольника l2 = 1.4 м, то lп2 = h2 + l22 — 2hl2cosγ). Сечения стропил и обрешетки уже определены. В статье: «Двухпролетные балки» показано, как можно определить опорные реакции для стропильной ноги в данном случае являющейся двухпролетной балкой. При указанных пролетах А =1. 0556q B = 2.6978q C = 0.2464q. Для подкосов расчетной нагрузкой будет опорная реакция В, умноженная на синус угла, образованного стропилом и подкосом. Как следует из рисунка 251.1 этот угол составляет 180 — 45 — 63 = 72о, соответственно синус этого угла составит 0.951. Тогда:
Nподкосов = 2.6978·326.1·0.951 = 836.7 кг.
Для стойки расчетной нагрузкой будет сумма опорных реакций от левой и правой стропильных ног. При определении сечения стропил мы использовали максимальное значение снеговой нагрузки:
qsлев = 180х1.25х1.2 = 270 кг/м.
Однако по принятой расчетной схеме снеговая нагрузка для противоположной стропильной ноги будет меньше:
qsправ = 180х0.75х1.2 = 162 кг/м.
тогда:
qправ = qcт + qo + qш +qsправ = 3.75 + (6.25 + 16.77 +162)1.1 = 207.27 кг/м
Таким образом суммарная нагрузка на опорную стойку составит:
Nстойки = 0.2464(326.1 + 207.27) = 131.42 кг
Требуется:
Подобрать сечение опорной стойки (показана ни рисунке 251.1 оранжевым цветом) и подкосов (показаны на рисунке 251.1 фиолетовым цветом). Основные принципы расчета сжимаемых элементов изложены отдельно.
Решение:
Даже у такой, казалось бы простой задачи есть два варианта решения.
1 Вариант
Можно подобрать сечение элементов по расчетной нагрузке, однако для этого нужно знать радиус инерции сечения. Понимаю, что многие люди даже приблизительно не знают, что такое радиус инерции, ну а те кто знают, скажут, что для определения радиуса инерции нужно знать высоту и ширину сечения, а ведь именно это нам и нужно определить. Это действительно так, а еще после того, как радиус инерции известен, нужно сначала определить гибкость элемента, после этого коэффициент продольного изгиба и только потом можно определить требуемое сечение. Окончательная формула для проверки сжимаемого элемента на устойчивость достаточно проста:
σ = N/φF ≤ Rc (250.1.2)
Конечно математический аппарат позволяет решать такие задачи, однако намного проще выполнить расчет по второму варианту.
2 Вариант
Из конструктивных и технологических соображений или просто интуитивно можно сначала принять предварительно сечение элементов, а затем проверить их на устойчивость. Все равно выбор пиломатериалов по сечению сильно ограничен по сравнению с металлопрокатом и подобрать сечение так, чтобы элементы были загружены на 95-100% вряд ли получится. В данном случае, так как стропила имеют сечение 5х15 см, то сечения опорной стойки 5х5 см (если верить моей интуиции) будет вполне достаточно, а для подкосов хватит сечения 5х10 см (опять же интуиция подсказывает, но и из конструктивных соображений — для надежного соединения стропильной ноги и подкоса). Из конструктивных соображений (чтобы уменьшить количество типоразмеров при закупке делового леса) примем предварительно сечения и опорной стойки и подкосов 5х10 см.
Примечание: В принципе при столь небольших нагрузках на опорные стойки можно вообще обойтись без коньковой балки, опорная стойка может сразу подпирать стропила, но это уже вопрос удобства выполнения крыши (ведь возможно потребуется обеспечить геометрическую неизменяемость стропильной системы в плоскости, перпендикулярной показанной на рисунке 251.1, проще говоря вдоль дома), поэтому в расчетных схемах ничего менять не будем, к тому же возможные варианты стропильных систем здесь не обсуждаются.
Так как нагрузка на подкосы почти в 7 раз больше, чем нагрузка на стойки, то при принятых одинаковых сечениях стоек и подкосов и при приблизительно одинаковой расчетной длине достаточно проверить на устойчивость только подкосы.
Расчетная длина подкосов равна реальной длине lп = lo = 170 см. При ширине подкоса 5 см радиус инерции составит:
iy = (Iy/F)1/2 = (b2/12)1/2 = (52/12)1/2 = 1.44 см
теперь можно определить гибкость стропильной ноги относительно оси z:
λ = lo/iy = 170/ 1.44 = 117.78 (250.1.5)
Проверим допустимость такого значения гибкости. СНиП II-25-80 (1988) рекомендует принимать для рассчитываемых деревянных элементов такие значения гибкости, которые не превышают значения, приведенные в таблице
Таблица 1. Предельные значения гибкости (согласно СНиП II-25-80 (1988))

В нашем случае конструкцию сложно назвать фермой, согласно таблицы 1 это скорее другая сквозная конструкция и тогда предельно допустимая гибкость для нашей стойки λ = 150. Тем не менее при выполнении непрофессиональных расчетов я все-таки рекомендую использовать более строгие ограничения и принимать предельно допустимую гибкость для деревянных стоек и подкосов конструкций кровли λ ≤ 120. Полученное нами значение меньше предельно допустимого (117.78 < 120), а потому можно продолжать расчет.
так как λ > 70, то φ = А/λ2
где А = 3000 для древесины (А = 2500 для фанеры), то
φ = 3000/117.782 = 0.2163
Расчетное сопротивление древесины (2 сорт) сжатию вдоль волокон — Rс = 130 кгс/см2(согласно СНиП II-25-80 (1988)). Площадь выбранного нами сечения F = 5х10 = 50 см2.
Теперь по формуле (250.1.2) мы можем определить достаточно ли выбранного нами сечения:
836.7/(0.2163·50) = 77.36 < 130 кг/см2.
Как видим, такого сечения подкосов вполне достаточно и даже с запасом на возможные случайные эксцентриситеты приложения нагрузки. Можно даже использовать брус сечением 5х7 см для подкосов (но в этом случае расчет желательно выполнить с учетом случайного эксцентриситета), а уж для опорных стоек так тем более. Но из соображений удобства монтажа лучше оставить выбранное сечение.
Примечание: при значении гибкости λ < 70 коэффициент изгиба определяется по формуле:
φ = 1 — а(λ/100)2
где а = 0.8 — для древесины, а = 1 — для фанеры
Все необходимые формальности нами соблюдены, но желательно также проверить стропильную ногу на смятие в месте контакта с подкосом.
Расчетное сопротивление древесины смятию в опорных частях конструкций, лобовых врубках и узловых примыканиях элементов (смятие поперек волокон) — Rсм90 = 30 кгс/см2 (согласно СНиП II-25-80 (1988)).
σ = N/F ≤ Rcм90 = 836.7/50 = 16.7 < 30 кгс/см2 (1.1)
Вот, в общем-то и весь расчет.
02-05-2013: Николай
Спасибо — добрался и сюда.
Посмотрев на приведенное описание я вижу, что на вертикально стоящую балку 10*5 см можно спокойно сверху 880кг и при этом останется запас прочности в 40% (81.34/130) — я правильно понял логику?
03-05-2013: Доктор Лом
Не совсем. В вашем случае расчетная длина будет не 170 см, а 280 см, поэтому и нагрузка, которую выдержит стойка, будет меньше. Но если вы свяжете стойки дополнительно посредине, то уменьшите расчетную длину стоек и тогда стойки выдержат еще большую нагрузку
06-01-2014: Сергей
Поясните, пожалуйста,почему при расчете на смятие вы использовали значение расчетной нагрузки для подкосов N=879,75, тогда как выше она была расчитана как N=836,7 кг.?
06-01-2014: Доктор Лом
Результат небрежного форматирования. Исправил.
11-09-2014: Николай
Здравствуйте, Доктор Лом.
Если я не ошибаюсь, то у Вас опечатка в формуле
lп = h^2 + l2^2 — 2*h*l2*cos?, — lп здесь должно быть в квадрате (теорема косинусов).
11-09-2014: Доктор Лом
Да, действительно, опечатка. Спасибо за внимательность, исправил.
12-09-2014: Николай
Доброго времени суток, Док.
Кажется, нашёл ещё опечатку в предложении «При указанных пролетах А = 0.556q B = 2.6978q C = 0.2464q.». На самом деле A = 1.0558.
13-09-2014: Доктор Лом
Ай молодец. Все верно, исправил.
09-03-2015: Михаил
Спасибо за наглядное объяснение! подскажите, почему не умножили расчетное сопротивление на коэф-т Мб=0.8 (высота сечения более 120см) по пункту 5.2д и табличке 9 согласно СНиП II-25-80? на результат то не особ повлияет, но все ж..
09-03-2015: Доктор Лом
Указанный вами коэффициент Мб используется при расчете изгибаемых, внецентренно-сжатых, сжато-изгибаемых и сжатых клееных элементов прямоугольного сечения, а коэффициент Мгн — для гнутых элементов. В статье рассматривается расчет центрально сжатого прямолинейного элемента.
Тем не менее любой запас прочности, который происходит при использовании понижающего коэффициента, я приветствую.
27-11-2018: Евгений
Привет!
Скажите, для детской кровати типа чердак h 2000 -2200 мм, размер спального места 900 х 2000 мм, (ребёнок 20 -40 кг) стойки (по углам) сечением 50 х 50 мм достаточно?
28-11-2018: Доктор Лом
Тут все не так просто. Формально такого сечения при строго вертикальной нагрузке хватит с избытком. Однако возможны технологические ослабления сечения (к стойкам нужно как-то крепить спальное место). А кроме того, в бытовых условиях нагрузки могут быть далеко не всегда вертикальными, но еще и горизонтальными. Это также нужно учитывать.
Источник
