Расчет по предельному равновесию при растяжении
Сопротивление материалов
Решение задач на растяжение и сжатие
Расчеты на прочность при растяжении и сжатии
В результате проведения механических испытаний устанавливают предельные напряжения, при которых происходит нарушение работы или разрушение деталей конструкции.
Предельным напряжением при статической нагрузке для пластичных материалов является предел текучести, для хрупких — предел прочности.
Для обеспечения прочности деталей необходимо, чтобы возникающие в них в процессе эксплуатации наибольшие напряжения были меньше предельных.
Отношение предельного напряжения к напряжению, возникающему в процессе работы детали, называют коэффициентом запаса прочности и обозначают буквой s:
s = σпред / σ,
где σ = N / А – реальное напряжение, возникающее в элементе конструкции.
Недостаточный коэффициент запаса прочности может привести к потере работоспособности конструкции, а избыточный (слишком высокий) — к перерасходу материала и утяжелению конструкции. Минимально необходимый коэффициент запаса прочности называют допускаемым, и обозначают [s].
Отношение предельного напряжения к допускаемому запасу прочности называют допускаемым напряжением, и обозначают [σ]:
[σ] = σпред / [s].
Условие прочности в деталях и конструкциях заключается в том, что наибольшее возникающее в ней напряжение (рабочее напряжение) не должно превышать допускаемого:
σmax≤ [σ], или в другом виде: s ≥ [s].
Если допускаемые напряжения при растяжении и сжатии различны, их обозначают [σр] и [σс].
Расчетная формула при растяжении и сжатии имеет вид:
σ = N / А ≤ [σ]
и читается следующим образом: нормальное напряжение в опасном сечении, вычисленное по формуле σ = N /А, не должно превышать допустимое.
На практике расчеты на прочность проводят для решения задач:
— проектный расчет, при котором определяются минимальные размеры опасного сечения;
— проверочный расчет, при котором определяется рабочее напряжение и сравнивается с предельно допустимым;
-определение допускаемой нагрузки при заданных размерах опасного сечения.
***
Растяжение под действием собственного веса
Если ось бруса вертикальна, то его собственный вес вызывает деформацию растяжения или сжатия. 
Рассмотрим брус постоянного сечения весом G, длиной l, закрепленный верхним концом и нагруженный только собственным весом G (рис.1).
Для определения напряжений в поперечном сечении на переменном расстоянии z от нижнего конца применим метод сечений.
Рассмотрим равновесие нижней части бруса и составим уравнение равновесия:
Σ Z = 0; Nz — Gz = 0, откуда:
Nz = Gz = γ А z,
где γ — удельный вес материала бруса, А – площадь его поперечного сечения, z — длина части бруса от свободного конца до рассматриваемого сечения.
Напряжения, возникающие в сечениях бруса, нагруженного собственным весом, определяются по формуле:
σz = Nz / А = γ А z / А = γ z,
т. е. для нагруженного собственным весом бруса нормальное напряжение не зависит от площади поперечного сечения. Очевидно, что опасное сечение будет находиться в заделке:
σmax = γ l.
Эпюра распределения напряжений вдоль оси бруса представляет собой треугольник.
Если требуется определить максимальную длину бруса, нагруженного собственным весом, используют расчет по предельному допустимому напряжению в сечении:
lпр = [σ] / γ.
***
Статически неопределимые задачи
Иногда в практике расчета конструкций требуется определить неизвестные силовые факторы (например, реакции связей или внутренние силы), при этом количество неизвестных силовых факторов превышает количество возможных уравнений равновесия для данной конструкции, и расчет произвести рассмотренными ранее способами не представляется возможным.
Задачи на расчет конструкций, в которых внутренние силовые факторы не могут быть определены с помощью одних лишь уравнений равновесия статики, называют статически неопределимыми. Подобные задачи нередко встречаются при расчете конструкций, подверженных температурным деформациям.
Для решения таких задач помимо уравнений равновесия составляют уравнение перемещений или деформаций.
Рассмотрим невесомый стержень постоянного сечения площадью А, длиной l, жестко защемленный по концам (см. рис. 2). 
При нагревании в стержне возникают температурные напряжения сжатия.
Попробуем определить эти напряжения.
Составим для стержня уравнение равновесия:
Σ Z = 0; RС — RВ = 0,
откуда следует, что реакции RС и RВ равны между собой, а применив метод сечений установим, что продольная сила N в сечениях стержня равна неизвестным реакциям:
N = RС = RВ.
Составим дополнительное уравнение, для чего мысленно отбросим правую заделку и заменим ее реакцией RВ, тогда дополнительное уравнение деформации будет иметь вид:
Δlt = ΔlСВ
т. е. температурное удлинение стержня равно его укорочению под действием реакции RB, так как связи предполагаются абсолютно жесткими.
Температурное удлинение стержня определяется по формуле: Δlt = αtl, где α — коэффициент линейного расширения стержня.
Укорочение стержня под действием реакции: ΔlСВ = RB l / (EА).
Приравняв правые части равенств, получим:
αtl = RB l / (EА), откуда RB = αtEА.
Температурные напряжения в реальных конструкциях могут достигать значительных величин. Чтобы исключить их отрицательное влияние на прочность конструкций, прибегают к различным методам. Мосты, например, закрепляют лишь на одном конце (на одном берегу), а второй конец оставляют подвижным.
В длинных трубопроводах, подверженных температурным напряжениям, делают компенсирующие карманы, петли и т. д.
***
Материалы раздела «Растяжение и сжатие»:
- Примеры решения задач по сопромату.
- Основные понятия о деформации растяжения и сжатия.
- Деформации при растяжении и сжатии. Потенциальная энергия деформации растяжения.
Срез
Правильные ответы на вопросы Теста № 6
№ вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Правильный вариант ответа | 2 | 1 | 1 | 3 | 3 | 2 | 1 | 3 | 2 | 1 |
Источник
Для статически
определимой системы, в элементах которой
возникают лишь продольные усилия,
расчеты на прочность по допускаемым
напряжениям и по предельным нагрузкам
дают один и тот же результат. Результаты
аналогичных расчетов статически
неопределимой системы различны.
В качестве примера
рассмотрим систему, представляющую
собой абсолютно жесткую балку, с одним
концом шарнирно опертую, и подвешенную
на трех одинаковых идеально
упруго-пластических
подвесках, длиной l,
площадью поперечного сечения F,
модулем упругости материала Е,
при заданной схеме нагружения силой Р
(рис.23.1, а).
Заданная система дважды статически
неопределима.
По мере роста силы
P,
подвески 1, 2, 3 поэтапно будут переходить
в пластическое состояние, причем
напряжения в каждой подвеске не могут
превышать
![]() .
.
Выделим следующие
стадии деформирования заданной системы.
Первая стадия:
все подвески работают упруго. Для
определения реакций в подвесках
составляем уравнения равновесия:
.
(23.1)
Для определения
величин усилий в подвесках N1,
N2
и N3
необходимо составить еще два уравнения
совместности. Учитывая, что балка
абсолютно жесткая и деформации в
подвесках пропорциональны возникающим
в них усилиям, то из условия подобия
треугольников ADD’,
ACC’
и ABB’
(рис.23.1), имеем:
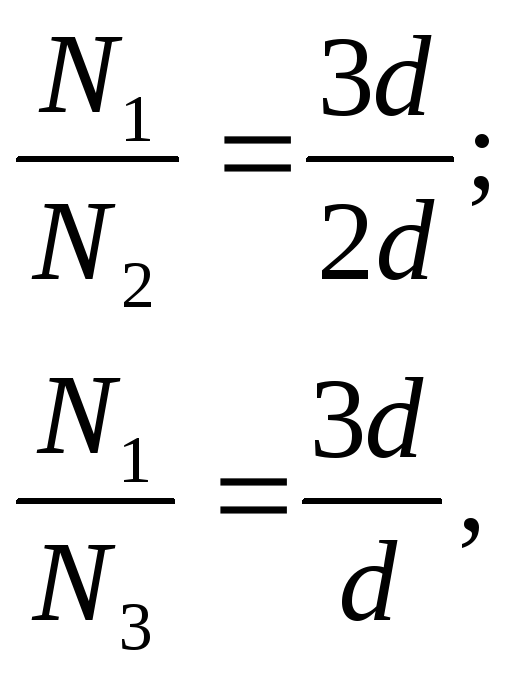
откуда
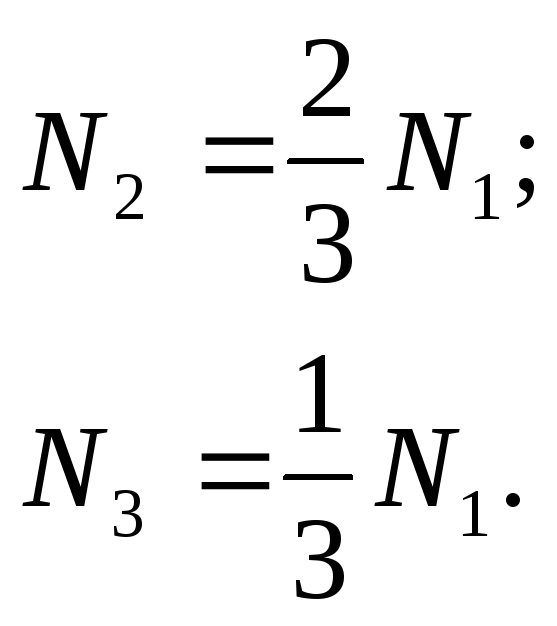
(23.2)
Тогда из (23.1) с
учетом (23.2) определяются реакции во всех
подвесках:
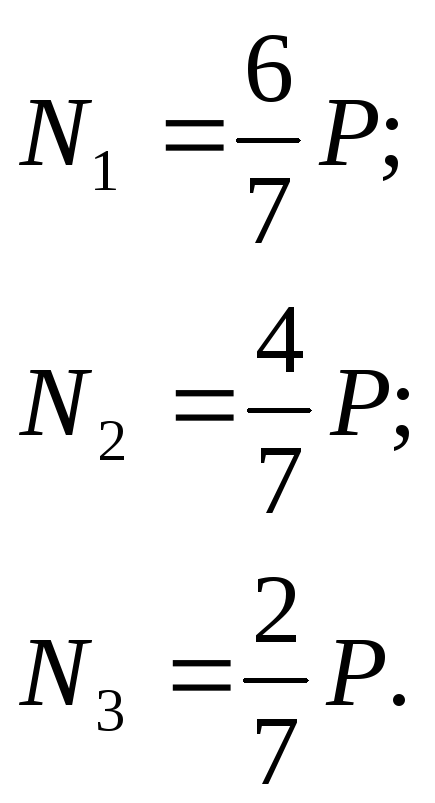
(23.3)
Вторая стадия: при
некотором значении P,
как это следует из (23.3), сначала наиболее
нагруженная первая подвеска, переходит
в пластическое состояние, то есть
![]() (рис.23.1,б).
(рис.23.1,б).
При этом из (23.2) можно установить, что в
остальных подвесках усилия будут равны:
![]() ;
;
![]() .
.
(23.4)
Подставляя значения
усилий в уравнение равновесия (23.1),
получим:
![]() ,
,
откуда и определим
величину внешней силы Р,
при котором система переходит во второе
состояние:
![]() .
.
(23.5)
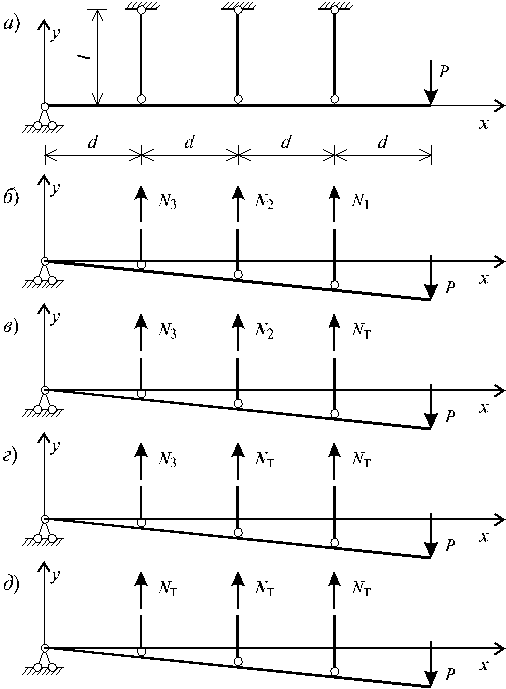
Рис.23.1
Третья стадия:
при дальнейшем росте значения силы P,
как это следует из (23.3), и вторая подвеска
переходит в пластическое состояние, то
есть N1 = N2 = ![]() (рис.23.1,в).
(рис.23.1,в).
При этом, из третьего соотношения (23.3),
значение усилия в третьей подвеске
будет равно:
![]() .
.
(23.6)
Из уравнения
равновесия (23.1), с учетом значения усилий
в подвесках в третьем состоянии, получим:
![]() .
.
(23.7)
Четвертая
стадия — предельное
состояние:
в этом состоянии усилия во всех трех
подвесках равны своему предельному
значению, т.е.
![]() (рис.23.1,г).
(рис.23.1,г).
Уравнение равновесия (23.1), при этом
принимает вид:
![]() ,
,
(23.8)
откуда и определяется
предельная величина внешней силы:
![]() .
.
(23.9)
Далее определим
перемещение fiбалки в точке
приложения внешней силы P
в различных стадиях работы заданной
системы.
При переходе
заданной системы от первого стадии
деформирования ко второму, имеем:
![]() ;
;
![]() .
.
При переходе
заданной системы от второй стадии к
третьей, имеем:
![]() ;
;
![]() .
.
И наконец, при
переходе системы от третьей стадии к
предельному состоянию, получим:
![]() .
.
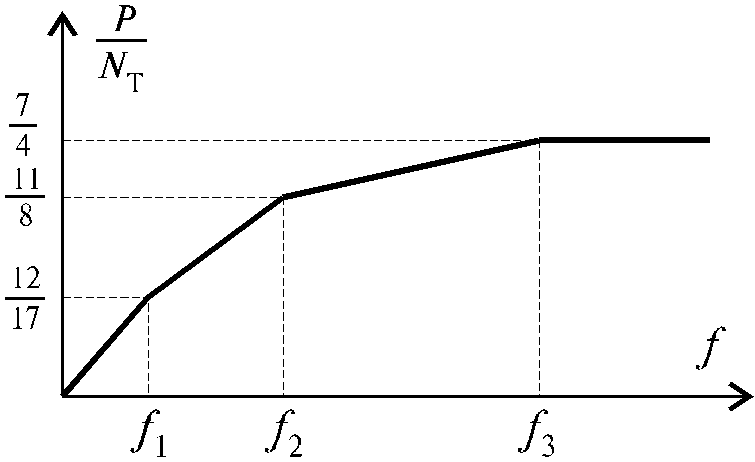
Рис.23.2
Зависимость f от
P показана на рис.23.2. Она изображается
ломаной линией, которая после предельного
равновесного состояния становится
горизонтальной, то есть после того, как
напряжения достигнут предела текучести
во всех трех подвесках. Откуда следует,
что при постоянной
![]() ,
,
перемещение f беспредельно возрастает,
т.е. происходит разрушение системы.
Как видно из
приведенного примера, расчет даже для
такой простой системы оказывается
довольно громоздким, хотя он дает
возможность находить не только предельную
силу, но и описать поведение конструкции
в процессе ее нагружения. На практике,
при расчете систем с учетом пластических
деформаций рассматривают только
предельное состояние.
Соседние файлы в папке Лекции
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник



2.4. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ РАСТЯЖЕНИИ Основной задачей расчета конструкции на растяжение является обеспечение ее прочности в условиях эксплуатации. Условие прочности – оценка прочности элемента конструкции, сводящаяся к сравнению расчетных напряжений с допускаемыми: σ≤рσ[р ]; σ с ≤[ с],σ (2.9) где σр и σс – наибольшие расчетные растягивающие и сжимающие напряжения; [σр] и [σс] – допускаемые напряжения при растяжении и сжатии. Допускаемое напряжение – наибольшее напряжение, которое можно допустить в элементе конструкции при условии его безопасной, долговечной и надежной работы: Здесь σпред – предельное напряжение (состояние), при котором конструкция перестает удовлетворять эксплуатационным требованиям; им мо- гут быть предел текучести, предел прочности, предел выносливости, пре- дел ползучести и др. Для конструкций из пластичных материалов при определении допускаемых напряжений используют предел текучести σт (рис. 2.4, а). Это связано с тем, что в случае его превышения деформации резко возрастают при незначительном увеличении нагрузки и конструкция перестает удовлетворять условиям эксплуатации. Допускаемое напряжение в этом случае определяют как Для хрупких материалов (чугун, бетон, керамика) где σвр и σвс – пределы прочности при растяжении и сжатии (рис. 2.4, б). Здесь [n] – нормативный коэффициент запаса прочности. В зависимости от той предельной характеристики, с которой сравнивают расчетное напряжение σ, различают [nт] – нормативный коэффициент запаса прочности по отношению к пределу текучести σт и [nв] – нормативный коэффициент запаса прочности по отношению к пределу прочности σв. Запас прочности – отношение предельно допустимой теоретической нагрузки к той нагрузке, при которой возможна безопасная работа конструкции с учетом случайных перегрузок, непредвиденных дефектов и недостоверности исходных данных для теоретических расчетов. Нормативные коэффициенты запаса прочности зависят: − от класса конструкции (капитальная, временная), − намечаемого срока эксплуатации, − условий эксплуатации (радиация, коррозия, загнивание), − вида нагружения (статическое, циклическое, ударные нагрузки) − неточности задания величины внешних нагрузок, − неточности расчетных схем и приближенности методов расчета − и других факторов. Нормативный коэффициент запаса прочности не может быть единым на все случаи жизни. В каждой отрасли машиностроения сложились свои подходы, методы проектирования и приемы технологии. В изделиях общего машиностроения принимают [nт] = 1,3 – 2,2; [nв] = 3 – 5. Вероятность выхода из строя приближенно можно оценить с помощью коэффициента запаса в условии прочности: n = 1 соответствует вероятности невыхода из строя 50 %; n = 1,2 соответствует вероятности невыхода из строя 90 %; n = 1,5 соответствует вероятности невыхода из строя 99 %; n = 2 соответствует вероятности невыхода из строя 99,9 %. Для неответственных деталей n = 2 много. Для ответственных – мало. Так для каната подъемного лифта это означает на 1000 подъемов одно падение. При расчете конструкций на прочность встречаются три вида задач, которые вытекают из условия прочности а) поверочный расчет (проверка прочности). Известны усилие N и площадь A. Вычисляют σ = N/A и, сравнивая его с предельным σт или σв (для пластичного и хрупкого материалов соответственно), находят фактический коэффициент запаса прочности который затем сопоставляют с нормативным [n]; б) проектный расчет (подбор сечения). Известны внутреннее усилие N и допускаемое напряжение [σ]. Определяют требуемую площадь поперечного сечения стержня в) определение грузоподъемности (несущей способности). Известны площадь А и допускаемое напряжение [σ]. Вычисляют внутреннее усилие N≤N[ ] = ⋅[σ]A, (2.15) а затем в соответствие со схемой нагружения – величину внешней нагрузки F ≤ [F].
Источник
