Расчет напряжений и построения эпюр при растяжении сжатии
Построение эпюр продольных сил – это решение статически определимой задачи. Производится для выявления картины нагрузки упругого тела. Вернее, уточнения ее схематизации.
Необходимо для определения наиболее напряженного, так называемого «опасного» сечения. Затем методами сопромата (сопротивления материалов) проводится анализ с прогнозированием перемещений элементов конструкции.
Но всему свое время. Сначала немного о терминах.
Основные понятия
Брусом (балкой) называют тело, вытянутое вдоль оси. То есть длина преобладает над шириной и высотой.

Если имеются только осевые (продольные) силы, то объект подвергается растяжению/сжатию. В этом случае в материале возникают только нормальные поперечному сечению силы противодействия и тело считают стержнем.
Статическая определимость подразумевает достаточность схемы для установления внутренних усилий противодействия. Участок – часть балки с неизменным сечением и характерной нагрузкой.
Правила построения учитывают знаки усилий. Растягивающие принимают положительными, сжимающие – отрицательными.
В системе СИ силы измеряются в ньютонах (Н). Длины в метрах (м).
Что такое эпюра продольных сил
Показывает, какой силой (в нашем предположении нормальной) загружен каждый участок. По всей длине стержня. Иначе говоря, эпюра – наглядное графическое изображение изменения нагрузки по всей длине конструкции.
Как построить эпюру продольных сил
Используется метод сечений. Балка виртуально рассекается на каждом участке и ищется противодействующая N. Ведь задача статическая.
Сопротивление рассчитывается по формуле:
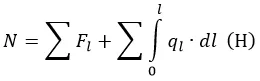
где:
Fl – действующие на участке l силы (Н);
ql – распределенные нагрузки (Н/м).
Порядок построения:
1. Рисуется схема балки и механизмов закрепления;
2. Производится разделение на участки;
3. Для каждого рассчитывается N с учетом знаков. Если у балки есть незакрепленный конец, то начинать удобнее именно с него. В противном случае считается реакция опор. И оптимальнее выбирать сечение с меньшим количеством действующих факторов:
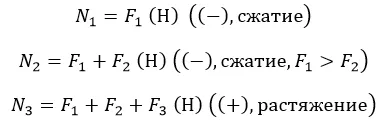
Нетрудно заметить, что последнее уравнение дает еще и реакцию опоры;
4. Параллельно оси стержня намечается база эпюры. Положительные значения масштабировано проставляются выше, отрицательные – ниже. Эпюру наглядно совмещать с расчетной схемой. Итоговый результат и промежуточные сечения показаны на рис. 1.
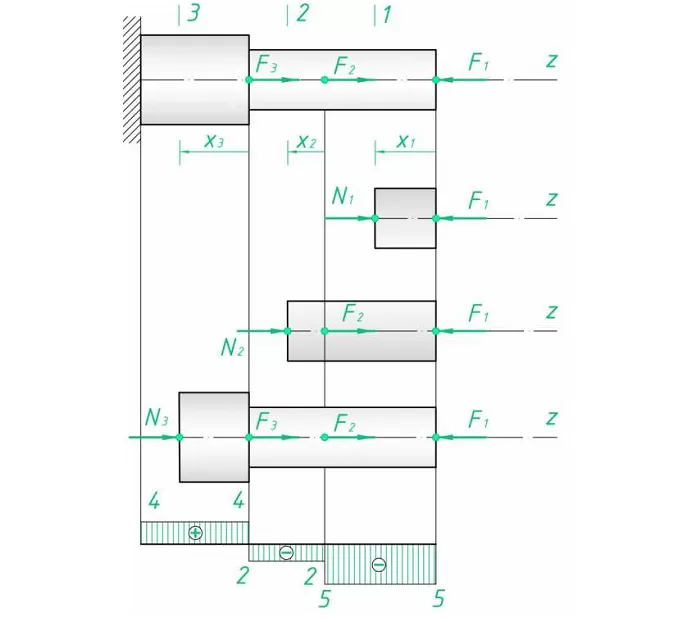
Рис. 1. Эпюра продольных сил
Рассмотрим случай:
F1 = 5 (кН);
F2 = 3 (кН);
F3 = 6 (кН).
Вычислим:
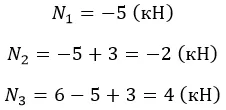
Проверить эпюру можно по скачкам: изменения происходят в точках приложения сил на их величину.
Пример построения эпюр и решения задач
Построить эпюру сил для следующего случая (рис. 2):
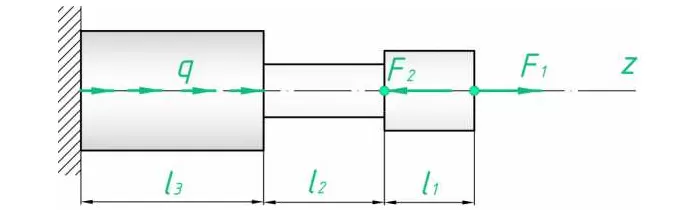
Рис. 2
Дано:
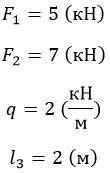
Решение.
Разбиение на участке вполне очевидно. Найдем сопротивление на выделенных:
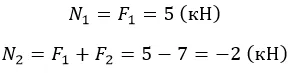
Распределенная нагрузка зависит от длины, на которой приложена. Поскольку нарастает линейно, значение N2 будет постепенно увеличиваться/уменьшаться в зависимости от знака q.
Эпюра такого вида усилия представляет собой прямоугольный треугольник с катетами l3 и ql3 (в масштабе). Поскольку распределение линейно.
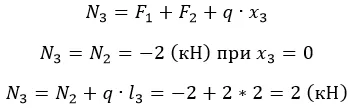
По полученным данным строим эпюру (рис. 3).
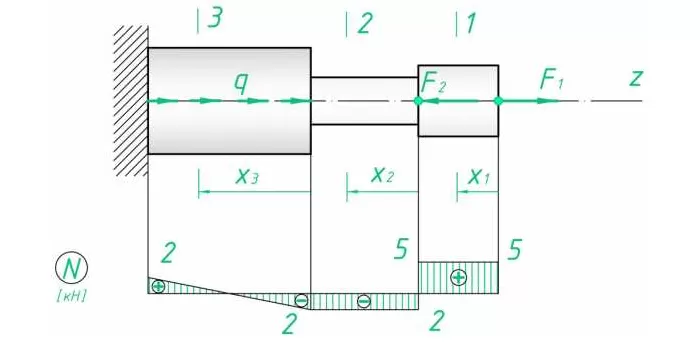
Рис. 3
Заключение
Приведенный алгоритм является предварительным этапом в расчете модели на прочность. «Слабое» место находится уже с учетом площади поперечного сечения.
В сети имеются онлайн сервисы для помощи в расчетах при вычерчивании. Но стоит ли ими пользоваться, если процедура настолько проста? Если не запутаться в знаках, конечно. Это самая распространенная ошибка.
Источник
1. На рисунке проводиться ось ОХ, совпадающая с продольной осью стержня.
2. Под рисунком стержня проводятся две базовые нулевые линии, параллельно продольной оси стержня. Одна для эпюры продольной силы Nz
Вторая базовая нулевая линия для эпюры нормальных напряжений (Мпа).
3. Стержень разбивается на участки. Для границ участков проводятся вертикальные линии в точках приложения нагрузки и изменения площади поперечного сечения вниз до пересечения с базовыми нулевыми линиями. Нумерация участков начинается со свободной стороны стержня для задачи статически определимой. Если задача статически неопределимая, то нумерация выполняется слева направо.
4. Для определения значения продольной силы используется метод сечений. В середине участка проводится сечение. Указывается направление продольной силы. Положительным считается направление продольной силы, направленной от сечения (растягивает). Значение продольной силы Nz определяется из условия равновесия отсечённой части (сумма проекций на ось ох всех действующих сил равна нулю 0).
5. Вычисляем значение нормальных напряжений.
6. Положительные значения продольной силы и нормального напряжения откладываем вверх от базовой нулевой линии, отрицательные вниз.
7. Проверяем правильность решения задачи по эпюре продольной силы. В точках, где приложена сосредоточенная сила, на эпюре должен быть скачок равный значению продольной силы.
8. Условие прочности проверяем по эпюре нормальных напряжений. Максимальные напряжения, возникающие в конструкции, не должны превышать допускаемых.
Пример №1: Построить эпюры продольной силы N и нормального напряжения σ, проверить на прочность стальной стержень, закрепленный с одной стороны (статически определимая задача). Р1 = 10кН Р2 = 15кН
Р3 =15кН
=100 Мпа; А1 = F; А2 = 2F; F = 100 мм2
Решение:
Параллельно продольной оси стержня проводим две базовые нулевые линии для продольной силы и нормального напряжения.
Разбиваем стержень на участки, начиная со свободной стороны. Проводим вниз вертикальные линии в точках приложения сил и изменения площади поперечного сечения до пересечения с нулевыми линиями. Нумерация участков начинается со свободной стороны стержня.
1 участок:
— на первом участке проводим сечение, перпендикулярное продольной оси, мысленно отбрасываем большую часть и рассматриваем меньшую часть стержня. Заменяем действие отброшенной части на оставленную продольной силой N1. Положительным считается действие от сечения (растягивает).
Рассматриваем равновесие оставленной части, проецируя действующие силы на ось ОХ:
Определяем продольную силу на первом участке:
-N1+ Р1=0 следовательно N1 = Р1=10 кН
Определяем нормальное напряжение на первом участке
2 участок:
-N2+ Р1 — Р2=0 следовательно N2 = Р1-Р2 =10-15= -5 кН
3 участок:
-N3+ Р1 — Р2=0 следовательно N3 = Р1-Р2 =10-15= -5 кН
4 участок:
-N4+ Р1 — Р2+Р3=0 следовательно N4 = Р1-Р2+Р3=10-15+15= 10 кН
Рис. 10.
Метод сечений для определения продольной силы.
Для построения эпюр продольной силы и нормального напряжения задаёмся произвольным масштабом (например: одна клеточка -5 кН и -25 мегапаскалей). Строим эпюры продольной силы и нормального напряжения, откладывая положительные значения вверх от базовой нулевой линии, отрицательные вниз.
Проверяем правильность решения задачи по эпюре продольной силы, в точке приложения сосредоточенной силы на эпюре должен быть скачок, равный действующей силе.
По эпюре нормального напряжения проверяем условие прочности максимальные напряжения должны быть меньше или равны допустимым, значит прочность обеспечена.
Рис.11.
Эпюры продольной силы N и нормального напряжения σ.
СПИСОК ЛИТЕРАТУРЫ
1. Рубашкин А.Г. Лабораторные работы по сопротивлению материалов.- М.: Высшая школа, 1961.-159с.
2. Афанасьев A.M., Марьин В.А. Лабораторный практикум по сопротивлению материалов.- М.: Наука, 1975.-284с.
3. Феодосьев В.И. Сопротивление материалов.- М.: Наука, 1979.-559с.
4. Писаренко Г.С. Сопротивление материалов.- Киев.: Высшая школа, 1973.-667с.
Источник
Пример решения задачи на растяжение и сжатие
.
Условие задачи на растяжение и сжатие
Стальной стержень (модуль Юнга кН/см2) с размерами см; см, см и площадью поперечного сечения нижнего участка см2, а верхнего – см2 нагружен внешними осевыми силами кН и кН. Построить эпюры продольных сил и нормальных напряжений . Оценить прочность стержня, если предельное напряжение (предел текучести) кН/см2, а допускаемый коэффициент запаса . Найти удлинение стержня .
Расчетная схема для задачи на растяжение и сжатие
рис 3.2
Решение пример задачи на растяжение и сжатие
Определяем значение опорной реакции , возникающей в заделке
Учитывая, что , направим опорную реакцию вниз. Тогда из уравнения равновесия находим:
кН.
Строим эпюру продольных сил
Разбиваем длину стержня на три участка. Границами участков являются сечения, в которых приложены внешние силы и (или) изменяется размер поперечного сечения стержня.
Воспользуемся методом сечений. Делаем по одному сечению в произвольном месте каждого из трех участков стержня.
Cечение 1 – 1. Отбросим (или закроем листком бумаги) верхнюю часть стержня (рис. 3.2, б). Само сечение 1 – 1 мысленно считаем неподвижным. Мы видим, что внешняя сила растягивает рассматриваемую нижнюю часть стержня. Отброшенная нами верхняя часть стержня противодействует этому растяжению. Это противодействие мы заменим внутренней продольной силой , направленной от сечения и соответствующей растяжению. Разрушения стержня не произойдет только в том случае, если возникающая в сечении 1 – 1 внутренняя продольная сила уравновесит внешнюю силу . Поэтому очевидно, что
кН.
Сечение 2 – 2. Внешняя сила растягивает рассматриваемую нами нижнюю часть стержня, а сила ее сжимает (напомним, что 2 – 2 мы мысленно считаем неподвижным). Причем, согласно условию задачи, . Чтобы уравновесить эти две силы, в сечении 2 – 2 должна возникнуть внутренняя сила , противодействующая сжатию, то есть направленная к сечению. Она равна:
кН.
Сечение 3 – 3. Отбросим теперь часть стержня, расположенную ниже этого сечения. Внутренняя продольная сила должна уравновесить внешнюю (реактивную) сжимающую силу . Поэтому она направлена к сечению и равна:
кН.
Легко убедиться в том, что полученный результат не изменится, если мы отбросим не нижнюю, а верхнюю часть стержня. В этом случае продольная сила также противодействует сжатию. Она равна:
кН.
При построении эпюры продольных сил будем пользоваться следующим правилом знаков: внутренняя продольная сила, возникающая в поперечном сечении стержня, считается положительной, если она противодействует растяжению стержня, и отрицательной, если она противодействует его сжатию. Оно вводится для того, чтобы можно было наглядно видеть, какая часть стержня испытывает деформацию растяжения, а какая часть – деформацию сжатия. Это обстоятельство может оказаться крайне важным, в частности для стержней из хрупкого материала, которые имеют разные допускаемые напряжения на растяжение и на сжатие.
Таким образом, мы установили, что в любом сечении нижнего участка стержня внутренняя продольная сила противодействует растяжению и равна кН. В любом сечении среднего и верхнего участков стержня имеет место деформация сжатия, поэтому кН.
Для построения эпюры продольных сил проводим тонкой линией ось, параллельную оси стержня z (рис. 3.2, д). Вычисленные значения продольных сил в выбранном масштабе и с учетом их знака откладываем от этой вертикальной оси. В пределах каждого из участков стержня продольная сила остается постоянной, поэтому мы как бы «заштриховываем» горизонтальными линиями соответствующий участок.
Отметим, что каждая линия «штриховки» (то есть ордината эпюры) в принятом масштабе дает значение продольной силы в соответствующем поперечном сечении стержня.
Полученную эпюру обводим жирной линией.
Анализируя полученную эпюру, мы видим, что в местах приложения внешних сил на эпюре имеет место скачкообразное изменение продольной силы на величину, равную значению соответствующей внешней силы. Причем изменение поперечного размера стержня, как это видно из рис. 3.2, д, никак не сказывается на характере эпюры .
Строим эпюру нормальных напряжений
Нормальное напряжение, возникающее в k–м поперечном сечении стержня при растяжении (сжатии), вычисляется по следующей формуле
,
где и – продольная сила и площадь k–го поперечного сечения стержня соответственно.
В первом поперечном сечении стержня нормальное напряжение равно
кН/см2,
во втором –
кН/см2,
в третьем –
кН/см2.
Строим по вычисленным значениям эпюру (рис. 3.2, е). В пределах каждого из участков стержня напряжения постоянны, то есть эпюра напряжений параллельна оси. Заметим, что в отличие от эпюры N, на эпюре «скачок» имеет место не только в местах приложения внешних сил, но и там, где происходит изменение размеров поперечного сечения стержня.
Оцениваем прочность стержня
Сопоставляем наибольшее (по модулю) нормальное напряжение , которое в нашем примере возникает во втором сечении стержня, с допускаемым напряжением . Напомним, что допускаемое напряжение представляет собой долю от предельного напряжения , то есть от напряжения, при котором начинается разрушение материала. Разрушение стали, как пластичного материала, начинается при появлении значительных остаточных деформаций. Поэтому для стали предельное напряжение равно пределу текучести: . Тогда
кН/см2.
Условие прочности имеет вид . В нашем случае
кН/см2 > кН/см2,
следовательно, прочность стержня на втором участке не обеспечена.
Таким образом, площадь поперечного сечения стержня на втором участке, равную см2, нам необходимо увеличить.
Несложный анализ показывает, что на других участках стержня условие прочности выполняется.
Из условия прочности определяем требуемую площадь поперечного сечения стержня на втором участке:
см2.
Принимаем на втором участке см2.
Вычисляем удлинение всего стержня
При переменных по длине стержня значениях продольной силы и площади поперечного сечения удлинение вычисляется по формуле
,
где E – модуль Юнга, а – длина соответствующего участка стержня.
Тогда
см.
Таким образом, длина стержня уменьшается на мм.
Задача по сопромату на растяжение и сжатие для самостоятельного решения
Условие задачи на растяжение и сжатие
Стальной стержень (модуль Юнга кН/см2) находится под действием внешних осевых сил и (рис. 3.1). Построить эпюры продольных сил и нормальных напряжений . Оценить прочность стержня, если предельное напряжение (предел текучести) кН/см2, а допускаемый коэффициент запаса . Найти удлинение стержня .
Схемы для задачи на растяжение и сжатие
Исходные данные к задаче на растяжение и сжатие
Номер схемы | F, см2 | a, м | b, м | c, м | P, кН |
1 | 2,0 | 1,2 | 1,4 | 1,6 | 11 |
2 | 2,2 | 1,4 | 1,6 | 1,4 | 12 |
3 | 2,4 | 1,8 | 1,6 | 1,2 | 13 |
4 | 2,6 | 1,6 | 2,0 | 1,0 | 14 |
5 | 2,8 | 2,0 | 1,8 | 1,2 | 15 |
6 | 3,0 | 2,2 | 1,6 | 1,4 | 16 |
7 | 3,2 | 2,4 | 1,4 | 1,6 | 17 |
8 | 3,4 | 2,6 | 1,2 | 1,8 | 18 |
9 | 3,6 | 2,8 | 1,0 | 1,4 | 19 |
3,8 | 2,4 | 1,6 | 1,2 | 20 |
Источник
Сопротивление материалов
Растяжение и сжатие
Напряжения и характер деформаций при растяжении и сжатии
Растяжением или сжатием называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только продольная сила.
Брусья с прямолинейной осью, работающие на растяжение или сжатие, часто называются стержнями.
Рассмотрим невесомый, защемленный левым концом прямой брус, вдоль оси которого действуют активные силы F и 2F (рис. 1).
Части бруса постоянного сечения, заключенные между поперечными плоскостями (сечениями), в которых приложены одинаковые внешние силы (нагрузки или реакции связей) будем называть участками. Т. е. участок — это однородный кусок бруса и по форме, и по нагрузкам, и по площади сечения.

Изображенный на рис. 1 брус состоит из двух участков – от защемленного конца до места приложения силы F, и от силы F до свободного конца, к которому приложена сила 2F.
Применим метод сечений и определим продольные внутренние силы N1 и N2 на этих участках.
Сначала рассечем брус плоскостью 1-1 и мысленно отбросим правую часть бруса, заменив ее эквивалентными внутренними и внешними силами.
Применим уравнения равновесия для этой части бруса:
∑ Z = 0, следовательно: 2F – F – N1 = 0, откуда N1 = 2F – F = F.
Очевидно, что для сохранения равновесия части бруса достаточно приложить продольную силу. Нетрудно понять, что на втором участке бруса продольная сила в сечении 2-2 будет иметь другое значение: N2 = 2F.
Таким образом, продольная сила в поперечном сечении бруса равна алгебраической сумме внешних сил, расположенных по одну сторону от рассматриваемого сечения и в пределах каждого участка имеет одинаковое значение.
Последнее утверждение не совсем справедливо, поскольку в местах приложения внешних сил внутренние силы распределяются по сложным закономерностям, но с учетом рассмотренного ранее принципа смягчения граничных условий (принципа Сен-Венана), мы допускаем некоторую условную погрешность, незначительно влияющую на итоговый результат расчета.
При определении величины продольной силы алгебраическим сложением внешних сил следует обращать внимание на знаки (векторные значения) этих сил. При расчетах в сопромате обычно принимают растягивающие нагрузки (направленные от сечения) положительными, а сжимающие – отрицательными.
При изучении ряда деформаций мы будем мысленно представлять брусья состоящими из бесконечного количества волокон, расположенных параллельно оси бруса, и предполагать, что при деформации растяжения и сжатия эти волокна не надавливают друг на друга (гипотеза о не надавливании волокон).
Чтобы понять характер напряжений и деформаций, возникающих в сжимаемом или растягиваемом брусе, представим себе прямой брус из резины, на котором нанесена сетка из продольных и поперечных линий. Если такой брус подвергнуть деформации растяжения, можно заметить, что:
- поперечные линии на брусе остаются ровными и перпендикулярными оси бруса, а расстояния между ними увеличатся;
- продольные линии останутся прямыми, а расстояния между ними уменьшатся.
Из этого эксперимента следует, что при растяжении справедлива гипотеза плоских сечений (гипотеза Бернулли), и, следовательно, все волокна бруса удлинятся на одну и ту же величину. Все это позволяет сделать вывод, что при растяжении и сжатии в поперечных сечениях бруса возникают только нормальные напряжения, равномерно распределенные по сечению. Эти напряжения можно определить по формуле:
σ = N / А,
где N – продольная сила, А – площадь поперечного сечения бруса.
Очевидно, что при растяжении и сжатии форма сечения бруса на величину напряжений не влияет.
Для наглядного изображения распределения продольных сил и нормальных напряжений вдоль оси бруса строят графики, называемые эпюрами (от французского «epure» — чертеж, график) , при этом на эпюрах при построении учитывают знаки (векторные значения) продольных сил и напряжений.

Для ступенчатого бруса, к которому приложены сжимающая 2F и растягивающая 3F силы на рис. 2 показаны соответствующие эпюры продольных сил N и нормальных напряжений σ.
Порядок построения эпюр таков: сначала под чертежом бруса проводят прямую линию, параллельную оси бруса (эта линия условно представляет брус), затем напротив каждого сечения бруса откладывают по этой линии величину силовых факторов: для положительных – вверх, для отрицательных — вниз. Масштаб при этом выбирается произвольный. Разумеется, перед построением эпюры необходимо подсчитать величину силовых факторов (сил, моментов сил или напряжений) в каждом участке бруса.
На полученном графике в кружках указываются знаки силовых факторов по участкам, на наружных углах ступенчатых переходов ставятся числовые значения этих силовых факторов, а вся площадь графика заштриховывается тонкими линиями, перпендикулярными оси.
Слева от оси эпюры указывается, какой силовой фактор на ней представлен.
По эпюрам, представленным на рис. 2 можно заметить, что в местах приложения внешних нагрузок и реакций внутренние силовые факторы изменяются скачкообразно (принцип Сен-Венана).
Визуальное исследование эпюры позволяет определить критические участки бруса, находящиеся в наиболее напряженном состоянии. Так, по представленным на рис. 2 эпюрам напряжений, возникающих в брусе, можно определить, что критическим является 2-й участок, поскольку здесь возникает наибольшее напряжение (по эпюре видно, что это напряжение сжатия, т. к. оно имеет отрицательное значение).
Кроме того, эпюра любого силового фактора позволяет (без применения лишних расчетов) определить силу или момент, действующие на брус со стороны, например, заделки, поскольку после построения эпюры со стороны свободного конца бруса эти силовые факторы отобразятся графически, без вычислений.
Ниже размещен видеоролик, в котором подробно объясняется порядок построения эпюр продольных сил и напряжений, возникающих в брусе при растяжении и сжатии, а также выводы, которые можно сделать на основе визуального анализа графиков.
Видеоурок ведет преподаватель ГОУ СПО «Нижнетагильский горно-металлургический колледж» Чирков А. С.
***
Материалы раздела «Растяжение и сжатие»:
- Деформации при растяжении и сжатии. Потенциальная энергия деформации растяжения.
- Расчеты на прочность при растяжении и сжатии. Статически неопределимые задачи.
- Закон Гука
Смятие
Правильные ответы на вопросы Теста № 4
№ вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Правильный вариант ответа | 1 | 1 | 2 | 1 | 3 | 2 | 2 | 1 | 3 | 1 |
Источник
