Расчет на растяжение калькулятор
+- мdA
площадь сечения стержняZB м м м м м м м м м м м м м м м м м м м м м м м м м м м м мL=2(м)N[кН]
Продольная сила N,кН0σ [МПа]
Напряжения ,МПа0δ [мм]
Перемещения характерных сечений ,мм0
Модуль упругости E=
ГПа (сталь)
Выбрать из таблицы
Длина стержня l=
м.
Площадь A= = 0.0004 м2
Выбрать тип сечения исходя из условий задачи
Круг
Квадрат
Прямоугольник
Шестигранник
Кольцевое сечение (труба)
Площадь сечения в см2:
A = π · d2/4
= 3.14·(d·0.1)2/4 =
[см2]
Масса 1 м профиля, [кг]:
m = ρ·A·L =
7850· A ·1/10000 = [кг]
ДСТУ 4738:2007/ГОСТ 2590-2006 Прокат сортовой стальной горячекатаный круглый.
(При вычислении массы 1 м проката плотность стали принята равной 7850 кг/м3)
Выбрать диаметр из сортамента:
| Диаметр d, мм | |||||||||||||||||||
| 5 | 5.5 | 6 | 6.3 | 6.5 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 |
| 42 | 43 | 44 | 45 | 46 | 47 | 48 | 50 | 52 | 53 | 54 | 55 | 56 | 58 | 60 | 62 | 63 | 65 | 67 | 68 |
| 70 | 72 | 73 | 75 | 78 | 80 | 82 | 85 | 87 | 90 | 92 | 95 | 97 | 100 | 105 | 110 | 115 | 120 | 125 | 130 |
| 135 | 140 | 145 | 150 | 155 | 160 | 165 | 170 | 175 | 180 | 185 | 190 | 195 | 200 | 210 | 220 | 230 | 240 | 250 | 260 |
| 270 | |||||||||||||||||||
ДСТУ ГОСТ 1535:2007/ГОСТ 1535-2006 Прутки медные
(При вычислении массы 1 м проката плотность меди принята равной 8900 кг/м3)
Выбрать диаметр из сортамента:
| Номинальный диаметр d, мм | |||||||||||||||||||
| 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 24 | 25 | 27 | 28 | 30 | 32 | 33 | 35 | 36 | 38 | 40 | 41 | 45 | 46 | 50 | ||
| Номинальный диаметр d, мм | |||||||||||||||||||
| 20 | 22 | 25 | 28 | 30 | 32 | 35 | 38 | 40 | 42 | 45 | 48 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 |
| 90 | 95 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | |||||||||
ДСТУ ГОСТ 2060:2007/ГОСТ 2060-2006 Прутки латунные
(При вычислении массы 1 м проката плотность латуни принята равной 8500 кг/м3)
Выбрать диаметр из сортамента:
| Номинальный диаметр d, мм | |||||||||||||||||||
| 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | 9 | 9.5 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 30 | 32 | 35 | 36 | 38 | 40 | 41 |
| 42 | 45 | 46 | 48 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 | 110 | 120 | 130 | 140 | 150 |
| 160 | 170 | 180 | |||||||||||||||||
ГОСТ 21488-97 Прутки прессованные из алюминия и алюминиевых сплавов
(При вычислении массы 1 м проката плотность алюминия принята равной 2700 кг/м3)
Выбрать диаметр из сортамента:
| Номинальный диаметр d, мм | |||||||||||||||||||
| 8 | 10 | 12 | 14 | 16 | 18 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 90 |
| 100 | 110 | 120 | 130 | 140 | 150 | 160 | 180 | 200 | 250 | 300 | 350 | 400 | |||||||
ГОСТ 26492-85 Прутки катаные из титана и титановых сплавов
(При вычислении массы 1 м проката плотность титана принята равной 4500 кг/м3)
Выбрать диаметр из сортамента:
| Номинальный диаметр d, мм | |||||||||||||||||||
| 10 | 12 | 14 | 16 | 18 | 20 | 22 | 25 | 28 | 30 | 32 | 35 | 38 | 40 | 42 | 45 | 48 | 50 | 52 | 55 |
| 60 | 65 | 70 | 75 | 80 | 85 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | |||||||
ТУ 48-19-39-85 Прутки вольфрамовые
(При вычислении массы 1 м проката плотность титана принята равной 19300 кг/м3)
Выбрать диаметр из сортамента:
| Номинальный диаметр d, мм | |||||||||||||||||||
| 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | 9 | 9.5 | 10 | 10.5 | 11 | 11.5 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | |||||||||||||||
ТУ 48-19-247-87 Прутки молибденовые диаметром от 16 до 125 мм
(При вычислении массы 1 м проката плотность молибдена принята равной 10188 кг/м3)
Выбрать диаметр из сортамента:
| Номинальный диаметр d, мм | |||||||||||||||||||
| 16 | 17 | 18 | 19 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 | 42 | 44 | 46 | 48 | 50 |
| 52 | 54 | 56 | 58 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 | 105 | 110 | 115 | 120 | 125 | ||
ГОСТ 13083-2016 Прутки из никеля и кремнистого никеля
(При вычислении массы 1 м проката плотность никеля принята равной 8900 кг/м3)
Выбрать диаметр из сортамента:
| Номинальный диаметр d, мм | |||||||||||||||||||
| 5 | 5.5 | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | 9 | 9.5 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 30 | 32 | 34 | 36 | 38 | 40 | |||||
| Номинальный диаметр d, мм | |||||||||||||||||||
| 42 | 45 | 48 | 50 | 55 | 60 | 70 | 80 | 90 | |||||||||||
a
Площадь сечения в см2:
A = a2 = (a·0.1)2 =
[см2]
Масса 1 м профиля, [кг]:
m = ρ·A·L =
7850· A ·1/10000 = [кг]
(При вычислении массы 1 м проката плотность стали принята равной 7850 кг/м3)
ДСТУ 4746:2007/ГОСТ 2591-2006 Прокат сортовой стальной горячекатаный квадратный.
Выбрать размер из сортамента:
DAs
D=s/2 + (2A)/(πs)
Толщина стенки трубы s=
мм
Нормальные линейные размеры (диаметры, длины, высоты и др.) должны выбираться в соответствии с таблицей
(размеры в мм)
Выбрать размер из таблицы:
| Ra5 | |||||||||||||||||||
| 0,1 | 0,4 | 0,63 | 1,0 | 1,6 | 2,5 | 4,0 | 6,3 | 10,0 | 16,0 | 25 | 40 | 63 | 100 | 160 | 250 | 400 | 630 | 1000 | 1600 |
| Ra10 | |||||||||||||||||||||||||||||
| 0,1 | 0,2 | 0,4 | 0,5 | 0,63 | 0,8 | 1,0 | 1,2 | 1,6 | 2,0 | 2,5 | 3,2 | 4,0 | 5,0 | 6,3 | 8,0 | 10 | 12 | 16 | 20 | 25 | 32 | 40 | 50 | 63 | 80 | 100 | 125 | 160 | 200 |
| 250 | 320 | 400 | 500 | 630 | 800 | 1000 | 1250 | 1600 | 2000 | ||||||||||||||||||||
| Ra20 | |||||||||||||||||||||||||||||
| 0,1 | 0,2 | 0,4 | 0,5 | 0,63 | 0,71 | 0,8 | 0,9 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 | 2,5 | 2,8 | 3,2 | 3,6 | 4,0 | 4,5 | 5,0 | 5,6 | 6,3 | 7,1 | 8,0 | 9,0 | 10 | 11 | 12 |
| 14 | 16 | 20 | 22 | 25 | 28 | 32 | 36 | 40 | 45 | 50 | 56 | 63 | 71 | 80 | 90 | 100 | 110 | 125 | 140 | 160 | 180 | 200 | 220 | 250 | 280 | 320 | 360 | 400 | 450 |
| 500 | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 | 1800 | 2000 | |||||||||||||||||
| Ra40 | |||||||||||||||||||||||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,63 | 0,71 | 0,8 | 0,9 | 1,0 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 | 2,1 | 2,2 | 2,4 | 2,5 | 2,6 | 2,8 | 3,0 | 3,2 | 3,4 | 3,6 | 3,8 |
| 4,0 | 4,2 | 4,5 | 4,8 | 5,0 | 5,3 | 5,6 | 6,0 | 6,3 | 6,7 | 7,1 | 7,5 | 8,0 | 8,5 | 9,0 | 9,5 | 10,0 | 10,5 | 11,0 | 11,5 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 24 | 25 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 | 42 | 45 | 48 | 50 | 53 | 56 | 60 | 63 | 67 | 71 | 75 | 80 | 85 | 90 | 95 | 100 | 105 | 110 | 120 |
| 125 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 | 210 | 220 | 240 | 250 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 | 420 | 450 | 480 | 500 | 530 | 560 | 600 | 630 | 670 |
| 710 | 750 | 800 | 850 | 900 | 950 | 1000 | 1060 | 1120 | 1180 | 1250 | 1320 | 1400 | 1500 | 1600 | 1700 | 1800 | 2000 | ||||||||||||
| Дополнительные размеры | |||||||||||||||||||||||||||||
| 2,3 | 2,7 | 2,9 | 3,1 | 3,3 | 3,5 | 3,7 | 3,9 | 4,1 | 4,4 | 4,6 | 4,9 | 5,2 | 5,5 | 5,8 | 6,2 | 6,5 | 7,0 | 7,3 | 7,8 | 8,2 | 8,8 | 9,2 | 9,8 | 10,2 | 10,8 | 11,2 | 11,8 | 12,5 | |
| 13,5 | 14,5 | 15,5 | 16,5 | 17,5 | 18,5 | 19,5 | 20,5 | 21,5 | 23 | 27 | 29 | 31 | 33 | 35 | 37 | 39 | 41 | 52 | 55 | 58 | 65 | 70 | 73 | 78 | 82 | 88 | 92 | 98 | |
| 102 | 108 | 112 | 115 | 118 | 135 | 145 | 155 | 165 | 175 | 185 | 195 | 205 | 215 | 230 | 270 | 290 | 310 | 315 | 330 | 350 | 370 | 390 | 410 | 440 | 460 | 490 | 515 | 545 | |
| 580 | 615 | 650 | 690 | 730 | 775 | 825 | 875 | 925 | 975 | 1030 | 1090 | 1150 | 1220 | 1280 | 1360 | 1450 | 1550 | 1650 | 1750 | 1850 | 1950 | ||||||||
1) При выборе размеров предпочтение должно отдаваться рядам с более крупной градацией
(ряд Ra5 – ряду Ra10, ряд Ra10 – ряду Ra20, ряд Ra20 – ряду Ra40).
2) Дополнительные размеры допускается применять лишь в отдельных, технически обоснованных случаях.
Кол-во сил F, действующих на стержень:
Длина — расстояние прилагаемой нагрузки от заделки:
Источник
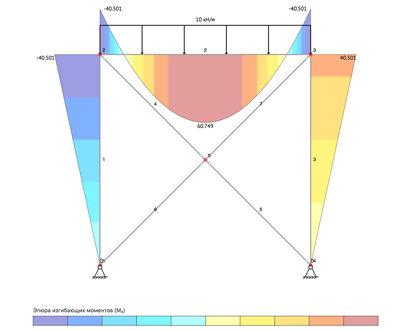
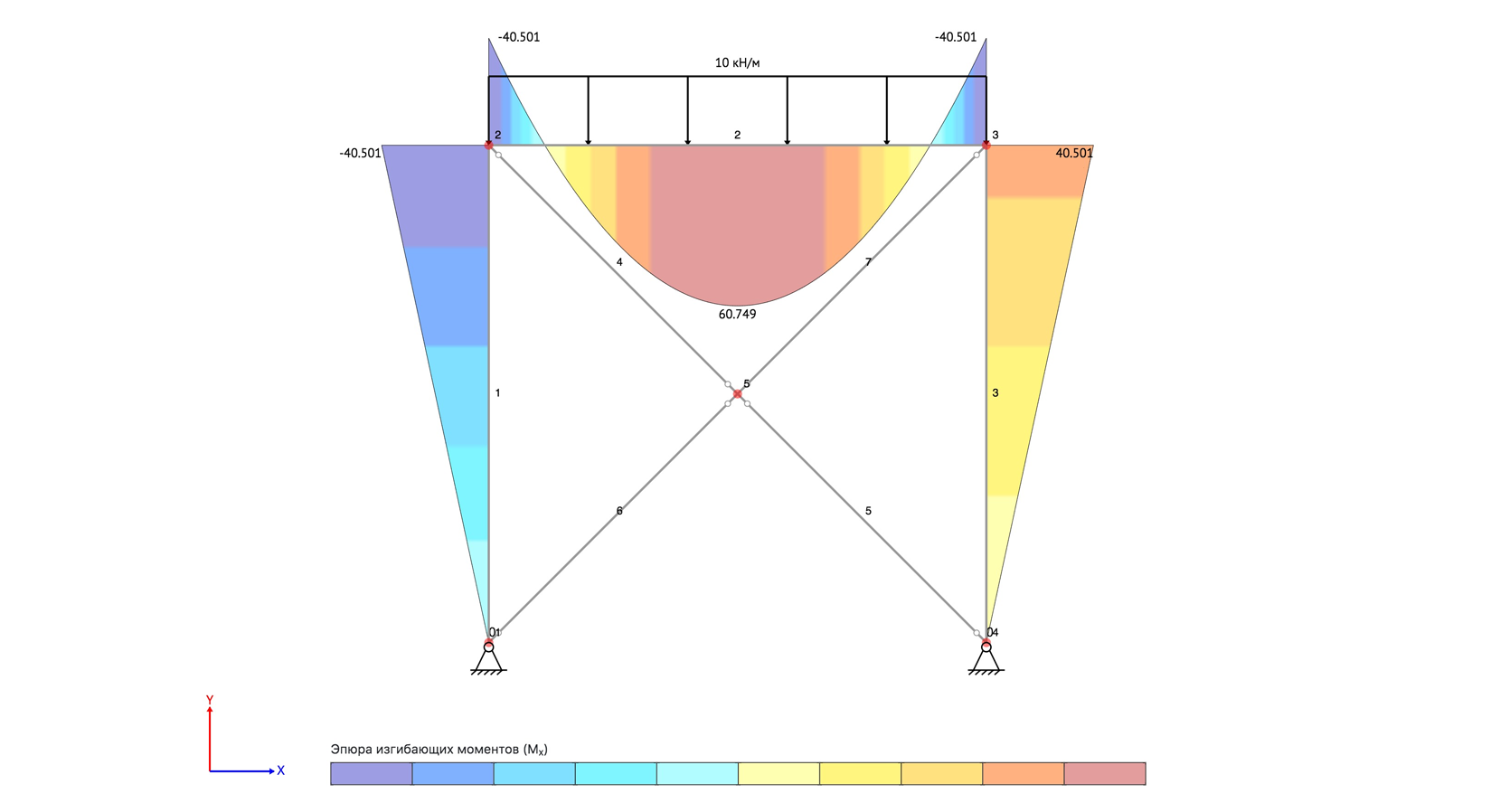
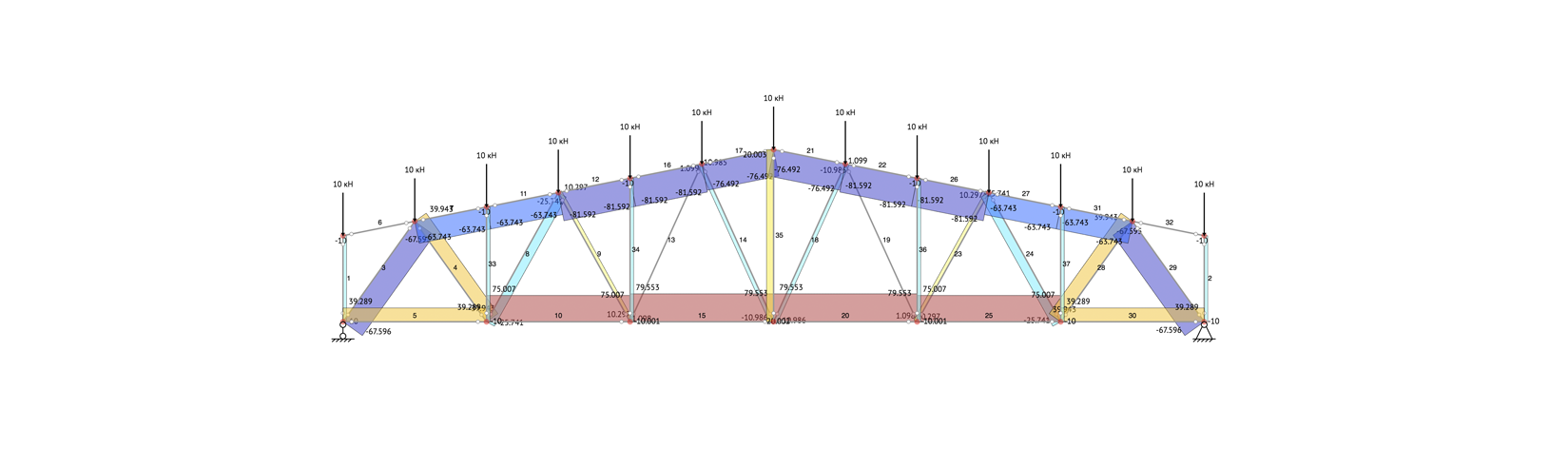
Расчет рамы/фермы
Расчет
статически-неопределимых систем
Расчет
методом конечных элементов
Построение
эпюры моментов (М)
Построение
эпюры поперечных сил (Q)
Построение
эпюры продольных сил (N)
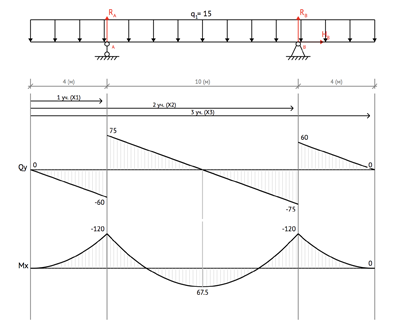
Построение
эпюры моментов (М)
Построение
эпюры поперечных сил (Q)
Построение
эпюры продольных сил (N)
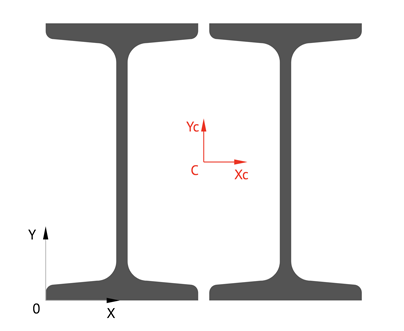
Расчет
геометрических характеристик поперечного сечения
Определение
центра тяжести, моментов инерции, моментов сопротивления
Формирование
подробного отчета

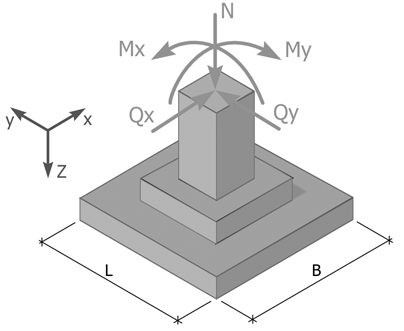
Расчет
столбчатого фундамента
Расчет
ленточного фундамента
Формирование
подробного отчета
Расчет
статически-неопределимых систем
Расчет
методом конечных элементов
Построение
эпюры моментов (М)
Построение
эпюры поперечных сил (Q)
Построение
эпюры продольных сил (N)
Источник
Нагружение стержня, при котором из всех внутренних силовых факторов в его поперечных сечениях не равен нулю только момент, вектор которого направлен вдоль оси стержня, называется кручением. Стержни, работающие в таких условиях, называются валами.
При кручении цилиндрического вала, в его поперечных сечениях возникают только касательные напряжения, и это напряженное состояние называется “чистый сдвиг”. При этом, поперечные сечения вала остаются плоскими и не меняют своего размера в радиальном направлении. Так же не меняются расстояния между поперечными сечениями, но при этом они поворачиваются друг относительно друга на некоторый угол φ.
В общем случае, максимальные касательные напряжения возникают у края поперечного сечения, за исключением наружных углов, в которых касательные напряжения равны нулю. Стержень не круглого поперечного сечения испытывает депланации – точки его сечения выходят из плоскости и перемещаются вдоль оси стержня в различных направлениях.
Онлайн расчеты, представленные в данном разделе, рассматривают кручение круглого вала сплошного сечения, кручение круглого вала с отверстием, выполненным с эксцентриситетом, треугольное, прямоугольное сечение, а так же кручение стержней стандартных сечений – уголка, двутавра и швеллера.
Расчет кручения вала круглого сечения
Расчет максимальных касательных напряжений и угла поворота при кручении вала сплошного круглого сечения.
Исходные данные:
D – наружный диаметр вала, в миллиметрах;
L – длина вала, в миллиметрах;
Т – крутящий момент на валу, в ньютонах × метр;
ν – коэффициент Пуассона;
Е – модуль упругости материала вала, в паскалях.
КРУЧЕНИЕ ВАЛА КРУГЛОГО СЕЧЕНИЯ
Наружный диаметр D, мм
Длина вала L, мм
Крутящий момент на валу Т, Н*м
Коэффициент Пуассона ν
Модуль упругости Е, Па
Максимальное касательное напряжение τ, МПа
Угол поворота φ, град
Максимальное касательное напряжение:
τ = 2Т/π×r3;
Угол поворота:
φ = 2T×L / (π×r4 × G),где
G – модуль сдвига.
Расчет кручения вала круглого сечения с отверстием
Расчет максимальных касательных напряжений и угла поворота при кручении вала круглого сечения c отверстием.
Исходные данные:
D – наружный диаметр вала, в миллиметрах;
d – внутренний диаметр вала, в миллиметрах;
e – эксцентриситет отверстия, в миллиметрах;
L – длина вала, в миллиметрах;
Т – крутящий момент на валу, в ньютонах × метр;
ν – коэффициент Пуассона;
Е – модуль упругости материала вала, в паскалях.
КРУЧЕНИЕ ВАЛА С ОТВЕРСТИЕМ
Наружный диаметр D, мм
Внутренний диаметр d, мм
Эксцентриситет e, мм
Длина вала L, мм
Крутящий момент на валу Т, Н*м
Коэффициент Пуассона ν
Модуль упругости Е, Па
Максимальное касательное напряжение τ, МПа
Угол поворота φ, град
Ref 8 Table 10.1
Расчет кручения стержня прямоугольного сечения
Расчет максимальных касательных напряжений и угла поворота при кручении стержня прямоугольного сечения.
Исходные данные:
a – длина сечения стержня, в миллиметрах;
b – высота сечения стержня, в миллиметрах;
L – длина стержня, в миллиметрах;
Т – крутящий момент, в ньютонах × метр;
ν – коэффициент Пуассона;
Е – модуль упругости материала стержня, в паскалях.
КРУЧЕНИЕ ПРЯМОУГОЛЬНОГО СТЕРЖНЯ
Длина сечения a, мм
Высота сечения b, мм
Длина стержня L, мм
Крутящий момент Т, Н*м
Коэффициент Пуассона ν
Модуль упругости Е, Па
Максимальное касательное напряжение τ, МПа
Угол поворота φ, град
Ref 8 Table 10.1
Расчет кручения стержня треугольного сечения
Расчет максимальных касательных напряжений и угла поворота при кручении стержня треугольного равнобедренного сечения.
Исходные данные:
a – длина основания сечения стержня, в миллиметрах;
b – длина боковой стороны сечения стержня, в миллиметрах;
L – длина стержня, в миллиметрах;
Т – крутящий момент, в ньютонах × метр;
ν – коэффициент Пуассона;
Е – модуль упругости материала стержня, в паскалях.
КРУЧЕНИЕ СТЕРЖНЯ ТРЕУГОЛЬНОГО СЕЧЕНИЯ
Длина основания a, мм
Длина боковой стороны b, мм
Длина стержня L, мм
Крутящий момент Т, Н*м
Коэффициент Пуассона ν
Модуль упругости Е, Па
Максимальное касательное напряжение τ, МПа
Угол поворота φ, град
Ref 8 Table 10.1
Расчет кручения стержня прямоугольного сечения с тонкой стенкой
Расчет максимальных касательных напряжений (τ на стороне b иτ1 на стороне a) и угла поворота при кручении стержня прямоугольного сечения с тонкой стенкой.
Исходные данные:
a – длина сечения сечения стержня, в миллиметрах;
b – высота сечения стержня, в миллиметрах;
s – толщина стенки стержня на стороне b, в миллиметрах;
s1 – толщина стенки стержня на стороне a, в миллиметрах;
L – длина стержня, в миллиметрах;
Т – крутящий момент, в ньютонах × метр;
ν – коэффициент Пуассона;
Е – модуль упругости материала стержня, в паскалях.
КРУЧЕНИЕ ТОНКОСТЕННОГО ПРЯМОУГОЛЬНОГО СТЕРЖНЯ
Длина сечения a, мм
Высота сечения b, мм
Толщина сечения s, мм
Толщина сечения s1, мм
Длина балки L, мм
Крутящий момент Т, Н*м
Коэффициент Пуассона ν
Модуль упругости Е, Па
Максимальное касательное напряжение τ, МПа
Максимальное касательное напряжение τ1, МПа
Угол поворота φ, град
Ref 8 Table 10.1
Расчет кручения уголка
Расчет максимальных касательных напряжений и угла поворота при кручении уголка.
Стержни таких поперечных сечений как уголок, швеллер, двутавр никогда не предназначаются для передачи крутящего момента, но в некоторых случаях могут испытывать крутящие нагрузки вследствие особенностей общей геометрии конструкции.
Исходные данные:
a – высота уголка, в миллиметрах;
b – ширина уголка, в миллиметрах;
b, d – толщина полок уголка, в миллиметрах;
r – радиус закругления полок, в миллиметрах;
L – длина стержня, в миллиметрах;
Т – крутящий момент, в ньютонах × метр;
ν – коэффициент Пуассона;
Е – модуль упругости материала стержня, в паскалях.
КРУЧЕНИЕ УГОЛКА
Высота уголка а, мм
Ширина уголка с, мм
Толщина полки b, мм
Толщина полки d, мм
Радиус закругления r, мм
Длина балки L, мм
Крутящий момент Т, Н*м
Коэффициент Пуассона ν
Модуль упругости Е, Па
Максимальное касательное напряжение τ, МПа
Угол поворота φ, град
Ref 8 Table 10.1
Расчет кручения швеллера
Расчет максимальных касательных напряжений и угла поворота при кручении швеллера.
Исходные данные:
a – ширина швеллера, в миллиметрах;
с – высота швеллера, в миллиметрах;
b – толщина полки, в миллиметрах;
d – толщина стенки, в миллиметрах;
r – внутренний радиус закругления, в миллиметрах;
L – длина стержня, в миллиметрах;
Т – крутящий момент, в ньютонах × метр;
ν – коэффициент Пуассона;
Е – модуль упругости материала стержня, в паскалях.
КРУЧЕНИЕ ШВЕЛЛЕРА
Ширина швеллера а, мм
Высота швеллера с, мм
Толщина полки b, мм
Толщина полки d, мм
Радиус закругления r, мм
Длина балки L, мм
Крутящий момент на Т, Н*м
Коэффициент Пуассона ν
Модуль упругости Е, Па
Максимальное касательное напряжение τ, МПа
Угол поворота φ, град
Ref 8 Table 10.1
Расчет кручения двутавра
Расчет максимальных касательных напряжений и угла поворота при кручении двутавра.
Исходные данные:
a – ширина двутавра, в миллиметрах;
с – высота двутавра, в миллиметрах;
b – толщина полки, в миллиметрах;
d – толщина стенки, в миллиметрах;
r – внутренний радиус закругления, в миллиметрах;
L – длина стержня, в миллиметрах;
Т – крутящий момент, в ньютонах × метр;
ν – коэффициент Пуассона;
Е – модуль упругости материала стержня, в паскалях.
КРУЧЕНИЕ ДВУТАВРА
Ширина двутавра а, мм
Высота двутавра с, мм
Толщина полки b, мм
Толщина полки d, мм
Радиус закругления r, мм
Длина балки L, мм
Крутящий момент Т, Н*м
Коэффициент Пуассона ν
Модуль упругости Е, Па
Максимальное касательное напряжение τ, МПа
Угол поворота φ, град
©ООО”Кайтек”, 2020. Любое использование либо копирование материалов или подборки материалов сайта, может осуществляться лишь с разрешения автора (правообладателя) и только при наличии ссылки на сайт www.caetec.ru
Источник
