Расчет на прочность при растяжении и сжатии колонн

На чтение 4 мин. Просмотров 5.1k. Обновлено 25 ноября, 2020
Калькулятор предназначен для расчёта центрально-нагруженных стоек (колонн) из стальных труб круглого, квадратного и прямоугольного сечения.
При проектировании строительных конструкций необходимо принимать схемы, обеспечивающие прочность, устойчивость и пространственную неизменяемость сооружения в целом, а также его отдельных элементов при монтаже и эксплуатации. Поэтому стойку,находящуюся под действием сжимающей её нагрузки необходимо проверять:
- На прочность;
- Устойчивость;
- Допустимую гибкость.
Укажите форму поперечного сечения трубы
| Круглая | Квадратная | Прямоугольная |
 | ||
| Заделка-консоль | Заделка-заделка | Заделка-шарнир | Шарнир-шарнир |
 | |||
| Материал труб1 | Вид и назначение стоек (колонн) |
| Если Вашего материала нет в таблице, но Вам известно расчётное сопротивление этого материала, ведите его значение в это поле (кг/см2): | |
Введите параметры для расчёта
| Длина стойки L, м | Размер D или A, мм | Размер B, мм |
| Толщина S, мм | Нагрузка P, кг |
Логика расчета на прочность и устойчивость стоек (колонн) из стальных труб
Согласно Актуализированной редакция СНиП II-23-81 (CП16.13330,2011) расчет на прочность элементов из стали при центральном растяжении или сжатии силой P следует выполнять по формуле:
P / Fp * Ry * Yc <= 1, где:
- P – действующая нагрузка,
- Fp – плошадь поперечного сечения стойки,
- Ry – расчётное сопротивление материала (стали стойки), выбирается по таблице В5 Приложения “В” того же СНиПа;
- Yc – коэффициент условий работы по таблице 1 СНиПа (0.9-1.1).В соответствии с примечанием к этой таблице (пункт 5) в калькуляторе принято Yc=1.
Проверку на устойчивость элементов сплошного сечения при центральном сжатии силой P следует выполнять по формуле:
P / Fi * Fp * Ry * Yc <= 1, где Fi – коэффициент продольного изгиба центрально – сжатых элементов. Коэффициент Fi введён в расчёт в качестве компенсации возможности некоторой не прямолинейности стойки, недостаточной жесткости её крепления и неточности в приложении нагрузки относительно оси стойки. Значение Fi зависит от марки стали и гибкости колонны и часто берётся из таблицы 72 СНиП II-23-81 1990г. Исходя из гибкости стойки и расчётного сопротивления выбранной стали сжатию, растяжению и изгибу. Это несколько упрощает и огрубляет расчёт, так как СНиП II-23-81* предусматривает специальные формулы для определения Fi.
Гибкость (Lambda) – некоторая величина, характеризующая свойства рассматриваемого стержня в зависимости от его длины и параметров поперечного сечения, в частности радиуса инерции: Lambda = Lr / i;
- здесь Lr – расчётная длина стержня,
- i – радиус инерции поперечного сечения стержня (стойки,колонны).
Радиус инерции сечения i равен корню квадратному из выражения I / Fp, где I – момент инерции сечения, Fp – его площадь.
Lr (расчётная длина) определяется как MuL;
здесь L – длина стойки, а Mu – коэфф., зависящий от схемы её крепления:
- “заделка-консоль”(свободный конец)-Mu=2;
- “заделка-заделка”-Mu=0.5;
- заделка-шарнир”-Mu=0.7;
- “шарнир-шарнир”-Mu=1.
Следует иметь ввиду,что при наличии у формы поперечного сечения 2-ух радиусов инерции (например, у прямоугольника), при расчёте Lambda используется меньший. Кроме того,сама Lambda (гибкость стойки), рассчитанная по формуле Lambda = Lr / i не должна превышать 220-ти в соответствии с табл. 19.СНиП II-23-81*; там же содержатся ограничения на предельную гибкость центрально-сжатых стержней.
Для их использования необходимо сделать выбор в таблице калькулятора “Вид, назначение стоек…”. Предельная гибкость стоек, кроме их геометрических параметров, зависит также от коэфф. продольного изгиба (Fi), действующей нагрузки(P), расчётного сопротивления материала стойки (Ry) и условий её работы (Yc).
Оцените автора
( 3 оценки, среднее 3.67 из 5 )
Источник
Колонна — это вертикальный элемент несущей конструкции здания, которая передает нагрузки от вышерасположенных конструкций на фундамент.
При расчете стальных колонн необходимо руководствоваться СП 16.13330 «Стальные конструкции».
Для стальной колонны обычно используют двутавр, трубу, квадратный профиль, составное сечение из швеллеров, уголков, листов.
Для центрально-сжатых колонн оптимально использовать трубу или квадратный профиль — они экономны по массе металла и имеют красивый эстетический вид, однако внутренние полости нельзя окрасить, поэтому данный профиль должен быть герметично.
Широко распространено применение широкополочного двутавра для колонн — при защемлении колонны в одной плоскости данный вид профиля оптимален.
Большое значение влияет способ закрепления колонны в фундаменте. Колонна может иметь шарнирное крепление, жесткое в одной плоскости и шарнирное в другой или жесткое в 2-х плоскостях. Выбор крепления зависит от конструктива здания и имеет больше значение при расчете т.к. от способа крепления зависит расчетная длина колонны.
Также необходимо учитывать способ крепления прогонов, стеновых панелей, балки или фермы на колонну, если нагрузка передается сбоку колонны, то необходимо учитывать эксцентриситет.
При защемлении колонны в фундаменте и жестком креплении балки к колонне расчетная длина равна 0,5l, однако в расчете обычно считают 0,7l т.к. балка под действием нагрузки изгибается и полного защемления нет.
На практике отдельно колонну не считают, а моделируют в программе раму или 3-х мерную модель здания, нагружают ее и рассчитывают колонну в сборке и подбирают необходимый профиль, но в программах бывает трудно учесть ослабление сечения отверстиями от болтов, поэтому бывает необходимо проверять сечение вручную.
Чтобы рассчитать колонну нам необходимо знать максимальные сжимающие/растягивающие напряжения и моменты, возникающие в ключевых сечениях, для этого строят эпюры напряжения. В данном обзоре мы рассмотрим только прочностной расчет колонны без построения эпюр.
Расчет колонны производим по следующим параметрам:
1. Прочность при центральном растяжении/сжатии
2. Устойчивость при центральном сжатии (в 2-х плоскостях)
3. Прочность при совместном действии продольной силы и изгибающих моментов
4. Проверка предельной гибкости стержня (в 2-х плоскостях)
1. Прочность при центральном растяжении/сжатии
Согласно СП 16.13330 п. 7.1.1 расчет на прочность элементов из стали с нормативным сопротивлением Ryn ≤ 440 Н/мм2 при центральном растяжении или сжатии силой N следует выполнять по формуле
где N — нагрузка на сжатие/растяжение;
An — площадь поперечного сечения профиля нетто, т.е. с учетом ослабления его отверстиями;
Ry — расчетное сопротивление стали проката (зависит от марки стали см. Таблицу В.5 СП 16.13330);
γс — коэффициент условий работы (см. Таблицу 1 СП 16.13330).
По этой формуле можно вычислить минимально-необходимую площадь сечения профиля и задать профиль. В дальнейшем в проверочных расчетах подбор сечения колонны можно будет сделать только методом подбора сечения, поэтому здесь мы можем задать отправную точку, меньше которой сечение быть не может.
2. Устойчивость при центральном сжатии
Расчет на устойчивость производится согласно СП 16.13330 п. 7.1.3 по формуле
где N — нагрузка на сжатие/растяжение;
A — площадь поперечного сечения профиля брутто, т.е.без учета ослабления его отверстиями;
Ry — расчетное сопротивление стали;
γс — коэффициент условий работы (см. Таблицу 1 СП 16.13330);
φ — коэффициент устойчивости при центральном сжатии.
Как видим эта формула очень напоминает предыдущую, но здесь появляется коэффициент φ, чтобы его вычислить нам вначале потребуется вычислить условную гибкость стержня λ (обозначается с чертой сверху).
где Ry — расчетно сопротивление стали;
E — модуль упругости;
λ — гибкость стержня, вычисляемая по формуле:
где lef — расчетная длина стержня;
i — радиус инерции сечения.
Расчетные длины lef колонн (стоек) постоянного сечения или отдельных участков ступенчатых колонн согласно СП 16.13330 п. 10.3.1 следует определять по формуле
где l — длина колонны;
μ — коэффициент расчетной длины.
Коэффициенты расчетной длины μ колонн (стоек) постоянного сечения следует определять в зависимости от условий закрепления их концов и вида нагрузки. Для некоторых случаев закрепления концов и вида нагрузки значения μ приведены в следующей таблице:
Радиус инерции сечения можно найти в соответствующем ГОСТ-е на профиль, т.е. предварительно профиль должен быть уже задан и расчет сводится к перебору сечений.
Т.к. радиус инерции в 2-х плоскостях для большинства профилей имеет разные значения на 2-х плоскостей (одинаковые значения имеют только труба и квадратный профиль) и закрепление может быть разным, а следственно и расчетные длины тоже могут быть разные, то расчет на устойчивость необходимо произвести для 2-х плоскостей.
Итак теперь у нас есть все данные чтобы рассчитать условную гибкость.
Если предельная гибкость больше или равна 0,4, то коэффициент устойчивости φ вычисляется по формуле:
значение коэффициента δ следует вычислить по формуле:
коэффициенты α и β смотрите в таблице

Значения коэффициента φ, вычисленные по этой формуле, следует принимать не более (7,6/ λ 2) при значениях условной гибкости свыше 3,8; 4,4 и 5,8 для типов сечений соответственно а, b и с.
При значениях λ < 0,4 для всех типов сечений допускается принимать φ = 1.
Значения коэффициента φ приведены в приложении Д СП 16.13330.
Теперь когда все исходные данные известны производим расчет по формуле, представленной вначале:
Как уже было сказано выше, необходимо сделать 2-а расчета для 2-х плоскостей. Если расчет не удовлетворяет условию, то подбираем новый профиль с более большим значением радиуса инерции сечения. Также можно изменить расчетную схему, например изменив шарнирную заделку на жесткую или закрепив связями колонну в пролете можно уменьшить расчетную длину стержня.
Сжатые элементы со сплошными стенками открытого П-образного сечения рекомендуется укреплять планками или решеткой. Если планки отсутствуют, то устойчивость следует проверять на устойчивость при изгибно-крутильной форме потери устойчивости согласно п.7.1.5 СП 16.13330.
3. Прочность при совместном действии продольной силы и изгибающих моментов
Как правило колонна нагружена не только осевой сжимающей нагрузкой, но и изгибающем моментом, например от ветра. Момент также образуется если вертикальная нагрузка приложена не по центру колонны, а сбоку. В этом случае необходимо сделать проверочный расчет согласно п. 9.1.1 СП 16.13330 по формуле
где N — продольная сжимающая сила;
An — площадь сечения нетто (с учетом ослабления отверстиями);
Ry — расчетное сопротивление стали;
γс — коэффициент условий работы (см. Таблицу 1 СП 16.13330);
n, Сx и Сy — коэффициенты принимаемые по таблице Е.1 СП 16.13330


Mx и My — моменты относительно осей X-X и Y-Y;
Wxn,min и Wyn,min — моменты сопротивления сечения относительно осей X-X и Y-Y (можно найти в ГОСТ-е на профиль или в справочнике);
B — бимомент, в СНиП II-23-81* этого параметра не было в расчетах, этот параметр ввели для учета депланации;
Wω,min – секторальный момент сопротивления сечения.
Если с первыми 3-мя составляющими вопросов быть не должно, то учет бимомента вызывает некоторые трудности.
Бимомент характеризует изменения, вносимые в линейные зоны распределения напряжений депланации сечения и, по сути, является парой моментов, направленных в противоположные стороны

Стоит отметить, что многие программы не могут рассчитать бимомент, в том числе и SCAD его не учитывает.
4. Проверка предельной гибкости стержня
Гибкости сжатых элементов λ= lef / i, как правило, не должны превышать предельных значений λu, приведенных в таблице

Коэффициент α в данной формуле это коэффициент использования профиля, согласно расчету на устойчивость при центральном сжатии.
Также как и расчет на устойчивость данный расчет нужно сделать для 2-х плоскостей.
В случае если профиль не подходит необходимо изменить сечение увеличив радиус инерции сечения или изменив расчетную схему (изменить закрепления или закрепить связями чтобы уменьшить расчетную длину).
Если критическим фактором является предельная гибкость, то марку стали можно взять наименьшую т.к. на предельную гибкость марка стали не влияет. Оптимальный вариант можно вычислить методом подбора.
Источник
На чтение 4 мин. Просмотров 3.5k. Обновлено 25 ноября, 2020
Расположенный ниже онлайн калькулятор предназначен для расчёта центрально-нагруженной стойки (колонны) из стального проката круглого, квадратного, прямоугольного и шестигранного сечения на прочность, устойчивость и изгиб. Если Вам нужно рассчитать онлайн прочность, изгиб и устойчивость стойки из СТАЛЬНЫХ ТРУБ, смотрите ТУТ . Или расчет стойки из ШВЕЛЛЕРА, ДВУТАВРА, ТАВРА и УГОЛКА на прочность, устойчивость и гибкость.
При проектировании строительных конструкций, необходимо принимать схемы, обеспечивающие прочность, устойчивость и пространственную неизменяемость сооружения в целом, а также его отдельных элементов при монтаже и эксплуатации.
Поэтому стойку, находящуюся под действием сжимающей её нагрузки необходимо проверять:
- На прочность;
- Устойчивость;
- Допустимую гибкость.
Для расчета предлагаем вам воспользоваться онлайн калькулятором, специально разработанным для нашего сайта!
Онлайн калькулятор для расчёта стойки (колонны) из стального проката
| Материал проката | Вид и назначение стоек (колонн) |
Если Вашего материала нет в таблице, но Вам известно рассчётное
сопротивление этого материала, ведите его значение в это поле (кг/см2):
Введите параметры для расчёта
| Длина стойки L, м | Размер D или Dv, или A, им |
| Размер B, мм | Нагрузка на стойку P, кг |
Логика онлайн расчета на прочность и устойчивость стойки из стального проката
Согласно Актуализированной редакция СНиП II-23-81 (CП16.13330, 2011) рассчитывая на прочность элементов из стали при центральном растяжении или сжатии силой P следует выполнять по формуле:
P / Fp * Ry * Yc <= 1
- где P – действующая нагрузка.
- Fp – площадь поперечного сечения колонны.
- Ry – подсчетное сопротивление материала (стали колонны), выбирается по таблице В5 Приложения “В” того же СНиПа.
- Yc – коэффициент условий работы по таблице 1 СНиПа (0.9-1.1). В соответствии с примечанием к этой таблице (пункт 5) в калькуляторе принято Yc=1.
Проверку на устойчивость элементов сплошного сечения при центральном сжатии силой P следует выполнять по формуле:
P / Fi * Fp * Ry * Yc <= 1
где Fi – коэффициент продольного изгиба центрально – сжатых элементов.
Коэффициент Fi введён в качестве компенсации возможности некоторой не прямолинейности колонны, недостаточной жесткости её крепления и неточности в приложении нагрузки относительно оси стойки.
Значение Fi зависит от марки стали и гибкости колонны и часто берётся из таблицы 72 СНиП II-23-81 1990г., исходя из гибкости колонны и расчётного сопротивления выбранной стали сжатию, растяжению и изгибу.
Это несколько упрощает и огрубляет вычисления, так как СНиП II-23-81* предусматривает специальные формулы для определения Fi. Гибкость (Lambda) – некоторая величина, характеризующая свойства рассматриваемого стержня в зависимости от его длины и параметров поперечн. сечения, в частности радиуса инерции:
Lambda = Lr / i
- здесь Lr – расчётная длина стержня,
- i – радиус инерции поперечного сечения стержня (колонны).
Радиус инерции сечения i равен корню квадратному из выражения I / Fp, где I – момент инерции, Fp – его площадь.
Lr (расчётная длина) определяется как Mu*L; здесь L – длина стойки, а Mu – коэфф., зависящий от схемы её крепления:
- “заделка-консоль”(свободный конец) – Mu=2;
- “заделка-заделка” – Mu = 0.5;
- заделка – шарнир” – Mu = 0.7;
- “шарнир – шарнир” – Mu = 1.
Следует иметь ввиду,что при наличии у формы поперечн. сечения 2-ух радиусов инерции (например, у прямоугольника), при вычислении Lambda используется меньший.
Кроме того, сама Lambda (гибкость колонны), рассчитанная по формуле Lambda = Lr / i не должна превышать 220-ти в соответствии с таблицей 19. СНиП II-23-81*; там же содержатся ограничения на предельную гибкость центрально – сжатых стержней.
Для их использования необходимо сделать выбор в таблице онлайн калькулятора “Вид, назначение стоек”. Предельная гибкость стоек, кроме их геометрических параметров, зависит также от коэффициента продольного изгиба (Fi), действующей нагрузки (P), расчётного сопротивления материала стоики (Ry) и условий её работы (Yc).
Предельная гибкость, устойчивость и прочность стоек, кроме их геометрических параметров, зависит также от коэффициента продольного изгиба (Fi), действующей нагрузки (P), расчётного сопротивления материала стойки (Ry) и условий её работы (Yc).
Если возникнут трудности при расчетах онлайн калькулятором прочности и устойчивости, рекомендуем предварительно ознакомиться с инструкцией.
Источник
Часто люди, делающие во дворе крытый навес для автомобиля или для защиты от солнца и атмосферных осадков, сечение стоек, на которые будет опираться навес, не рассчитывают, а подбирают сечение на глаз или проконсультировавшись у соседа.
Понять их можно, нагрузки на стойки, в данном случае являющиеся колоннами, не ахти какие большие, объем выполняемых работ тоже не громадный, да и внешний вид колонн иногда намного важнее их несущей способности, поэтому даже если колонны будут сделаны с многократным запасом по прочности — большой беды в этом нет. Тем более, что на поиски простой и внятной информации о расчете сплошных колонн можно потратить бесконечное количество времени без какого-либо результата — разобраться в примерах расчета колонн для производственных зданий с приложением нагрузки в нескольких уровнях без хороших знаний сопромата практически невозможно, а заказ расчета колонны в инженерной организации может свести всю ожидаемую экономию к нулю.
Данная статья написана с целью хоть немного изменить существующее положение дел и является попыткой максимально просто изложить основные этапы расчета металлической колонны, не более того. Все основные требования по расчету металлических колонн можно найти в СНиП II-23-81 (1990).
Общие положения
С теоретической точки зрения расчет центрально-сжатого элемента, каковым является колонна, или стойка в ферме, настолько прост, что даже неудобно об этом говорить. Достаточно разделить нагрузку на расчетное сопротивление стали, из которой будет изготавливаться колонна — все. В математическом выражении это выглядит так:
F = N/Ry (1.1)
где
F — требуемая площадь сечения колонны, см²
N — сосредоточенная нагрузка, прилагаемая к центру тяжести поперечного сечения колонны, кг;
Ry — расчетное сопротивление металла растяжению, сжатию и изгибу по пределу текучести, кг/см². Значение расчетного сопротивления можно определить по соответствующей таблице.
Как видим, уровень сложности задачи относится ко второму, максимум к третьему классу начальной школы. Однако на практике все далеко не так просто, как в теории, по ряду причин:
1. Приложить сосредоточенную нагрузку точно к центру тяжести поперечного сечения колонны можно только теоретически. В реальности нагрузка всегда будет распределенной и еще будет некоторый эксцентриситет приложения приведенной сосредоточенной нагрузки. А раз есть эксцентриситет, значит есть продольный изгибающий момент действующий в поперечном сечении колонны.
2. Центры тяжести поперечных сечений колонны расположены на одной прямой — центральной оси, тоже только теоретически. На практике из-за неоднородности металла и различных дефектов центры тяжести поперечных сечений могут быть смещены относительно центральной оси. А это значит, что расчет нужно производить по сечению, центр тяжести которого максимально удален от центральной оси, из-за чего эксцентриситет действия силы для этого сечения максимальный.
3. Колонна может иметь не прямолинейную форму, а быть немного изогнутой в результате заводской или монтажной деформации а это значит, что поперечные сечения в средней части колонны будут иметь наибольший эксцентриситет приложения нагрузки.
4. Колонна может быть установлена с отклонениями от вертикали, а это значит, что вертикально действующая нагрузка может создавать дополнительный изгибающий момент, максимальный в нижней части колонны, а если точнее, в месте крепления к фундаменту, впрочем это актуально, только для отдельно стоящих колонн.
5. Под действием приложенных к ней нагрузок колонна может деформироваться, а это значит, что опять появится эксцентриситет приложения нагрузки и как следствие дополнительный изгибающий момент.
6. В зависимости от того, как именно закреплена колонна, зависит значение дополнительного изгибающего момента внизу и в средней части колонны.
Все это приводит к появлению продольного изгиба и влияние это изгиба при расчетах нужно как-то учитывать.
Естественно, что рассчитать вышеуказанные отклонения для конструкции, которая еще только проектируется, практически невозможно — расчет будет очень долгим, сложным, а результат все равно сомнительным. А вот ввести в формулу (1.1) некий коэффициент, который бы учел вышеизложенные факторы, очень даже можно. Таким коэффициентом является φ — коэффициент продольного изгиба. Формула, в которой используется данный коэффициент, выглядит так:
F = N/φR (1.2)
Значение φ всегда меньше единицы, это означает, что сечение колонны всегда будет больше, чем если просто посчитать по формуле (1.1), это я к тому, что сейчас начнется самое интересное и помнить, что φ всегда меньше единицы — не помешает. Для предварительных расчетов можно использовать значение φ в пределах 0,5-0,8. Значение φ зависит от марки стали и гибкости колонны λ:
λ = lef/i (1.3)
где
lef — расчетная длина колонны. Расчетная и реальная длина колонны — разные понятия. Расчетная длина колонны зависит от способа закрепления концов колонны и определяется с помощью коэффициента μ:
lef = μl (1.4)
где
l — реальная длина колонны, см;
μ — коэффициент, учитывающий способ закрепления концов колонны. Значение коэффициента можно определить по следующей таблице:
Таблица 1. Коэффициенты μ для определения расчетных длин колонн и стоек постоянного сечения (согласно СНиП II-23-81 (1990))
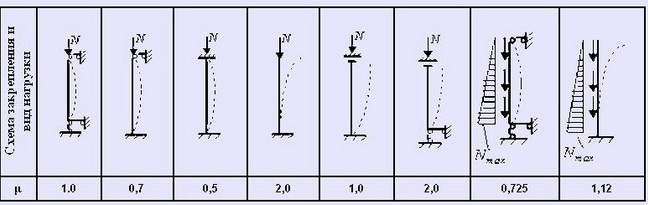
Как видим, значение коэффициента μ изменяется в несколько раз в зависимости от способа закрепления колонны и тут главная сложность в том, какую расчетную схему выбрать. Если не знаете, какая схема закрепления соответствует Вашим условиям, то принимайте значение коэффициента μ=2. Значение коэффициента μ=2 принимается в основном для отдельно стоящих колон, наглядный пример отдельно стоящей колонны — фонарный столб. Значение коэффициента μ=1-2 можно принимать для колонн навесов, на которые опираются балки без жесткого крепления к колонне. Данную расчетную схему можно принимать, когда балки навеса будут не жестко крепиться к колоннам и когда балки будут иметь относительно большой прогиб. Если на колонну будут опираться фермы, жестко прикрепленные к колонне сваркой, то можно принимать значение коэффициента μ=0,5-1. Если между колоннами будут диагональные связи, то можно принимать значение коэффициента μ=0,7 при нежестком креплении диагональных связей или 0,5 при жестком креплении. Однако такие диафрагмы жесткости не всегда бывают в 2 плоскостях и потому использовать такие значения коэффициента нужно осторожно. При расчете стоек ферм используется коэффициент μ=0,5-1 в зависимости от метода закрепления стоек.
Значение коэффициента гибкости приблизительно показывает отношение расчетной длины колонны к высоте или ширине поперечного сечения. Т.е. чем больше значение λ, тем меньше ширина или высота поперечного сечения колонны и соответственно тем больший запас по сечению потребуется при одной и той же длине колонны, но об этом чуть позже.
Теперь когда мы определили коэффициент μ, можно вычислить расчетную длину колонны по формуле (1.4), а для того, чтобы узнать значение гибкости колонны, нужно знать радиус инерции сечения колонны i:
(1.5)
где I — момент инерции поперечного сечения относительно одной из осей, и тут начинается самое интересное, потому как в ходе решения задачи мы как раз и должны определить необходимую площадь сечения колонны F, но этого мало, оказывается, мы еще должны знать значение момента инерции. Так как мы не знаем ни того, ни другого, то решение задачи выполняется в несколько этапов.
На предварительном этапе обычно принимается значение λ в пределах 90-60, для колонн с относительно небольшой нагрузкой можно принимать λ = 150-120 (максимальное значение для колонн — 180, значения предельной гибкости для других элементов можно узнать по таблице 19* СНиП II-23-81 (1990). Затем по Таблице 2 определяется значение коэффициента гибкости φ:
Таблица 2. Коэффициенты продольного изгиба φ центрально-сжатых элементов.
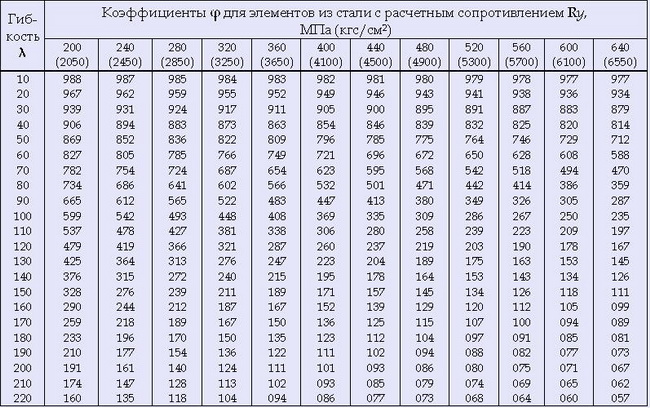
Примечание: значения коэффициента φ в таблице увеличены в 1000 раз.
После этого определяется требуемый радиус инерции поперечного сечения, путем преобразования формулы (1.3):
i = lef/λ (1.6)
По сортаменту подбирается прокатный профиль с соответствующим значением радиуса инерции. В отличие от изгибаемых элементов, где сечение подбирается только по одной оси, так как нагрузка действует только в одной плоскости, в центрально сжатых колоннах продольный изгиб может произойти относительно любой из осей и потому чем ближе значение Iz к Iy, тем лучше, другими словами наиболее предпочтительны профили круглого или квадратного сечения. Ну а теперь попробуем определить сечение колонны на основе полученных знаний.
Пример расчета металлической центрально-сжатой колонны
Имеется: желание сделать навес возле дома приблизительно следующего вида:
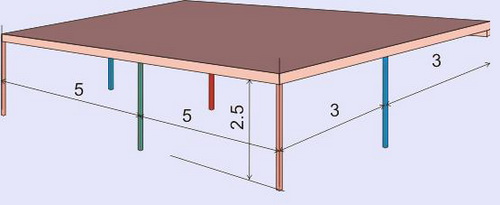
В данном случае единственной центрально-сжатой колонной при любых условиях закрепления и при равномерно распределенной нагрузке будет колонна, показанная на рисунке красным цветом. Кроме того и нагрузка на эту колонну будет максимальной. Колонны, обозначенные на рисунке синим и зеленым цветом, можно рассматривать как центрально-сжатые, только при соответствующем конструктивном решении и равномерно-распределенной нагрузке, колонны, обозначенные оранжевым цветом, будут или центрально сжатыми или внецентренно-сжатыми или стойками рамы, рассчитываемой отдельно. В данном примере мы рассчитаем сечение колонны, обозначенной красным цветом. Для расчетов примем постоянную нагрузку от собственного веса навеса 100 кг/м² и временную нагрузку 100 кг/м² от снегового покрова.
2.1. Таким образом сосредоточенная нагрузка на колонну, обозначенную красным цветом, составит:
N = (100+100)·5·3 = 3000 кг
2.2. Принимаем предварительно значение λ = 100, тогда по таблице 2 коэффициент изгиба φ = 0,599 (для стали с расчетной прочностью 200 МПа, данное значение принято для обеспечения дополнительного запаса по прочности), тогда требуемая площадь сечения колонны:
F = 3000/(0,599·2050) = 2,44 см²
2.3. По таблице 1 принимаем значение μ = 1 (так как кровельное покрытие из профилированного настила, должным образом закрепленное, будет обеспечивать жесткость конструкции в плоскости, параллельной плоскости стены, а в перпендикулярной плоскости относительную неподвижность верхней точки колонны будет обеспечивать крепление стропил к стене), тогда радиус инерции
i = 1·250/100 = 2,5 cм
2.4. По сортаменту для квадратных профильных труб данным требованиям удовлетворяет профиль с размерами поперечного сечения 70х70 мм с толщиной стенки 2 мм, имеющий радиус инерции 2,76 см. Площадь сечения такого профиля 5,34 см². Это намного больше, чем требуется по расчету.
2.5.1. Мы можем увеличить гибкость колонны, при этом требуемый радиус инерции уменьшится. Например, при λ = 130 коэффициент изгиба φ = 0,425, тогда требуемая площадь сечения колонны:
F = 3000/(0,425·2050) = 3,44 см²
2.5.2. Тогда
i = 1·250/130 = 1,92 cм
2.5.3. По сортаменту для квадратных профильных труб данным требованиям удовлетворяет профиль с размерами поперечного сечения 50х50 мм с толщиной стенки 2 мм, имеющий радиус инерции 1,95 см. Площадь сечения такого профиля 3,74 см², момент сопротивления для этого профиля составляет 5,66 см³.
Вместо квадратных профильных труб можно использовать равнополочный уголок, швеллер, двутавр, обычную трубу. Если расчетное сопротивление стали выбранного профиля больше 220 МПа, то можно пересчитать сечение колонны. Вот в принципе и все, что касается расчета металлических центрально-сжатых колонн.
Расчет внецентренно-сжатой колонны
Тут конечно же возникает вопрос: а как рассчитать остальные колонны? Ответ на этот вопрос сильно зависит от способа крепления навеса к колоннам. Если балки навеса будут жестко крепиться к колоннам, то при этом будет образована достаточно сложная статически неопределимая рама и тогда колонны следует рассматривать как часть этой рамы и рассчитывать сечение колонн дополнительно на действие поперечного изгибающего момента, мы же далее рассмотрим ситуацию когда колонны, показанные на рисунке, соединены с навесом шарнирно (колонну, обозначенную красным цветом, мы больше не рассматриваем). Например оголовок колонн имеет опорную площадку — металлическую пластину с отверстиями для болтового крепления балок навеса. По разным причинам нагрузка на такие колонны может передаваться с достаточно большим эксцентриситетом:
Балка, показанная на рисунке, бежевым цветом, под воздействием нагрузки немного прогнется и это приведет к тому, что нагрузка на колонну будет передаваться не по центру тяжести сечения колонны, а с эксцентриситетом е и при расчете крайних колонн этот эксцентриситет нужно учитывать. Случаев внецентренного нагружения колонн и возможных поперечных сечений колонн существует великое множество, описываемое соответствующими формулами для расчета. В нашем случае для проверки сечения внецентренно-сжатой колонны мы воспользуемся одной из самых простых:
(N/φF) + (Mz/Wz) ≤ Ry (3.1)
В данном случае, когда сечение самой нагруженной колонны мы уже определили, нам достаточно проверить, подходит ли такое сечение для остальных колонн по той причине, что задачи строить сталелитейный завод у нас нет, а мы просто рассчитываем колонны для навеса, которые будут все одинакового сечения из соображений унификации.
Что такое N, φ и Ry мы уже знаем.
Формула (3.1) после простейших преобразований, примет следующий вид:
F = (N/Ry)(1/φ + ez·F/Wz) (3.2)
так как Мz=N·ez, почему значение момента именно такое и что такое момент сопротивления W, достаточно подробно объясняется в отдельной статье.
Сосредоточенная нагрузка N на колонны, обозначенные на рисунке синим и зеленым цветом, составит 1500 кг. Проверяем требуемое сечение при такой нагрузке и ранее определенном φ = 0,425
F = (1500/2050)(1/0,425 + 2,5·3,74/5,66) = 0,7317·(2,353 + 1,652) = 2,93 см²
Кроме того, формула (3.2) позволяет определить максимальный эксцентриситет, который выдержит уже рассчитанная колонна, в данном случае максимальный эксцентриситет составит 4,17 см.
Требуемое сечение 2,93 см² меньше принятого 3,74 см², а потому квадратную профильную трубу с размерами поперечного сечения 50х50 мм с толщиной стенки 2 мм можно использовать и для крайних колонн.
Расчет внецентренно-сжатой колонны по условной гибкости
Как ни странно, но для подбора сечения внецентренно-сжатой колонны — сплошного стержня есть еще более простая формула:
F = N/φеR (4.1)
где
φе — коэффициент продольного изгиба, зависящий от эксцентриситета, его можно было бы назвать эксцентриситетным коэффициентом продольного прогиба, чтобы не путать с коэффициентом продольного прогиба φ. Однако расчет по этой формуле может оказаться более длительным чем по формуле (3.2). Чтобы определить коэффициент φе необходимо все равно знать значение выражения ez·F/Wz — которое мы встречали в формуле (3.2). Это выражение называется относительным эксцентриситетом и обозначается m:
m = ez·F/Wz (4.2)
После этого определяется приведенный относительный эксцентриситет:
mef = hm (4.3)
где
h — это не высота сечения, а коэффициент, определяемый по таблице 73 СНиПа II-23-81. Просто скажу, что значение коэффициента h изменяется в пределах от 1 до 1,4, для большинства простых расчетов можно использовать h = 1,1-1,2.
После этого нужно определить условную гибкость колонны λ¯:
λ¯ = λ√‾(Ry / E) (4.4)
и только после этого по таблице 3 определить значение φе:
Таблица 3. Коэффициенты φe для проверки устойчивости внецентренно-сжатых (сжато-изгибаемых) сплошностенчатых стержней в плоскости действия момента, совпадающей с плоскостью симметрии.
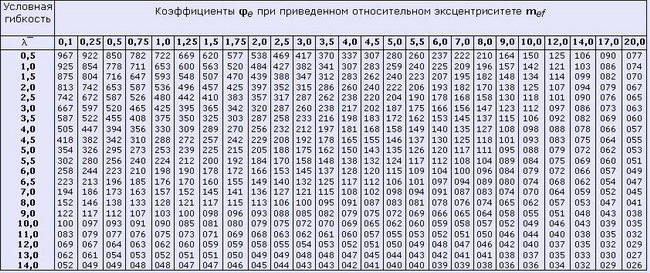
Примечания:
1. Значения коэффициента φе увеличены в 1000 раз.
2. Значение φе следует принимать не более φ.
Теперь для наглядности проверим сечение колонн, нагруженных с эксцентриситетом, по формуле (4.1):
4.1. Сосредоточенная нагрузка на колонны, обозначенные синим и зеленым цветом, составит:
N = (100+100)·5·3/2 = 1500 кг
Эксцентриситет приложения нагрузки е = 2,5 см, коэффициент продольного изгиба φ =
