Расчет конструкций на растяжение сжатие сдвиг

Внутренние усилия при растяжении-сжатии.
Осевое (центральное) растяжение или сжатие прямого бруса вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса. При растяжении или сжатии в поперечных сечениях бруса возникают только продольные силы N. Продольная сила N в некотором сечении равна алгебраической сумме проекции на ось стержня всех внешних сил, действующих по одну сторону от рассматриваемого сечения. По правилу знаков продольной силы N принято считать, что от растягивающих внешних нагрузок возникают положительные продольные силы N, а от сжимающих — продольные силы N отрицательны (рис. 5).

Чтобы выявить участки стержня или его сечения, где продольная сила имеет наибольшее значение, строят эпюру продольных сил, применяя метод сечений, подробно рассмотренный в статье:
Анализ внутренних силовых факторов в статистически определимых системах
Ещё настоятельно рекомендую взглянуть на статью:
Расчёт статистически определимого бруса
Если разберёте теорию в данной статье и задачи по ссылкам, то станете гуру в теме «Растяжение-сжатие» =)
Напряжения при растяжении-сжатии.
Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:

где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.
Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:

Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.
Деформации при растяжении-сжатии.
Рассмотрим деформации, возникающие при растяжении (сжатии) стержня (рис.6, а). Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l1 и его длины до деформации l

Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением, или относительной продольной деформацией:

При растяжении продольная деформация положительна, а при сжатии – отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:

где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).
Таблица 1
Модуль продольной упругости для различных материалов

Абсолютная поперечная деформация бруса равна разности размеров поперечного сечения после и до деформации:

Соответственно, относительную поперечную деформацию определяют по формуле:

При растяжении размеры поперечного сечения бруса уменьшаются, и ε’ имеет отрицательное значение. Опытом установлено, что в пределах действия закона Гука при растяжении бруса поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε’ к продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона μ:

Экспериментально установлено, что на упругой стадии нагружения любого материала значение μ = const и для различных материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5 (табл. 2).
Таблица 2
Коэффициент Пуассона.

Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N:

Данной формулой можно пользоваться для вычисления абсолютного удлинения участка стержня длиной l при условии, что в пределах этого участка значение продольной силы постоянно. В случае, когда продольная сила N изменяется в пределах участка стержня, Δl определяют интегрированием в пределах этого участка:

Произведение (Е·А) называют жесткостью сечения стержня при растяжении (сжатии).
Механические свойства материалов.
Основными механическими свойствами материалов при их деформации являются прочность, пластичность, хрупкость, упругость и твердость.
Прочность — способность материала сопротивляться воздействию внешних сил, не разрушаясь и без появления остаточных деформаций.
Пластичность – свойство материала выдерживать без разрушения большие остаточные деформации. Неисчезающие после снятия внешних нагрузок деформации называются пластическими.
Хрупкость – свойство материала разрушаться при очень малых остаточных деформациях (например, чугун, бетон, стекло).
Идеальная упругость – свойство материала (тела) полностью восстанавливать свою форму и размеры после устранения причин, вызвавших деформацию.
Твердость – свойство материала сопротивляться проникновению в него других тел.
Рассмотрим диаграмму растяжения стержня из малоуглеродистой стали. Пусть круглый стержень длинной l0 и начальным постоянным поперечным сечением площади A0 статически растягивается с обоих торцов силой F.

Диаграмма сжатия стержня имеет вид (рис. 10, а)

где Δl = l — l0 абсолютное удлинение стержня; ε = Δl / l0 — относительное продольное удлинение стержня; σ = F / A0 — нормальное напряжение; E — модуль Юнга; σп — предел пропорциональности; σуп — предел упругости; σт — предел текучести; σв — предел прочности (временное сопротивление); εост — остаточная деформация после снятия внешних нагрузок. Для материалов, не имеющих ярко выраженную площадку текучести, вводят условный предел текучести σ0,2 — напряжение, при котором достигается 0,2% остаточной деформации. При достижении предела прочности в центре стержня возникает локальное утончение его диаметра («шейка»). Дальнейшее абсолютное удлинение стержня идет в зоне шейки ( зона местной текучести). При достижении напряжением предела текучести σт глянцевая поверхность стержня становится немного матовой – на его поверхности появляются микротрещины (линии Людерса-Чернова), направленные под углом 45° к оси стержня.

Расчеты на прочность и жесткость при растяжении и сжатии.
Опасным сечением при растяжении и сжатии называется поперечное сечение бруса, в котором возникает максимальное нормальное напряжение. Допускаемые напряжения вычисляются по формуле:

где σпред — предельное напряжение (σпред = σт — для пластических материалов и σпред = σв — для хрупких материалов); [n] — коэффициент запаса прочности. Для пластических материалов [n] = [nт] = 1,2 … 2,5; для хрупких материалов [n] = [nв] = 2 … 5, а для древесины [n] = 8 ÷ 12.
Расчеты на прочность при растяжении и сжатии.
Целью расчета любой конструкции является использование полученных результатов для оценки пригодности этой конструкции к эксплуатации при минимальном расходе материала, что находит отражение в методах расчета на прочность и жесткость.
Условие прочности стержня при его растяжении (сжатии):

При проектном расчете определяется площадь опасного сечения стержня:

При определении допускаемой нагрузки рассчитывается допускаемая нормальная сила:

Расчет на жесткость при растяжении и сжатии.
Работоспособность стержня определяется его предельной деформацией [ l ]. Абсолютное удлинение стержня должно удовлетворять условию:

Часто дополнительно делают расчет на жесткость отдельных участков стержня.
Следующая важная статья теории:
Изгиб балки
Источник
2.4.1 Растяжение (сжатие).
Растяжением (сжатием) называется такой вид деформации, при котором в поперечном (перпендикулярном оси) сечении стержня возникает только продольная растягивающая (сжимающая) сила. Модель растягиваемого стержня широко используется в расчетах болтов, ремней передач, стержней ферм, лопаток турбин и др. Для определения величины продольной силы Fz используют метод сечений (Рисунок 48).
Продольная сила Fz, приложенная в центре тяжести произвольного сечения стержня, является равнодействующей внутренних сил dFz =σdA, действующих на бесконечно малые площадки поперечного сечения площадью А:
Из этого уравнения нельзя найти закон распределения нормальных напряжений по поперечному сечению. Однако, если предположить, что в пределах действия закона Гука плоские поперечные сечения стержня смещаются при растяжении параллельно начальным положениям, оставаясь плоскими, то нормальные напряжения во всех точках сечения должны быть одинаковыми, т.е. σ= соnst, тогда Fz = σA и σ = Fz/A.
Таким образом, нормальное напряжение в поперечном сечении стержня при растяжении равно отношению продольной силы к площади сечения.
При сжатии стержня напряжения имеют отрицательный знак: нормальная сила направлена в тело стержня. Нормальные напряжения в элементах конструкций не должны превышать допускаемые напряжения:
Данное условие прочности при растяжении позволяет решать задачи расчета элементов конструкций на прочность:
1) При известных размерах поперечного сечения детали А и известном допускаемом напряжении [σ] определяют допускаемые нагрузки: .
Рис 48.
2) Определяют площадь поперечного сечения по заданной силе и допускаемому напряжению.
, для круга: ;
3) При известной силе и площади поперечною сечения детали определяют напряжения и проверяют, не превышают ли они допускаемые:
.
Итак, напряжения при растяжении (сжатии) . С другой стороны, согласно закона Гука в пределах малых деформаций напряжения прямо пропорциональны вызываемой ими относительной деформации. Так как относительная деформация , тогда , откуда . То есть, в пределах малых деформаций абсолютное продольное удлинение прямо пропорционально силе Fz и первоначальной длине стержня lo и обратно пропорционально модулю упругости E и площади поперечного сечения А. Произведение ЕА называется жесткостью сечения стержня при растяжении (сжатии).
В некоторых случаях при работе конструкции на сжатие работоспособность ее определяю! не величиной допускаемой нагрузки или допускаемого напряжения, а величиной допускаемой деформации. В том случае находят фактическое абсолютное удлинение и сопоставляют его с допускаемым, такие расчеты называются расчетами на жесткость:
— сосредоточенная нагрузка или
— распределенная нагрузка.
Опыты показывают, что удлинение стержня в осевом направлении при растяжении сопровождается уменьшением его поперечных размеров, т.е. наряду с продольной возникает поперечная деформация стержня.
2.4.2 Смятие.
Если два тела подвергаются сжимающей нагрузке и соприкасаются между собой, то общие поверхности соприкосновения называют поверхностями контакта. На поверхностях контакта возникают напряжения смятия. При расчете на смятие допускают, что силы взаимодействия равномерно распределены по поверхности соприкосновения и в каждой точке нормальны к пой поверхности, т.е. возникают нормальные напряжения. Элементарная сила на элементарной площадке . Полная сила .
Тогда, основное условие прочности на смятие . Допускаемое напряжение на смятие (Рисунок 49. а).
Если контакт деталей осуществляется по поверхности полуцилиндра, то площадь смятия определяется как проекция поверхности контакта на диаметральную плоскость (Рисунок 49. б).
Рис 49.
Для многих деталей контакт происходит не по площади, а по линии или точке. В этом случае напряжения смятия определяют по теории контактных напряжений.
Под действием нагрузки, прижимающей тела друг к другу в направлении по нормали к их поверхностям, в поверхностных слоях материала деталей возникают местные деформации и контактные напряжения. Давления по площадке контакта распределяются по эллиптическому закону. Максимальные контактные напряжения возникают в центре (точке контакта) (Рисунок 50. а). Контактные напряжения определяются по формуле Беляева-Герца
μ — коэффициент Пуассона;
— интенсивность силы давления по длине контактной линии;
— приведенный модуль упругости материалов, при ; ;
Рис 50.
— приведенная кривизна поверхностей в месте контакта (Рисунок 50. а).
Знак «-» — одна из поверхностей вогнута. Если одна поверхность прямолинейна (т.е. р2 = ∞), то ρпр = ρ1, (Рисунок 50. б, в).
2.4.3 Сдвиг.
Сдвиг — это деформация, вызываемая противоположно направленными силами, лежащими в близких параллельных плоскостях. Результатом сдвига является срез, например, резание материала ручными или механическими ножницами (Рисунок 51).
При сдвиге происходит перекашивание прямых углов элементарных параллелепипедов. Степень деформирования определяется величиной, которая называется абсолютной деформацией (абсолютным сдвигом). Деформация сдвига, доведенная до разрушения, называется срезом. Отношение абсолютного сдвига к расстоянию между сдвигающимися сечениями — относительная деформация (относительный сдвиг) .
В виду малости величин (Рисунок 51. б). Величина у — относительный сдвиг или угол сдвига.
Внутренние силы, уравновешивающие внешние силы, приложенные к отмеченной части, называются поперечными (перерезывающими силами) FQy, т.к. они действуют перпендикулярно оси стержня.
Поперечная сила складывается как сумма элементарных внутренних сил
(Рисунок 51. в).
Если принять допущение, что касательные напряжения распределяются по сечению равномерно и равны, т.е. .
Источник

Расчет панелей в конструкции самолета Растяжение Сжатие Сдвиг

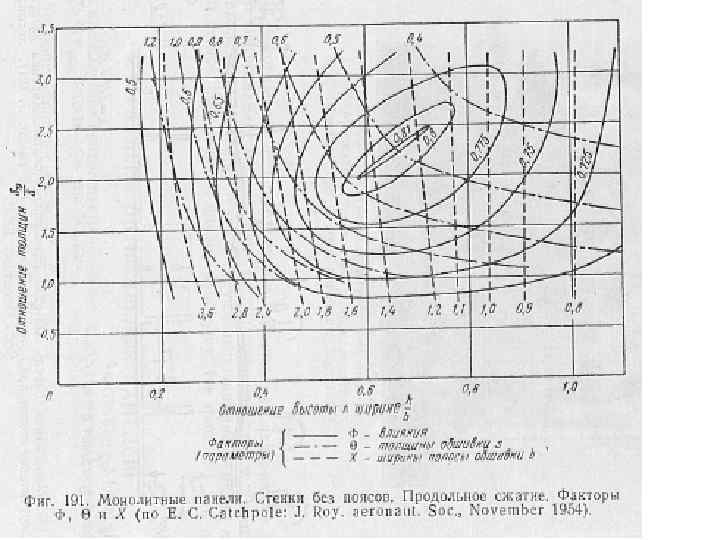
Назначение панелей. Панелью мы называем конструкцию, представляющую обшивку вместе с подкрепляющими её элементами. Панели встречаются во всех силовых агрегатах самолёта: в крыле, фюзеляже, в оперении, в агрегатах механизации крыла и других. Панели принимают на себя аэродинамическую и другие распределённые нагрузки, раздают их на элементы каркаса: нервюры, шпангоуты и лонжероны , и затем преобразуются с помощью этих элементов каркаса в изгибающие и крутящие моменты, которые опять же с помощью нервюр и лонжеронов преобразуют эти моменты в силы, которые растягивают или сжимают панели, а также в потоки касательных усилий, которые заставляют панели работать на сдвиг. Нижние панели крыла и верхние панели фюзеляжа работают в основном на растяжение и сдвиг. При расчете на прочность действующие напряжения следует умножить на коэффициент концентрации напряжений и сравнить их с предельными характеристиками материала : Чаще всего используют именно это значение для основных авиационных материалов. Этот коэффициент учитывает присутствие практически во всех элементах конструкции тех или иных концентраторов напряжений, получаемых в ходе производства намеренно или случайно. Это случайно просверленные отверстия, царапины, зарубки, заусенцы, микротрещины, рыхлоты, включения и многое другое. При проектировании растянутых панелей главное – обеспечение требований усталостной прочности и живучести. Для этого необходимо иметь достаточно низкие рабочие напряжения и всячески избегать концентрации напряжений или, во всяком случае, обеспечивать их минимальный уровень. Это достигается обеспечением плавных переходов толщин, введением максимально возможных радиусов скруглений, отсутствием наложения концентраторов друг на друга. В нижней панели крыла смотровые люки делают свободно плавающими, чтобы концентрация от отверстий под крепёж не накладывалась на концентратор по краю люка. Такая чувствительность панелей требует постоянного квалифицированного внимания ко всем местам конструкции, где определяющими являются переменные растягивающие напряжения.
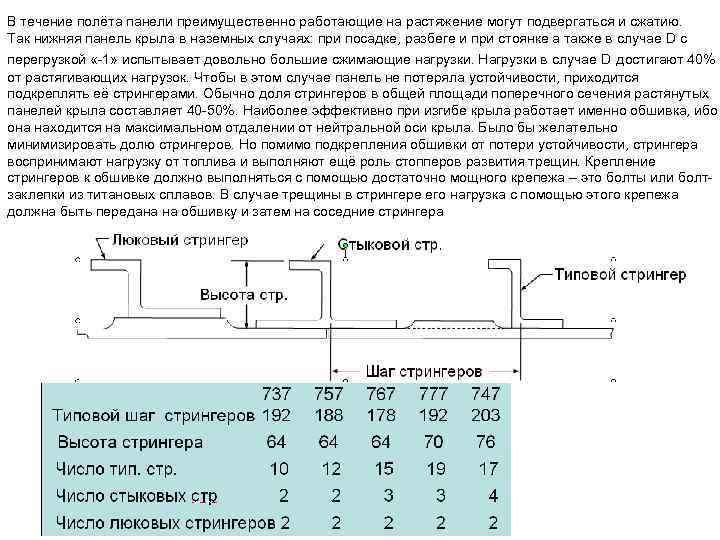
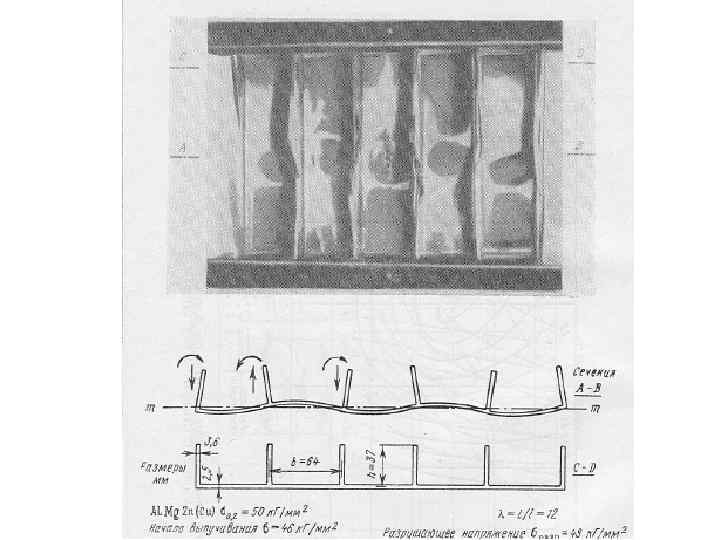
В течение полёта панели преимущественно работающие на растяжение могут подвергаться и сжатию. Так нижняя панель крыла в наземных случаях: при посадке, разбеге и при стоянке а также в случае D с перегрузкой «-1» испытывает довольно большие сжимающие нагрузки. Нагрузки в случае D достигают 40% от растягивающих нагрузок. Чтобы в этом случае панель не потеряла устойчивости, приходится подкреплять её стрингерами. Обычно доля стрингеров в общей площади поперечного сечения растянутых панелей крыла составляет 40 -50%. Наиболее эффективно при изгибе крыла работает именно обшивка, ибо она находится на максимальном отдалении от нейтральной оси крыла. Было бы желательно минимизировать долю стрингеров. Но помимо подкрепления обшивки от потери устойчивости, стрингера воспринимают нагрузку от топлива и выполняют ещё роль стопперов развития трещин. Крепление стрингеров к обшивке должно выполняться с помощью достаточно мощного крепежа – это болты или болтзаклепки из титановых сплавов. В случае трещины в стрингере его нагрузка с помощью этого крепежа должна быть передана на обшивку и затем на соседние стрингера
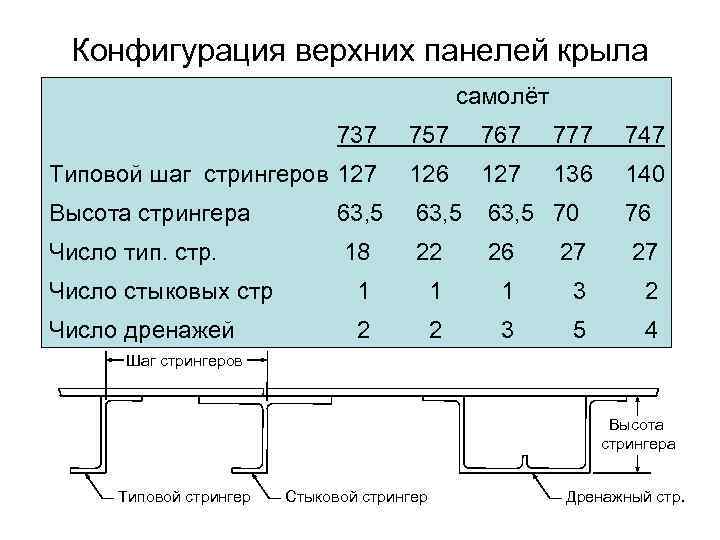
Конфигурация верхних панелей крыла самолёт 737 757 767 777 747 Типовой шаг стрингеров 127 126 127 136 140 Высота стрингера 63, 5 70 76 Число тип. стр. 18 22 26 27 27 Число стыковых стр 1 1 1 3 2 Число дренажей 2 2 3 5 4 Шаг стрингеров Высота стрингера Типовой стрингер Стыковой стрингер Дренажный стр.


Сжатые панели При проектировании сжатых панелей главное – обеспечение требований устойчивости. В этом случае требования статической прочности обеспечиваются автоматически. Сама по себе потеря устойчивости любого элемента конструкции не является критической. Если имеются параллельно работающие другие элементы, не потерявшие устойчивости, то разрушение конструкции не происходит. Верхняя панель крыла разрушается только если исчерпана несущая способность всех элементов, входящих в неё. При определении запасов прочности панель разбивается на элементы, состоящие из стрингера и обшивки или пояса лонжерона и обшивки. Такой элемент называют широкой стойкой. Рассматривается общая потеря устойчивости стрингера совместно с обшивкой(по Эйлеру) и местная форма потери устойчивости пластинок обшивки и элементов стрингера.
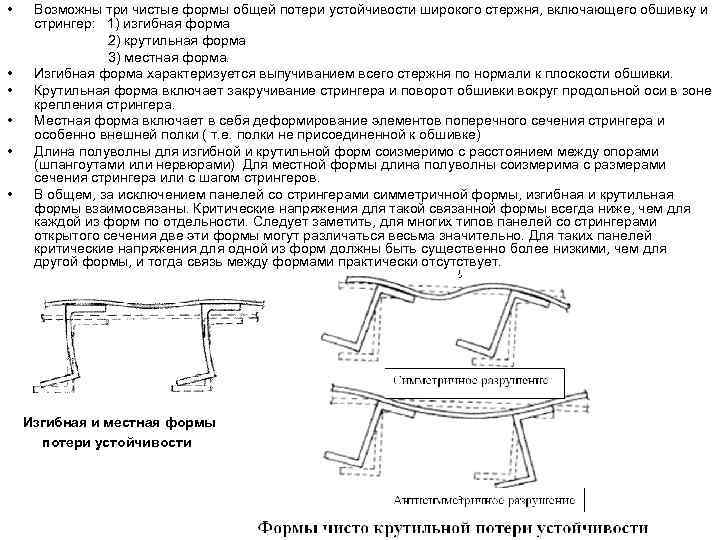
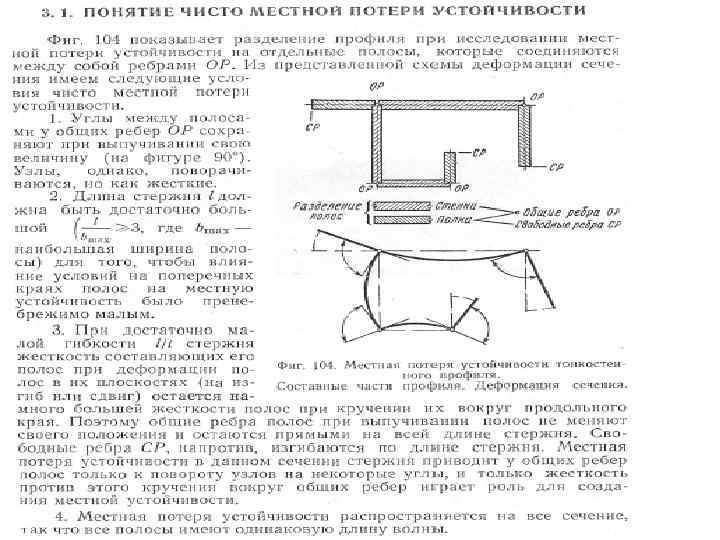
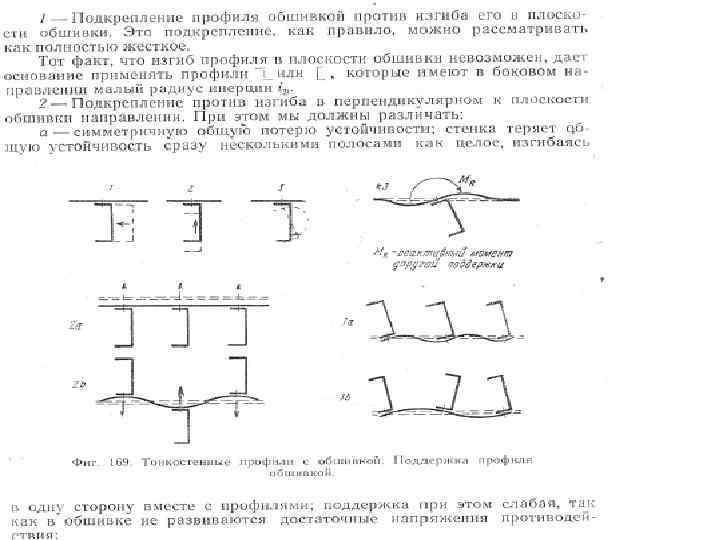
• • • Возможны три чистые формы общей потери устойчивости широкого стержня, включающего обшивку и стрингер: 1) изгибная форма 2) крутильная форма 3) местная форма. Изгибная форма характеризуется выпучиванием всего стержня по нормали к плоскости обшивки. Крутильная форма включает закручивание стрингера и поворот обшивки вокруг продольной оси в зоне крепления стрингера. Местная форма включает в себя деформирование элементов поперечного сечения стрингера и особенно внешней полки ( т. е. полки не присоединенной к обшивке) Длина полуволны для изгибной и крутильной форм соизмеримо с расстоянием между опорами (шпангоутами или нервюрами) Для местной формы длина полуволны соизмерима с размерами сечения стрингера или с шагом стрингеров. В общем, за исключением панелей со стрингерами симметричной формы, изгибная и крутильная формы взаимосвязаны. Критические напряжения для такой связанной формы всегда ниже, чем для каждой из форм по отдельности. Следует заметить, для многих типов панелей со стрингерами открытого сечения две эти формы могут различаться весьма значительно. Для таких панелей критические напряжения для одной из форм должны быть существенно более низкими, чем для другой формы, и тогда связь между формами практически отсутствует. Изгибная и местная формы потери устойчивости
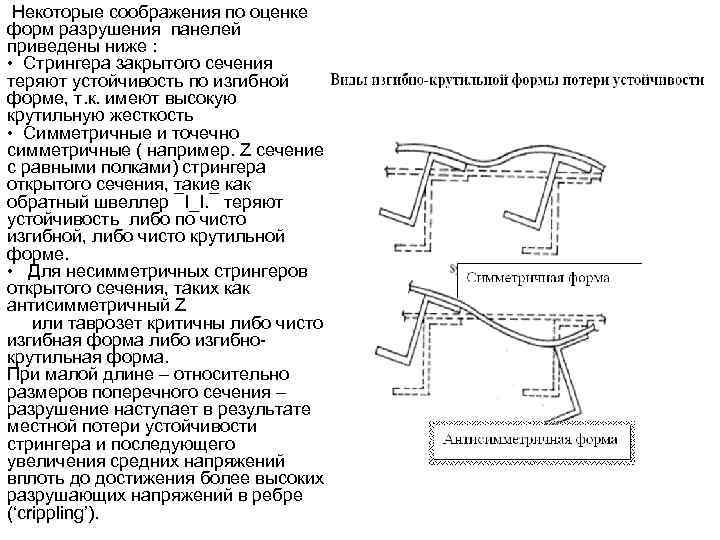
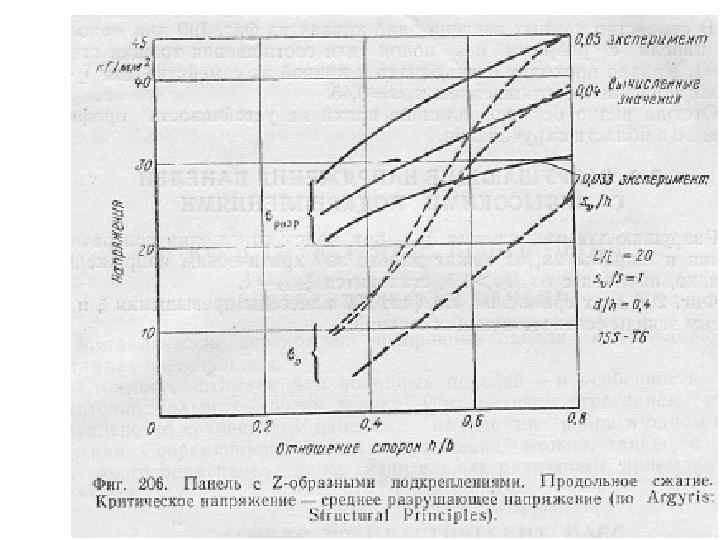
Некоторые соображения по оценке форм разрушения панелей приведены ниже : • Стрингера закрытого сечения теряют устойчивость по изгибной форме, т. к. имеют высокую крутильную жесткость • Симметричные и точечно симметричные ( например. Z сечение с равными полками) стрингера открытого сечения, такие как обратный швеллер ¯I_I. ¯ теряют устойчивость либо по чисто изгибной, либо чисто крутильной форме. • Для несимметричных стрингеров открытого сечения, таких как антисимметричный Z или таврозет критичны либо чисто изгибная форма либо изгибнокрутильная форма. При малой длине – относительно размеров поперечного сечения – разрушение наступает в результате местной потери устойчивости стрингера и последующего увеличения средних напряжений вплоть до достижения более высоких разрушающих напряжений в ребре (‘crippling’).
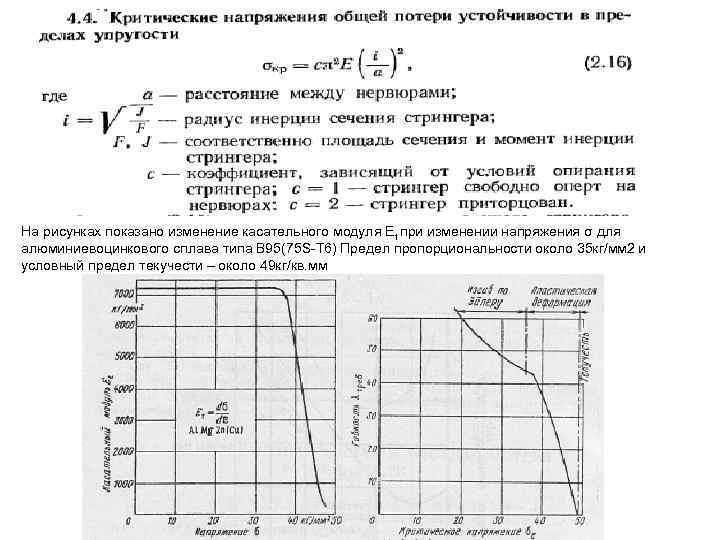
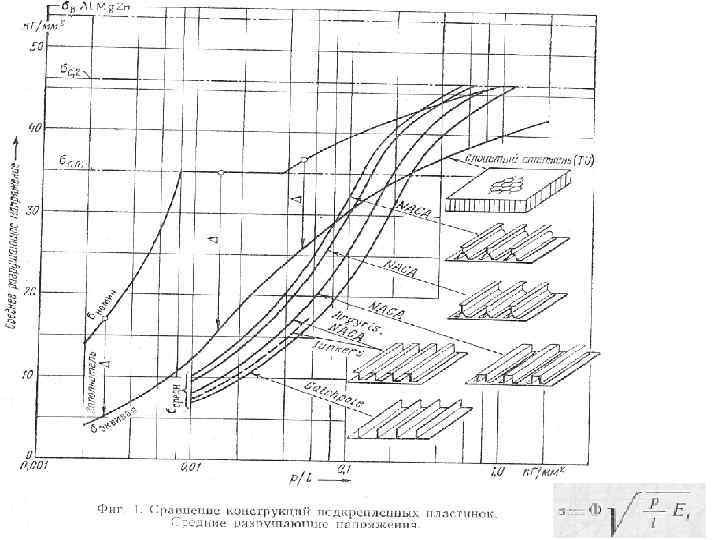
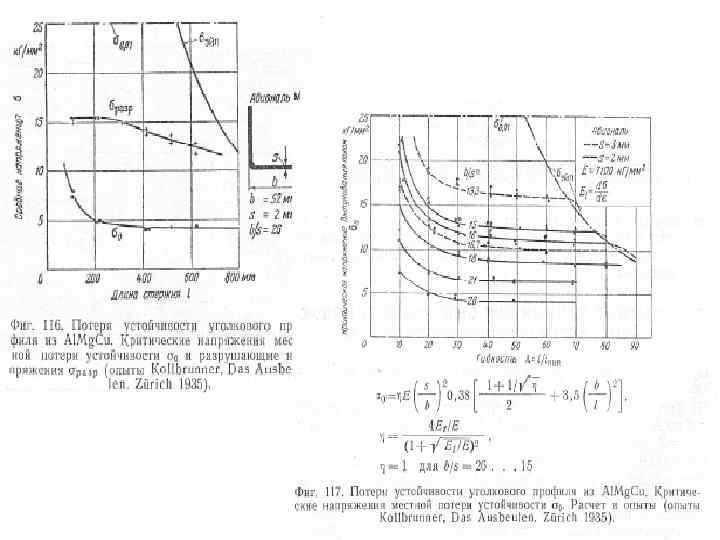
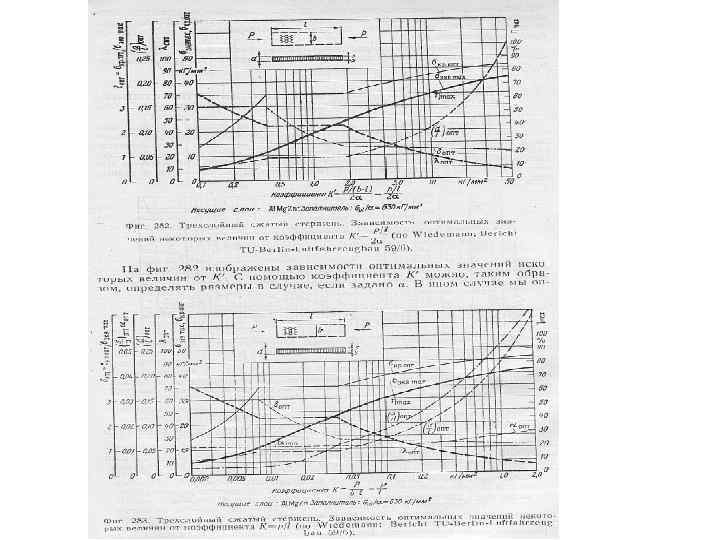
На рисунках показано изменение касательного модуля Еt при изменении напряжения σ для алюминиевоцинкового сплава типа В 95(75 S-T 6) Предел пропорциональности около 35 кг/мм 2 и условный предел текучести – около 49 кг/кв. мм

Note: See also Gere & Timoshenko, Mechanics of Materials, PWS, 1984, Chapter 9
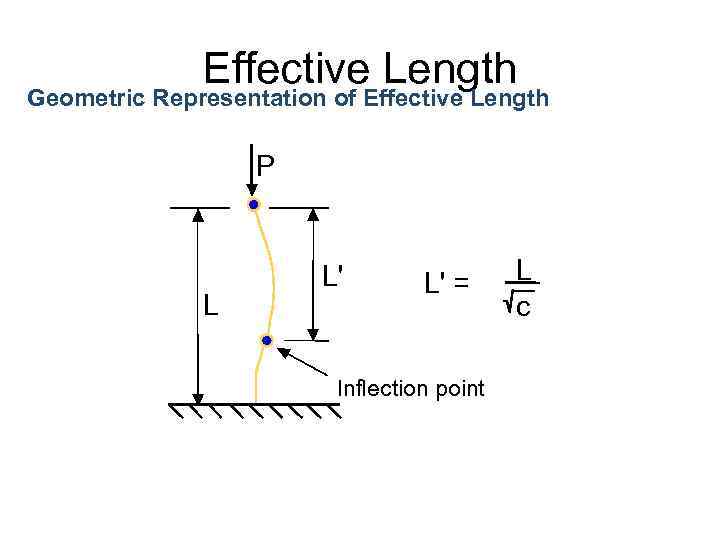
Effective Length Geometric Representation of Effective Length P L L’ L’ = Inflection point L c
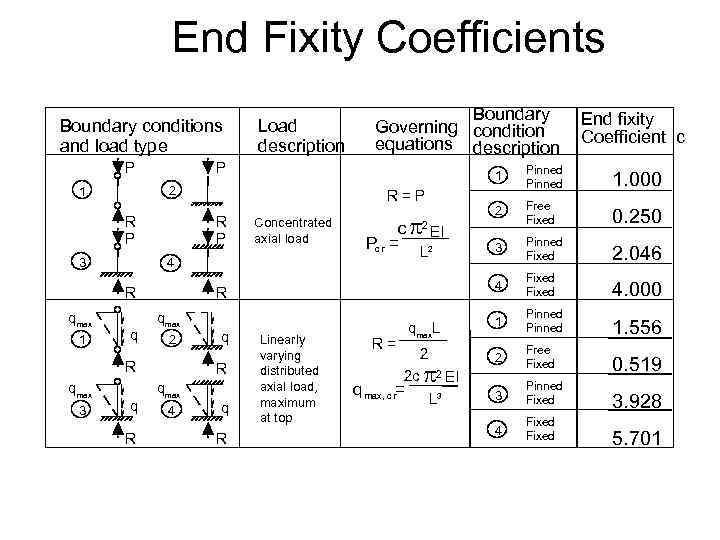
End Fixity Coefficients Boundary conditions and load type P P R P 3 1 q 3 q R 2 Free Fixed 0. 250 3 Pinned Fixed 2. 046 Fixed 4. 000 q max. L 1 Pinned 1. 556 2 2 Free Fixed 0. 519 3 Pinned Fixed 3. 928 4 Fixed c 2 EI Pc r = L 2 R q max 1. 000 4 Concentrated axial load 4 R Pinned R=P R P q R q max 4 q R End fixity Coefficient c 1 2 1 q max Load description Boundary Governing condition equations description Linearly varying distributed axial load, maximum at top R= 2 c q max, c r= 2 EI L 3 5. 701
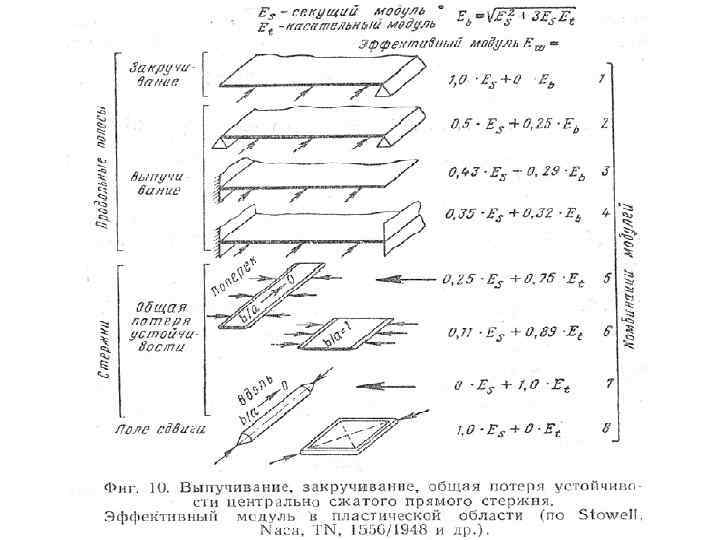

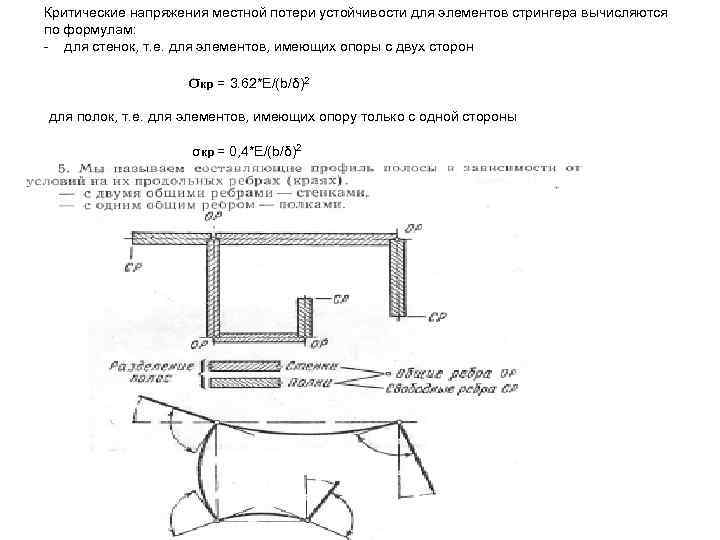
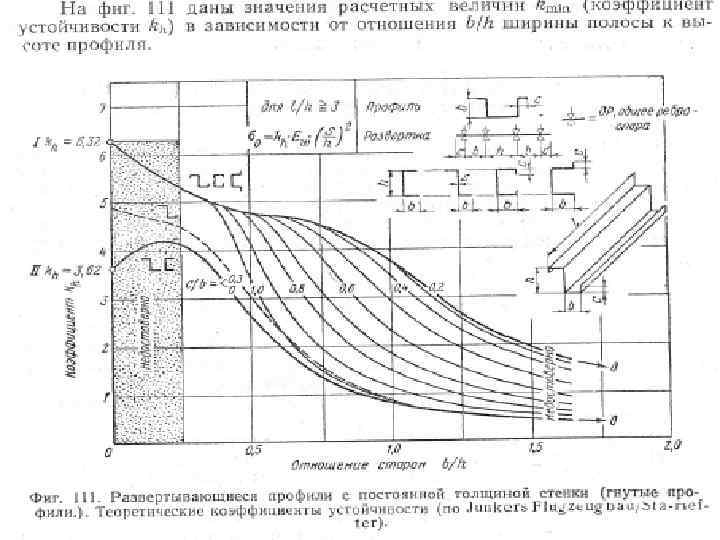
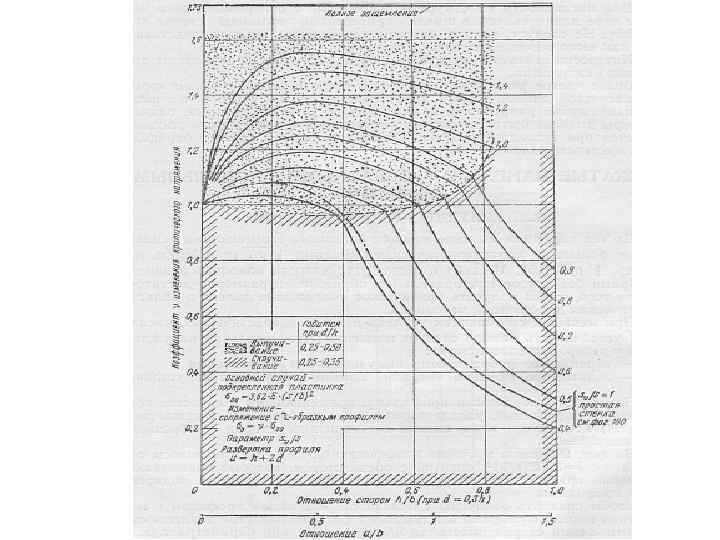
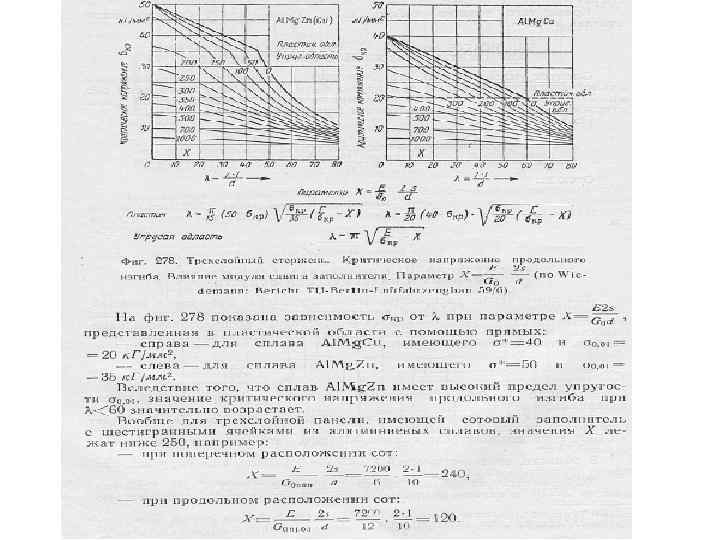
Критические напряжения местной потери устойчивости для элементов стрингера вычисляются по формулам: — для стенок, т. е. для элементов, имеющих опоры с двух сторон σкр = 3. 62*E/(b/δ)2 для полок, т. е. для элементов, имеющих опору только с одной стороны σкр = 0, 4*E/(b/δ)2

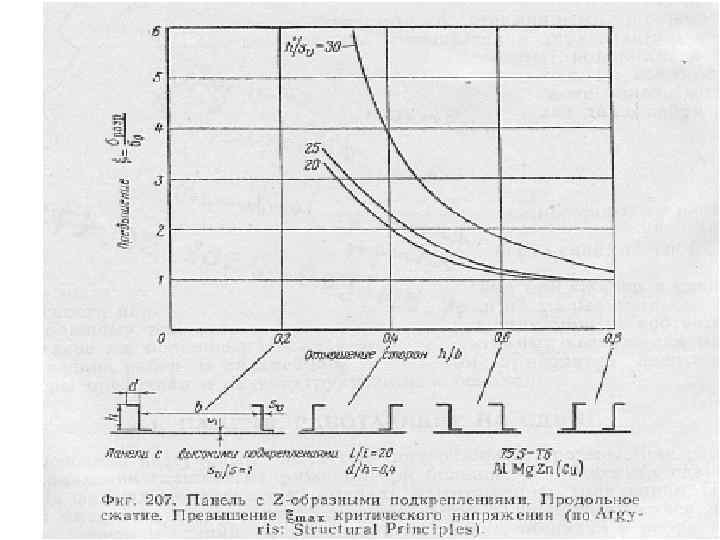
Помимо критических напряжений потери устойчивости элементарных пластинок, составляющих стрингер, можно определить разрушающие напряжения для каждого элемента стрингера, имея в виду, что после потери устойчивости средние напряжения пластинки растут до тех пор, пока напряжения в ребре, окантовывающем пластинку не достигнут предельного значения(эффект Кармана). В качестве предельного напряжения в ребре принимается либо критическое напряжение общей потери устойчивости широкой стойки, либо разрушающее напряжения сжатия для материала σв сж Уравнение Кармана для предельного напряжения элемента стрингера выглядит так: σпред=√ σкр σв Точно также определяется предельное разрушающее напряжение для обшивки σпред обш =√ σкр σстр Здесь под σстр понимается разрушающее напряжение стрингера, которое равно минимуму из двух либо критическому напряжению общей потери устойчивости широкой стойки, либо минимальному значению предельного напряжения элемента стрингера – берётся самый слабый элемент стрингера. Если обшивка теряет устойчивость между заклёпками, то вместо σстр в подкоренное выражение подставляется критическое напряжение местной потери устойчивости обшивки между заклёпками, которое определяется из следующего уравнения: σкр мз = 0, 9*Е/((t-d)/δ)2. Здесь Е-модуль упругости материала обшивки, t – шаг заклёпок, d- диаметр заклёпок, δ-толщина обшивки. В качестве σкр для обшивки принимается критическое напряжение местной потери устойчивости обшивки с учетом поперечных и сдвигающих напряжений. Далее предельное напряжение обшивки умножается на площадь поперечного сечения обшивки, предельное напряжение стрингера умножается на площадь поперечного сечения стрингера. Так мы можем получить предельную разрушающую нагрузку широкой стойки, т. е. разрушающую силу элемента панели при сжатии. Сравнив её с действующей нагрузкой, мы можем получить запас прочности или избыток прочности.

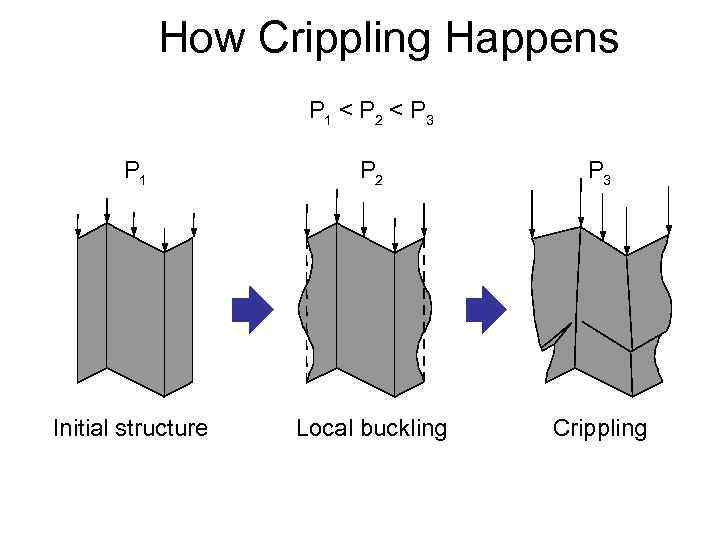
How Crippling Happens P 1

σкр=3, 62*E/(b/δ)2 τкр=5*E/(b/δ)2 σ/σкр+(τ/τкр)2=1 2. 2 2. 3


















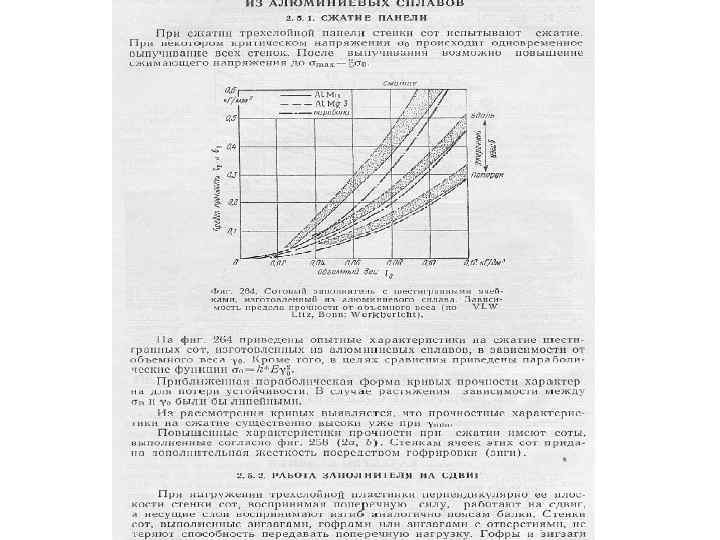
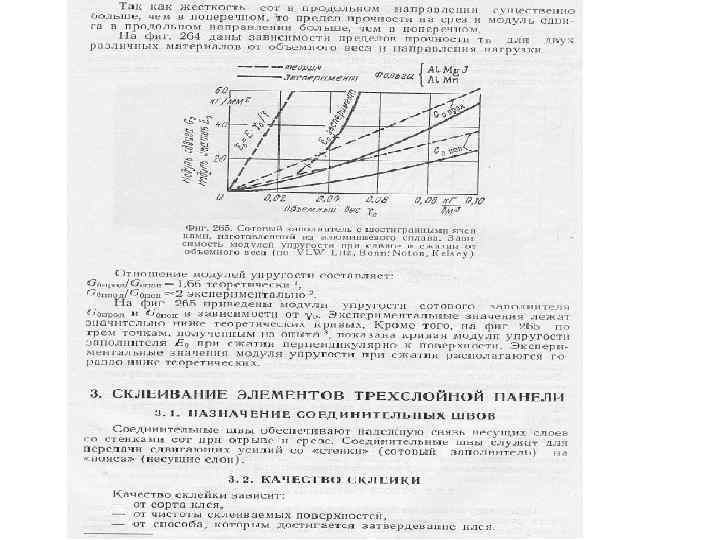
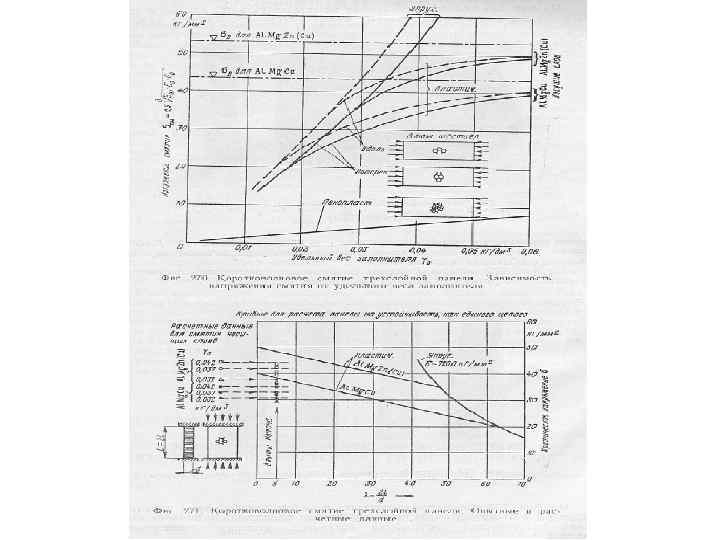
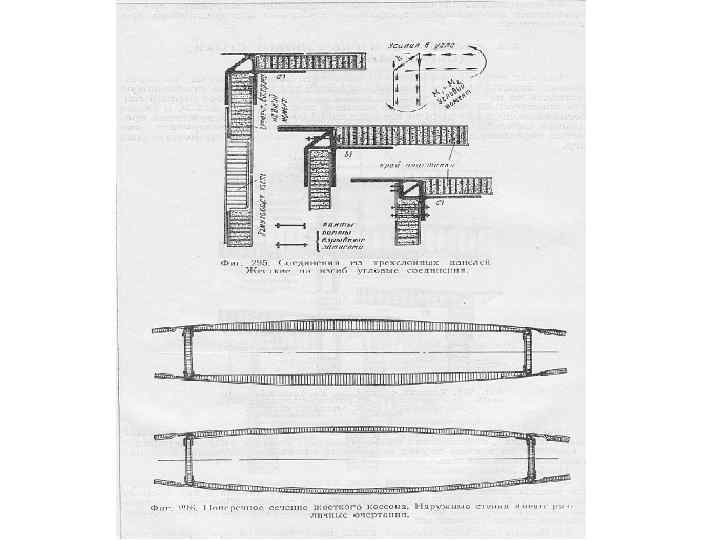
Сотовые панели
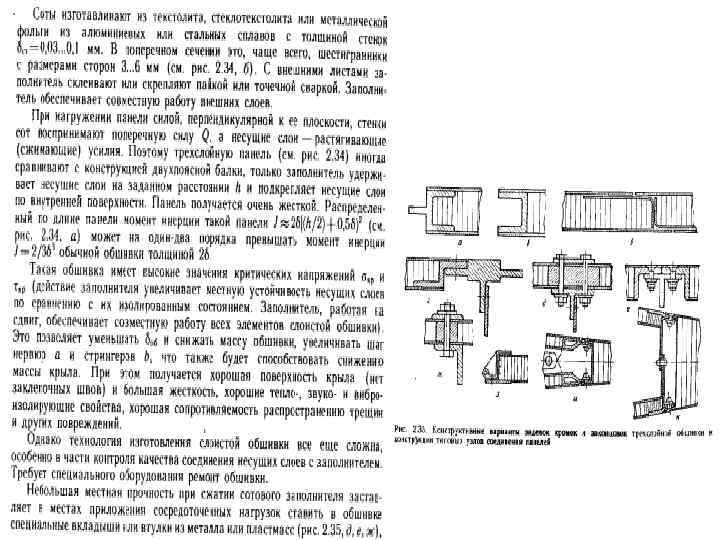

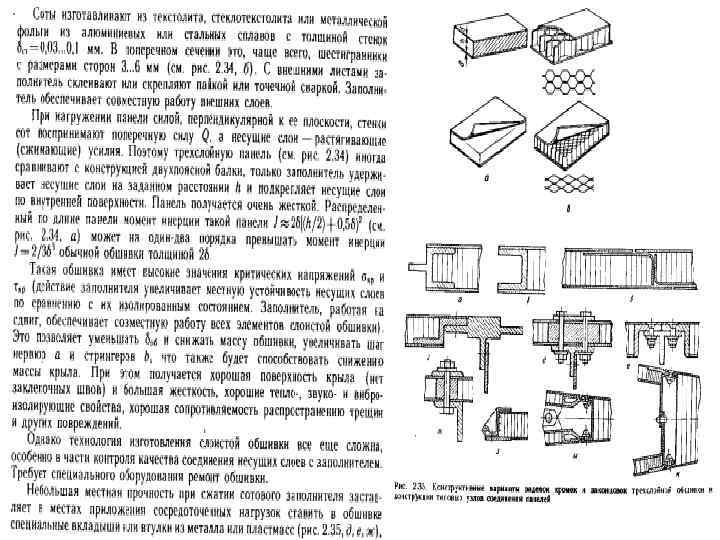

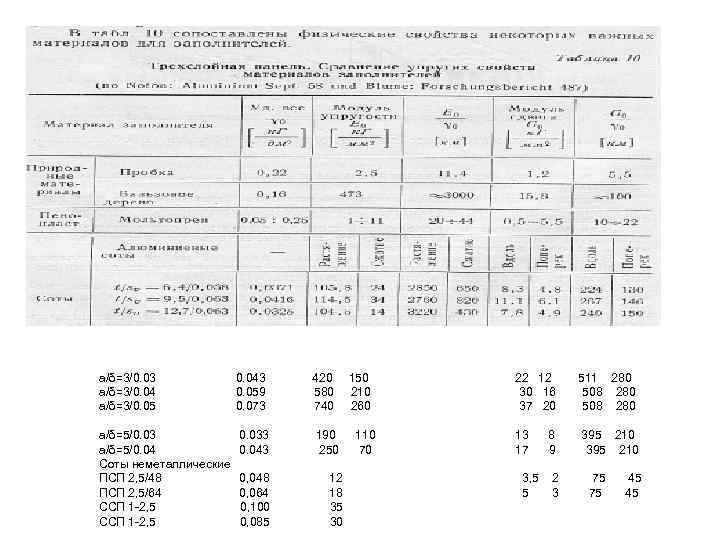
a/δ=3/0. 03 a/δ=3/0. 04 a/δ=3/0. 05 0. 043 0. 059 0. 073 420 580 740 a/δ=5/0. 03 a/δ=5/0. 04 Соты неметаллические ПСП 2, 5/48 ПСП 2, 5/64 ССП 1 -2, 5 0. 033 0. 043 190 250 0, 048 0, 064 0, 100 0, 085 12 18 35 30 150 210 260 110 70 22 12 30 16 37 20 511 280 508 280 13 17 395 210 3, 5 5 8 9 2 3 75 75 45 45


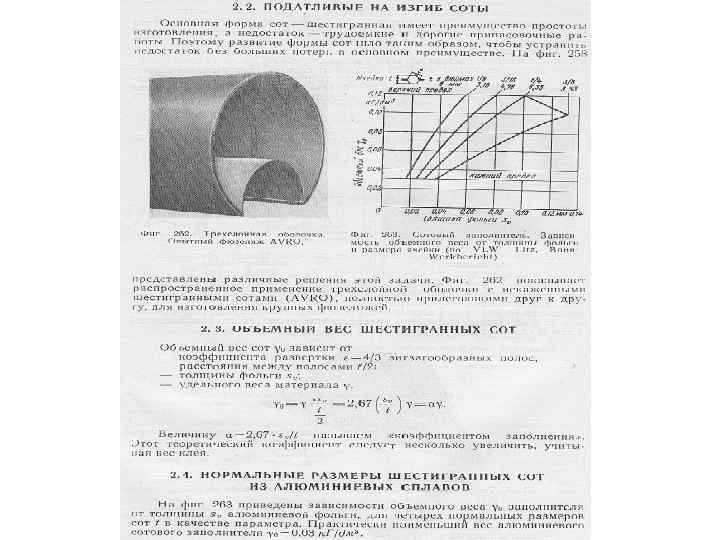











Источник
