Расчет кладки на растяжение
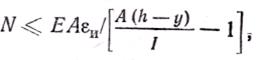
Расчет изгибаемых элементов каменных конструкций выполняется только для перевязанных сечений. Работа кладки на изгиб по неперевязанному сечению не допускается. Изгибу подвержены подпорные стенки и стены подвалов, находящиеся под давлением грунта, простенки, испытывающие воздействия от собственного веса и давления ветра, а также некоторые другие конструкции. При изгибе в поперечном сечении элемента действуют два внутренних силовых фактора: изгибающий момент и поперечная сила, причем кладка считается упругим материалом.
Несущая способность при изгибе определяется по формулам сопротивления материалов. Расчетная формула при действии изгибающих моментов имеет следующий вид:
M<RtbW, (19.23)
здесь Rtb— расчетное сопротивление кладки растяжению при изгибе по перевязанному сечению; W — упругий момент сопротивления кладки.
Несущую способность сечения при действии поперечной силы определяют по сопротивлению кладки главным растягивающим напряжениям по наклонному сечению и вычисляют по следующей формуле:
Q<Rtwbz, (19.24)
где Rtw— расчетное сопротивление кладки главным растягивающим напряжениям при изгибе; b — ширина сечения (толщина стены); z — плечо внутренней пары сил, для прямоугольного сечения z= (2/3) h ≈ 0,67h.
Центральное растяжение наблюдается в стенах круглых резервуаров, силосов и других емкостей. Расчет ведут по перевязанному сечению, так как проектировать и возводить конструкции, в которых возможна работа каменной кладки на растяжение по неперевязанному сечению, не разрешается. Условие расчета по первой группе предельных состояний имеет следующий вид:
N<Rt An, (19.25)
где N — расчетная сила при осевом растяжении; Rt— расчетное сопротивление каменной кладки растяжению по перевязанному сечению; Ап— расчетная площадь сечения нетто (за вычетом площади вертикальных швов).
Работа на срез по горизонтальным швам элементов каменных конструкций возможна в подпорных стенах и стенах подвалов, а также в опорных зонах изгибаемых конструкций, где действуют значительные поперечные силы. Сопротивление срезу (сдвигу) определяется касательным сцеплением раствора с камнем и силой трения камня по шву, зависящих от веса лежащей выше части кладки.
Условие расчета каменной кладки по неперевязанному сечению и перевязанным швам бутовой кладки на срез имеет вид
(19.26)
где Rsg— расчетное сопротивление кладки на срез по неперевязанному сечению; 0,8 — поправочный коэффициент, учитывающий уменьшение сил трения из-за возможного увлажнения швов и других неблагоприятных условий работы; n — коэффициент, учитывающий тип кладки (для сплошного кирпича и камней n=1, пустотелого — n=0,5);
μ — коэффициент трения камня по шву (для кирпичной кладки μ =0,7); σ0=N/A — среднее напряжение сжатия в расчетном горизонтальном шве кладки (N — наименьшее расчетное усилие от собственного веса расположенного выше участка кладки, вычисленное с учетом коэффициента надежности по нагрузке γf=0,9); A — площадь рассчитываемого сечения.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. От каких факторов зависит прочность каменной кладки?
2. Перечислите стадии работы кладки при осевом сжатии.
3. Как определяется прочность кладки?
4. Укажите деформативные свойства кладки, назначение модуля деформации.
5. Какова прочность кладки при растяжении, срезе и изгибе?
6. Как выполняется расчет каменных конструкций по предельным состояниям?
7. Как выполняется расчет по второй группе предельных состояний (деформациям и раскрытию трещин)?
8. Как выполняется расчет элементов каменных конструкций
при центральном сжатии?
9. Как определяется гибкость и оценивается ее влияние на несущую способность cжатых элементов?
10.Каким образом учитывается влияние длительности действия внешней нагрузки на несущую способность кладки?
11.Как производится расчет каменных конструкций при местном сжатии?
12.Каким образом рассчитывают внецентренно сжатые элементы из каменной кладки?
13.Как выполняется расчет каменной кладки, работающей на изгиб, растяжение и срез?
Глава 20. Армированные каменные конструкции
Источник
Расчет неармированных элементов по деформациям
Задачей расчета по деформациям является ограничение деформаций конструкций, поддерживающих кладку такими пределами, которые гарантируют от появления в ней трещин, недопустимых по условиям эксплуатации.
Рассмотрим определение расчетных предельных деформаций для случая, когда каменная кладка в самонесущей стене передает горизонтальную нагрузку, действующую перпендикулярно плоскости стены, на каркас. При этом введем следующие допущения:
а) вся горизонтальная нагрузка передается только каркасу, работе которого кладка стены не помогает;
б) деформации кладки полностью следуют за деформациями каркаса.
Прежде всего, необходимо установить, какие расчетные предельные деформации могут быть приняты для рассматриваемой самонесущей стены. По-видимому, прогибы и углы поворота любых сечений стены должны быть такими, чтобы возникающие при этом в кладке стены максимальные деформации растяжения не превышали определенного, установленного опытами максимума. Деформации растяжения в кладке можно определить, исходя из условия одинакового радиуса кривизны стены ρк и поддерживающей конструкции ρ.
Относительные деформации кладки ξ на растянутой грани, слагающиеся из деформаций растяжения при изгибе ξи и деформаций сжатия ξ0 от собственного веса степы и других вертикальных нагрузок, не должны превышать величин предельных деформаций ξпр, приведенных в нормах проектирования.
В том же случае, когда предъявляются повышенные требования в отношении недопустимости появления трещин на растянутой поверхности стен (при наличии гидроизоляционных штукатурок и т. д.), относительные деформации ξпр нормами устанавливаются меньшими, чем указано в табл. 1. Таким образом, расчет по деформациям самонесущей стены сводится к обеспечению условия
ξ = ξи – ξ0 ≤ ξпр. (1)
Величины ξи (см. рис.64,в) и ξ0 приближенно определяются по формулам сопротивления упругих материалов, согласно которым.
ξи= (a – y) /ρ = (Mн (a — y)) /EJ; (2)
ξ0 = Nнк /EкFк, (3)
где Mн — изгибающий момент в элементе каркаса от нормативных нагрузок;
EJ — жесткость (произведение модуля упругости на момент инерции) каркаса при изгибе; а — у — расстояние от центра тяжести сечения кладки стены до растянутой грани;
Nнк — продольная сила сжатия в кладке стены от нормативных нагрузок;
Eк , Fк и Jк — модуль деформаций кладки, площадь и момент инерции поперёчного сечения кладки. При проверке деформаций в горизонтальной плоскости при изгибе между стойками каркаса Nнк = 0 и, следовательно ξ0= 6.
Рис. 1. Схемы к расчету самонесущих стен по деформациям
(а — опирание стен на вертикальные опоры; б — то же, но на горизонтальную опору; в — схема к формуле (2);
г и д — к определению М0и М1при расчете самонесущей стены с одной горизонтальной опорой;
1 — самонесущая стена; 2 — стойка каркаса; 3 — горизонтальная связь; 4 — ветровая ферма каркаса)
Кроме расчета по деформациям, должна быть проверена прочность самонесущих стен (расчет по первому предельному состоянию); при этом наряду с нагрузками, непосредственно приложенными к стене, необходимо учитывать дополнительные изгибающие моменты, возникающие в ней при изгибе каркаса.
Таблица 1
| Вид деформаций кладки | Предельные относительные деформации кладки ξпр при степени долговенчости зданий | |
| I | II | |
| Сжатие | 0.4/α | 0.5/α |
| растяжение осевое и при изгибе по перевязанному сечению | 1.5×10-4 | 2×10-4 |
| то же, по неперевязанному сечению | 0.8×10-4 | 1×10-4 |
В случае если стена связана анкерами только с вертикальными элементами (стойками) каркаса (рис.1,а), то дополнительным момент может быть учтен введением в направлении прогиба стены эксцентрицитета ео.д к расчетной продольном силе Nк возникающей в стене от собственного веса и других нагрузок. Если Nк приложена к стене с эксцентрицитетом от внецентренно приложенных вертикальных нагрузок, то последний увеличивается на величину ео.д.
Величину эксцентрицитета ео.д определим, исходя из таких соображений. Нормативный изгибающий момент в кладке каменных конструкций Мнк при радиусе кривизны стены ρк может быть найден по формуле
Мнк = EкJк/ρк . (4)
Ранее мы приняли, что радиусы кривизны элемента каркаса ρ и кладки ρк равны, тогда, воспользовавшись формулой (2), согласно которой ρ = ρк = (a – y)/ξн и подставив это значение в (4), получим
Мнк = (ξиEкJк)/(a – y), (5)
или, переходя от нормативных значений к расчетным:
Мк = (nиξиEкJк)/(a – y), (6)
где Мк — расчетный изгибающий момент в кладке, возникающий при изгибе каркаса;
пи — коэффициент перегрузки для нагрузки, вызывающей изгиб.
Пользуясь формулой (3) и также переходя к расчетным значениям, найдем расчетную продольную силу в стене
Nк = n0ξ0EкFк, (7)
где п0 — коэффициент перегрузки для нагрузки, вызывающей сжатие кладки.
Из формулы (6), учтя, что радиус инерции горизонтального сечения стены, получим
eо.д = Мк/Nк = nиξиr2к/ n0ξ0 (a – y). (8)
Расчет армированных элементов по деформациям
Расчет по деформациям армированных элементов производится по тем же формулам, что и неармированной кладки. При этом упругая характеристика кладки определяется по формуле (αа.с = α/1+3рс).
Если относительные деформации растяжения ξ оказываются больше ξпр, т.е., если условие (1) не удовлетворено, то для повышения ξпр может быть или увеличена жесткость каркаса, или кладка должна быть усилена продольной арматурой. Если процент продольного армирования р ≥ 0,03, то относительные предельные деформации растяжения ξпр по табл. 1 могут быть увеличены на 25%. Модуль деформации продольно армированной кладки принимается по формуле (E = 0,8αRна.к).
При относительных деформациях кладки ξ>1,25 ξпр продольное армирование стены назначается, исходя из расчета по прочности, с учетом эксцентрицитета ео.д ,найденного в предыдущем параграфе.
Источник
Продолжение статьи Расчет кирпичной кладки на прочность.
Пример расчета кирпичной стены по сечению II-II.
Исходные данные: Рассчитать наружную стену первого этажа двухэтажного коттеджа на прочность. Стены выполнены из кирпича М75 на растворе М25 толщиной h=250мм, длина стены L=6м. Высота этажа H=3м. Нагрузка от перекрытия первого этажа P1=1,8т. Нагрузка от вышележащих этажей G=3,8т. Длительная продольная сила Ng=4,563т. Все нагрузки собраны в статье Сбор нагрузок на стену первого этажа для сечения I-I на один погонный метр кладки.
Решение.

Рассмотрим сечение II-II.
В данном случае для определения продольной силы NII нужно дополнительно учесть вес кладки первого этажа (G1), расположенной между сечением I-I и II-II.
G1 = 1/3 (ρ*h*L*H) = 1/3 (1800*0,25*1*3 )= 450кг = 0,45т
ρ — плотность кладки, 1800 кг/м3
h — толщина стены, 0,25 м
L — длина одного погонного метра стены, 1 м
H — высота этажа, 3 м
Тогда продольная сила NII будет равна:
NII = N + G1 = 5,5т + 0,45т = 5,95 т
Так как сечение II-II находится на расстоянии 2/3 высоты H, то изгибающий момент от перекрытия будет равен:
МII = 2М / 3
М = 13,5 т*см (смотрим предыдущую статью)
МII = 2*13,5 / 3 =9 т*см
Эксцентриситет продольной силы NII в сечении II-II составит:
e0 II = MII / NII = 9 / 5,95 = 1,5 см
Общий эксцентриситет с учетом случайного:
e0 II = 1,5 + 2 = 3,5 см
y = h / 2 = 12,5 см
При e0 II = 3,5 см < 0,7y = 8,75 см расчет по раскрытию трещин в швах кладки можно не производить.
Прочность кладки внецентренно сжатого элемента определяется по формуле:
NII ≤ mg φ1 R Ac ω
— R — расчетное сопротивление кладки сжатию. Определяем по таблице 2 СНиП II-22-81 (скачать СНиП II-22-81). Расчетное сопротивление кладки из кирпича М75 на растворе М25 равно 11 кг/см2 или 110 т/м2
— Ac — площадь сжатой части сечения, определяется по формуле:
A — площадь поперечного сечения одного погонного метра кладки. A = L*h = 1*0,25 = 0,25 м2
Ac = 0,25 (1 — 2*0,035 / 0,25) = 0,18 м2
— ω — коэффициент, определяемый по формуле:
ω = 1 + e0 II / h = 1 + 0,035 / 0,25 = 1,14 ≤ 1,45 условие выполняется
Для сечения II-II необходимо дополнительно определить коэффициенты mg и φ1, так как в этом сечении они не будут равны единице.
— φ1 — коэффициент продольного изгиба:
φ1 = (φ + φс) / 2
Для определения коэффициента продольного изгиба элемента для всего сечения φ и сжатого сечения φс, необходимо определить гибкость элемента λh и гибкость сжатой части сечения λhс , а также упругую характеристику кладки α в сечении II-II.
λh = 2l0 / 3h
l0= H =3 м
λh = 2H / 3h = 2*3 / 3*0,25 = 8
λhс = 2H / 3hc =2Н / 3(h — 2*e0II) = 2*3 / 3*(0,25 — 2*0,035) = 11
Упругая характеристика α принимается по таблице 15 п.7 СНиП II-22-81 и равна 1000.
По таблице ниже:
Гибкость | Коэффициент продольного изгиба при упругих характеристиках кладки, α | |||||||
λh | λi | 1500 | 1000 | 750 | 500 | 350 | 200 | 100 |
4 6 8 10 12 14 16 18 22 26 30 34 38 42 46 50 54 | 14 21 28 35 42 49 56 63 76 90 104 118 132 146 160 173 187 | 1 0,98 0,95 0,92 0,88 0,85 0,81 0,77 0,69 0,61 0,53 0,44 0,36 0,29 0,21 0,17 0,13 | 1 0,96 0,92 0,88 0,84 0,79 0,74 0,7 0,61 0,52 0,45 0,38 0,31 0,25 0,18 0,15 0,12 | 1 0,95 0,9 0,84 0,79 0,73 0,68 0,63 0,53 0,45 0,39 0,32 0,26 0,21 0,16 0,13 0,1 | 0,98 0,91 0,85 0,79 0,72 0,66 0,59 0,53 0,43 0,36 0,32 0,26 0,21 0,17 0,13 0,1 0,08 | 0,94 0,88 0,8 0,72 0,64 0,57 0,5 0,45 0,35 0,29 0,25 0,21 0,17 0,14 0,1 0,08 0,06 | 0,9 0,81 0,7 0,6 0,51 0,43 0,37 0,32 0,24 0,2 0,17 0,14 0,12 0,09 0,07 0,05 0,04 | 0,82 0,68 0,54 0,43 0,34 0,28 0,23 _ _ _ _ _ _ _ _ _ _ |
Примечания: Коэффициент при промежуточных величинах гибкостей определяется по интерполяции. | ||||||||
определяем φ = 0,92 и φс = 0,86 (φс определили интерполяцией)
φ1 = (φ + φс) / 2 = (0,92 + 0,86) / 2 = 0,89
— mg определяется по формуле:
Ng — длительная продольная сила (постоянные + временные длительные).
В статье Сбор нагрузок мы определили значение Ng = 4,563 т в сечении I-I. Для того, чтобы вычислить значение длительной продольной силы в сечении II-II (Ng II) необходимо прибавить вес кладки между двумя сечениями, которая равна G1 = 0,45 т.
Тогда,
Ng II = 4,563 + 0,45 = 5,013 т.
e0g — эксцентриситет от длительной продольной силы, который в сечении II-II будет равен:
e0g II = MII / Ng II = 9 / 5,013 = 1,8 см
Общий эксцентриситет длительной продольной силы с учетом случайного:
e0g II = 1,8 + 2 = 3,8 см
η — коэффициент при λhс = 11, принимаемый по таблице:
Гибкость | Коэффициент η для кладки | |||||
λh | λi | из глиняного кирпича и керамических камней; из камней и крупных блоков из тяжелого бетона; из природных камней всех видов | из силикатного кирпича и силикатных камней; камней из бетона на пористых заполнителях; крупных блоков из ячеистого бетона | |||
при проценте продольного армирования | ||||||
0,1 и менее | 0,3 и более | 0,1 и менее | 0,3 и более | |||
≤10 12 14 16 18 20 22 24 26 | ≤35 42 49 56 63 70 76 83 90 | 0,04 0,08 0,12 0,15 0,20 0,24 0,27 0,31 | 0,03 0,07 0,09 0,13 0,16 0,20 0,23 0,26 | 0,05 0,09 0,14 0,19 0,24 0,29 0,33 0,38 | 0,03 0,08 0,11 0,15 0,19 0,22 0,26 0,30 | |
Примечание. Для неармированной кладки значения коэффициента η следует принимать как для кладки с армированием 0,1 % и менее. При проценте армирования более 0,1 и менее 0,3 коэффициент η определяется интерполяцией. | ||||||
η = 0,02 (определен интерполяцией)
mg = 1 — 0,02*(5,013 / 5,95)*(1 + 1,2*3,8 / 25) = 0,98
Несущая способность кладки равна:
NII ≤ 0,98 * 0,89 * 110 * 0,18 * 1,14 = 19,7 т
5,95 ≤ 19,7
Прочность кладки обеспечена.
Статья была для Вас полезной?
Оставьте свой отзыв в комментарии
Источник
РАСЧЕТ ЭЛЕМЕНТОВ КАМЕННЫХ КОНСТРУКЦИЙ
Предельные состояния и особенности расчета
● Расчет каменных и армокаменных конструкций ведут по методу предельных состояний. При этом учитывают две группы предельных состояний: первая — по несущей способности (прочности и устойчивости), вторая — по образованию и раскрытию трещин и по деформациям. Расчет по первой группе выполняют всегда и для всех видов конструкций. Расчет по второй группе выполняют для конструкций, где не допускаются трещины (облицовка резервуаров) или требуется ограничение их раскрытия (внецентренно сжатые элементы с большими эксцентриситетами), ограничиваются деформации по условиям совместной работы смежных конструкций (стеновые заполнения каркасов зданий) и др. Целью расчета являются подбор сечений элементов конструкций или проверка имеющихся сечений. Вычисленные напряжения, деформации и ширина раскрытия трещин не должны превышать предельных значений, установленных в [5]. Расчет по несущей способности производят из условия, что расчетное усилие F меньше или равно расчетной несущей способности элемента Fu. Расчетное усилие вычисляют при действии нагрузок, взятых с коэффициентом надежности по нагрузке γf (см. гл. 2) при неблагоприятном их сочетании. Расчетную несущую способность определяют в зависимости от геометрических размеров сечения, расчетного сопротивления кладки R и коэффициентов условий работы. Расчетное сопротивление, учитывающее возможность снижения прочности, связанное с естественным разбросом механических свойств, учитывается коэффициентом надежности γ и определяется по формуле R=Ru/γ, где Ru — временное сопротивление кладки; γ — принимается для всех видов кладок, работающих на сжатие, равным 2, на растяжение — 2,25. Другие обстоятельства, влияющие на несущую способность и деформативность, учитываются коэффициентом условий работы γс, на который умножается величина R. Например, при расчете прочности каменных и армокаменных конструкций площадью сечения 0,3 м2 и менее расчетное сопротивление умножается на γc = 0,8.
Расчет неармированных конструкций
■ Расчет прочности центрально-сжатых элементов.
Расчет неармированных центрально-сжатых элементов по несущей способности производят в предположении равномерного распределения напряжений по сечению по формуле (рис. 17.1, а)
где N — расчетная продольная сила; mg — коэффициент снижении несущей способности вследствие ползучести кладки, определяемый по формуле (17.3) при e0g=0; φ — коэффициент, учитывающий снижение несущей способности элемента за счет продольного изгиба, зависящий от гибкости элемента λ и упругой характеристики кладки α; R — расчетное сопротивление кладки сжатию; А — площадь поперечного сечения элемента.
●Гибкость элемента любой формы представляет собой отношение расчетной длины к радиусу инерции сечения λi = l0/i, а прямоугольного сечения λh = l0/h, где h — наименьший размер сечения.
В элементах, имеющих неподвижные горизонтальные опоры (в стенах и столбах многоэтажных зданий), расчетная длина l0 равна их фактической длине — высоте этажа H; в элементах, имеющих упругую верхнюю опору (стенах и столбах одноэтажных промзданий), l0=1,25 Н для многопролетных зданий; l0=1,5 H для однопролетных зданий; l0=2Н в свободно стоящих стенах и столбах.
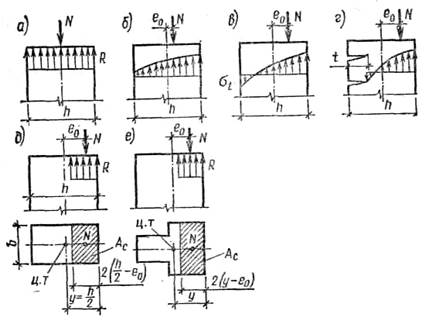
Рис. 17.1. К расчету элемента на центральное и внецентренное сжатие
Значение коэффициентов φ и mg для стен и столбов, опирающихся на неподвижные шарнирные опоры, при расчете сечений, расположенных в средней трети высоты l0, принимают постоянными и равными их значениям, определенным для данного элемента. При расчете сечений на участках в крайних третях l0 коэффициенты φ и mg увеличиваются по линейному закону до единицы на опоре. При других условиях защемления концов элемента φ и mg определяют согласно [5].
Подбор сечений сжатых элементов производят путем последовательных приближений. Задавшись маркой и видом камня и раствора, находят по нормам расчетные сопротивления кладки сжатию. Приняв mg = 1 и φ=0,9, по формуле (17.1) вычисляют размеры столба или стены. По найденным размерам определяют гибкость элемента, уточняют по [5] значения mg и φ и производят повторный расчет.
■ Расчет прочности внецентренно сжатых элементов.
На внецентренное сжатие работают конструкции каменных зданий, в которых продольная сжимающая сила N приложена с эксцентриситетом. Если в сечении одновременно действует центрально-приложенная сила N и изгибающий момент М, то, как уже отмечалось (см. гл. 5), это эквивалентно одной силе N, приложенной с эксцентриситетом относительно центра тяжести сечения е0 = M/N. Характер напряженного состояния каменной кладки в основном зависит от величины эксцентриситета продольной силы е0.
При небольших эксцентриситетах все сечение сжато, эпюра напряжений имеет криволинейное очертание (рис. 17.1, б). По мере увеличения эксцентриситета сжимающие напряжения со стороны, удаленной от силы, уменьшаются, а затем меняют знак, т. е. возникает растяжение (рис. 17.1, в). Когда растягивающие напряжения превысят прочность шва на растяжение, образуется трещина, распространяющаяся на некоторую глубину t (рис. 17.1, г). После образования трещины продолжает работать под нагрузкой только часть сечения высотой h—t. Эксцентриситет приложения продольной силы N для этой части сечения оказывается уменьшенным (на величину t/2), т. е. сечение работает в условиях, приближающихся к центральному сжатию. Поскольку сжимающие напряжения распределены по сечению неравномерно, временное сопротивление кладки сжатию достигается первоначально в краевых участках. Однако при этом несущая способность не исчерпывается, так как в наиболее нагруженных участках вследствие ползучести развиваются значительные деформации, и тогда включаются в работу менее загруженные участки, которые сдерживают поперечные деформации сжатой зоны и тем самым повышают ее временное сопротивление по сравнению с временным сопротивлением при центральном сжатии. Это явление учитывается при расчете коэффициентом со, величина которого для кирпичной кладки прямоугольного сечения находится из выражения ω = 1+е0/h≤1,45; при е0=0 (центральное сжатие) ω=1.
Вследствие сложности напряженного состояния внецентренно сжатых элементов при расчете их прочности исходят из эмпирических формул, основанных на следующих допущениях: растянутая зона, если она имеется, исключается из работы; напряжения в сжатой зоне считаются распределенными равномерно (рис. 17.1, д); неравномерность распределения напряжений по сечению учитывается коэффициентом ω≥l.
Согласно нормам расчет внецентренно сжатых элементов производится по формуле
где mg — коэффициент, учитывающий снижение несущей способности элемента при длительном действии нагрузки вследствие ползучести; φ1 — коэффициент продольного изгиба; Ас — площадь сжатой части сечения при прямоугольной эпюре напряжений (рис. 17.1, д).
Коэффициент
где η — коэффициент, принимаемый по нормам в зависимости от гибкости элемента и вида кладки; для кладки из керамического кирпича при λ≤10 η = 0; Ng — расчетная продольная сила от длительных нагрузок; eog — эксцентриситет от действия длительных нагрузок.
Коэффициент продольного изгиба φ1 определяют как среднее арифметическое между коэффициентом продольного изгиба φ для всего сечения высотой h и коэффициентом продольного изгиба для сжатой части сечения элемента, высота которой для прямоугольного сечения hc = h—2е0. При расчете несущих и самонесущих стен толщиной 25 см и менее следует учитывать случайный эксцентриситет ev, который должен суммироваться с эксцентриситетом продольной силы. Величину случайного эксцентриситета следует принимать: для несущих стен 2 см, для самонесущих 1 см.
Площадь сжатой части сечения Ас определяют из условия, что ее центр тяжести совпадает с точкой приложения расчетной продольной силы N.
В этом случае для прямоугольного сечения размер сжатой зоны будет hc = 2 (h/2 — е0), тогда Ас = hcb = 2 (h/2—e0)b=A(l—2e0/h); при е0=0 Аc=А.
Опыты показывают, что в элементах таврового сечения при эксцентриситетах е0≤0,7y (рис. 17.1, е) (или прямоугольного сечения при е0≤0,35h) может быть допущено небольшое раскрытие трещин в горизонтальных швах. Такое раскрытие не вызывает появления видимых трещин в облицовке и штукатурке стен. Однако при е0>0,7у раскрытие швов становится заметным. Через образовавшиеся трещины в стену может проникать влага, вызывающая ее разрушение. В этом случае помимо расчета прочности необходим расчет кладки по раскрытию трещин.
Следует отметить, что во внецентренно сжатых конструкциях без продольного армирования в растянутой зоне наибольшая величина эксцентриситета (с учетом случайного) не должна превышать для основных сочетаний нагрузок 0,9у, для особых сочетаний — 0,95у, а при стенах толщиной 25 см и менее соответственно 0,8у и 0,85у. При этом расстояние от линии действия силы до более сжатого края сечения для несущих стен и столбов должно быть не менее 2 см.
■ Расчет на местное сжатие (смятие). Местное сжатие или смятие возникает в кладке при действии нагрузки на ограниченную область, т. е. только на часть сечения (рис. 17.2). В этом случае ненагруженная или менее нагруженная часть оказывает сопротивление поперечным деформациям, что приводит к повышению предела прочности кладки, подвергнутой местному сжатию.
Несущая способность сечения при местном сжатии
Nc≤ψdRcAc, (17.4)
где Nc — величина местной нагрузки; ψ — коэффициент полноты эпюры давления от местной нагрузки: при равномерном распределении ψ=1, при треугольной эпюре давления ψ=0,5; d — коэффициент, учитывающий пластическую работу материала, для кирпичной и виброкирпичной кладки d = 1,5—0,5ψ; Rc = ξR — расчетное сопротивление кладки при местном смятии; Ас — площадь смятия, на которую непосредственно передается нагрузка.
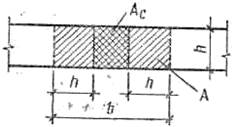
Рис. 17.2. К определению расчетных площадей при местном смятии
Расчетное сопротивление кладки при местном смятии
Rc = ξR,
где ξ= ≤ξ1; R — расчетное сопротивление кладки сжатию; А — расчетная площадь сечения кладки, включая площадь смятия и площадь соседних участков, установленную нормами [5]; ξ1 — коэффициент, учитывающий максимально допустимое увеличение Rc по отношению к R; в зависимости от вида кладки и схемы расположения площади смятия ξ1 = 1…2.
Если под опорами изгибаемых элементов не требуется установка распределительных плит, то для кладок из кирпича и бетонных камней допускается принимать ψd=1.
■ Расчет прочности изгибаемых элементов. Проектирование неармированных конструкций, работающих на изгиб, допускается только для кладок, работающих по перевязанному сечению. К таким конструкциям относятся подпорные стенки с вертикальными контрфорсами, стены здания между колоннами и т. п. Расчет сечений производят на действие изгибающего момента М и поперечной силы Q. При этом кладку условно рассматривают как упругий материал. Тогда по аналогии с известными положениями сопротивления материалов расчетные формулы примут вид:
■ при действии изгибающего момента
где Rtb — расчетное сопротивление кладки растяжению по перевязанному шву; W — момент сопротивления кладки при упругой ее работе;
●при действии поперечной силы
где Rtw — расчетное сопротивление кладки главным растягивающим напряжениям при изгибе, численно равное Rtb; b — ширина сечения; z — плечо внутренней пары, для прямоугольного сечения z=2h/3.
■ Расчет по образованию и раскрытию трещин. Расчет внецентренно сжатых неармированных элементов при е0>0,7у помимо прочности производят по образованию и раскрытию трещин.
При расчете по раскрытию трещин (швов кладки) определяют краевые напряжения в сечении по неперевязанному шву в предположении упругой работы кладки, которые в целях ограничения ширины раскрытия трещин не должны превышать расчетного сопротивления кладки по неперевязанному сечению Rtb, умноженному на коэффициент условий работы γr:
где N — расчетная продольная сила; W — момент сопротивления сечения.
Коэффициент γr зависит от предполагаемого срока службы конструкции, характеристики и условий работы кладки. Так, для неармированной кладки внецентренно нагруженных конструкций при сроке их службы до 50 лет γr=2, а для конструкций при том же сроке службы, но испытывающих гидростатическое давление жидкости и снабженных гидроизоляцией, γr =1,5.
Полагая, что в выражении (17.7) M=Ne0, и производя преобразования, получают
где I—момент инерции сечения; (h—у) — расстояние от центра тяжести сечения до наиболее удаленной растянутой грани.
Конструкции, в которых по условию эксплуатации не может быть допущено появление трещин в штукатурных и других покрытиях, должны быть проверены по допустимым деформациям растянутых поверхностей. Эти деформации для неармированной кладки следует определять при нормативных нагрузках, которые будут приложены после нанесения штукатурки или других покрытий. Расчет по деформациям растянутых поверхностей каменных конструкций из неармированной кладки производится по формулам:
●при осевом растяжении
●при внецентренном сжатии
где Е — модуль деформаций кладки Е=0,8Е0; еu — предельная деформация кладки, при которой еще не происходит появление трещин; назначается в зависимости от вида штукатурки.
Источник
