Расчет элементов цельного сечения на центральное растяжение
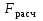
Элементами
деревянных конструкций называют доски,
бруски, брусья и бревна цельного сечения
с размерами, указанными в сортаментах
пилёных и круглых материалов. Они могут
являться самостоятельными конструкциями,
например, балками или стойками, а также
стержнями более сложных конструкций.
Усилия в элементах определяют общими
методами строительной механики. Проверка
прочности и прогибов элемента заключается
в определении напряжений в сечениях,
которые не должны превышать расчетных
сопротивлений древесины, а также его
прогибов, которые не должны превосходить
предельных, установленных нормами
проектирования. Деревянные элементы
рассчитывают в соответствии со СНиП
II-25-80.
Растянутые
элементы
Н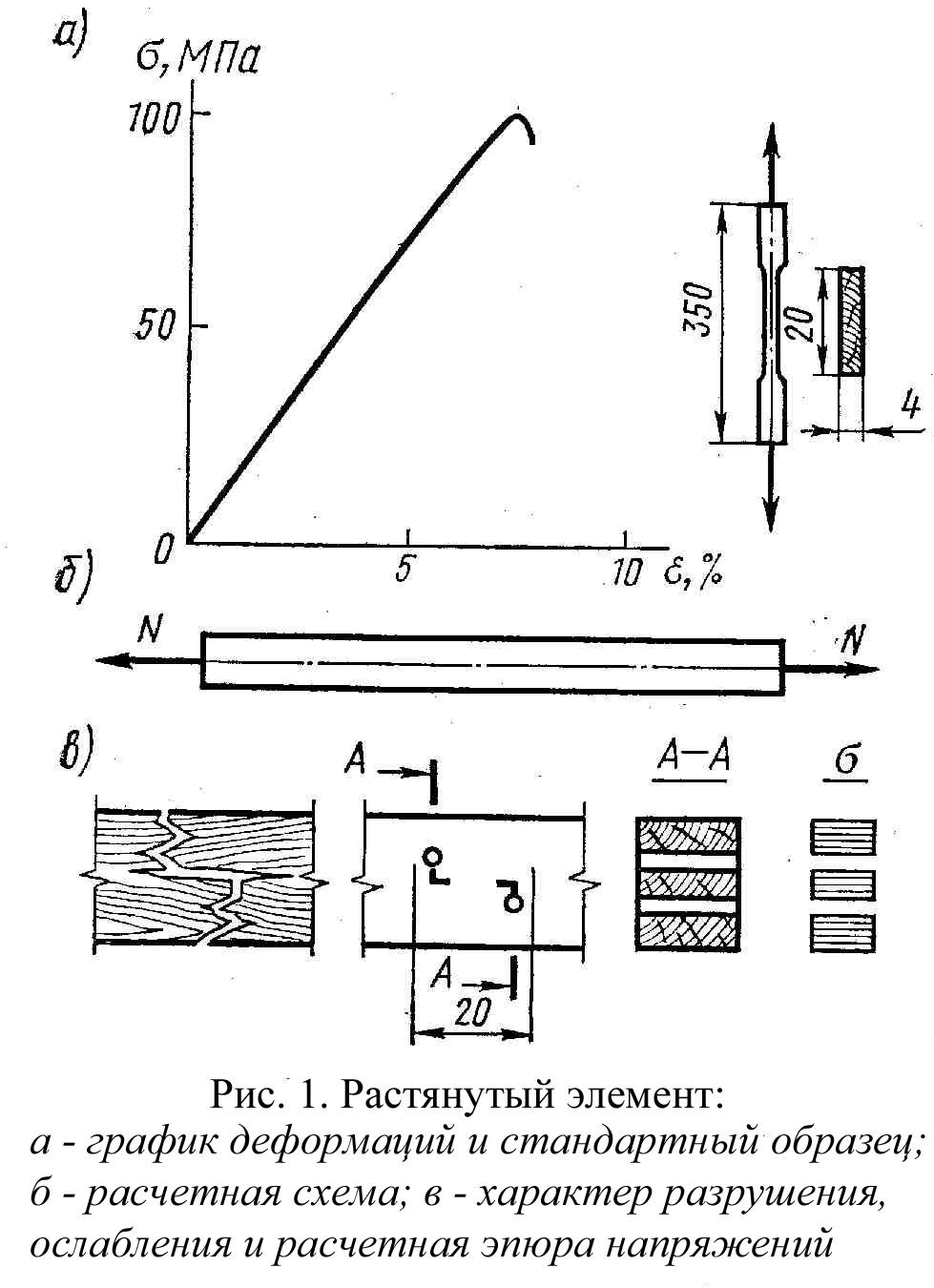 а
а
растяжение работают нижние пояса и
отдельные раскосы ферм, затяжки арок и
других сквозных конструкций. Растягивающее
усилиеN
действует вдоль оси элемента и во всех
точках его поперечного сечения возникают
растягивающие напряжения σ,
которые с достаточной точностью считаются
одинаковыми по величине.
Древесина на
растяжение работает почти упруго и
показывает высокую прочность. Разрушение
происходит хрупко в виде почти мгновенного
разрыва. Стандартные образцы при
испытаниях на растяжение имеют вид
«восьмерки».
Как видно из
диаграммы растяжения древесины без
пороков, зависимость деформаций от
напряжений близка к линейной, а прочность
достигает 100 МПа.
Однако прочность
реальной древесины при растяжении,
учитывая ее значительные колебания,
большое влияние пороков и длительности
нагружения значительно ниже: для
неклееной древесины I
сорта Rр=10
МПа, для клееной древесины влияние
пороков уменьшается, поэтому Rр=12
МПа. Прочность растянутых элементов в
тех местах, где есть ослабления снижается
в результате концентрации напряжений
у их краев, т.е. вводится коэффициент
условия работы m=0,8.
Тогда получается расчетное сопротивление
Rр=8
МПа. Проверочный расчет растянутых
элементов производится по формуле:
σ,
где
–площадь
рассматриваемого поперечного сечения,
причем ослабления, расположенные на
участке длиной 20 см. считаются совмещенными
в одном сечении. Для подбора сечений
пользуются этой же формулой, но
относительно искомой (требуемой) площади
.
Сжатые элементы
Н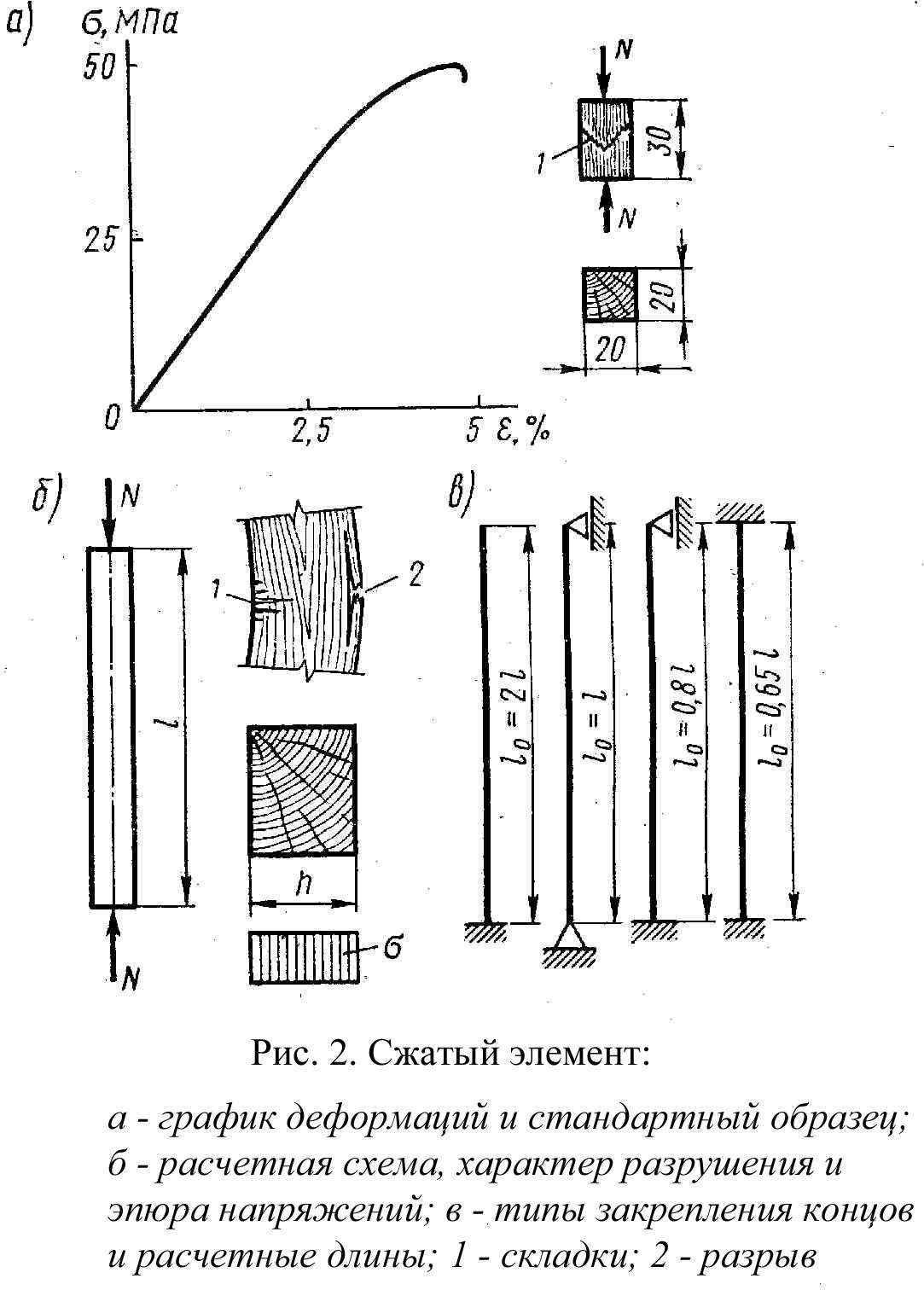 а
а
сжатие работают стойки, подкосы, верхние
пояса и отдельные стержни ферм. В сечениях
элемента от сжимающего усилияN,
действующего
вдоль его оси, возникают почти одинаковые
по величине сжимающие напряжения σ(эпюра
прямоуголная).
Стандартные образцы
при испытании на сжатие имеют вид
прямоугольной призмы с размерами,
указанными на рис. 2.
Древесина работает
на сжатие надежно, но не вполне упруго.
Примерно до половины предела прочности
рост деформаций происходит по закону
близкому к линейному, и древесина
работает почти упруго. При росте нагрузки
увеличение деформаций все более опережает
рост напряжений, указывая на
упруго-пластический характер работы
древесины.
Разрушение образцов
без пороков происходит при напряжениях,
достигающих 44 МПа, пластично, в результате
потери устойчивости ряда волокон, о чем
свидетельствует характерная складка.
Пороки меньше снижают прочность
древесины, чем при растяжении, поэтому
расчетное сопротивление реальной
древесины при сжатии выше и составляет
для древесины 1 сорта Rс=14÷16
МПа, а для 2 и 3 сортов эта величина немного
ниже.
Расчет на прочность
сжатых элементов производится по
формуле:
σ,
где
Rс
– расчетное сопротивление сжатию.
Аналогичным образом
рассчитываются и сминаемые по всей
поверхности элементы. Сжатые стержни,
имеющие большую длину и не закрепленные
в поперечном направлении должны быть,
помимо расчета на прочность, рассчитаны
на продольный изгиб. Явление продольного
изгиба заключается в том, что гибкий
центрально-сжатый прямой стержень
теряет свою прямолинейную форму (теряет
устойчивость) и начинает выпучиваться
при напряжениях, значительно меньших
предела прочности. Проверку сжатого
элемента с учетом его устойчивости
производят по формуле:
σ,
где
–расчетная площадь
поперечного сечения,
φ – коэффициент
продольного изгиба.
принимается равной:
1. При отсутствии
ослаблений =,
2. При ослаблениях,
не выходящих на кромки, если площадь
ослаблений не превышает 25% ,
=,
3. То же, если площадь
ослаблений превышает 20% ,
=4/3,
При симметричных
ослаблениях, выходящих на кромки =,
При несимметричном
ослаблении, выходящем на кромки, элементы
рассчитывают как внецентренно сжатые.
Коэффициент
продольного изгиба φ
всегда меньше
1, учитывает влияние устойчивости на
снижение несущей способности сжатого
элемента в зависимости от его расчетной
максимальной гибкости λ.
Гибкость элемента
равна отношению расчетной длины lк радиусу
инерции сечения элемента:
;
.
Расчетную длину
элемента lследует
определять умножением его свободной
длины l
на коэффициент μ:
l=l
μ,
где
коэффициент μпринимается
в зависимости от типа закрепления концов
элемента:
— при шарнирно
закрепленных концах μ=1;
— при одном шарнирно
закрепленном, а другом защемленном
μ=0,8;
— при одном
защемленном, а другом свободном
нагруженном конце μ=2,2;
— при обоих
защемленных концах μ=0,65.
Гибкость сжатых
элементов ограничивается с тем, чтобы
они не получились недопустимо гибкими
и недостаточно надежными. Отдельные
элементы конструкций (отдельные стойки,
пояса, опорные раскосы ферм и т.п.) должны
иметь гибкость не более 120. Прочие сжатые
элементы основных конструкций – не
более 150, элементы связей – 200.
При гибкости
более 70 (λ>70)
сжатый элемент теряет устойчивость,
когда напряжения сжатия в древесине
еще невелики и она работает упруго.
Коэффициент
продольного изгиба (или коэффициент
устойчивости), равный отношению напряжения
в момент потери устойчивости σкрк пределу
прочности при сжатии Rпр,
определяют по формуле Эйлера с учетом
постоянного отношения модуля упругости
древесины к пределу прочности:
,
где
А=3000
– для древесины,
А=2500
– для фанеры.
При гибкостях,
равных и меньших 70 (λ≤70)
элемент теряет устойчивость, когда
напряжения сжатия достигают
упругопластической стадии и модуль
упругости древесины понижается.
Коэффициент продольного изгиба при
этом определяют с учетом переменного
модуля упругости по упрощенной
теоретической формуле:
,
где
=0,8
– коэффициент для древесины;
=1
– коэффициент для фанеры.
При подборе сечения
используют формулу расчета на устойчивость,
предварительно задаваясь величиной λ
и φ.
Изгибаемые
элементы
В изгибаемых
элементах от нагрузок, действующих
поперек продольной оси, возникают
изгибающие моменты М
и поперечные силы Q,
определяемые методами строительной
механики. Например, в однопролетной
балке пролетом l
от равномерно-распределенной нагрузки
q
возникают изгибающие моменты
и поперечные силы .
От изгибающего
момента в сечениях элемента возникают
деформации и напряжения изгиба σ,
которые состоят из сжатия в одной части
сечения и растяжения в другой, в результате
элемент изгибается.
Диаграмма как и
для сжатия, примерно до половины, имеет
линейное очертание, затем изгибается,
показывая ускоренный рост прогибов.
=80
МПа – предел прочности чистой древесины
на изгиб при кратковременных испытаниях.
Разрушение образца начинается с появления
складок в крайних сжатых волокнах и
завершается разрывом крайних растянутых.
Расчетное сопротивление изгибу по СНиП
II-25-80
рекомендуется принимать таким же, как
и при сжатии, т.е. для 1 сорта Rи=14
МПа – для элементов прямоугольного
сечения высотой до 50 см. Брусья с размерами
сечения 11 – 13 см. при высоте сечения 11
– 50 см. имеют меньше перерезанных волокон
при распиловке, чем доски, поэтому их
прочность повышается до Rи=15
МПа. Бревна шириной свыше13 см. при высоте
сечения 13 – 50 см. совсем не имеют
перерезанных волокон, поэтому Rи=16
МПа.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
2.2.1. Расскажите о предельном состоянии, и расчете центрально-растянутого деревянного элемента. Приведите примеры использования таких стержней в конструкциях зданий и сооружений
Центрально-растянутым (рис. 2.1) считается элемент, испытывающий действие растягивающей силы, создающей нормальные напряжения, равномерно распределенные по всему его поперечному сечению (не имеющему, ослаблений или ослабленному). Древесина работает на растяжение почти как упругий
Рис. 2.1 Центрально-растянутый элемент: а – не имеющий ослаблений; б – с ослаблениями в расчетном сечении
материал и имеет достаточно высокую прочность. Для растянутых деревянных элементов характерно почти мгновенное разрушение от разрыва наименее прочных волокон, который происходит практически без проявления заметных дополнительных деформаций. Поэтому единственным условием при расчете центрально-растянутых стержней является обеспечение прочности, т. е. выполнение условия первой группы предельных состояний.
(2.9)
где N — растягивающая сила от расчетных нагрузок;
Fнт — площадь нетто поперечного сечения стержня;
Rр— расчетное сопротивление древесины растяжению.
Согласно требованию Норм, площадь нетто здесь определяется за вычетом площади всех ослаблений, находящихся на длине 20 см. Причину этого легко понять, если помнить о неоднородностях строения древесины и наличии допустимых пороков в реальных растянутых элементах — разрушение может произойти не точно по поперечному сечению, а уступами или зигзагами именно на такой примерно длине (рис. 2.1б). Это является особенностью расчета деревянного растянутого элемента. Другой особенностью является учет влияния концентрации напряжений в ослабленном сечении путем снижения величины расчетного сопротивления на 20 %, что достигается введением коэффициента условий работы то = 0,8.
В конструкциях центрально-растянутые элементы встречаются в виде нижних поясов или растянутых раскосов деревянных ферм, деревянных подвесок или других подобных стержней.
Учитывая хрупкий характер разрушения и сильное влияние пороков на прочность растянутого элемента, их изготавливают, как правило, из наиболее прочной древесины первого сорта с нормативным сопротивлением Rн=20МПа и расчетным сопротивлением R =10 МПа. При отсутствии такого материала допускается применять древесину второго сорта с R=7,0 МПа. Рекомендуется наиболее ответственные растянутые элементы проектировать площадью не менее 50 см2.
По деформациям растянутые элементы не проверяются. При необходимости подобрать сечение растянутого элемента или определить наибольшее усилие, которое может выдержать растянутый элемент, пользуются формулой (2.9), решенной относительно Fтр или N.
2.2.2. Покажите на примере, как проверить прочность центрально-растянутого деревянного элемента при известных усилиях, размерах поперечного сечения и условиях его эксплуатации
Исходные данные: расчетное усилие N = 80кН; материал — лиственница европейская, второго сорта; растянутым элементом является раскос многоугольной металлодаревянной фермы, эксплуатируемой в помещении с t = 18°C при j = 60%; доля постоянных и временных длительных нагрузок, действующих на покрытие, составляет 70% от суммарной; коэффициент надежности по назначению gn = 0,95; расчетная схема и сечение раскоса приведены на рис. 2.2.
Рис. 2.2. Центрально-растянутый элемент, ослабленный отверстиями под болты
Решение
Определяются класс условий эксплуатации (в дальнейшем КУЭ) конструкции по табл. 1 [1]. Согласно задания – КУЭ – 1, подкласс – 1.2.
Определяется величина расчетного сопротивления древесины европейской лиственницы второго сорта на растяжение вдоль волокна с учетом коэффициентов условий работы. Согласно табл. 3 и п. 5.2 [1]
Определяется площадь нетто расчетного сечения раскоса. Поскольку отверстия расположены на расстоянии более 200 мм друг от друга, учитывается ослабление одним отверстием:
Проверяется прочность раскоса в ослабленном отверстием сечении с учетом назначения конструкций (здесь gn введен в усилия)
Вывод: Прочность раскоса обеспечена.
2.2.3. Расскажите о предельных состояниях центрально-сжатых деревянных элементов. Приведите примеры использования таких стержней в конструкциях. Что такое «короткий» и «длинный» стержень? На что и как это влияет?
На центральное сжатие могут работать деревянные колонны, стойки, подкосы, верхние пояса и отдельные стержни ферм. В сечениях сжатого стержня возникают нормальные напряжения, равномерно распределенные по всему поперечному сечению (рис. 2.3б). Сжатые деревянные стержни работают более надежно, чем растянутые, и разрушаются только после заметных деформаций. Это результат потери местной устойчивости стенок наиболее слабых клеток, выражается образованием характерной складки на поверхности элемента (рис. 2.3 в).
Рис. 2.3. Центрально-сжатые элементы: а–возможные варианты стержней и их ослаблений; б –характер разрушения от потери устойчивости сжатых и разрыва растянутых волокон: 1-без ослаблений; 2- площадь ослабления более 25% от всего сечения; 3- ослабления вышли на кромки сечения; 4- ослабление площадью менее 25% от всего сечения
Однако такой характер разрушения наблюдается лишь в случае, когда нормальные напряжения в стержне превышают величину, соответствующую пределу упругой работы древесины, и переходят в область упругопластической работы древесины. Это возможно только тогда, когда гибкость работающего стержня очень мала. При значительных гибкостях деревянные стержни разрушаются задолго до того, когда напряжения в них достигнут предела прочности (или расчетного сопротивления). Это происходит из-за общей потери устойчивости стержней. Поэтому деревянные сжатые стержни принято делить на «короткие» — длиной менее 7 наименьших размеров попе
речного сечения, и «длинные» — большей длины. Первые достаточно проверить лишь на прочность, а вторые требуют проверки как на прочность, так и на устойчивость.
Проверка на прочность осуществляется по формуле
(2.10) Проверка на устойчивость имеет вид . (2.11)
Здесь — коэффициент продольного изгиба; — расчетная площадь поперечного сечения, принимаемая равной либо Fбр, если ослаблений нет или их меньше 25% Fбр, либо 4/3 Fнт, если ослаблений более 25% Fбр, либо Fнт, если ослабления выходят на кромки симметрично.
Источник
На сжатие работают стойки, подкосы, верхние пояса и отдельные стержни ферм и др. сквозные конструкции. Древесина работает на сжатие более надёжно, чем на растяжение, но не вполне упруго. Здесь пластические свойства древесины проявляются значительно сильнее, чем при растяжении. В данном случае пороки реальной древесины меньше снижают прочность сжатых элементов, поскольку сами воспринимают часть сжимающих напряжений. В растянутых элементах пороки выключаются из работы моментально. Вследствие, этого сжатые элементы рекомендуется изготавливать, как правило, из более доступной древесины 2 сорта.
Расчёт центрально сжатых элементов на прочность следует производить по формуле: δс=N/Fнт≤Rс,
В основном расчёт на прочность необходим для коротких стержней, у которых длина ≤ 7 толщин. Более длинные элементы, не закреплённые в поперечном направлении связями следует рассчитывать продольный изгиб, который состоит в потере гибким центрально сжатым прямым стержнем своей прямолинейной формы, что называется потерей устойчивости. Потеря устойчивости происходит раньше, чем напряжение сжатия достигнет придела прочности. При потере устойчивости несущий элемент теряет несущую способность и выгибается в сторону. При дальнейшем выгибе на вогнутой стороне появляются складки, свидетельствующие о разрушении от сжатия, а их выпуклая разрушается от растяжения.
На устойчивость ведут расчёт по формуле: δс=N/(φ×Fрасч)≤Rс, δс=N/ Fрасч≤ φ×Rс,
Прочность стержня при сжатии и потери устойчивости зависят от площади Fрасч и формы его сечения, длины l и также закрепления концов стержня, что учитывается коэффициентом устойчивости или коэффициентом продольного изгиба (φ),
А) ослабление не выходит на кромку, т.е. располагаются в середине сечения. При отсутствии ослаблений или ослаблений в опасных сечениях не выходящих на кромку, если площадь ослабления не превышает 25% полного сечения Fбр, то Fрасч = Fбр,
Б)При ослаблении не выходящих на кромки, если площадь ослабления превышает 25% Fбр, то:
Fрасч = 4/3×Fнт ,
В) Симметричное ослабления, выходящие на кромки, то: Fрасч = Fнт .
Коэффициент продольного изгиба (φ)элемента определяется в зависимости от его расчётной длины l0, радиуса инерции r,таким образом зависит от гибкости элементов: λ= l0/r;
В общем случае коэф. продольного изгиба можно найти следующим образом: φ=δкр/Rврс;
Т.е устойчивость определяется критическим напряжением δкр.
δкр=Nкр/F , теоретическое значение критической нагрузки для абсолютно упругого стержня было определено Эйлером: Nкр =Π×Е×У/ l20 ;
l0- расчётная длина, которая учитывает влияние типа закрепления концов стержня на устойчивость.
Вообще критическая сила – это максимальная сила способная удержать стержень в искривлённом состоянии при котором может быть раздвоение оси стержня (1 критическая сила).
; ; следовательно , при λ>70.
то для древесины будет равно А=3000, для фанеры А=2500,
при λ>70
Формула Эйлера справедлива только в тех случаях, когда стержень теряет устойчивость при напряжении ≤ пределу пропорциональности, когда модуль упругости постоянен. Е=const и придел материала так же постоянен.
Если построить кривую Эйлера, то будет видно, что при малых гибкостях, когда критическое напряжение превышает предел пропорциональности, коэффициент продольного изгиба получается больше 1, чего по существу быть не может. Поэтому
при λ≤70 то
Эта формула получена опытным путём, соответствует работе стержня за пределом пропорциональности, когда меняется модуль упругости (Е≠const), а=0,8 – для древесины, а=1 – для фанеры.
Если l0/h≤7, то φ≈1,
Гибкость зависит от радиуса инерции сечения ; , для прямоугольного сечения
для круглого сечения ;
Гибкость λ сжатых элементов ограничивается с тем, чтобы они получились недопустимо неустойчивыми и недостаточно надёжными. Поэтому гибкость элемента ограничивают, например:
-отдельные стойки, верхние пояса ферм, опорные раскосы ферм λ≤[λ]=120
-прочие сжатые элементы основных несущих конструкций λ≤150
-сжатые элементы связей λ≤200
Источник
Как уже отмечалось, на работу древесины при растяжении существенно влияет наличие естественных пороков древесины (сучки, косослой и др.), поэтому для растянутых элементов рекомендуется применять древесину 1-го и 2-го сортов.
Расчет прочности центрально-растянутых деревянных элементов выполняется по формуле (5.1, в) (здесь и далее в расчетах центрально-растянутых деревянных элементов сохранены обозначения, принятые в СНиП 11-25-80):
где N — расчетная продольная сила; Fm — площадь поперечного сечения элемента нетто; Rp — расчетное сопротивление древесины растяжению вдоль волокон (принимается с коэффициентами условия работы тг значения которых определяются в соответствии с указаниями п. 3.2 СНиП И-25-80; так, при наличии ослаблений в расчетном сечении растянутых элементов следует учитывать коэффициент условия работы т0 = 0,8).
При определении площади нетто в растянутых деревянных конструкциях принимается во внимание, что при их разрушении линия разрыва может проходить через ослабления, расположенные не в одной плоскости. Поэтому ослабления, расположенные на длине 200 мм, суммируются (рис. 6.2).
Рис. 6.2. К определению площади нетто:
FHT — площадь сечения элемента нетто; Рослабл — площадь ослаблений
Нормы ограничивают гибкость центрально-растянутых деревянных элементов и отдельных ветвей. Предельные гибкости принимаются в соответствии с табл. 14СНиП П-25-80. Так, например, для растянутых элементов ферм в вертикальной плоскости предельная гибкость А,тах = 150, для прочих растянутых элементов ферм и других сквозных конструкций А,тах = 200.
Проверка гибкости выполняется по формуле (5.3, в):
где /0 — расчетная длина элемента; г — радиус инерции сечения; ^шах — предельная гибкость.
Порядок расчета центрально-растянутого деревянного элемента (тип 1)
- 1. Принимают древесину и ее сорт; определяют расчетное сопротивление растяжению вдоль волокон (для древесины сосны, ели) Rp (табл. 2.4); в случае если элемент выполнен из древесины других пород, расчетное сопротивление умножают на переходной коэффициент тп (табл. 2.5).
- 2. Определяют коэффициенты условия работы в соответствии с указаниями п. 3.2 СНиП И-25-80 (так, при наличии отверстий, врезок следует учитывать коэффициент условия работы т0 = 0,8).
- 3. Определяют требуемую площадь сечения нетто FTTpe6:
- • если элемент не имеет ослаблений (отверстий, врезок), площади сечения брутто и нетто равны, F- Fm;
- • если в элементе имеются ослабления, необходимо требуемую площадь сечения определять как сумму требуемой площади нетто и площади ослабления (величину ослабления назначают, предварительно задавшись толщиной элемента, впоследствии возможна корректировка принятых размеров).
- 4. По требуемой площади подбирают сечение элемента и определяют фактические значения площадей брутто, нетто, значения радиусов инерции сечения.
- 5. Выполняют проверку подобранного сечения:
- • проверяют гибкость: X = — ?1макс;
г
N
• проверяют прочность: о = — ILm .
F у
1 нт
Задача 2-го типа — проверка прочности центрально-растянутого элемента является частью задачи 1-го типа (выполнение п. 5 порядка расчета).
Примеры расчета центрально-растянутых элементов
Пример 6.1. Подобрать сечение стальной подвески, выполненной из листовой стали (рис. 6.3). Подвеска центрально-растянута силой N= 200 кН; уп= 1,0.
Решение
1. Принимаем сталь С 245; устанавливаем расчетное сопротивление стали по пределу текучести Ry = 240 МПа = 24 кН/см2 (табл. 2.2).
Рис. 6.3. К примеру 6.1
- 2. Устанавливаем величину коэффициента условия работы: ус = = 0,9 (табл. 2.3).
- 3. Определяем требуемую площадь сечения нетто Ап:
4. Принимаем толщину листа, из которого выполняется подвеска, и определяем площадь ослабления:
5. Определяем требуемую площадь сечения с учетом площади, занятой ослаблением:
6. Определяем требуемую ширину подвески и назначаем ее сечение:
принимаем сечение подвески 8 х 160 мм.
7. Проверяем прочность; для этого предварительно определяем фактическое значение площади сечения нетто:
прочность сечения обеспечена; нормами гибкость подвески не ограничивается (см. табл. 20 СНиП 11-23-81*).
Вывод. Принимаем сечение подвески 8 х 160 мм из стали С245.
Рис. Б.4. К примеру 6.2. Крепление затяжки к поясу фермы
Пример 6.2. Проверить прочность и гибкость центрально-растянутой деревянной затяжки треугольной безраскосной фермы, выполненной из доски сечением 50 х 125 мм, которая прикреплена к верхнему поясу стропильной фермы болтом d = 12 мм и четырьмя гвоздями d= 5 мм, /=150 мм (рис. 6.4). Древесина — сосна, сорт 1. Усилие в затяжке N= 34,0 кН; уп = 0,95. Расчетная длина /0 = 2,5 м. Условия эксплуатации фермы Б2.
Решение
1. Находим усилие в затяжке с учетом коэффициента надежности по ответственности уп:
2. Определяем расчетное сопротивление древесины растяжению вдоль волокон:
3. Определяем коэффициенты условий работы:
4. Находим площадь сечения нетто:
5. Проверяем прочность затяжки:
прочность обеспечена.
6. Определяем радиусы инерции затяжки (табл. 5.2):
/
7. В соответствии с табл. 14 СНиП П-25-80 для прочих растянутых элементов ферм (к которым относится затяжка) предельная гибкость А,тах = 200. Проверяем гибкость затяжки:
Вывод. Прочность и гибкость затяжки отвечают требованиям норм.
Задачи для самостоятельной работы
Задача 6.1. Проверить прочность и гибкость стального центрально-растянутого стержня круглого сечения (рис. 6.5). Растягивающая сила N= 30 кН, уп = 0,9. Сталь С345; ус = 0,95. Расчетная длина стержня lef = 1000 мм. Предельная гибкость А,пред = 400.
Рис. 6.5. К задаче 6.1
Задача 6.2. Подобрать сечение центрально-растянутого нижнего пояса деревянной фермы. Материал: брус, сосна, сорт 2. Условия эксплуатации Б2 (тв = 1,0). В нижнем поясе имеется ослабление за счет врезки (т0 = 0,8) глубиной Авр = 4 см (рис. 6.6). На нижний пояс действует растягивающая сила 7V= 200 кН; уп = 0,95. Расчетная длина /0 = 3,0 м. СНиП Н-25-80 ограничивает предельную гибкость растянутых поясов в вертикальной плоскости А,тах = 150.
Рис. 6.6. К задаче 6.2
Источник
