Расчет фермы на растяжение

Фермами называют плоские и пространственные стержневые конструкции с шарнирными соединениями элементов, загружаемые исключительно в узлах. Шарнир допускает вращение, поэтому считается, что стержни под нагрузкой работают только на центральное растяжение-сжатие. Фермы позволяют значительно сэкономить материал при перекрытии больших пролётов.

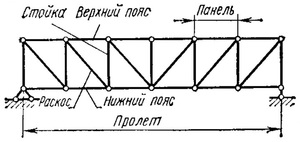
Рисунок 1

Фермы классифицируются:

• по очертанию внешнего контура;
• по виду решётки;
• по способу опирания;
• по назначению;
• по уровню проезда транспорта.

Также выделяют простейшие и сложные фермы. Простейшими называют фермы, образованные последовательным присоединением шарнирного треугольника. Такие конструкции отличаются геометрической неизменяемостью, статической определимостью. Фермы со сложной структурой, как правило, статически неопределимы.

Для успешного расчёта необходимо знать виды связей и уметь определять реакции опор. Эти задачи подробно рассматриваются в курсе теоретической механики. Разницу между нагрузкой и внутренним усилием, а также первичные навыки определения последних дают в курсе сопротивления материалов.

Рассмотрим основные методы расчёта статически определимых плоских ферм.

Способ проекций

На рис. 2 симметричная шарнирно-опёртая раскосная ферма пролётом L = 30 м, состоящая из шести панелей 5 на 5 метров. К верхнему поясу приложены единичные нагрузки P = 10 кН. Определим продольные усилия в стержнях фермы. Собственным весом элементов пренебрегаем.

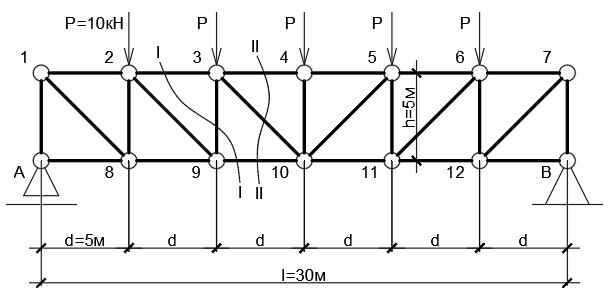
Рисунок 2

Опорные реакции определяются путём приведения фермы к балке на двух шарнирных опорах. Величина реакций составит R (A) = R (B) = ∑P/2 = 25 кН. Строим балочную эпюру моментов, а на её основе — балочную эпюру поперечных усилий (она понадобится для проверки). За положительное направление принимаем то, что будет закручивать среднюю линию балки по часовой стрелке.

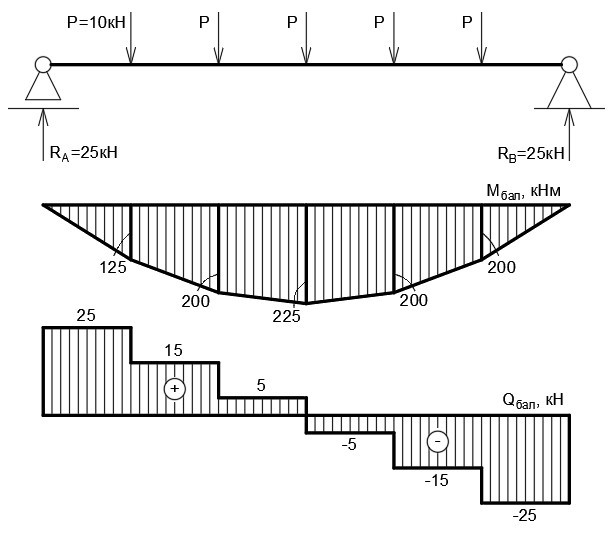
Рисунок 3

Метод вырезания узла

Метод вырезания узла заключается в отсечении отдельно взятого узла конструкции с обязательной заменой разрезаемых стержней внутренними усилиями с последующим составлением уравнений равновесия. Суммы проекций сил на оси координат должны равняться нулю. Прикладываемые усилия изначально предполагаются растягивающими, то есть направленными от узла. Истинное направление внутренних усилий определится в ходе расчёта и обозначится его знаком.

Рационально начинать с узла, в котором сходится не более двух стержней. Составим уравнения равновесия для опоры, А (рис. 4).

∑ F (y) = 0: R (A) + N (A-1) = 0

∑ F (x) = 0: N (A-8) = 0

Очевидно, что N (A-1) = -25кН. Знак «минус» означает сжатие, усилие направлено в узел (мы отразим это на финальной эпюре).

Условие равновесия для узла 1:

∑ F (y) = 0: -N (A-1) — N (1−8)∙cos45° = 0

∑ F (x) = 0: N (1−2) + N (1−8)∙sin45° = 0

Из первого выражения получаем N (1−8) = —N (A-1)/cos45° = 25кН/0,707 = 35,4 кН. Значение положительное, раскос испытывает растяжение. N (1−2) = -25 кН, верхний пояс сжимается. По этому принципу можно рассчитать всю конструкцию (рис. 4).

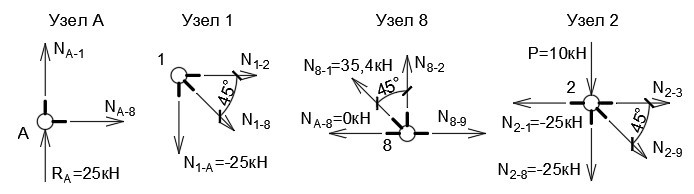
Рисунок 4

Метод сечений

Ферму мысленно разделяют сечением, проходящим как минимум по трём стержням, два из которых параллельны друг другу. Затем рассматривают равновесие одной из частей конструкции. Сечение подбирают таким образом, чтобы сумма проекций сил содержала одну неизвестную величину.

Проведём сечение I-I (рис. 5) и отбросим правую часть. Заменим стержни растягивающими усилиями. Просуммируем силы по осям:

∑ F(y) = 0: R(A) — P + N(9−3)

N(9−3) = P — R(A) = 10 кН — 25 кН = -15 кН

Стойка 9−3 сжимается.

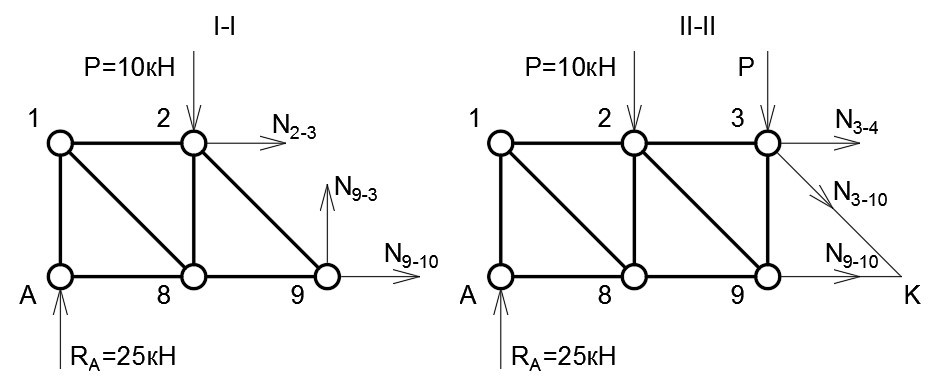
Рисунок 5

Способ проекций удобно применять в расчётах ферм с параллельными поясами, загруженными вертикальной нагрузкой. В этом случае не придётся вычислять углы наклона усилий к ортогональным осям координат. Последовательно вырезая узлы и проводя сечения, мы получим значения усилий во всех частях конструкции. Недостатком способа проекций является то, что ошибочный результат на ранних этапах расчёта повлечёт за собой ошибки во всех дальнейших вычислениях.

Способ моментной точки

Способ моментной точки требует составлять уравнение моментов относительно точки пересечения двух неизвестных сил. Как и в методе сечений, три стержня (один из которых не пересекается с остальными) разрезаются и заменяются растягивающими усилиями.

Рассмотрим сечение II-II (рис. 5). Стержни 3−4 и 3−10 пересекаются в узле 3, стержни 3−10 и 9−10 пересекаются в узле 10 (точка K). Составим уравнения моментов. Суммы моментов относительно точек пересечения будут равняться нулю. Положительным принимаем момент, вращающий конструкцию по часовой стрелке.

∑ m(3) = 0: 2d∙R(A) — d∙P — h∙N(9−10) = 0

∑ m(K) = 0: 3d∙R(A) — 2d∙P — d∙P + h∙N(3−4) = 0

Из уравнений выражаем неизвестные:

N(9−10) = (2d∙R(A) — d∙P)/h = (2∙5м∙25кН — 5м∙10кН)/5м = 40 кН (растяжение)

N(3−4) = (-3d∙R(A) + 2d∙P + d∙P)/h = (-3∙5м∙25кН + 2∙5м∙10кН + 5м∙10кН)/5м = -45 кН (сжатие)

Способ моментной точки позволяет определить внутренние усилия независимо друг от друга, поэтому влияние одного ошибочного результата на качество последующих вычислений исключено. Данным способом можно воспользоваться в расчёте некоторых сложных статически определимых ферм (рис. 6).

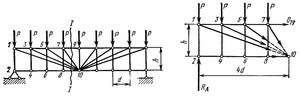
Рисунок 6

Требуется определить усилие в верхнем поясе 7−9. Известны размеры d и h, нагрузка P. Реакции опор R(A) = R(B) = 4,5P. Проведём сечение I-I и просуммируем моменты относительно точки 10. Усилия от раскосов и нижнего пояса не попадут в уравнение равновесия, так как сходятся в точке 10. Так мы избавляемся от пяти из шести неизвестных:

∑ m(10) = 0: 4d∙R(A) — d∙P∙(4+3+2+1) + h∙O(7−9) = 0

O(7−9) = -8d∙P/h

Аналогично можно рассчитать остальные стержни верхнего пояса.

Признаки нулевого стержня

Нулевым называют стержень, в котором усилие равно нулю. Выделяют ряд частных случаев, в которых гарантированно встречается нулевой стержень.

• Равновесие ненагруженного узла, состоящего из двух стержней, возможно только в том случае, если оба стержня нулевые.
• В ненагруженном узле из трёх стержней одиночный (не лежащий на одной прямой с остальными двумя) стержень будет нулевым.

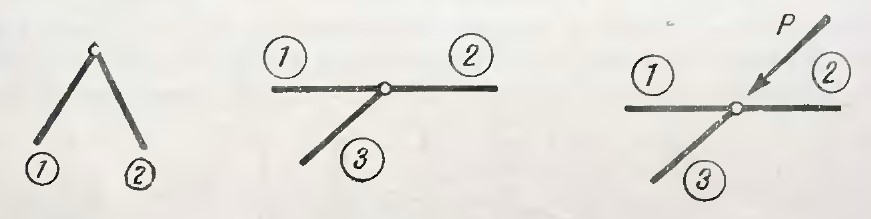
Рисунок 7

• В трехстержневом узле без нагрузки усилие в одиночном стержне будет равно по модулю и обратно по направлению приложенной нагрузке. При этом усилия в стержнях, лежащих на одной прямой, будут равны друг другу, и определятся расчётом N(3) = -P, N(1) = N(2).
• Трехстержневой узел с одиночным стержнем и нагрузкой, приложенной в произвольном направлении. Нагрузка P раскладывается на составляющие P’ и P» по правилу треугольника параллельно осям элементов. Тогда N(1) = N(2) + P’, N(3) = -P».

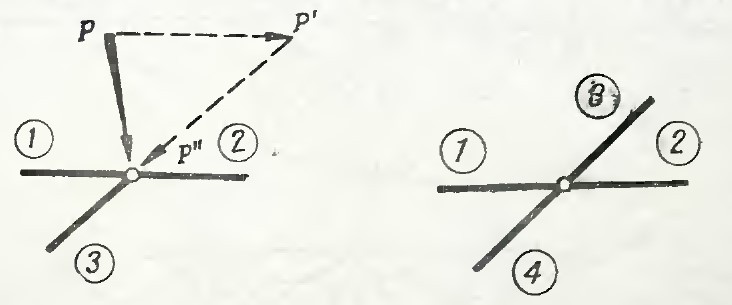
Рисунок 8​

• В ненагруженном узле из четырёх стержней, оси которых направлены по двум прямым, усилия будут попарно равны N(1) = N(2), N(3) = N(4).

Пользуясь методом вырезания узлов и зная правила нулевого стержня, можно проводить проверку расчётов, проведённых другими методами.

Расчёт ферм на персональном компьютере

Современные вычислительные комплексы основаны на методе конечного элемента. С их помощью осуществляют расчёты ферм любого очертания и геометрической сложности. Профессиональные программные пакеты Stark ES, SCAD Office, ПК Лира обладают широким функционалом и, к сожалению, высокой стоимостью, а также требуют глубокого понимания теории упругости и строительной механики. Для учебных целей и подойдут бесплатные аналоги, например Полюс 2.1.1.

В Полюсе можно рассчитывать плоские статически определимые и неопределимые стержневые конструкции (балки, фермы, рамы) на силовое воздействие, определять перемещения и температурное воздействие. Перед нами эпюра продольных усилий для фермы, изображённой на рис. 2. Ординаты графика совпадают с полученными вручную результатами.

Рисунок 9

Порядок работы в программе Полюс

• На панели инструментов (слева) выбираем элемент «опора». Размещаем помещаем элементы на свободное поле кликом левой кнопки мыши. Чтобы указать точные координаты опор, переходим в режим редактирования, нажав на значок курсора на панели инструментов.
• Двойной клик по опоре. Во всплывающем окне «свойства узла» задаём точные координаты в метрах. Положительное направление осей координат — вправо и вверх соответственно. Если узел не будет использоваться в качестве опоры, установите флажок «не связан с землёй». Здесь же можно задать приходящие в опору нагрузки в виде точечной силы или момента, а также перемещения. Правило знаков такое же. Удобно разместить крайнюю левую опору в начале координат (точка 0, 0).
• Далее размещаем узлы фермы. Выбираем элемент «свободный узел», кликаем по свободному полю, точные координаты прописываем для каждого узла в отдельности.
• На панели инструментов выбираем «стержень». Кликаем на начальном узле, отпускаем кнопку мышки. Затем кликаем на конечном узле. По умолчанию стержень имеет шарниры на двух концах и единичную жёсткость. Переходим в режим редактирования, двойным кликом по стержню открываем всплывающее окно, при необходимости изменяем граничные условия стержня (жёсткая связь, шарнир, подвижный шарнир для опорного конца) и его характеристики.
• Для загружения ферм используем инструмент «сила», нагрузка прикладывается в узлах. Для сил, прикладываемых не строго вертикально или горизонтально, устанавливаем параметр «под углом», после чего вводим угол наклона к горизонтали. Альтернативно можно сразу ввести значение проекций силы на ортогональные оси.
• Программа считает результат автоматически. На панели задач (вверху) можно переключать режимы отображения внутренних усилий (M, Q, N), а также опорных реакций (R). Результатом будет эпюра внутренних усилий в заданной конструкции.

В качестве примера рассчитаем сложную раскосную ферму, рассмотренную в методе моментной точки (рис. 6). Примем размеры и нагрузки: d = 3м, h = 6м, P = 100Н. По выведенной ранее формуле значение усилия в верхнем поясе фермы будет равно:

O(7−9) = -8d∙P/h = -8∙3м∙100Н/6м = -400 Н (сжатие)

Эпюра продольных усилий, полученная в Полюсе:

Рисунок 10

Значения совпадают, конструкция смоделирована верно.

Список литературы

1. Дарков А. В., Шапошников Н. Н. — Строительная механика: учебник для строительных специализированных вузов — М.: Высшая школа, 1986.
2. Рабинович И. М. — Основы строительной механики стержневых систем — М.: 1960.

Зачастую у нас нету возможности применить обычную балку для того или иного строения, и мы вынуждены применять более сложную конструкцию, которая называется ферма.

Расчет металлической фермы хоть и отличается от расчета балки, но нам не составит труда ее рассчитать. От вас будет требоваться лишь внимание, начальные знания алгебры и геометрии и час-два свободного времени.

Итак, начнем. Перед тем, как рассчитывать ферму, давайте зададимся какой-нибудь реальной ситуацией, с которой вы бы могли столкнуться. Например, вам необходимо перекрыть гараж шириной 6 метров и длиной 9 метров, но ни плит перекрытия, ни балок у вас нету. Только металлические уголки различных профилей. Вот из них мы и будем собирать нашу ферму!

В последующем на ферму будут опираться прогоны и профнастил. Опирание фермы на стены гаража – шарнирное.

Для начала вам необходимо будет узнать все геометрические размеры и углы вашей фермы. Здесь нам и понадобится наша математика, а именно — геометрия. Углы находим при помощи теоремы косинусов.

Затем нужно собрать все нагрузки на вашу ферму (посмотреть можно в статье Расчет навеса). Пусть у вас получился следующий вариант загружения:

Далее нам нужно пронумеровать все элементы, узлы фермы и задать опорные реакции (элементы подписаны зеленым, а узлы голубым).

Чтобы найти наши реакции, запишем уравнения равновесия усилий на ось y и уравнение равновесия моментов относительно узла 2.

Ra+Rb-100-200-200-200-100=0;
200*1,5 +200*3+200*4,5+100*6-Rb*6=0;

Из второго уравнения находим опорную реакцию Rb:

Rb=(200*1,5 +200*3+200*4,5+100*6) / 6;
Rb=400 кг

Зная, что Rb=400 кг, из 1-ого уравнения находим Ra:

Ra=100+200+200+200+100-Rb;
Ra=800-400=400 кг;

После того, как опорные реакции известны, мы должны найти узел, где меньше всего неизвестных величин (каждый пронумерованный элемент — это неизвестная величина). С этого момента мы начинаем разделять ферму на отдельные узлы и находить внутренние усилия стержней фермы в каждом из этих узлов. Именно по этим внутренним усилиям мы и будем подбирать сечения наших стержней.

Итак, перейдем к расчету. В узле 1 всего 2 неизвестных величины, поэтому рассмотрим этот узел (направления усилий S1 и S2 задаем из своих соображений, в любом случае у нас по итогу получится правильно).

Рассмотрим уравнения равновесия на оси х и у.

S2 * sin82,41 = 0; — на ось х
-100 + S1 = 0; — на ось y

Из 1-ого уравнения видно, что S2=0, то есть 2-ой стержень у нас не загружен!

Из 2-ого уравнения видно, что S1=100 кг.

Зная направление усилия S1, мы можем представить, что из себя представляет 1-ый стержень.

Поскольку одно усилие было направлено в узел (узел 1), то и второе усилие будет направлено в узел (узел 2). Значит наш стержень старается растянуться, а значит он сжат.

Далее рассмотрим узел 2. В нем было 3 неизвестных величины, но поскольку мы уже нашли значение и направление S1, то остается только 2 неизвестных величины.

Опять же составим уравнения на оси х и у:

-100 + 400 – sin33,69 * S3 = 0 — на ось у
— S3 * cos33,69 + S4 = 0 — на ось х

Из 1-ого уравнения S3 = 540,83 кг (стержень №3 сжат).

Из 2-ого уравнения S4 = 450 кг (стержень №4 растянут).

Рассмотрим 8-ой узел:

Составим уравнения на оси х и у:

-100 + S13 = 0 — на ось у
-S11 * cos7,59 = 0 — на ось х

Отсюда:

S13 = 100 кг (стержень №13 сжат)
S11 = 0 (нулевой стержень, никаких усилий в нем нету)

Рассмотрим 7-ой узел:

Составим уравнения на оси х и у:

-100 + 400 – S12 * sin21,8 = 0 — на ось у
S12 * cos21,8 — S10 = 0 — на ось х

ИЗ 1-ого уравнения находим S12:

S12 = 807,82 кг (стержень №12 сжат)

Из 2-ого уравнения находим S10:

S10 = 750,05 кг (стержень №10 растянут)

Дальше рассмотрим узел №3. Насколько мы помним 2-ой стержень у нас нулевой, а значит рисовать его не будем.

Уравнения на оси х и у:

-200 + 540,83 * sin33,69 – S5 * cos56,31 + S6 * sin7,59 = 0 — на ось y
540,83 * cos33,69 – S6 * cos7,59 + S5 * sin56,31 = 0 — на ось х

А здесь нам уже понадобится алгебра. Я не буду подробно расписывать методику нахождения неизвестных величин, но суть такова – из 1-ого уравнения выражаем S5 и подставляем ее во 2-ое уравнение.

По итогу получим:

S5 = 360,56 кг (стержень №5 растянут)
S6 = 756,64 кг (стержень №6 сжат)

Рассмотрим узел №6:

Составим уравнения на оси х и у:

-200 – S8 * sin7,59 + S9 * sin21,8 + 807,82 * sin21,8 = 0 — на ось у
S8 * cos7,59 + S9 * cos21,8 – 807,82 * cos21,8 = 0 — на ось х

Так же, как и в 3-ем узле найдем наши неизвестные.

S8 = 756,64 кг (стержень №8 сжат)
S9 = 0 кг (стержень №9 нулевой)

Рассмотрим узел №5:

Составим уравнения:

-200 + S7 – 756,64 * sin7,59 + 756,64 * sin7,59 = 0 — на ось у
756,64 * cos7,59 – 756,64 * cos7,59 = 0 — на ось х

Из 1-ого уравнения находим S7:

S7 = 200 кг (стержень №7 сжат)

В качестве проверки наших расчетов рассмотрим 4-ый узел (усилий в стержне №9 нету):

Составим уравнения на оси х и у:

-200 + 360,56 * sin33,69 = 0 — на ось у
-360,56 * cos33,69 – 450 + 750,05 = 0 — на ось х

В 1-ом уравнении получается:

0=0;

Во 2-ом уравнении:

0=0,05;

Данная погрешность допустима и связана скорее всего с углами (2 знака после запятой вместо 3-ех).

По итогу у нас получатся следующие значения:

Решил перепроверить все наши расчеты в программе и получил точно такие же значения:

Подбор сечения элементов фермы

При расчете металлической фермы после того, как все внутренние усилия в стержнях найдены, мы можем приступать к подбору сечения наших стержней.

Для удобства все значения сведем в таблицу.

Для расчетов нам понадобится не фактическая длина, а расчетная. Расчетную длину мы сможем найти в СНиП II-23-81* «Стальные конструкции». Таблица приведена ниже:

Как видно из таблицы, мы будем проверять стержень фермы в двух направлениях:

— в плоскости фермы

— из плоскости фермы (перпендикулярно плоскости фермы)

Чтобы найти расчетную длину стержня из плоскости фермы, нам нужно посмотреть, через какое расстояние этот стержень раскреплен с другой фермой. Например, по верхнему поясу наша ферма раскреплена связью/прогоном с другой фермой по центру. Значит расчетная длина верхнего пояса равна половине его длины. Если же верхний пояс раскреплен из плоскости в каждом узле, то расчетная длина стержня из плоскости такая же, как и в плоскости, и равна значениям в таблице выше.

Дальше, в зависимости от того сжат стержень или нет, по формуле мы рассчитываем необходимую площадь поперечного сечения.

При расчете сжатых стержней мы пользуемся формулой (необходимая площадь стержня):

По данной формуле можно рассчитать в этом онлайн расчете.

А также проверяем наш стержень на максимальную гибкость. Как правило, максимальная гибкость не должна быть больше 100-150.

Где lx – расчетная длина в плоскости фермы

Ly – расчетная длина из плоскости фермы

Ix – радиус инерции сечения вдоль оси х

Iy – радиус инерции сечения вдоль оси у

При расчете растянутых стержней мы пользуемся следующей формулой (необходимая площадь стержня):

Данной формулой можно воспользоваться в онлайн расчете растянутых элементов.

Например, два спаренных уголка 32х3 выдержат усилие равное 3.916*2 = 7,832 т.