Работа силы упругости при растяжении
Сила – это количественная мера взаимодействия тел. В рамках классической механики мы имеем дело со следующими видами сил: силами инерции, гравитационными, электростатическими, упругими, силами трения и сопротивления. Объектами воздействия классических сил являются м.т., с.м.т., твердое тело, сплошная среда (твердое вещество, газ, жидкость).
Силы упругости, силы трения и сопротивления определяются взаимодействиеями между молекулами вещества и имеют в своей основе электромагнитное происхождение и действуют в масштабах межмолекулярных расстояний.
Закон Гука
Закон Гука применим к деформируемым объектам, возвращающимся к исходному состоянию после снятия силы. Например, для растягивающейся пружины справедлива формула силы
F = kx, (1)
где F – действующая сила,
k – коэффициент пропорциональности, или жесткость пружины,
x – растяжение пружины.
Кроме линейных объектов типа пружины, на практике встречается множество других типов деформируемых объектов, по отношению к которым можно применять закон Гука. Только в этом случае коэффициент k может быть тензором 2–го порядка соответствующей размерности. Движение при этом обратимо.
Деформацией называют изменение формы, размеров или объема тела. Деформация может быть вызвана действием на тело приложенных к нему внешних сил. Если после прекращения действия сил тело возвращается в прежнее состояние (деформация исчезает), то деформация называется упругой. Деформации, сохраняющиеся и после того, как внешние силы перестали действовать на тело – пластическими. Обычно деформация бывает упругой, если ее величина не превосходит определенного предела (предела упругости). Внутри такого деформированного тела возникают силы, называемые силами упругости.
Различают деформации растяжения или сжатия (одностороннего или всестороннего), изгиба, кручения и сдвига.
Силы упругости действуют в любом сечении деформированного тела, а также в месте его контакта с телом, вызывающим деформации. В случае одностороннего растяжения или сжатия сила упругости направлена вдоль прямой, по которой действует внешняя сила, вызывающая деформацию тела, противоположно направлению этой силы и перпендикулярно поверхности тела.
Природа упругих сил электрическая. При деформациях твердого тела его частицы (атомы, молекулы, ионы), находящиеся в узлах кристаллической решетки, смещаются из своих положений равновесия. Этому смещению противодействуют силы взаимодействия между частицами твердого тела, удерживающие эти частицы на определенном расстоянии друг от друга. Поэтому при любом виде упругой деформации в теле возникают внутренние силы, препятствующие его деформации. Связь между силой упругости и упругой деформацией тела (при малых деформациях) была экспериментально установлена английским физиком Гуком.
Закон Гука для одностороннего растяжения (сжатия) формулируют так: сила упругости, возникающая при деформации тела, пропорциональна удлинению этого тела. Опытным путем установлено, что при малых деформациях упругая сила пропорциональна величине деформации. Например, при растяжении пружины на величину Δlупругая сила F вдоль оси пружины будет равна
F = –kΔl, (2)
где F – сила упругости;
Δl – удлинение (деформация) тела;
k – коэффициент пропорциональности, зависящий от размеров и материала тела, называемый жесткостью. Единица жесткости в СИ – ньютон на метр (Н/м).
Знак «–» в формуле (2) указывает, что направление силы противоположно направлению деформации (при растяжении пружины сила F сжимает ее и наоборот, при сжатии растягивает).
Упругую силу принято характеризовать не ее непосредственной величиной F, а отношением F к площади поверхности S, через которую она действует. Это отношение называют напряжением. В случае, когда сила F перпендикулярна поверхности S, напряжение называют нормальным. Его обозначают σ. Напряжение измеряют в паскалях [Па]. (1 Па = 1 Н / 1 м2).
Деформацию твердых тел чаще характеризуют не абсолютным изменением длины Δl, а относительным удлинением ε (3)
где l – длина тела. ε – безразмерная величина.
При малых деформациях относительное удлинение пропорционально нормальному напряжению. Эту связь деформации и напряжения также называют законом Гука. Его принято записывать в следующей форме (4):
Коэффициент пропорциональности Е в законе Гука характеризует упругость данного материала и называется модулем (продольной) упругости (модулем Юнга). Модуль Юнга численно равен такому нормальному напряжению, которое должно было бы возникнуть в теле при увеличении его длины в 2 раза (если бы для такой большой деформации выполнялся закон Гука). Модуль упругости выражается в паскалях.
Диаграмма растяжения
Используя формулу (3), (4), по экспериментальным значениям относительного удлинения ε можно вычислить соответствующие им значения нормального напряжения σ, возникающего в деформированном теле, и построить график зависимости σ от ε. Этот график называют диаграммой растяжения. Подобный график для металлического образца изображен на рис. 1.
Рис. 1. График деформации реального тела.
На участке 0–1 график имеет вид прямой, проходящей через начало координат. Это значит, что до определенного значения напряжения σп деформация является упругой и выполняется закон Гука, т. е. нормальное напряжение пропорционально относительному удлинению. Максимальное значение нормального напряжения σп, при котором еще выполняется закон Гука, называют пределом пропорциональности.
При дальнейшем увеличении нагрузки зависимость напряжения от относительного удлинения становится нелинейной (участок 1–2), хотя упругие свойства тела еще сохраняются. Максимальное значение нормального напряжения, при котором еще не возникает остаточная деформация, называют пределом упругости. (Предел упругости лишь на сотые доли процента превышает предел пропорциональности.) Увеличение нагрузки выше предела упругости (участок 2–3) приводит к тому, что деформация становится остаточной.
Затем образец начинает удлиняться практически при постоянном напряжении (участок 3–4 графика). Это явление называют текучестью материала. Нормальное напряжение σт, при котором остаточная деформация достигает заданного значения, называют пределом текучести.
При напряжениях, превышающих предел текучести, упругие свойства тела в известной мере восстанавливаются, и оно вновь начинает сопротивляться деформации (участок 4–5 графика). Максимальное значение нормального напряжения σпр, при превышении которого происходит разрыв образца, называют пределом прочности.
Таблица 1. Пример таблицы модулей упругости металлов
—————————————————————————————-
Ссылка на мою статью Как написать формулы в статье на Дзен?
Мои странички на Дзен: https://zen.yandex.ru/id/5e036c95fc69ab00aecfe6e9
Если хотите узнать, что обозначает слово или словосочетание, в ОПЕРЕ выделите это слово(сочетание), нажмите правую клавишу мыши и выберите «Искать в …», далее — «Yandex». Если это текстовая ссылка – выделите ее, нажмите правую клавишу мыши, выберите «перейти …». Все! О-ля-ля!
Если вам понравилась статья, то поставьте «лайк» и подпишитесь на канал! Если не понравилась – все равно комментируйте и подписывайтесь. Этим вы поможете каналу. И делитесь ссылками в ваших соцсетях!
Источник
Тема: «Работа силы тяжести. Работа силы упругости. Потенциальная энергия»
Физика 10 класс
Цели урока: Сформировать знания по новой теме в соответствии с программным материалом, дать определение потенциальной энергии, показать, что изменение энергии при переходе из одного состояния в другое равно работе внешних сил. Привлечь к проведению анализа, сравнения, формулировке выводов. Формировать интерес к познаниям законов природы.
Ход урока:
1. Организационный момент
2. Проверка домашнего задания:
Задача
Сани тянут на пути 100 м с силой 80 Н за веревку, составляющую угол 30° к горизонту. Какая работа совершается при этом?
Задача
Равнодействующая сил, действующих на тело, равна 20 Н и направлена горизонтально. Тело движется так, что его координата изменяется по закону x = 10 + 2t + t2. Какую работу совершает сила за 4 с?
Актуализация знаний.
Что называют механической работой?
В каком случае о силе можно сказать, что она совершает работу?
В каком случае работа положительна, в каком отрицательна, в каком равна нулю?
Чему равна работа силы тяжести по замкнутому пути?
По какой формуле можно вычислить работу силы?
Что общего между работой силы тяжести и силы упругости?
Открытие нового знания
Работа силы тяжести.
Модуль перемещения тела |Δ| = h1- h2.
Направления векторов силы тяжести T и перемещения Δ совпадают. Согласно определению работы (см. формулу (5.2)) имеем
А = |Т| |Δ|cos0° = mg(h1 — h2) = mgh1 — mgh2.
Пусть теперь тело бросили вертикально вверх из точки, расположенной на высоте h1 над поверхностью Земли, и оно достигло высоты h2 (рис. 5.9). Векторы Т и Δ направлены в противоположные стороны, а модуль перемещения |Δ| = h2 — h1. Работу силы тяжести запишем так:
А = |Т| |Δ|cos180° = -mg(h2 — h1) = mgh1 — mgh2.
Если же тело перемещается по прямой так, что направление перемещения составляет угол а с направлением силы тяжести (рис. 5.10), то работа силы тяжести равна:
А = |Т| |Δ|cosα = mg|BC|cosα.
Из прямоугольного треугольника BCD видно, что |BC|cosα = BD = h1 — h2. Следовательно,
А = mg(h1 — h2) = mgh1 — mgh2.
При прямолинейном движении тела работа силы тяжести в каждом случае равна разности двух значений величины, зависящей от положений тела, определяемых высотами h1 и h2 над поверхностью Земли.
Более того, работа силы тяжести при перемещении тела массой т из одного положения в другое не зависит от формы траектории, по которой движется тело.
А = mgh1 — mgh2.
Определим работу А при перемещении тела по замкнутому контуру, например по контуру BCDEB. Работа А1 силы тяжести при перемещении тела из точки В в точку D по траектории BCD: А1 = mg(h2 — h1), по траектории DEB: А2 = mg(h1 — h2).
Тогда суммарная работа А = А1 + А2 = mg(h2 — h1) + mg(h1 — h2) = 0. При движении тела по замкнутой траектории работа силы тяжести равна нулю.
Силы, работа которых не зависит от формы траектории точки приложения силы и по замкнутой траектории равна нулю, называют консервативными силами.
Работа силы упругости.
Если пружина растянута, то она действует на шар с силой 1 (рис. 5.13, б). модуль перемещения равен: |Δ| = х1 — х2
Работа может быть определена по графику зависимости Fx от х и что эта работа численно равна площади заштрихованной фигуры
Согласно закону Гука значения сил упругости F1 = kx1 и F2 = kx2. Подставляя эти выражения в уравнение (5.16) и учитывая, что |Δ| = х1 — х2, получаем
Или окончательно
Работа силы упругости при растяжении пружины, т. е. когда направление силы противоположно перемещению тела: Если начальное и конечное состояния пружины совпадают, то суммарная работа силы упругости при деформации пружины равна нулю.
Работа силы упругости не зависит от формы траектории и, так же как и сила тяжести, сила упругости является консервативной.
Потенциальная энергия
Согласно теореме об изменении кинетической энергии работа силы, действующей на тело, равна изменению его кинетической энергии:
Из формул (5.18) и (5.19) следует, что
Величину, равную произведению массы m тела на ускорение свободного падения g и на высоту h тела над поверхностью Земли, называют потенциальной энергией тела в поле силы тяжести и обозначают Еп: Еп = mgh. (5.20)
Величину, равную половине произведения коэффициента упругости k тела на квадрат удлинения или сжатия х, называют потенциальной энергией упруго деформированного тела: Еп=
Введя понятие потенциальной энергии, мы получаем возможность выразить работу любых консервативных сил через изменение потенциальной энергии. Под изменением величины понимают разность между её конечным и начальным значениями, поэтому Еп = Еп2 — Еп1.
Изменение потенциальной энергии тела равно работе консервативной силы, взятой с обратным знаком.
Нулевой уровень потенциальной энергии. Согласно уравнению (5.22) работа консервативных сил определяет не саму потенциальную энергию, а её изменение.
Поскольку работа определяет лишь изменение потенциальной энергии, то только изменение энергии в механике имеет физический смысл. Поэтому можно произвольно выбрать состояние системы, в котором её потенциальная энергия считается равной нулю. Этому состоянию соответствует нулевой уровень отсчёта потенциальной энергии.
Ни одно явление в природе или технике не определяется значением самой потенциальной энергии. Важна лишь разность значений потенциальной энергии в конечном и начальном состояниях системы тел.
Выбор нулевого уровня производится по-разному и диктуется условиями данной задачи. Обычно в качестве состояния с нулевой потенциальной энергией выбирают состояние системы с минимальным значением энергии. Тогда потенциальная энергия всегда положительна или равна нулю. Изолированная система тел стремится к состоянию, в котором её потенциальная энергия минимальна.
Если не удерживать тело, то оно падает на землю (h = 0); если отпустить растянутую или сжатую пружину, то она вернётся в недеформированное состояние (х = 0).
Закрепление
А1. Легковой автомобиль и автокран движутся по мосту, причём масса автокрана 4500 кг. Чему равна масса легкового автомобиля, если отношение потенциальной энергии автокрана и легкового автомобиля относительно уровня воды равно 3?
1) 500 кг 2) 1000 кг 3) 1500 кг 4) 3400 кг
А2. На рисунке представлена траектория движения тела, брошенного под углом к горизонту. В какой из четырёх точек, отмеченных на траектории, потенциальная энергия имеет минимальное значение?
1) 1 2) 2 3) 3 4) 4
А3. Математический маятник колеблется между точками А и С с периодом Т. В начальный момент времени маятник находится в точке А (см. рис.). Через какой промежуток времени его потенциальная энергия в первый раз достигнет минимального значения? Сопротивление воздуха не учитывайте,
А4. При удлинении на 2 см стальная пружина имеет потенциальную энергию упругой деформации 4 Дж. Как изменится потенциальная энергия этой пружины при уменьшении удлинения на 1 см?
1) уменьшится на 1 Дж 3) уменьшится на 3 Дж
2) уменьшится на 2 Дж 4) уменьшится на 4 Дж
А5. При растяжении пружины на 0,1 м в ней возникает сила упругости, равная 2,5 Н. Определите потенциальную энергию этой пружины при растяжении на 0,08 м.
1) 25 Дж 2) 0,16 Дж 3) 0,08 Дж 4) 0,04 Дж
7. Итог урока
1. В чём состоит сходство кинетической энергии тела с потенциальной?
2. В чём состоит различие между кинетической энергией и потенциальной?
3. Может ли потенциальная энергия быть отрицательной?
4. Чему равна работа силы тяжести и силы упругости при перемещении тела по замкнутой траектории?
5. Какие силы называют консервативными? Каково их общее свойство?
Домашняя работа: §44, 45, 46
Источник
Сила упругости
Любое тело, когда его деформируют и оказывают внешнее воздействие, сопротивляется и стремиться восстановить прежние форму и размеры. Это происходит по причине электромагнитного взаимодействия в теле на молекулярном уровне.
Деформация — изменение положения частиц тела друг относительно друга. Результат деформации — изменение межатомных расстояний и перегруппировка блоков атомов.
Определение. Что такое сила упругости?
Сила упругости — сила, возникающая при деформации в теле и стремящаяся вернуть тело в начальное состояние.
Рассмотрим простейшие деформации — растяжение и сжатие
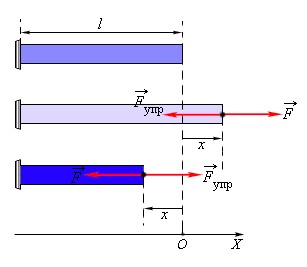
На рисунке показано, как действует сила упругости, когда мы сжимаем или растягиваем стержень.
Закон Гука
Для малых деформаций x≪ l справедлив закон Гука.
Закон Гука
Деформация, возникающая в упругом теле, пропорциональна приложенной к телу силе.
Fупр=-kx
Здесь k — коэффициент пропорциональности, называемый жесткостью. Единица измерения жесткости системе СИ Ньютон на метр. Жесткость зависит от материала тела, его формы и размеров.
Знак минус показывает, что сила упругости противодействует внешней силе и стремится вернуть тело в первоначальное состояние.
Существуют и другие формы записи закона Гука. Относительной деформацией тела называется отношение ε=xl. Напряжением в теле называется отношение σ=-FупрS. Здесь S — площадь поперечного сечения деформированного тела. Вторая формулировка закона Гука: относительная деформация пропорциональна напряжению.
ε=σE.
Здесь E — так называемый модуль Юнга, который не зависит от формы и размеров тела, а зависит только от свойств материала. Значение модуля Юнга для различных материалов широко варьируется. Например, для стали E≈2·1011 Нм2, а для резины E≈2·106 Нм2
Закон Гука можно обобщить для случая сложных деформаций. Рассмотрим деформацию изгиба стержня. При такой деформации изгиба сила упругости пропорциональна прогибу стержня.
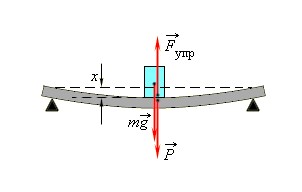
Концы стержня лежат на двух опорах, которые действуют на тело с силой N→, называемой силой нормальной реакции опоры. Почему нормальной? Потому что эта сила направлена перпендикулярно (нормально) поверхности соприкосновения.
Если стержень лежит на столе, сила нормальной реакции опоры направлена вертикально вверх, противоположно силе тяжести, которую она уравновешивает.
Вес тела — это сила, с которой оно действует на опору.
Силу упругости часто рассматривают в контексте растяжения или сжатия пружины. Это распространенный пример, который часто встречается не только в теории, но и на практике. Пружины используются для измерения величины сил. Прибор, предназначенный для этого — динамаметр.
Динамометр — пружина, растяжение которой проградуированно в единицах силы. Характерное свойство пружин заключается в том, что закон Гука для них применим при достаточно большом изменении длины.
При сжатии и растяжении пружины действует закон Гука, возникают упругие силы, пропорциональные изменению длины пружины и ее жесткости (коэффициента k).
В отличие от пружин стержни и проволоки подчиняются закону Гука в очень узких пределах. Так, при относительной дефомации больше 1% в материале возникают необратимые именения — текучесть и разрушения.
Источник
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Сила упругости — это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Силы, возникающие при пластических деформациях, не относятся к силам упругости.
Понятие о деформациях
Деформация — это изменение формы и размеров тела.
К деформациям относятся: растяжение, сжатие, кручение, сдвиг, изгиб.
Деформации бывают упругими и пластическими.
Закон Гука
Абсолютная величина силы упругости прямо пропорциональна величине деформации. В частности, для пружины, сжатой или растянутой на величину (displaystyle x) (разница между крайними положениями), сила упругости задается формулой [F=kx] где (displaystyle k) — коэффициент жесткости пружины.
Единицы измерения коэффициента жесткости: (k=)[Н/м].

Закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела.
Кубик массой (M = 2) кг, сжатый с боков пружинами, покоится на гладком горизонтальном столе. Первая пружина сжата на 2 см, а вторая сжата на 6 см. Жёсткость первой пружины (k_1 = 1200) Н/м. Чему равна жёсткость второй пружины (k_2)? Ответ выразите в Н/м.
По второму закону Ньютона силы упругости пружин будут уравновешивать друг друга, следовательно: [k_1Delta x_1=k_2Delta x_2] где (Delta x_1) и (Delta x_2) – сжатие первой и второй пружины соответственно.
Откуда жесткость второй пружины [k_2=dfrac{k_1 Delta x_1}{Delta x_2}= dfrac{1200text{ Н/м}cdot 2text{ см}}{6text{ см}}=400text{ Н/м}]
Ответ: 400
На штативе закреплён школьный динамометр. К нему подвесили груз массой 0,1 кг. Пружина динамометра при этом удлинилась на 2,5 см. Чему будет равно удлинение пружины, если масса груза увеличится втрое? (Ответ дайте в сантиметрах)
Согласно закону Гука [F=kDelta x] где k – жесткость пружины, ( Delta x) – удлинение пружины.
Найдем жесткость пружины, зная, что ( Delta x) = 2,5 см = 0,025 м при приложении силы, равно ( F=m_1g=0,1cdot 10=1text{ H} ): [k=dfrac{F}{Delta x}=dfrac{1}{0,025}=40text{ H/кг}] Если массу груза увеличить в 3 раза, то есть, (m_2=0,3) кг, то удлинение пружины будет равно: [Delta x=dfrac{F}{k}=dfrac{m_2g}{k}=dfrac{3cdot0,1cdot10text{ H}}{40text{ H/кг}}=0,075text{ м}=7,5text{ см}]
Ответ: 7,5
К системе из кубика массой M = 3 кг и двух пружин приложена постоянная горизонтальная сила F величиной 20 Н (см. рисунок). Между кубиком и опорой трения нет. Система покоится. Жёсткость первой пружины (k_1 = 400 text{ Н/м}). Жёсткость второй пружины (k_2 = 800 text{ Н/м}). Каково удлинение первой пружины? (Ответ дайте в сантиметрах)
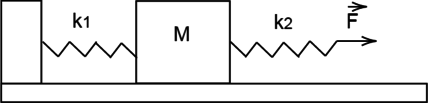
Согласно закону Гука удлинение (Delta x) пружины связано с ее жесткостью k и приложенной к ней силе F выражением (F=kDelta x). На первую пружину действует такая же сила F, что и на вторую, так как трения между кубиком и опорой нет. То, что первая пружина соединена со второй через кубик, здесь не имеет никакого значения, соответственно удлинение первой пружины – это величина, равная: [Delta x=dfrac{F}{k_1}=dfrac{20text{ H}}{400text{ H/м}}=0,05 text{ м}=5 text{ см}]
Ответ: 5
Определите силу, под действием которой пружина жёсткостью 200 Н/см удлинится на 5 мм.
Согласно закону Гука ( F=kDelta x ), где k – жесткость пружины, ( Delta x) – удлинение пружины, получаем: [F=kDelta x=(dfrac{200}{0,01})text{H/м}cdot(5cdot10^{-3})text{м}=100text{ H}]
Ответ: 100
Пружина одним концом прикреплена к неподвижной опоре, к другому концу приложили силу равную 1500 Н, при этом пружина растянулась на 0,2 м. Определите жесткость данной пружины. Ответ дать в Н/м.
После растяжения, пружина покоится и на неё действуют 2 силы направленные в противоположные направления: (F_{text{упр}}) – сила упругости и F – приложенная сила.
Тогда по первому закону Ньютона: [F_{text{упр}}=F] По закону Гука: [F_{text{упр}}=kx] Приравниваем эти формулы: [F=kx] Тогда [k=frac{F}{x}=frac{1500}{0,2}=7500 text{ Н/м}]
Ответ: 7500
К потолку прикреплены одним концом две пружины с одинаковой жесткостью. За другой конец первую пружину растягивают с силой (F_{text{1}}), которая в 2,5 раза больше силы (F_{text{2}}), растягивающей вторую пружину. При этом вторая пружина растянулась на 0,4 м. Насколько растянулась первая пружина? Ответ дать в метрах.
После растяжения обе пружины находятся в покое и на них, кроме данных сил действует сила упругости. Тогда по первому закону Ньютона: [F_{text{упр1}}=F_{text{1}}] [F_{text{упр2}}=F_{text{2}}] где (F_{text{упр1}}) – сила упругости, действующая на первую пружина, (F_{text{упр2}}) – на вторую.
По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [kx_{1}=F_{1}quad(1)] [kx_{2}=F_{text{2}}quad(2)] где (x_{1}) – удлинение первой пружины, (x_{2}) – второй. Разделим (1) на (2), получится: [frac{x_{1}}{x_{2}}=frac{F_{text{1}}}{F_{text{2}}}Rightarrow x_{1}=dfrac{F_{text{1}}x_{2}}{F_{text{2}}}=2,5cdot0,4=1text{ м}]
Ответ: 1
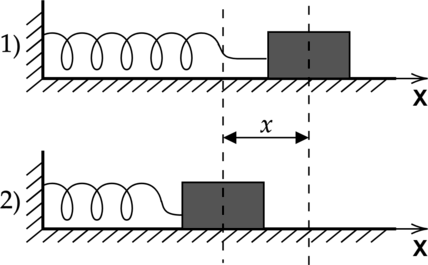
К грузу массой (m) аккуратно подвесили другой груз массой (M), при этом пружина с жесткостью 1200 Н/м удлинилась так, как показано на рисунке. Найдите массу (M). Ускорение свободного падения считать равным 10 м/(c^{2}). Ответ дать в кг.
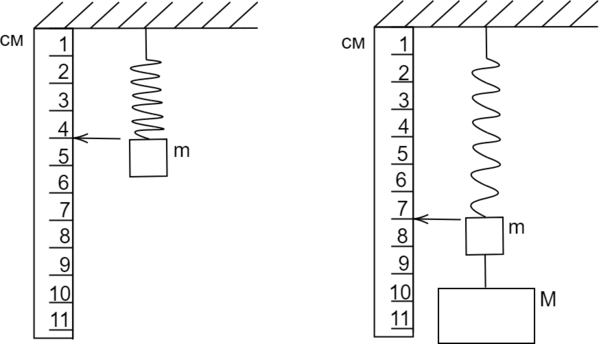
Рассмотрим ситуацию до подвешивания груза: система тел “груз и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg=F_{text{упр}1}] Рассмотрим ситуацию после подвешивания груза: систама тел “2 груза и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg+Mg=F_{text{упр2}}] По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [mg=kx_{1}quad(1)] [mg+Mg=kx_{2}quad(2)] Вычтем (1) из (2), получится: [Mg=k(x_{2}-x_{1})Rightarrow M=dfrac{k(x_{2}-x_{1})}{g}=frac{1200cdot0,03}{10}=3,6text{ кг}]
Ответ: 3,6
Источник
