Работа при растяжении пружины динамометра

1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Сила упругости — это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Силы, возникающие при пластических деформациях, не относятся к силам упругости.
Понятие о деформациях
Деформация — это изменение формы и размеров тела.
К деформациям относятся: растяжение, сжатие, кручение, сдвиг, изгиб.
Деформации бывают упругими и пластическими.
Закон Гука
Абсолютная величина силы упругости прямо пропорциональна величине деформации. В частности, для пружины, сжатой или растянутой на величину (displaystyle x) (разница между крайними положениями), сила упругости задается формулой [F=kx] где (displaystyle k) — коэффициент жесткости пружины.
Единицы измерения коэффициента жесткости: (k=)[Н/м].
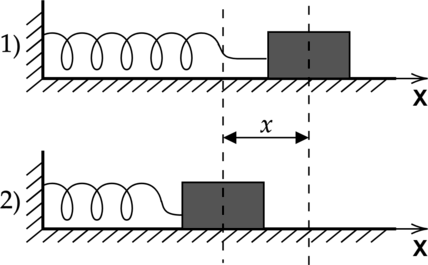
Закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела.
Кубик массой (M = 2) кг, сжатый с боков пружинами, покоится на гладком горизонтальном столе. Первая пружина сжата на 2 см, а вторая сжата на 6 см. Жёсткость первой пружины (k_1 = 1200) Н/м. Чему равна жёсткость второй пружины (k_2)? Ответ выразите в Н/м.
По второму закону Ньютона силы упругости пружин будут уравновешивать друг друга, следовательно: [k_1Delta x_1=k_2Delta x_2] где (Delta x_1) и (Delta x_2) – сжатие первой и второй пружины соответственно.
Откуда жесткость второй пружины [k_2=dfrac{k_1 Delta x_1}{Delta x_2}= dfrac{1200text{ Н/м}cdot 2text{ см}}{6text{ см}}=400text{ Н/м}]
Ответ: 400
На штативе закреплён школьный динамометр. К нему подвесили груз массой 0,1 кг. Пружина динамометра при этом удлинилась на 2,5 см. Чему будет равно удлинение пружины, если масса груза увеличится втрое? (Ответ дайте в сантиметрах)
Согласно закону Гука [F=kDelta x] где k – жесткость пружины, ( Delta x) – удлинение пружины.
Найдем жесткость пружины, зная, что ( Delta x) = 2,5 см = 0,025 м при приложении силы, равно ( F=m_1g=0,1cdot 10=1text{ H} ): [k=dfrac{F}{Delta x}=dfrac{1}{0,025}=40text{ H/кг}] Если массу груза увеличить в 3 раза, то есть, (m_2=0,3) кг, то удлинение пружины будет равно: [Delta x=dfrac{F}{k}=dfrac{m_2g}{k}=dfrac{3cdot0,1cdot10text{ H}}{40text{ H/кг}}=0,075text{ м}=7,5text{ см}]
Ответ: 7,5
К системе из кубика массой M = 3 кг и двух пружин приложена постоянная горизонтальная сила F величиной 20 Н (см. рисунок). Между кубиком и опорой трения нет. Система покоится. Жёсткость первой пружины (k_1 = 400 text{ Н/м}). Жёсткость второй пружины (k_2 = 800 text{ Н/м}). Каково удлинение первой пружины? (Ответ дайте в сантиметрах)
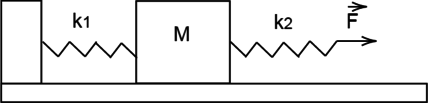
Согласно закону Гука удлинение (Delta x) пружины связано с ее жесткостью k и приложенной к ней силе F выражением (F=kDelta x). На первую пружину действует такая же сила F, что и на вторую, так как трения между кубиком и опорой нет. То, что первая пружина соединена со второй через кубик, здесь не имеет никакого значения, соответственно удлинение первой пружины – это величина, равная: [Delta x=dfrac{F}{k_1}=dfrac{20text{ H}}{400text{ H/м}}=0,05 text{ м}=5 text{ см}]
Ответ: 5
Определите силу, под действием которой пружина жёсткостью 200 Н/см удлинится на 5 мм.
Согласно закону Гука ( F=kDelta x ), где k – жесткость пружины, ( Delta x) – удлинение пружины, получаем: [F=kDelta x=(dfrac{200}{0,01})text{H/м}cdot(5cdot10^{-3})text{м}=100text{ H}]
Ответ: 100
Пружина одним концом прикреплена к неподвижной опоре, к другому концу приложили силу равную 1500 Н, при этом пружина растянулась на 0,2 м. Определите жесткость данной пружины. Ответ дать в Н/м.
После растяжения, пружина покоится и на неё действуют 2 силы направленные в противоположные направления: (F_{text{упр}}) – сила упругости и F – приложенная сила.
Тогда по первому закону Ньютона: [F_{text{упр}}=F] По закону Гука: [F_{text{упр}}=kx] Приравниваем эти формулы: [F=kx] Тогда [k=frac{F}{x}=frac{1500}{0,2}=7500 text{ Н/м}]
Ответ: 7500
К потолку прикреплены одним концом две пружины с одинаковой жесткостью. За другой конец первую пружину растягивают с силой (F_{text{1}}), которая в 2,5 раза больше силы (F_{text{2}}), растягивающей вторую пружину. При этом вторая пружина растянулась на 0,4 м. Насколько растянулась первая пружина? Ответ дать в метрах.
После растяжения обе пружины находятся в покое и на них, кроме данных сил действует сила упругости. Тогда по первому закону Ньютона: [F_{text{упр1}}=F_{text{1}}] [F_{text{упр2}}=F_{text{2}}] где (F_{text{упр1}}) – сила упругости, действующая на первую пружина, (F_{text{упр2}}) – на вторую.
По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [kx_{1}=F_{1}quad(1)] [kx_{2}=F_{text{2}}quad(2)] где (x_{1}) – удлинение первой пружины, (x_{2}) – второй. Разделим (1) на (2), получится: [frac{x_{1}}{x_{2}}=frac{F_{text{1}}}{F_{text{2}}}Rightarrow x_{1}=dfrac{F_{text{1}}x_{2}}{F_{text{2}}}=2,5cdot0,4=1text{ м}]
Ответ: 1
К грузу массой (m) аккуратно подвесили другой груз массой (M), при этом пружина с жесткостью 1200 Н/м удлинилась так, как показано на рисунке. Найдите массу (M). Ускорение свободного падения считать равным 10 м/(c^{2}). Ответ дать в кг.
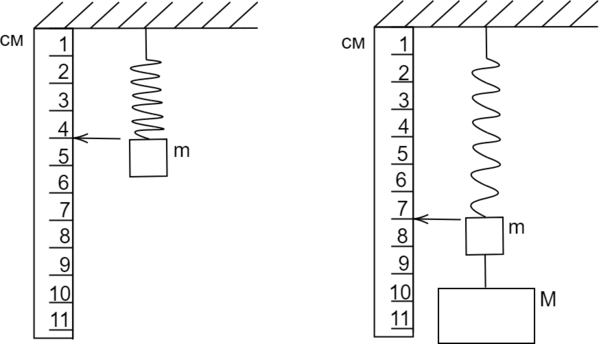
Рассмотрим ситуацию до подвешивания груза: система тел “груз и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg=F_{text{упр}1}] Рассмотрим ситуацию после подвешивания груза: систама тел “2 груза и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg+Mg=F_{text{упр2}}] По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [mg=kx_{1}quad(1)] [mg+Mg=kx_{2}quad(2)] Вычтем (1) из (2), получится: [Mg=k(x_{2}-x_{1})Rightarrow M=dfrac{k(x_{2}-x_{1})}{g}=frac{1200cdot0,03}{10}=3,6text{ кг}]
Ответ: 3,6
Источник
ПРУЖИННЫЕ ДИНАМОМЕТРЫ РАСТЯЖЕНИЯ ОБЩЕГО НАЗНАЧЕНИЯ (по ГОСТ 13837-79) [c.840]
Измерение растяжения пружины динамометра [c.29]
Прямоугольная рифленая пластинка 3 подвешена с помощью жесткой нити 4 к пружинному динамометру 6. Пластинку полностью погружают в исследуемую дисперсную систему, помещенную в кювету 2 до начала испытания. Кювету С дисперсной системой закрепляют на подъемном столике I. При опускании с постоянной скоростью столика с кюветой пружина растягивается и в системе возникает напряжение сдвига, которое, очевидно, пропорционально растяжению пружины. Последнее может быть измерено с помощью микроскопа 5, снабженного окулярным микрометром, или с помощью микрошкалы. [c.334]
Обычно пружины поставляют с техническим паспортом, в котором указывается величина максимально допустимой нагрузки, размер сжатия (растяжения) при этой нагрузке. Если таких данных не имеется, необходимо провести тарировку пружины. Устройство, применяемое для тарировки опорных пружин (рис. 40), состоит из сварного стола 1, направляющего стакана 3, приваренного к столу, и динамометра. Пружину 2 насаживают на стакан 3, замеряют ее высоту в свободном состоянии, после чего начинают затягивать регулировочную гайку, производя замеры высоты пружины и наблюдая за показаниями динамометра. На таком устройстве можно проверить пружины, рассчитанные на нагрузки свыше 1000 Н/см2. [c.73]
Изучение влияния растягивающих напряжений. При отсутствии в лаборатории специальных машин для растяжения металлов эту работу можно провести на самодельной установке, изготовленной из обычного штатива с тарированной пружиной (лучше с динамометром) или с грузом на тросике, перекинутом через блок. [c.52]
Особое место среди машин, предназначенных для испытания резины на растяжение, занимает динамометр Поляньи, в котором в качестве силоизмерителя применена плоская пружина.. [c.134]
При растяжении резиновых образцов их деформации несоизмеримо велйки по сравнению с прогибом пружины, так что последней можно пренебречь, считая положение верхнего зажима неизменным. Это обстоятельство позволяет использовать динамометр Поляньи для определения релаксации резины при растяжении, т. е. для замера изменения напряжения в резиновом образце при постоянном удлинении. Подобную задачу нельзя решить ни на одной из описанных выше машин. [c.135]
Напряжение растяжения в покрытии определяли по методике, описанной в работе [2], коррозию — по методике, описанной в настоящей главе, а адгезию — с помощью пружинного динамометра отслоением полоски изоляции, вырезанной шириной 1 см и растяжением ее под углом 180° к поверхности трубы. [c.46]
Здесь все величины выражены в единицах системы GS. На практике, разумеется, динамометр проще протарировать, подвешивая к нему различные разновески и наблюдая, какому весу груза соответствует то или иное растяжение пружины. После этого, пользуясь формулой (186), легко построить градуировочную кривую, показывающую, какой величине постоянной а поверхностного натяжения соответствует каждое положение максимального указателя на шкале. Для того чтобы шкала не была слишком длинной, а охватывала только необходимый диапазон растяжений пружины (соответственно пределам, в которых может колебаться поверхностное натяжение), пружине динамометра придано некоторое определенное начальное натяжение. Оно должно быть немного меньше того, которое необходимо для отрывания конуса при самом малом значении поверхностного натяжения, встречающемся в природе. [c.868]
В современных разрывных машинах электрические сигналы датчиков, пропорциональные удлинению и нагрузке, подаются на самописец, вычерчивающий непосредственно кривую растяжения. Продолжительность испытания определяется начальным расстоянием между зажимами и скоростью движения нижнего зажима, движущегося с помощью электромотора, а при высоких скоростях испытания — пневмо- или гидропривода. Примером может служить машина типа РИП-10 (рис. 125) для одноосного растяжения полимерных аленок в широком интервале температур и скоростей [84]. Шести-позиционная кассета 1 с укрепленными в ней с помощью зажимов 2 образцами пленки 3 обеспечивает их прогрев в термостате 4 перед испытанием. Верхние зажимы поочередно крепятся посредством тяг 5 и разъемного шарнира к пружинному динамометру (5. Динамометр соединен с подвижным ползунком 7, который перемещается по вертикали ходовым винтом 8. Тензодатчики, приклеенные к кольцу дина-.юметра, через усилитель передают сигнал самописцу 9. [c.219]
Измерение сил и крутящих моментов осуществляется при помощи соответствующих динамометров. Наилучшими приборами для измерения сил сжатия и растяжения являются механические динамометры типа плоских пружин или пружинных колец. Крутящие моменты измеряются посредством электрических крутильных динамо1 гетров—индуктивных, фотоэлектрических, с проволочными датчиками и т. п., а также путем измерения реактивных моментов на балапсирпо монтируемых электродвигателях или отдельных узлах испытательной машины. [c.298]
На рис. 34 через и обозначены две треугольные железные рамы. К их углам прицеплены. -образные крюки, связанные со спиральными пружинами типа обычных дверных пружин. Днина пружин до растяжения равна 38 см, а после растяжения—46 48 см. к нижнему треугольнику при помощи динамометров и упругих стержней или проволочек подвешена рама, состоящая из трех вертикальных стержней, прочно закрепленных концами в круглых пластинах. Для обеспечения необходимого веса на этих стержнях крепятся три коробки наполняемые свинцовой дробью. Положение и масса IV определяются условиями, нри которых центр колебаний рамы и гальванометра овпадает с точкой крепления нити гальванометра. Три скобы С Держат стержни на такой высоте, что точка крепления нити попадает в плоскость, образуемую этими тремя точками опоры рамы. Нч нижнюю плоскость рамы помещается свинцовая пластина. Пружины по всей длине туго обматываются липкой лентой так, [c.125]
Смотреть страницы где упоминается термин Динамометры пружинные растяжения:
[c.724]
Справочник конструктора-машиностроителя Том 3 Издание 8 (2001) — [
c.0
]
Источник
Подробности
Просмотров: 896
«Физика — 10 класс»
При решении задач по этой теме надо иметь в виду, что закон Гука справедлив только при упругих деформациях тел. Сила упругости не зависит от того, какая происходит деформация: сжатия или растяжения, она одинакова при одинаковых Δl. Кроме этого, считается, что сила упругости вдоль всей пружины одинакова, так как масса пружины обычно не учитывается.
Задача 1.
При помощи пружинного динамометра поднимают с ускорением а = 2,5 м/с2, направленным вверх, груз массой m = 2 кг. Определите модуль удлинения пружины динамометра, если её жёсткость k = 1000 Н/м.

Р е ш е н и е.
Согласно закону Гука, выражающему связь между модулем внешней силы  , вызывающей растяжение пружины, и её удлинением, имеем F = kΔl. Отсюда
, вызывающей растяжение пружины, и её удлинением, имеем F = kΔl. Отсюда 
Для нахождения силы  воспользуемся вторым законом Ньютона. На груз, кроме силы тяжести m
воспользуемся вторым законом Ньютона. На груз, кроме силы тяжести m , действует сила упругости пружины, равная по модулю F и направленная вертикально вверх. Согласно второму закону Ньютона m
, действует сила упругости пружины, равная по модулю F и направленная вертикально вверх. Согласно второму закону Ньютона m = F + m
= F + m .
.
Направим ось OY вертикально вверх так, чтобы пружина была расположена вдоль этой оси (рис. 3.16). В проекции на ось OY второй закон Ньютона можно записать в виде mау = Fy + mgy
Так как ау = a, gy = -g и Fy = F, то F = mа + mg = m(а + g).
Следовательно,

Задача 2.
Определите, как изменяется сила натяжения пружины, прикреплённой к бруску массой m = 5 кг, находящемуся неподвижно на наклонной поверхности, при изменении угла наклона от 30° до 60°. Трение не учитывайте.

Р е ш е н и е.
На брусок действуют сила тяжести, сила натяжения пружины и сила реакции опоры (рис. 3.17).
Условие равновесия бруска: m +
+  +
+  yпp = 0.
yпp = 0.
Запишем это условие в проекциях на оси ОХ и OY: 
Из первого уравнения системы получим Fyпp = mg sinα.
При изменении угла наклона изменение силы упругости найдём из выражения ΔFyпp = mg(sinα2 — sinα1) = 5 • 10 • (0,866 — 0,5) (Н) = 18,3 Н.
Задача 3.
К потолку подвешены последовательно две невесомые пружины жёсткостями 60 Н/м и 40 Н/м. К нижнему концу второй пружины прикреплён груз массой 0,1 кг. Определите жёсткость воображаемой пружины, удлинение которой было бы таким же, как и двух пружин при подвешивании к ней такого же груза (эффективную жёсткость).

Р е ш е н и е.
Так как весом пружин можно пренебречь, то очевидно, что силы натяжения пружин равны (рис. 3.18). Тогда согласно закону Гука
Fynp1 = Fупр2; k1x1 = k2х2. (1)
На подвешенный груз действуют две силы — сила тяжести и сила натяжения второй пружины.
Условие равновесия груза запишем в виде mg = k2х2.
Из этого уравнения найдём удлинение

Подставив выражение для х2 в уравнение (1), получим для удлинения

Определим теперь эффективную жёсткость. Запишем закон Гука для воображаемой пружины:

Подставив в формулу (2) выражения для удлинений x1 и х2 пружин, получим

Для эффективной жёсткости получим выражение

Задача 4.
Через блок, закреплённый у края стола, перекинута нерастяжимая нить, к концам которой привязаны брусок массой m1 = 1 кг, находящийся на горизонтальной поверхности стола, и пружина жёсткостью k = 50 Н/м, расположенная вертикально. Ко второму концу пружины привязана гиря массой m2 = 200 г (рис. 3.19). Определите удлинение пружины при движении тел. Силу трения, массы пружины, блока и нити не учитывайте.

Р е ш е н и е.
На брусок действуют сила тяжести, сила реакции опоры и сила натяжения нити.
На гирю действуют сила тяжести и сила натяжения пружины.
Согласно второму закону Ньютона для бруска и гири запишем:
m1 1 = m1
1 = m1 +
+  +
+  ;
;
m2 2 = m
2 = m +
+  упр.
упр.
В проекциях на выбранные оси координат запишем: на ось ОХ: m1а1 = Т;
на ось OY:

Так как нить нерастяжима, то модули ускорений равны: а1 = а2 = а.
В силу условия малых масс пружины, нити и блока можно записать: T2 = Fупр и Т1 = Т2 = Т.
Учтя последние равенства, систему уравнений (1) запишем в виде

Выразив ускорение из первого уравнения системы и подставив его во второе, получим

Из этого уравнения найдём силу натяжения нити:

Так как согласно закону Гука Fупр = kx, то

Тогда удлинение пружины

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Динамика — Физика, учебник для 10 класса — Класс!ная физика
Основное утверждение механики —
Сила —
Инертность тела. Масса. Единица массы —
Первый закон Ньютона —
Второй закон Ньютона —
Принцип суперпозиции сил —
Примеры решения задач по теме «Второй закон Ньютона» —
Третий закон Ньютона —
Геоцентрическая система отсчёта —
Принцип относительности Галилея. Инвариантные и относительные величины —
Силы в природе —
Сила тяжести и сила всемирного тяготения —
Сила тяжести на других планетах —
Примеры решения задач по теме «Закон всемирного тяготения» —
Первая космическая скорость —
Примеры решения задач по теме «Первая космическая скорость» —
Вес. Невесомость —
Деформация и силы упругости. Закон Гука —
Примеры решения задач по теме «Силы упругости. Закон Гука» —
Силы трения —
Примеры решения задач по теме «Силы трения» —
Примеры решения задач по теме «Силы трения» (продолжение) —
Источник
