Работа при растяжении пружины
Рассмотрим абсолютно неупругий удар двух шаров одинаковой массы, сделанных из пластилина. Если эти шары летят друг на друга с одной и той же скоростью, то при соударении они прилипнут друг к другу и остановятся. В этом случае суммарный импульс обоих шаров остался равным нулю, хотя состояние системы изменилось. Шары при этом нагрелись. Этот пример показывает, что импульс не всегда может служить мерой движения. Такой мерой является энергия. В данном случае механическая энергия при ударе перешла в другой вид энергии (тепловую).
Сначала рассмотрим важную характеристику — работу. Пусть материальная точка движется по траектории AB (рис. 1). На точку во время движения действует в общем случае переменная сила F. На участке ds (настолько малом, что модуль перемещения равен пройденному пути) силу F можно считать постоянной.

Рис 4.1. Элементарная работа
Элементарная работа силы  равна скалярному произведению вектора силы на вектор перемещения её точки приложения
равна скалярному произведению вектора силы на вектор перемещения её точки приложения 

Работа — скалярная величина, ее знак зависит от знака ![]() . Положительная работа совершается силой, если ее направление составляет острый угол
. Положительная работа совершается силой, если ее направление составляет острый угол  с направлением движения тела. Отрицательная работа совершается силой, направление которой составляет тупой угол
с направлением движения тела. Отрицательная работа совершается силой, направление которой составляет тупой угол  с направлением движения, при этом сила тормозит это движение. Величина
с направлением движения, при этом сила тормозит это движение. Величина

— это проекция силы F на направление перемещения. Следовательно,

Полная работа силы находится как сумма (интеграл) элементарных работ по всей траектории L точки:

При перемещении вдоль оси x работу графически можно представить как площадь под кривой Fx(x) (рис. 4.2), причем площади под осью абсцисс следует приписывать отрицательное значение.
Рис. 2. Графическая интерпретация работы силы. Здесь для краткости положено F = Fx(x)
Если перемещение ортогонально силе, то ![]() = 0 и работа равна нулю:
= 0 и работа равна нулю:

Последнее показывает, что понятие работы в механике отлично от обыденного представления о работе. Так, при перемещении груза с постоянной скоростью в горизонтальном направлении сила тяжести не совершает работы. Работа не совершается также и тогда, когда тело покоится, так как точка приложения силы не перемещается и  = 0. Здесь и ниже
= 0. Здесь и ниже  и
и  означают одно и то же — бесконечно малое перемещение, а |
означают одно и то же — бесконечно малое перемещение, а | |=|
|=| |=
|= — соответствующий бесконечно малый путь.
— соответствующий бесконечно малый путь.
Если на тело действует несколько сил, то

то есть работа результирующей нескольких сил равна алгебраической сумме работ, совершаемых каждой из сил в отдельности.
Рассмотрим для примера работу, совершаемую внешней силой по сжатию и растяжению пружины с жесткостью  . Направим ось 0x вдоль пружины, причем за начало координат выберем положение свободного конца пружины, находящейся в ненагруженном состоянии. Процесс сжатия/растяжения представляем как последовательность равновесных состояний: в каждый момент времени прилагаем внешнюю силу, равную по величине силе упругости со стороны пружины. Тогда согласно закону Гука
. Направим ось 0x вдоль пружины, причем за начало координат выберем положение свободного конца пружины, находящейся в ненагруженном состоянии. Процесс сжатия/растяжения представляем как последовательность равновесных состояний: в каждый момент времени прилагаем внешнюю силу, равную по величине силе упругости со стороны пружины. Тогда согласно закону Гука

где x — удлинение пружины. При положительных x (растяжение пружины) внешняя cила направлена направо, при отрицательных (сжатие) — налево (рис. 4.3).

Рис. 4.3. Работа, совершаемая при сжатии/растяжении пружины
Скалярное произведение для элементарной работы внешней силы имеет в этом случае вид

так что для полной работы упругой деформации пружины получаем

Заметим, что A не зависит от знака x: и при растяжении, и при сжатии пружины внешняя сила совершает одну и ту же положительную работу.
Дополнительная информация
https://www.plib.ru/library/book/17833.html – Хайкин С.Э. Физические основы механики, Наука, 1971 г.– стр. 476–479 (§ 111): выведено выражение для потенциальной энергии упруго деформированного тела.
Источник
- Авторы
- Резюме
- Файлы
Иванов Е.М.
Показано, что работа растяжения пружины A>kxm2 , где k — жесткость пружины, xm — максимальное растяжение. При вычислении работы надо использовать значения x и dx, полученные из решения уравнения движения.
Показано, что работа растяжения пружины A>kxm2 , где k — жесткость пружины, xm — максимальное растяжение. При вычислении работы надо использовать значения x и dx, полученные из решения уравнения движения.
It is shown, that work of a stretching of a spring A>kxm2 , where k — rigidity of a spring, xm — the maximal stretching. At calculation of work it is necessary to use values x and dx, the equations of movement received from the decision.
Рассмотрим спиральную пружину, один конец которой закреплен (рис. 1а), а к другому прикреплен груз массой m. Если пружину растянуть или сжать, то возникает сила F, стремящаяся вернуть тело в положение равновесия. При небольших растяжениях x справедлив закон Гука — сила пропорциональна растяжению пружины: F = -kx. Постоянная k называется коэффициентом упругости, или жесткостью пружины. Знак минус означает, что сила F направлена в сторону, противоположную смещению x, т.е. к положению равновесия x = 0. Геометрически (рис. 1b) , k = tgβ, xm — максимальное (амплитудное) растяжение пружины.
В курсах физики утверждается, что работа при растяжении от x = 0 до xm будет равна
(1)
и эта работа равна потенциальной энергии пружины, растянутой (или сжатой) на величину xm и обладающей жесткостью k. Однако это одно из заблуждений классической механики. Растягивающей силой, равной F = kx, нельзя растянуть пружину даже на долю микрона. Чтобы растянуть пружину, надо приложить растягивающую силу в виде (F1 + k1x ), где F1 >0 (рис. 2а). Уравнение движения (II закон Ньютона) запишем в следующем виде:
(2)
Решение при нулевых начальных условиях (при t = 0, x =0 и V =0) имеет вид
Из решения следует, что если F1 =0, то растяжения пружины не происходит. Амплитудные значения (при x = xm):
Работу вычисляем по формуле , где F = F1 — (k — k1)x, а x и dx определяются из выражений (3) и (4). Работа, совершаемая растягивающей силой
(5)
Работа, совершаемая силой упругости пружины
(6)
Из соотношения (5) следует, что работа, совершаемая растягивающей силой, не зависит от величин F1 и k1 и равна работе
(5а)
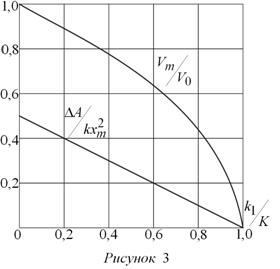
совершаемой постоянной силой F0, при этом работа, совершаемая силой упругости пружины A-0 = -kxm2 разность работ ΔA0 = kxm2 / 2 , конечная скорость при x = xm На рис. 3 даны графики зависимостей Vm / V0 и ΔA = kxm2 от величины отношения K1 / K. ΔA — кинетическая энергия груза.
Рассмотрим случай растягивающей силы FP > F0 (рис.2b) FP = F2 + k2x = F2 — b2x , где b2 = -k2 = tgα. Дифференциальное уравнение движения имеет вид:
(7)
Его решение при нулевых начальных условиях имеет вид:
; (8)
(9)
Амплитудные значения (при x = xm): xm = F2 / mω2; ; .
Работа, совершаемая растягивающей силой
(10)
Работа, совершаемая силой упругости пружины
(11)
Кинетическая энергия груза при x = xm
(12)
На рис. 4 даны графики изменения безразмерных комплексов ΔA / kxm2 и Vm / V0 в зависимости от величины отношения k2 / k.
Рассмотрим третий способ растяжения пружины с грузом (рис. 2с). Прикладываем растягивающую силу Fa >>F0 для растяжения пружины на некоторое расстояние xa, затем сила Fa отключается, а оставшийся отрезок пути, равный xm — xa, груз проходит по инерции, используя запас кинетической энергии Ka, приобретенный в точке xa. Для первого участка пути дифференциальное уравнение имеет вид
(13)
Его решение при нулевых начальных условиях:
; (14)
(15)
Время движения до x = xa
(16)
Работу вычисляем по формуле , где F(x) = Fa — kx, а x и dx определяются выражениями (14) и (15). Работа растяжения на участке до x = x0
(17)
Работа, совершаемая силой упругости пружины на этом же участке
(18)
Кинетическая энергия, приобретенная грузом:
(19)
Для второго участка уравнение движения имеет вид
(20)
Начальные условия для этого уравнения примем в виде: при t = 0 координата x = xa, скорость Va определяется выражением (15) при t = ta. Решение будет иметь вид:
(21)
(21a)
Работа силы упругости пружины на участке от x = xa до xm определится интегралом , где x и dx определяются выражениями (21) и (21а):
(22)
где tm ─ время движения груза от x=xa до x = xm. Условием достижения этой точки является равенство начальной кинетической энергии Ka работе силы упругости пружины A2. Это равенство сводится к трансцендентному уравнению
(23)
где a = kxa2 / 2; b = Ka — a; c = kxaVa / 2ω; φ = ωtm.
Приведем численный пример. Груз массой m = 1 кг, прикрепленный к пружине с жесткостью k = 400 Н/м, растягивается силой F0 = 80 Н на расстояние xm = 0,2. Работа силы растяжения Дж, работа силы упругости пружины Дж, время t = 0,0785 с.
Проведем растяжение силой Fa по схеме, показанной на рис. 2с. Расчет сведем в таблицу 1.
Таблица 1.
Fa [H] | Ka [Дж] | ta [c] | xa [м] | A+ [Дж] | A- [Дж] | tm [c] |
8000 | 8 | 0,0005 | 0,001 | 16 | -8 | 0,078 |
800 | 7 | 0,00468 | 0,00876 | 14,015 | -7,015 | 0,0762 |
200 | 6 | 0,0176 | 0,0309 | 12,19 | -6,19 | 0,0696 |
80 | 3,75 | 0,0377 | 0,054 | 8,088 | -4,338 | 0,0597 |
Таким образом, только в случае растяжения пружины с грузом по схеме, показанной на рис.2с, можно затратить работу на растяжение A+, близкую к потенциальной энергии растянутой пружины П = kxm2 / 2.
Библиографическая ссылка
Иванов Е.М. РАБОТА ДЕФОРМАЦИИ ПРУЖИННОГО МАЯТНИКА // Современные наукоемкие технологии. – 2007. – № 3. – С. 15-19;
URL: https://top-technologies.ru/ru/article/view?id=24676 (дата обращения: 16.07.2020).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Источник
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Сила упругости — это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Силы, возникающие при пластических деформациях, не относятся к силам упругости.
Понятие о деформациях
Деформация — это изменение формы и размеров тела.
К деформациям относятся: растяжение, сжатие, кручение, сдвиг, изгиб.
Деформации бывают упругими и пластическими.
Закон Гука
Абсолютная величина силы упругости прямо пропорциональна величине деформации. В частности, для пружины, сжатой или растянутой на величину (displaystyle x) (разница между крайними положениями), сила упругости задается формулой [F=kx] где (displaystyle k) — коэффициент жесткости пружины.
Единицы измерения коэффициента жесткости: (k=)[Н/м].
Закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела.
На штативе закреплён школьный динамометр. К нему подвесили груз массой 0,1 кг. Пружина динамометра при этом удлинилась на 2,5 см. Чему будет равно удлинение пружины, если масса груза увеличится втрое? (Ответ дайте в сантиметрах)
Согласно закону Гука [F=kDelta x] где k – жесткость пружины, ( Delta x) – удлинение пружины.
Найдем жесткость пружины, зная, что ( Delta x) = 2,5 см = 0,025 м при приложении силы, равно ( F=m_1g=0,1cdot 10=1text{ H} ): [k=dfrac{F}{Delta x}=dfrac{1}{0,025}=40text{ H/кг}] Если массу груза увеличить в 3 раза, то есть, (m_2=0,3) кг, то удлинение пружины будет равно: [Delta x=dfrac{F}{k}=dfrac{m_2g}{k}=dfrac{3cdot0,1cdot10text{ H}}{40text{ H/кг}}=0,075text{ м}=7,5text{ см}]
Ответ: 7,5
К системе из кубика массой M = 3 кг и двух пружин приложена постоянная горизонтальная сила F величиной 20 Н (см. рисунок). Между кубиком и опорой трения нет. Система покоится. Жёсткость первой пружины (k_1 = 400 text{ Н/м}). Жёсткость второй пружины (k_2 = 800 text{ Н/м}). Каково удлинение первой пружины? (Ответ дайте в сантиметрах)
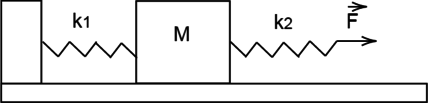
Согласно закону Гука удлинение (Delta x) пружины связано с ее жесткостью k и приложенной к ней силе F выражением (F=kDelta x). На первую пружину действует такая же сила F, что и на вторую, так как трения между кубиком и опорой нет. То, что первая пружина соединена со второй через кубик, здесь не имеет никакого значения, соответственно удлинение первой пружины – это величина, равная: [Delta x=dfrac{F}{k_1}=dfrac{20text{ H}}{400text{ H/м}}=0,05 text{ м}=5 text{ см}]
Ответ: 5
Определите силу, под действием которой пружина жёсткостью 200 Н/см удлинится на 5 мм.
Согласно закону Гука ( F=kDelta x ), где k – жесткость пружины, ( Delta x) – удлинение пружины, получаем: [F=kDelta x=(dfrac{200}{0,01})text{H/м}cdot(5cdot10^{-3})text{м}=100text{ H}]
Ответ: 100
Пружина одним концом прикреплена к неподвижной опоре, к другому концу приложили силу равную 1500 Н, при этом пружина растянулась на 0,2 м. Определите жесткость данной пружины. Ответ дать в Н/м.
После растяжения, пружина покоится и на неё действуют 2 силы направленные в противоположные направления: (F_{text{упр}}) – сила упругости и F – приложенная сила.
Тогда по первому закону Ньютона: [F_{text{упр}}=F] По закону Гука: [F_{text{упр}}=kx] Приравниваем эти формулы: [F=kx] Тогда [k=frac{F}{x}=frac{1500}{0,2}=7500 text{ Н/м}]
Ответ: 7500
К потолку прикреплены одним концом две пружины с одинаковой жесткостью. За другой конец первую пружину растягивают с силой (F_{text{1}}), которая в 2,5 раза больше силы (F_{text{2}}), растягивающей вторую пружину. При этом вторая пружина растянулась на 0,4 м. Насколько растянулась первая пружина? Ответ дать в метрах.
После растяжения обе пружины находятся в покое и на них, кроме данных сил действует сила упругости. Тогда по первому закону Ньютона: [F_{text{упр1}}=F_{text{1}}] [F_{text{упр2}}=F_{text{2}}] где (F_{text{упр1}}) – сила упругости, действующая на первую пружина, (F_{text{упр2}}) – на вторую.
По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [kx_{1}=F_{1}quad(1)] [kx_{2}=F_{text{2}}quad(2)] где (x_{1}) – удлинение первой пружины, (x_{2}) – второй. Разделим (1) на (2), получится: [frac{x_{1}}{x_{2}}=frac{F_{text{1}}}{F_{text{2}}}Rightarrow x_{1}=dfrac{F_{text{1}}x_{2}}{F_{text{2}}}=2,5cdot0,4=1text{ м}]
Ответ: 1
К грузу массой (m) аккуратно подвесили другой груз массой (M), при этом пружина с жесткостью 1200 Н/м удлинилась так, как показано на рисунке. Найдите массу (M). Ускорение свободного падения считать равным 10 м/(c^{2}). Ответ дать в кг.
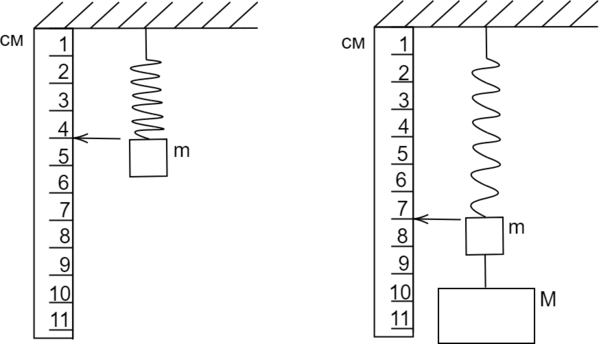
Рассмотрим ситуацию до подвешивания груза: система тел “груз и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg=F_{text{упр}1}] Рассмотрим ситуацию после подвешивания груза: систама тел “2 груза и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg+Mg=F_{text{упр2}}] По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [mg=kx_{1}quad(1)] [mg+Mg=kx_{2}quad(2)] Вычтем (1) из (2), получится: [Mg=k(x_{2}-x_{1})Rightarrow M=dfrac{k(x_{2}-x_{1})}{g}=frac{1200cdot0,03}{10}=3,6text{ кг}]
Ответ: 3,6
Источник
Подробности
Категория: Пружины
Просмотров: 5293
Пружины растяжения навивают почти всегда вплотную или даже с натягом между витками, достигаемым смешением проволокопитателя навивочного автомата по отношению к навиваемым виткам (пружины с межвитковым давлением).
Концы пружин снабжают зацепами, с помощью которых ее соединяют со стягиваемыми деталями. В отличие от пружин сжатия, нуждающихся в жестком направлении торцов, пружины растяжения работают в свободном состояния, центрируясь только точками опоры (завеса). Крепление зацепами обладает шарнирным свойством, благодаря чему пружина может при растяжении менять пространственное положение в значительных пределах. Это делает пружины растяжения особенно удобными для соединения деталей, угловое положение которых изменяется при работе, например, для завеса рычагов (рис. 891, I, II).
Однако крепление зацепами обладает недостатками. Габаритная длина пружины растяжения за счет зацепов всегда больше, чем пружин сжатия одинаковой гибкости. Зацепами трудно обеспечить центральное приложение нагрузки; пружина подвергается дополнительным изгибающим нагрузкам, а в самих зацепах возникают высокие напряжения изгиба, которые могут привести со временем к появлению остаточных деформаций. Вследствие деформации зацепов и участков перехода зацепов в спираль пружина вытягивается и теряет упругие характеристики. Пружины растяжения могут работать без потери упругих свойств только при пониженных расчетных напряжениях.
По этим причинам пружины растяжения почти никогда не применяют в ответственных силовых механизмах (циклического действия). Пружины сжатия в этих условиях обеспечивают и меньшие габариты, и большую надежность работы.
В случаях, когда по условиям работы упругий элемент должен растягиваться с изменением своего пространственного положения, нередко применяют установку пружин сжатия с реверсорами (рис. 892, I, II, III). Пружины такого типа, однако, малопригодны для механизмов высокочастотного циклического действия, так как масса реверсоров вызывает дополнительные инерционные нагрузки.
Применяемые конструкции зацепов показаны на рис. 893. Наиболее простые способы изготовления зацепов — отгибание половины витка (рис. 893, I, II), целого витка (рис. 893, III, IV) или полутора—двух витков (рис. 893, V) — применяют для неответственных, слабонагруженных пружин, так как зацепы такого вида подвержены изгибу. Также подвержены изгибу и петлевые зацепы (рис. 893, VI—VIII), кроме того, их изготовление значительно сложнее. Несколько прочнее зацепы с концами, заведенными в спираль пружины (рис. 893, IX, X).
Легкие пружины из проволоки малого диаметра крепят в пластинках с отверстиями под витки (рис. 893, XI—XIII). В зацепах этого типа необходимо устранить самовыворачивание пружины из отверстий, а также смещение пластинки с плоскости симметрии пружины, что конструктивно не так просто выполнить.
Иногда пружины устанавливают на ввертных резьбовых пробках (рис. 893, XIV—XVI) с фиксацией конечных витков завальцовкой (рис. 893, XV) или расклепыванием ниток пробки (рис. 893, XVI). В конструкциях этого типа крайне неблагоприятны условия работы витка, сходящего с последней нитки резьбовой пробки; виток работает на излом и избежать этого явления невозможно, если даже свести последнюю нитку на нет или заправить резьбу на конус.
Аналогичное явление происходит в конструкции с закладной пробкой, передающей силу на последний виток пружины, свернутый в кольцо малого диаметра (рис. 893, XVII).
Наиболее равномерную передачу сил на витки обеспечивает заправка конечных витков на конус с отгибом последнего витка на зацеп (рис. 893, XVIII, XIX) или с применением закладных зацепов (рис. 893, ХX—XXII). Изготовление таких пружин, однако, затруднительно, особенно при закладных зацепах, когда навивка конусного конца пружины должна производиться при заранее установленном в пружине зацепе.
Из представленных на рис. 893 конструкций наибольшей прочностью отличается конструкция с коническим зацепом (рис. 893, XXXII). Конус зацепа следует (с учетом упругих деформаций конечных витков) делать несколько более пологим, чем внутренний конус витков.
Пружины растяжения рассчитывают по тем же формулам, что и пружины сжатия. Наличие изгибающих напряжений в зацепах и витках пружины (при внецентренном приложении нагрузки) учитывают снижением расчетных напряжений в 1,2—1,5 раза по сравнению с напряжениями, допускаемыми для пружин сжатия центрального нагружения.
На рис. 894 изображена характеристика пружины растяжения. На рис. 895 показана характеристика пружины с начальным натяжением (пружины с межвитковым давлением).
Длина рабочей части пружины растяжения определяется из выражения
где i — число рабочих витков.
Длина рабочей части пружины в растянутом состоянии
где λ — упругое перемещение пружины.
Длина развертки пружины
где α — угол подъема витков
Lз — развернутая длина зацепов. Приближенно можно считать, что
Пружины растяжения обычно устанавливают с предварительным натягом, обеспечивающим замыкание стягиваемых деталей на упор в начальном положении. Сила предварительного натяга определяется условиями работы механизма. Шаг витков в состоянии предварительного натяга делают не меньше 1,5—2 диаметров проволоки с учетом возможности вытяжки зацепов в эксплуатации.
При растяжении диаметр пружины несколько уменьшается вследствие увеличения угла наклона витков.
Источник
