Работа для растяжения пружины
Можно не знать закон Ома и сидеть дома. Но если не знаешь закон Гука – лучше тоже не выходить. Особенно, если идешь на экзамен по физике.
Здесь устраняем пробелы в знаниях и разбираемся, как решать задачи на силу упругости и применение закона Гука. А за полезной рассылкой для студентов добро пожаловать на наш телеграм-канал.
Сила упругости и закон Гука: определения
Сила упругости – сила, препятствующая деформациям и стремящаяся восстановить первоначальные форму и размеры тела.
Примеры действия силы упругости:
- пружины сжимаются и разжимаются в матрасе;
- мокрое белье колышется на натянутой веревке;
- лучник натягивает тетиву, чтобы выпустить стрелу.
Простейшие деформации – деформации растяжения и сжатия.
Закон Гука:
Деформация, возникающая в упругом теле под действием внешней силы, пропорциональна величине этой силы.
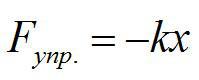
Коэффициент k – жесткость материала.
Есть и другая формулировка закона Гука. Введем понятие относительной деформации «эпсилон» и напряжения материала «сигма»:
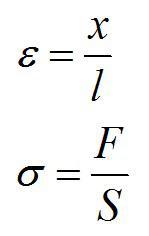
S – площадь поперечного сечения деформируемого тела. Тогда закон Гука запишется так: относительная деформация пропорциональна напряжению.
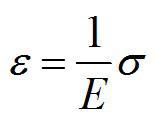
Здесь Е – модуль Юнга, зависящий от свойств материала.
Закон Гука был экспериментально открыт в 1660 году англичанином Робертом Гуком.
Вопросы на силу упругости и закон Гука
Вопрос 1. Какие бывают деформации?
Ответ. Помимо простейших деформаций растяжения и сжатия, бывают сложные деформации кручения и изгиба. Также разделяют обратимые и необратимые деформации.
Вопрос 2. В каких случаях закон Гука справедлив для упругих стержней?
Ответ. Для упругих стержней (в отличие от эластичных тел) закон Гука можно применять при малых деформациях, когда величина эпсилон не превышает 1%. При больших деформациях возникают явления текучести и необратимого разрушения материала.
Вопрос 3. Как направлена сила упругости?
Ответ. Сила упругости направлена в сторону, противоположную направлению перемещения частиц тела при деформации.
Вопрос 4. Какую природу имеет сила упругости?
Ответ. Сила упругости, как и сила трения – электромагнитная сила. Она возникает вследствие взаимодействия между частицами деформируемого тела.
Вопрос 5. От чего зависит коэффициент жесткости k? Модуль Юнга E?
Ответ. Коэффициент жесткости зависит от материала тела, а также его формы и размеров. Модуль Юнга зависит только от свойств материала тела.
Задачи на силу упругости и закон Гука с решениями
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Задача №1. Расчет силы упругости
Условие
Один конец проволоки жестко закреплен. С какой силой нужно тянуть за второй конец, чтобы растянуть проволоку на 5 мм? Жесткость проволоки известна и равна 2*10^6 Н/м2.
Решение
Запишем закон Гука:
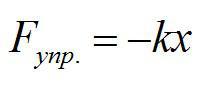
По третьему закону Ньютона:
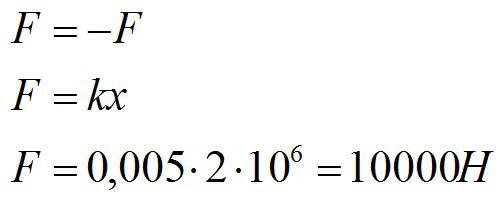
Ответ: 10 кН.
Задача №2. Нахождение жесткости пружины
Условие
Пружину, жесткость которой 100 Н/м, разрезали на две части. Чему равна жесткость каждой пружины?
Решение
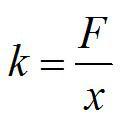
По определению, жесткость обратно-пропорциональна длине. При одинаковой силе F неразрезанная пружина растянется на х, а разрезанная – на x1=x/2.
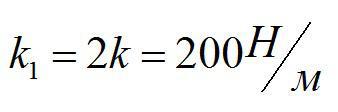
Ответ: 200 Н/м
При растяжении пружины в ее витках возникают сложные деформации кручения и изгиба, однако мы не учитываем их при решении задач.
Задача №3. Нахождение ускорения тела
Условие
Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины, которая при движении растянулась на 2 см. Жесткость пружины 200 Н/м. Определить ускорение, с которым движется тело.
Решение
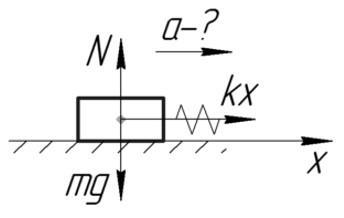
За силу, которая приложена к телу и заставляет его двигаться, можно принять силу упругости. По второму закону Ньютона и по закону Гука:
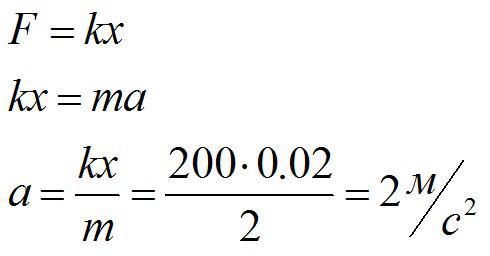
Ответ: 2 м/с^2.
Задача №4. Нахождение жесткости пружины по графику
Условие
На графике изображена зависимость модуля силы упругости от удлинения пружины. Найти жесткость пружины.
Решение

Вспоминаем, что жесткость равна отношению силы и удлинения. Представленная зависимость – линейная. В любой точке прямой отношение ординаты F и абсциссы х дает результат 10 Н/м.
Ответ: k=10 Н/м.
Задача №5. Определение энергии деформации
Условие
Для сжатия пружины на х1=2 см надо приложить силу 10 Н. Определить энергию упругой деформации пружины при сжатии на х2=4 см из недеформированного состояния.
Решение
Энергия сжатой пружины равна:
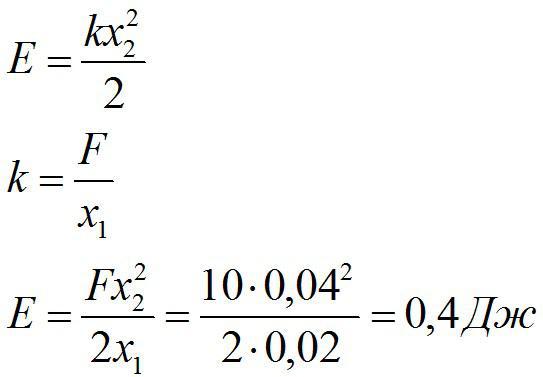
Ответ: 0,4 Дж.
Нужна помощь в решении задач? Обращайтесь за ней в профессиональный студенческий сервис.
Автор
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Источник
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Сила упругости — это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Силы, возникающие при пластических деформациях, не относятся к силам упругости.
Понятие о деформациях
Деформация — это изменение формы и размеров тела.
К деформациям относятся: растяжение, сжатие, кручение, сдвиг, изгиб.
Деформации бывают упругими и пластическими.
Закон Гука
Абсолютная величина силы упругости прямо пропорциональна величине деформации. В частности, для пружины, сжатой или растянутой на величину (displaystyle x) (разница между крайними положениями), сила упругости задается формулой [F=kx] где (displaystyle k) — коэффициент жесткости пружины.
Единицы измерения коэффициента жесткости: (k=)[Н/м].
Закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела.
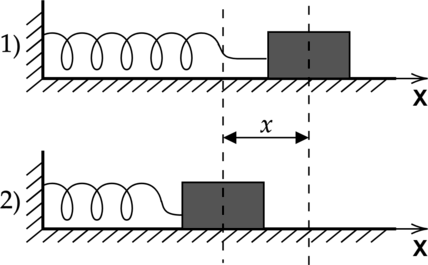
Кубик массой (M = 2) кг, сжатый с боков пружинами, покоится на гладком горизонтальном столе. Первая пружина сжата на 2 см, а вторая сжата на 6 см. Жёсткость первой пружины (k_1 = 1200) Н/м. Чему равна жёсткость второй пружины (k_2)? Ответ выразите в Н/м.
По второму закону Ньютона силы упругости пружин будут уравновешивать друг друга, следовательно: [k_1Delta x_1=k_2Delta x_2] где (Delta x_1) и (Delta x_2) – сжатие первой и второй пружины соответственно.
Откуда жесткость второй пружины [k_2=dfrac{k_1 Delta x_1}{Delta x_2}= dfrac{1200text{ Н/м}cdot 2text{ см}}{6text{ см}}=400text{ Н/м}]
Ответ: 400
На штативе закреплён школьный динамометр. К нему подвесили груз массой 0,1 кг. Пружина динамометра при этом удлинилась на 2,5 см. Чему будет равно удлинение пружины, если масса груза увеличится втрое? (Ответ дайте в сантиметрах)
Согласно закону Гука [F=kDelta x] где k – жесткость пружины, ( Delta x) – удлинение пружины.
Найдем жесткость пружины, зная, что ( Delta x) = 2,5 см = 0,025 м при приложении силы, равно ( F=m_1g=0,1cdot 10=1text{ H} ): [k=dfrac{F}{Delta x}=dfrac{1}{0,025}=40text{ H/кг}] Если массу груза увеличить в 3 раза, то есть, (m_2=0,3) кг, то удлинение пружины будет равно: [Delta x=dfrac{F}{k}=dfrac{m_2g}{k}=dfrac{3cdot0,1cdot10text{ H}}{40text{ H/кг}}=0,075text{ м}=7,5text{ см}]
Ответ: 7,5
К системе из кубика массой M = 3 кг и двух пружин приложена постоянная горизонтальная сила F величиной 20 Н (см. рисунок). Между кубиком и опорой трения нет. Система покоится. Жёсткость первой пружины (k_1 = 400 text{ Н/м}). Жёсткость второй пружины (k_2 = 800 text{ Н/м}). Каково удлинение первой пружины? (Ответ дайте в сантиметрах)
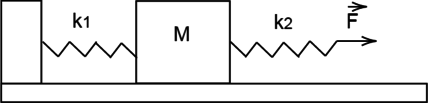
Согласно закону Гука удлинение (Delta x) пружины связано с ее жесткостью k и приложенной к ней силе F выражением (F=kDelta x). На первую пружину действует такая же сила F, что и на вторую, так как трения между кубиком и опорой нет. То, что первая пружина соединена со второй через кубик, здесь не имеет никакого значения, соответственно удлинение первой пружины – это величина, равная: [Delta x=dfrac{F}{k_1}=dfrac{20text{ H}}{400text{ H/м}}=0,05 text{ м}=5 text{ см}]
Ответ: 5
Определите силу, под действием которой пружина жёсткостью 200 Н/см удлинится на 5 мм.
Согласно закону Гука ( F=kDelta x ), где k – жесткость пружины, ( Delta x) – удлинение пружины, получаем: [F=kDelta x=(dfrac{200}{0,01})text{H/м}cdot(5cdot10^{-3})text{м}=100text{ H}]
Ответ: 100
Пружина одним концом прикреплена к неподвижной опоре, к другому концу приложили силу равную 1500 Н, при этом пружина растянулась на 0,2 м. Определите жесткость данной пружины. Ответ дать в Н/м.
После растяжения, пружина покоится и на неё действуют 2 силы направленные в противоположные направления: (F_{text{упр}}) – сила упругости и F – приложенная сила.
Тогда по первому закону Ньютона: [F_{text{упр}}=F] По закону Гука: [F_{text{упр}}=kx] Приравниваем эти формулы: [F=kx] Тогда [k=frac{F}{x}=frac{1500}{0,2}=7500 text{ Н/м}]
Ответ: 7500
К потолку прикреплены одним концом две пружины с одинаковой жесткостью. За другой конец первую пружину растягивают с силой (F_{text{1}}), которая в 2,5 раза больше силы (F_{text{2}}), растягивающей вторую пружину. При этом вторая пружина растянулась на 0,4 м. Насколько растянулась первая пружина? Ответ дать в метрах.
После растяжения обе пружины находятся в покое и на них, кроме данных сил действует сила упругости. Тогда по первому закону Ньютона: [F_{text{упр1}}=F_{text{1}}] [F_{text{упр2}}=F_{text{2}}] где (F_{text{упр1}}) – сила упругости, действующая на первую пружина, (F_{text{упр2}}) – на вторую.
По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [kx_{1}=F_{1}quad(1)] [kx_{2}=F_{text{2}}quad(2)] где (x_{1}) – удлинение первой пружины, (x_{2}) – второй. Разделим (1) на (2), получится: [frac{x_{1}}{x_{2}}=frac{F_{text{1}}}{F_{text{2}}}Rightarrow x_{1}=dfrac{F_{text{1}}x_{2}}{F_{text{2}}}=2,5cdot0,4=1text{ м}]
Ответ: 1
К грузу массой (m) аккуратно подвесили другой груз массой (M), при этом пружина с жесткостью 1200 Н/м удлинилась так, как показано на рисунке. Найдите массу (M). Ускорение свободного падения считать равным 10 м/(c^{2}). Ответ дать в кг.
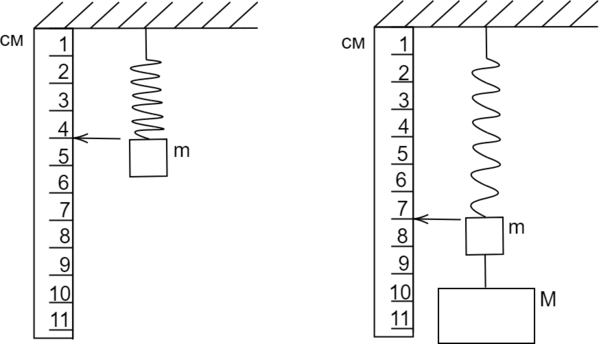
Рассмотрим ситуацию до подвешивания груза: система тел “груз и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg=F_{text{упр}1}] Рассмотрим ситуацию после подвешивания груза: систама тел “2 груза и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg+Mg=F_{text{упр2}}] По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [mg=kx_{1}quad(1)] [mg+Mg=kx_{2}quad(2)] Вычтем (1) из (2), получится: [Mg=k(x_{2}-x_{1})Rightarrow M=dfrac{k(x_{2}-x_{1})}{g}=frac{1200cdot0,03}{10}=3,6text{ кг}]
Ответ: 3,6
Источник
Подробности
Категория: Пружины
Просмотров: 5564
Пружины растяжения навивают почти всегда вплотную или даже с натягом между витками, достигаемым смешением проволокопитателя навивочного автомата по отношению к навиваемым виткам (пружины с межвитковым давлением).
Концы пружин снабжают зацепами, с помощью которых ее соединяют со стягиваемыми деталями. В отличие от пружин сжатия, нуждающихся в жестком направлении торцов, пружины растяжения работают в свободном состояния, центрируясь только точками опоры (завеса). Крепление зацепами обладает шарнирным свойством, благодаря чему пружина может при растяжении менять пространственное положение в значительных пределах. Это делает пружины растяжения особенно удобными для соединения деталей, угловое положение которых изменяется при работе, например, для завеса рычагов (рис. 891, I, II).
Однако крепление зацепами обладает недостатками. Габаритная длина пружины растяжения за счет зацепов всегда больше, чем пружин сжатия одинаковой гибкости. Зацепами трудно обеспечить центральное приложение нагрузки; пружина подвергается дополнительным изгибающим нагрузкам, а в самих зацепах возникают высокие напряжения изгиба, которые могут привести со временем к появлению остаточных деформаций. Вследствие деформации зацепов и участков перехода зацепов в спираль пружина вытягивается и теряет упругие характеристики. Пружины растяжения могут работать без потери упругих свойств только при пониженных расчетных напряжениях.
По этим причинам пружины растяжения почти никогда не применяют в ответственных силовых механизмах (циклического действия). Пружины сжатия в этих условиях обеспечивают и меньшие габариты, и большую надежность работы.
В случаях, когда по условиям работы упругий элемент должен растягиваться с изменением своего пространственного положения, нередко применяют установку пружин сжатия с реверсорами (рис. 892, I, II, III). Пружины такого типа, однако, малопригодны для механизмов высокочастотного циклического действия, так как масса реверсоров вызывает дополнительные инерционные нагрузки.
Применяемые конструкции зацепов показаны на рис. 893. Наиболее простые способы изготовления зацепов — отгибание половины витка (рис. 893, I, II), целого витка (рис. 893, III, IV) или полутора—двух витков (рис. 893, V) — применяют для неответственных, слабонагруженных пружин, так как зацепы такого вида подвержены изгибу. Также подвержены изгибу и петлевые зацепы (рис. 893, VI—VIII), кроме того, их изготовление значительно сложнее. Несколько прочнее зацепы с концами, заведенными в спираль пружины (рис. 893, IX, X).
Легкие пружины из проволоки малого диаметра крепят в пластинках с отверстиями под витки (рис. 893, XI—XIII). В зацепах этого типа необходимо устранить самовыворачивание пружины из отверстий, а также смещение пластинки с плоскости симметрии пружины, что конструктивно не так просто выполнить.
Иногда пружины устанавливают на ввертных резьбовых пробках (рис. 893, XIV—XVI) с фиксацией конечных витков завальцовкой (рис. 893, XV) или расклепыванием ниток пробки (рис. 893, XVI). В конструкциях этого типа крайне неблагоприятны условия работы витка, сходящего с последней нитки резьбовой пробки; виток работает на излом и избежать этого явления невозможно, если даже свести последнюю нитку на нет или заправить резьбу на конус.
Аналогичное явление происходит в конструкции с закладной пробкой, передающей силу на последний виток пружины, свернутый в кольцо малого диаметра (рис. 893, XVII).
Наиболее равномерную передачу сил на витки обеспечивает заправка конечных витков на конус с отгибом последнего витка на зацеп (рис. 893, XVIII, XIX) или с применением закладных зацепов (рис. 893, ХX—XXII). Изготовление таких пружин, однако, затруднительно, особенно при закладных зацепах, когда навивка конусного конца пружины должна производиться при заранее установленном в пружине зацепе.
Из представленных на рис. 893 конструкций наибольшей прочностью отличается конструкция с коническим зацепом (рис. 893, XXXII). Конус зацепа следует (с учетом упругих деформаций конечных витков) делать несколько более пологим, чем внутренний конус витков.
Пружины растяжения рассчитывают по тем же формулам, что и пружины сжатия. Наличие изгибающих напряжений в зацепах и витках пружины (при внецентренном приложении нагрузки) учитывают снижением расчетных напряжений в 1,2—1,5 раза по сравнению с напряжениями, допускаемыми для пружин сжатия центрального нагружения.
На рис. 894 изображена характеристика пружины растяжения. На рис. 895 показана характеристика пружины с начальным натяжением (пружины с межвитковым давлением).
Длина рабочей части пружины растяжения определяется из выражения
где i — число рабочих витков.
Длина рабочей части пружины в растянутом состоянии
где λ — упругое перемещение пружины.
Длина развертки пружины
где α — угол подъема витков
Lз — развернутая длина зацепов. Приближенно можно считать, что
Пружины растяжения обычно устанавливают с предварительным натягом, обеспечивающим замыкание стягиваемых деталей на упор в начальном положении. Сила предварительного натяга определяется условиями работы механизма. Шаг витков в состоянии предварительного натяга делают не меньше 1,5—2 диаметров проволоки с учетом возможности вытяжки зацепов в эксплуатации.
При растяжении диаметр пружины несколько уменьшается вследствие увеличения угла наклона витков.
Источник
Сталин Инопланетянин · 27 июня 2018
4,3 K
Эксперт TQ по темам: IT, телеком, телефония, базы данных, интеграционные…
Пружины бывают разные. Кроме того, непонятно, требуется ли изменить свойства абстрактной пружины (пружины вообще), или нужно изменить работу пружины в уже существующем механизме, не заменяя там эту пружину. Рассмотрим несколько кейсов.
Цилиндрическая витая пружина (абстрактная), работающая на растяжение или сжатие. Чтобы пружина стала жёстче можно: 1) намотать её из более толстой проволоки; 2) намотать меньшее количество витков; 3) использовать сталь с бо̀льшим предельным напряжением кручения; 4) если сталь из которой сделана пружина позволяет, то можно выполнить закалку пружины (нагреть до некой критической температуры и резко охладить)
Цилиндрическая витая пружина в существующем механизме, работающая на растяжение или сжатие. 1) вынуть и закалить пружину, затем поставить на место; 2) заблокировать часть витков пружины (например, если она работает на сжатие, то можно попросту воткнуть что-то твёрдое между несколькими витками); 3) вместе с имеющейся пружиной вставить параллельно еще одну, если механизм это позволяет.
Пластинная пружина (абстрактная), работающая на изгиб (например, пластинчатые автомобильные рессоры). Увеличение жёсткости такой пружины достигается 1) увеличением числа пластин, сложенных вместе; 2) увеличением толщины пластин; 3) изменением формы пластин (вместо увеличения толщины можно согнуть пластину вдоль, создать на ней ребро жёсткости); 3) изменением свойств материала (закалка пластин).
Здравствуйте! Подскажите пожалуйста, как закалить навив. спиральной пружины из ленты 65Г 0,35х3. Спасибо!
Как ослабить пружину?
Для пружины растяжения необходимо добавить количество рабочих витков.
Завод пружин «Фрей» изготавливает пружины сжатия на заказ по чертежам заказчика из пружинной проволоки диаметр от 0.1 до 14 мм с 2008 года.
Как думаете, беспружинные матрасы на пене с высокой плотностью, достойная замена пружинным матрасам?
Пружинные матрасы: основные разновидности и их особенности
Так как пружинные матрасы появились гораздо раньше своих беспружинных аналогов, рассмотрим их в первую очередь. Для начала выделим два основных твида матрасов по типу их пружинного блока:
- зависимый или «боннель» (bonnel).
- независимый или «покет спринг» (pocket spring).
Блок боннель или зависимый пружинный блок
Блок боннель появился довольно давно и известен нам еще с советских времен, с тех самых пресловутых диванов-книжек, внутри которых были установлены именно такие блоки.
Использование настилочных слоев не только влияет на ортопедические качества матраса, но и препятствует прямому контакту металлических элементов с обивочной тканью, защищая ее от преждевременного износа и повреждений
Исходя из конструкции и особенностей данного типа пружинного блока, можно выделить его основные преимущества:
- невысокая цена.
- достаточно неплохие ортопедические качества.
- длительный срок службы (особенно у моделей со вставками из ППУ).
Выбирайте только проверенные матрасы — ОФИЦИАЛЬНЫЙ САЙТ
Все это справедливо при одном условии — производитель соблюдал все стандарты качества и использовал сталь подходящей марки.
Каким бы хорошим блок боннель не был, у него есть и недостатки:
- эффект «волны». Из-за того, что все пружины соединены между собой, колебания от источника нагрузки передаются по всей площади матраса. Особенно это заметно на двуспальных моделях, когда один человек беспокойно спит и часто ворочается во сне — то второй будет также ощущать движение всех пружин под собой. Либо еще один вариант — двое супругов с очень большой разницей в весе. Эффект будет аналогичен. Но для таких случаев есть специальные матрасы, о которых я сделаю отдельный обзор.
- невысокая стойкость к нагрузкам. Плотность посадки пружин на 1м2 небольшая, поэтому при длительной повышенной нагрузке металл начнет терять свои качества. Визуально это будет выглядеть как небольшая яма в центре спального места. Рекомендуемая нагрузка на пружины боннель составляет не более 100 кг на одно место. Некоторые производители используют дополнительные настилочные слои, увеличивающие жесткость, а также укладывают по периметру матраса полосы из ППУ (это так называемый «еврокаркас», который препятствует деформации пружин и всего матраса). Так можно достичь предела нагрузки до 120-130 кг.
- если пружина «просела», то матрас не только теряет свои ортопедические качества, но и начинает издавать характерный металлический скрип, что никак не будет способствовать здоровому сну.
Независимый пружинный блок
Второй представитель пружинных блоков — так называемый pocket spring или независимый блок. Если название bonnel считается общепринятым и универсальным для определения типа зависимого блока, то pocket spring можно встретить не везде. У одних производителей он так и называется, у других — это «покет» или «мультипокет», у третьих — вообще какое-то свое название, поэтому, чтобы не путаться, я буду называть него просто НПБ (независимый пружинный блок).
Выбирайте только проверенные матрасы — ОФИЦИАЛЬНЫЙ САЙТ
Итак, что мы знаем по НПБ?
В основе конструкции блока — все те же пятивитковые пружины, но в отличие от блока боннель, они не связаны между собой общим металлическим каркасом тонкой проволокой или любым другим способом. Ключевая особенность такого блока — каждая пружина находится в своем тряпяничном чехле («стакане»).
Как вы видите, выбор матраса это целое искусство! Но можно и не заморачиваться и выбрать себе тот, который больше всего понравится.
Выбор остаётся за вами!
Прочитать ещё 6 ответов
Какие минусы пружинного блока «змейка» в диванах?
Мебельная мастерская Виконт, более 15 лет опыта в области ремонта мебели, перетяжки… · mmvikont.ru
Из минусов пружин «змейка» в диване можно отметить:
- Короткий эксплуатационный срок
- Не ортопедический эффект
- Плохая амортизация
- Со временем портит наполнитель, прорезает его и крошит в местах соприкосновений
- Могут скрипеть и быстро продавливаться
Из плюсов пружин «змейка» в диване стоит отметить:
- Доступность и распространненность в эконом мебели
- Низкая цена изделия с данными пружинами
- Легкий ремонт, замена
Альтернатива пружинам змейка — ремни эластичные и независимые пружинные блоки
Подписывайтесь на наш профиль, мы приготовили для Вас много полезных ответов и советов в области мебели!
И не забывайте ставить ???? нам будет очень приятно!
Прочитать ещё 2 ответа
Как сделать пружину дома?
Взять мягкую стальную проволоку (или отожженную), скрутить из неё спираль, а потом снова закалить. Получится какая-никакая пружина. В реальности все пружины делаются под конкретную задачу и имеют соответствующие характеристики, а это значит подобраны толщина проволоки, геометрические размеры, качество стали и уровень закалки.
Ну и, конечно, пружины бывают не только спиральные и не только из круглой проволоки.
Если связать сжатую пружину кислотостойкой нитью и растворить пружину в кислоте, то куда денется энергия сжатия?
мои ответы не являются «глубокомысленными» статьями для ЯДзен
В студию приглашается Яков Исидорович Перельман, автор этой задачи:
ЭНЕРГИЯ РАСТВОРЕННОЙ ПРУЖИНЫ
Вы согнули стальную пружину. Затраченная вами работа превратилась в потенциальную энергию -напряженной пружины. Вы можете вновь получить израсходованную энергию, если заставите распрямляющуюся пружину поднимать грузик, вращать колесо и т. п.; часть энергии возвратится в форме полезной работы, часть же уйдет на преодоление вредных сопротивлений (трения). Ни один эрг не пропадет бесследно.
Но вы поступаете с согнутой пружиной иначе: опускаете в серную кислоту, и стальная полоска растворяется. Должник исчез: не с кого взыскать энергию, затраченную на сгибание пружины. Закон сохранения энергии как будто нарушен.
Так ли? Почему собственно мы должны думать, что энергия в этом случае исчезла бесследно? Она могла проявиться в форме кинетической энергии в тот момент, когда пружина, разъеденная кислотой, лопнула, сообщив движение своим частям и окружающей жидкости. Могла она преобразоваться и в теплоту, подняв температуру жидкости. Но ожидать сколько-нибудь заметного повышения температуры не приходится.. В самом деле, пусть края согнутой пружины сближены по сравнению с распрямленной на 10 см (0,1 м). Напряжение пружины примем равным 2 кг; значит, средняя величина силы, сгибавшей пружину, равнялась 1 кг. Отсюда потенциальная энергия пружины равна 1 X 0,1 =0,1 кгм. Это соответствует количеству тепла 2,3 X 0,1 = 0,23 мал. калории. Такое незначительное количество тепла может поднять температуру всего раствора лишь на ничтожную долю градуса, практически неуловимую.
Допустима, однако, возможность перехода энергии согнутой пружины также в электрическую или химическую; в последнем случае это могло бы сказаться ибо ускорением разъедания пружины (если возникшая химическая энергия способствует растворению стали), либо замедлением этого процесса (в обратном случае).
Какая из перечисленных возможностей имеет место на самом деле, может обнаружить только опыт.
Подобный опыт и был произведен (экспериментатор, доктор Гуго Куль, описал его в немецком журнале, «Космос»). Стальная полоска в согнутом положении была зажата между двумя стеклянными палочками, установленными на дне стеклянного сосуда в полусантиметре одна от другой (рис. 70 налево). В другом опыте пружина упиралась прямо в стенки сосуда. В сосуд налили серную кислоту (12 ч. 100/< кислоты в 1 л воды). Полоска вскоре лопнула и обе части были оставлены в кислоте до полного растворения. Продолжительность опыта — от погружения в кислоту пружины до растворения ее частей — была тщательно измерена. Затем опыт растворения был повторен с такой же полоской в несогнутом состоянии, при вполне одинаковых прочих условиях. Оказалось, что растворение ненапряженной полоски потребовало меньше времени.
Это показывает, что напряженная пружина стойче сопротивляется растворению, чем ненапряженная. Значит, несомненно, что энергия, затраченная на сгибание пружины, частью переходит в химическую, частью же — в механическую энергию движущихся частей пружины. Бесследного исчезновения энергии не происходит.
В связи с рассмотренной сейчас задачей я получил несколько писем от читателей, предлагавших мне разъяснить их недоумение по аналогичному поводу. Один задает такую задачу:
«Вязанка дров доставлена на 4-й этаж, отчего запас ее потенциальной энергии увеличился. Куда девается этот избыток потенциальной энергии, когда дрова сгорают?»
Разгадку нетрудно найти, если вспомнить, что после сгорания дров вещество их переходит в продукты горения, которые, образовавшись на известной высоте над землей, обладают большей потенциальной энергией, нежели в том случае, когда они возникают на уровне земной поверхности.
www.booksshare.net
Прочитать ещё 2 ответа
Источник
