Работа деформации при растяжении
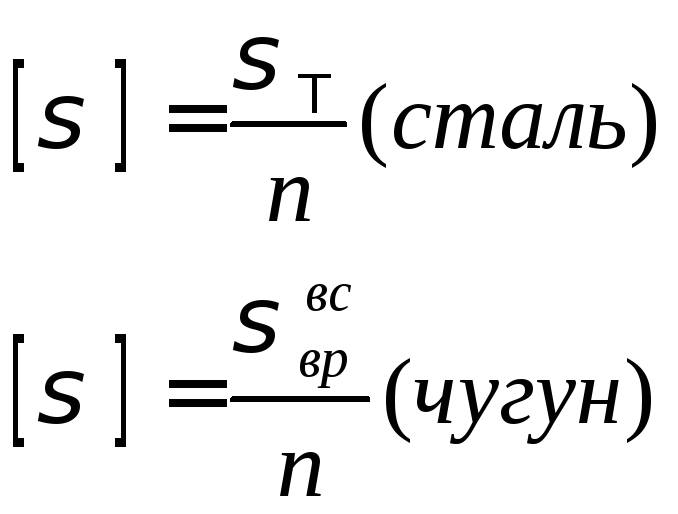
Сопротивление материалов
Деформации при растяжении и сжатии
Продольные деформации при растяжении и сжатии
Характер деформаций, которым подвергается прямой брус при растяжении или сжатии мы определили, проведя опыт с резиновым брусом, на котором была нанесена сетка линий.
Теперь представим себе брус постоянного сечения имеющий длину l, один из концов которого защемлен, а к свободному концу приложена растягивающая сила F. Под действием этой силы брус удлинится на некоторую величину Δl, которую назовем абсолютным удлинением бруса.
Отношение абсолютного удлинения Δl к первоначальной длине бруса l назовем относительным удлинением и обозначим ε:
ε = Δl / l
Относительное удлинение – величина безразмерная, иногда его выражают в процентах.
Итак, деформация бруса при растяжении и сжатии характеризуется абсолютным и относительным удлинением или укорочением.
***
Закон Гука при растяжении и сжатии
Напряжения и деформации при растяжении и сжатии связаны между собой линейной зависимостью, которая называется законом Гука, по имени английского физика Р. Гука (1653-1703 г.г.), установившего этот закон.
Сформулировать закон Гука можно так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению.
Математически эта зависимость записывается так:
σ = E ε.
Здесь Е – коэффициент пропорциональности, который характеризует жесткость материала бруса, т. е. его способность сопротивляться деформации; его называют модулем продольной упругости, или модулем упругости первого рода.
Модуль упругости, как и напряжение, выражаются в паскалях (Па).
Значения Е для различных материалов устанавливаются экспериментально-опытным путем, и их величину можно найти в соответствующих справочниках.
Так, для стали Е = (1,96.…2,16) х 105 МПа, для меди Е = (1,00…1,30) х 105 МПа и т. д.
Следует оговориться, что закон Гука справедлив лишь в определенных пределах нагружения.
Если в формулу закона Гука подставить полученные ранее значения относительного удлинения и напряжения: ε = Δl / l , σ = N / А, то можно получить следующую зависимость:
Δl = Nl / (EА).
Произведение модуля упругости на площадь сечения Е×А, стоящее в знаменателе, называют жесткостью сечения при растяжении и сжатии; оно характеризует одновременно и физико-механические свойства материала бруса и геометрические размеры поперечного сечения этого бруса.
Приведенную выше формулу можно читать так: абсолютное удлинение или укорочение бруса прямо пропорционально продольной силе и длине бруса, и обратно пропорционально жесткости сечения бруса.
Выражение ЕА / l называют жесткостью бруса при растяжении и сжатии.
Приведенные выше формулы закона Гука справедливы лишь для брусьев и их участков, имеющих постоянное поперечное сечение, изготовленных из одного материала и при постоянной силе. Для бруса, имеющего несколько участков, отличающихся материалом, размерами сечения, продольной силой, изменение длины всего бруса определяется, как алгебраическая сумма удлинений или укорочений отдельных участков:
Δl = Σ (Δli)
***
Поперечные деформации при растяжении и сжатии
Описанный ранее опыт с резиновым брусом, на котором нанесена сетка линий, показал, что при растяжении поперечные размеры бруса уменьшаются, а при сжатии – увеличиваются, т. е. брус становится либо тоньше, либо толще. Это явление характерно для брусьев, изготовленных из всех материалов.
Опытным путем установлено, что при одноосном растяжении или сжатии отношение относительных поперечной и продольной деформаций для данного материала – величина постоянная.
Впервые на эту зависимость указал французский ученый С. Пуассон (1781-1840 г.г.) и математически она записывается так:
|ε1| = ν |ε|,
где ν – коэффициент поперечной деформации, называемый коэффициентом Пуассона.
Коэффициент Пуассона является безразмерной величиной, и характеризует упругие свойства материала. При растяжении и сжатии этот коэффициент принимается одинаковым.
Значения коэффициента Пуассона для разных материалов установлены опытным путем и их величины можно найти в соответствующих справочниках.
***
Потенциальная энергия деформации при растяжении
При статическом (медленном) растяжении образца растягивающая сила F возрастает от нуля до какого-то значения, удлиняет образец на величину Δl и при этом совершает работу W.
Эта работа аккумулируется в деформируемом образце в виде потенциальной энергии деформации U, причем, пренебрегая незначительными потерями энергии (например, тепловыми), можно считать, что W = U.
Путем изучения диаграмм растяжения образцов, установлено, что потенциальная энергия упругой деформации стержня длиной l постоянного поперечного сечения А при одинаковой во всех сечениях продольной силе N = F будет равна:
U = W = F Δl / 2 = N2 l / (2E А)
Сопротивление материалов оперирует, также, таким понятием, как удельная потенциальная энергия деформации, которая подсчитывается, как потенциальная энергия, приходящаяся на единицу объема бруса.
При одновременном действии растягивающих и сжимающих нагрузок или ступенчатом изменении размеров поперечного сечения бруса, его разбивают на однородные участки и для каждого подсчитывают потенциальную энергию деформации. Потенциальную энергию деформации всего бруса определяют, как сумму потенциальных энергий отдельных участков.
Анализируя формулу потенциальной энергии деформации можно сделать вывод, что эта величина всегда положительная, поскольку в ее выражения входят квадраты линейных и силовых величин. По этой причине при вычислении потенциальной энергии деформации нельзя применять принцип независимости действия сил (поскольку квадрат суммы не равен сумме квадратов слагаемых).
Единицей измерения потенциальной энергии деформации, как и работы, является джоуль (Дж).
***
Материалы раздела «Растяжение и сжатие»:
- Основные понятия о деформации растяжения и сжатия.
- Расчеты на прочность при растяжении и сжатии. Статически неопределимые задачи.
Смятие
Правильные ответы на вопросы Теста № 5
№ вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Правильный вариант ответа | 3 | 3 | 1 | 2 | 1 | 3 | 2 | 2 | 1 | 1 |
Источник
Внутренние усилия при растяжении-сжатии.
Осевое (центральное) растяжение или сжатие прямого бруса вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса. При растяжении или сжатии в поперечных сечениях бруса возникают только продольные силы N. Продольная сила N в некотором сечении равна алгебраической сумме проекции на ось стержня всех внешних сил, действующих по одну сторону от рассматриваемого сечения. По правилу знаков продольной силы N принято считать, что от растягивающих внешних нагрузок возникают положительные продольные силы N, а от сжимающих — продольные силы N отрицательны (рис. 5).

Чтобы выявить участки стержня или его сечения, где продольная сила имеет наибольшее значение, строят эпюру продольных сил, применяя метод сечений, подробно рассмотренный в статье:
Анализ внутренних силовых факторов в статистически определимых системах
Ещё настоятельно рекомендую взглянуть на статью:
Расчёт статистически определимого бруса
Если разберёте теорию в данной статье и задачи по ссылкам, то станете гуру в теме «Растяжение-сжатие» =)
Напряжения при растяжении-сжатии.
Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:
где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.
Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:
Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.
Деформации при растяжении-сжатии.
Рассмотрим деформации, возникающие при растяжении (сжатии) стержня (рис.6, а). Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l1 и его длины до деформации l
Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением, или относительной продольной деформацией:
При растяжении продольная деформация положительна, а при сжатии – отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:
где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).
Таблица 1
Модуль продольной упругости для различных материалов

Абсолютная поперечная деформация бруса равна разности размеров поперечного сечения после и до деформации:
Соответственно, относительную поперечную деформацию определяют по формуле:
При растяжении размеры поперечного сечения бруса уменьшаются, и ε’ имеет отрицательное значение. Опытом установлено, что в пределах действия закона Гука при растяжении бруса поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε’ к продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона μ:
Экспериментально установлено, что на упругой стадии нагружения любого материала значение μ = const и для различных материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5 (табл. 2).
Таблица 2
Коэффициент Пуассона.

Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N:
Данной формулой можно пользоваться для вычисления абсолютного удлинения участка стержня длиной l при условии, что в пределах этого участка значение продольной силы постоянно. В случае, когда продольная сила N изменяется в пределах участка стержня, Δl определяют интегрированием в пределах этого участка:
Произведение (Е·А) называют жесткостью сечения стержня при растяжении (сжатии).
Механические свойства материалов.
Основными механическими свойствами материалов при их деформации являются прочность, пластичность, хрупкость, упругость и твердость.
Прочность — способность материала сопротивляться воздействию внешних сил, не разрушаясь и без появления остаточных деформаций.
Пластичность – свойство материала выдерживать без разрушения большие остаточные деформации. Неисчезающие после снятия внешних нагрузок деформации называются пластическими.
Хрупкость – свойство материала разрушаться при очень малых остаточных деформациях (например, чугун, бетон, стекло).
Идеальная упругость – свойство материала (тела) полностью восстанавливать свою форму и размеры после устранения причин, вызвавших деформацию.
Твердость – свойство материала сопротивляться проникновению в него других тел.
Рассмотрим диаграмму растяжения стержня из малоуглеродистой стали. Пусть круглый стержень длинной l0 и начальным постоянным поперечным сечением площади A0 статически растягивается с обоих торцов силой F.

Диаграмма сжатия стержня имеет вид (рис. 10, а)

где Δl = l — l0 абсолютное удлинение стержня; ε = Δl / l0 — относительное продольное удлинение стержня; σ = F / A0 — нормальное напряжение; E — модуль Юнга; σп — предел пропорциональности; σуп — предел упругости; σт — предел текучести; σв — предел прочности (временное сопротивление); εост — остаточная деформация после снятия внешних нагрузок. Для материалов, не имеющих ярко выраженную площадку текучести, вводят условный предел текучести σ0,2 — напряжение, при котором достигается 0,2% остаточной деформации. При достижении предела прочности в центре стержня возникает локальное утончение его диаметра («шейка»). Дальнейшее абсолютное удлинение стержня идет в зоне шейки ( зона местной текучести). При достижении напряжением предела текучести σт глянцевая поверхность стержня становится немного матовой – на его поверхности появляются микротрещины (линии Людерса-Чернова), направленные под углом 45° к оси стержня.

Расчеты на прочность и жесткость при растяжении и сжатии.
Опасным сечением при растяжении и сжатии называется поперечное сечение бруса, в котором возникает максимальное нормальное напряжение. Допускаемые напряжения вычисляются по формуле:
где σпред — предельное напряжение (σпред = σт — для пластических материалов и σпред = σв — для хрупких материалов); [n] — коэффициент запаса прочности. Для пластических материалов [n] = [nт] = 1,2 … 2,5; для хрупких материалов [n] = [nв] = 2 … 5, а для древесины [n] = 8 ÷ 12.
Расчеты на прочность при растяжении и сжатии.
Целью расчета любой конструкции является использование полученных результатов для оценки пригодности этой конструкции к эксплуатации при минимальном расходе материала, что находит отражение в методах расчета на прочность и жесткость.
Условие прочности стержня при его растяжении (сжатии):
При проектном расчете определяется площадь опасного сечения стержня:
При определении допускаемой нагрузки рассчитывается допускаемая нормальная сила:
Расчет на жесткость при растяжении и сжатии.
Работоспособность стержня определяется его предельной деформацией [ l ]. Абсолютное удлинение стержня должно удовлетворять условию:
Часто дополнительно делают расчет на жесткость отдельных участков стержня.
Следующая важная статья теории:
Изгиб балки
Источник
Возьмем диаграмму растяжения в координатах
РиΔlи
посмотрим, что выражает собой вся площадь
диаграммы ОАВDЕ (рис.8).
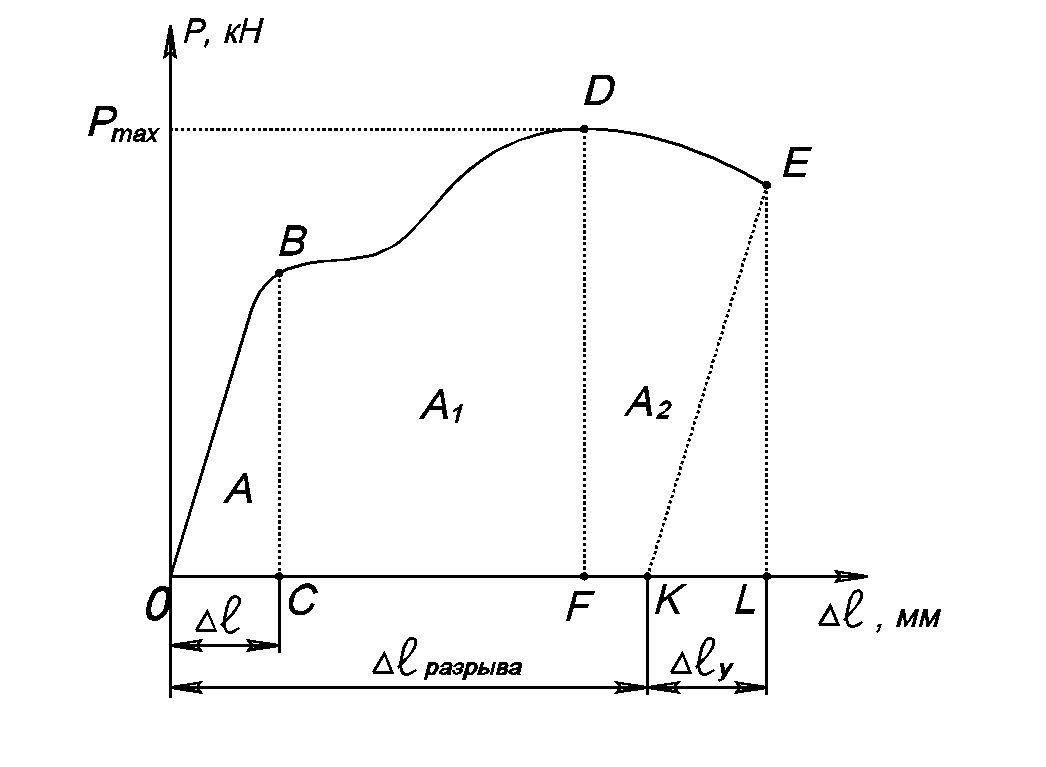
Рис.8.
Диаграмма растяжения (в абсолютных
единицах).
По оси абсцисс отложены полные удлинения
образца, иначе, пути, пройденные точкой
приложения растягивающих сил, а на оси
ординат – величины этих сил. Площадь
всей диаграммы очевидно выражает собой
работу внешних растягивающих сил,
затраченную на разрыв образца.
Вся работа деформации может быть
разделена на три части.
Площадь диаграммы ОВС представляет
собой работу упругой деформации, которая
накапливается в материале в виде
потенциальной энергии и может быть
полностью возвращена материалом, если
снять нагрузку, и равна площади ΔОВС.
![]()
По этой формуле можно вычислять работу
деформации для любой точки диаграммы
до предела упругости.
Вторая часть диаграммы – от предела
упругости до предела прочности – площадь
СВDF– представляет собой
работу А1, затрачиваемую
преимущественно на образование остаточной
деформации.
А1= площади СВDF–
работа, затрачиваемая на образование
остаточной деформации.
Третья часть диаграммы – от предела
прочности до напряжения, при котором
происходит разрыв образца, т.е. площадь
FDЕК. Представляет собой
работу А2, затрачиваемую на разрыв
образца после образования в нем шейки.
А2= площадиFDЕК –
работа, затрачиваемая на разрыв образца
после образования шейки.
Аразр= А+А1+А2– вся
работа деформации до полного разрушения.
![]()
1.4. Работа силы при удлинении наΔl.
Определим работу, которую выполняет
сила Р при удлинении стержня на Δl.
В процессе растяжения стержня сила
меняется линейно от нуля до максимального
значения.
![]()
Элементарная работа силы равна
![]()
Работа силы равна
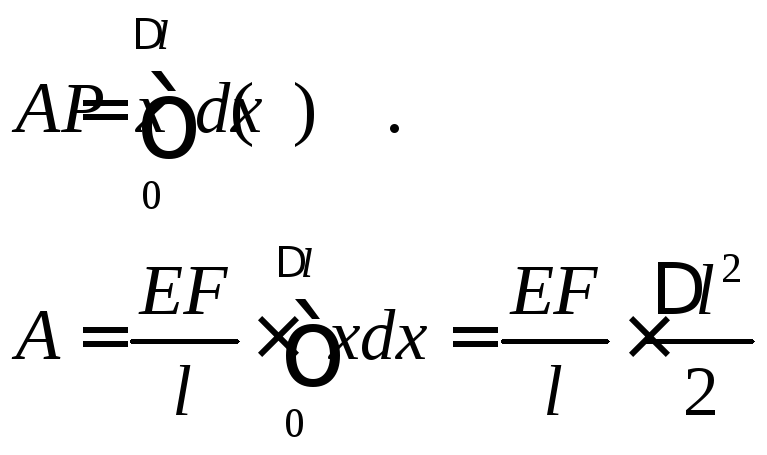
![]() ,
,
следовательно
![]()
1.5. Испытание на сжатие (сталь, чугун, дерево, цемент).
Как показал опыт, результаты, получающиеся
при испытании стали на растяжение и
сжатие равноценны.
Характерные точки диаграммы растяжения
(А, В, С, D,) будут повторяться
(см. рис.5). После точки D кривая пойдет
вверх. Пластичные материалы при испытании
на сжатие не разрушаются, но изменяют
первоначальную форму и размеры (от
цилиндрической к бочкообразной).
Результаты испытаний чугуна на растяжение
и сжатие неравноценны. Опыт показал,
что хрупкие материалы гораздо лучше
работают на сжатие, чем на растяжение.
Разрушение происходит под углом 45°,
т.к. чугун разрушается от максимальных
касательных напряжений.
![]() ,
,
так как![]()
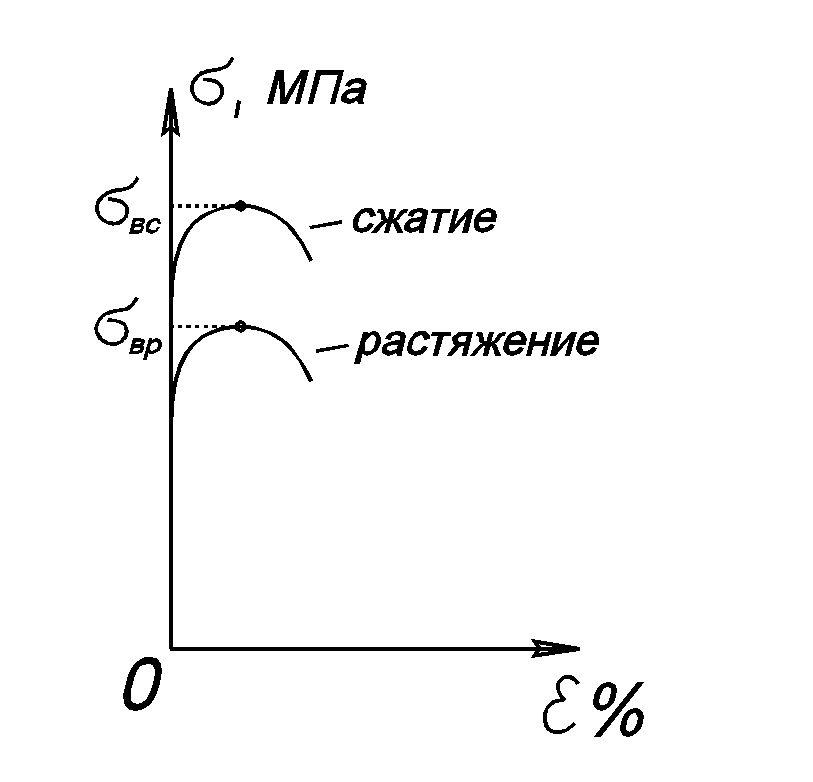
Рис.9.
Диаграмма сжатия и растяжения для
чугуна.
![]()
![]() — верхнее значение напряжения при
— верхнее значение напряжения при
растяжении,
![]() — верхнее значение напряжения при сжатии.
— верхнее значение напряжения при сжатии.
Образцы для испытания на сжатие дерева
и цемента имеют кубическую форму. Дерево
– материал анизотропный, т.к. его
физико-механические свойства различны
по направлениям. Дерево сжимают вдоль
волокон и поперек волокон. Вдоль волокон
дерево выдерживает большие нагрузки и
лучше работает на сжатие, чем поперек
волокон. Форма, которую приобретает
образец после испытаний зависит от
материала, от отношения его высоты к
размерам поперечного сечения и, главным
образом, от трения, возникающего в
полостях соприкосновения оснований
образцов с плитами пресса. Большое
трение по торцам образца ведет к
неравномерному распределению напряжений
в плоскостях поперечных сечений, что
нежелательно, поэтому это трение
необходимо уменьшать (шлифовка, смазка
оснований парафином).
Лекция № 5
Напряжения максимальные, опасные,
допустимые.
Правила построения эпюр на
растяжение-сжатие.
Напряжения бывают:
Максимаьные
![]() -наибольшие
-наибольшие
напряжения возникающие в конструкции
Опасные![]() -минимальные
-минимальные
напряжения при которых появляются
значительные остаточные деформации.
Для стали предел текучести, для чугуна
верхнее значение при растяжении и
верхнее значение при сжатии.
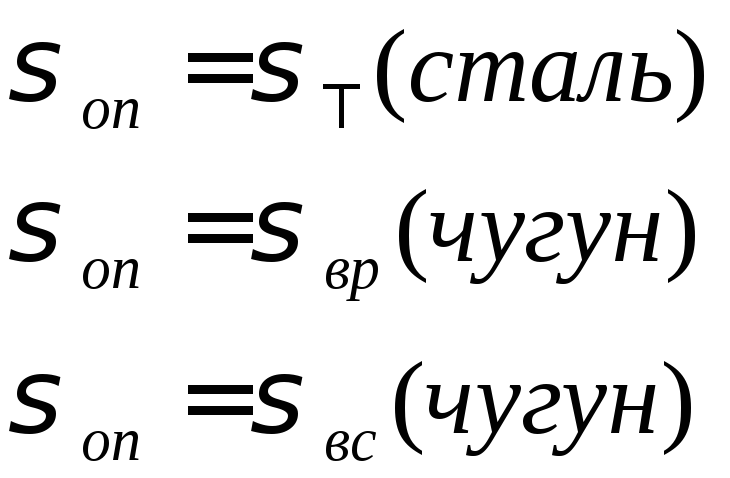
Допустимые
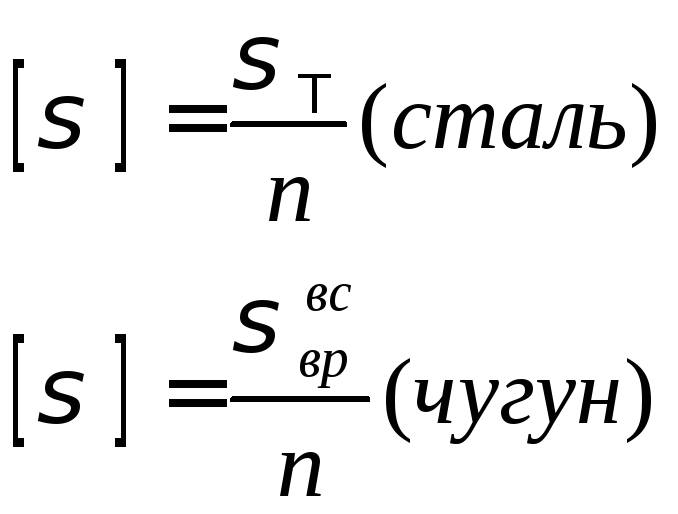
Где
![]() —
—
коэффициент запаса прочности зависит
от материала и от степени ответственности
детали в конструкции.
Условие прочности первый тип расчёта
на прочность — проверочный:
1.
![]() -максимальные
-максимальные
напряжения меньше или равны допустимым
– проверочный расчёт на прочность. Если
данное условие не выполняется необходимо
пересчитать площадь сечения, это второй
тип расчёта – проектный:
2.
![]()
Правила построения эпюр на
растяжение-сжатие.
1. На рисунке проводиться ось ОХ,
совпадающая с продольной осью стержня.
2. Под рисунком стержня проводятся две
базовые нулевые линии, параллельно
продольной оси стержня. Одна для эпюры
продольной силы Nz
Вторая базовая нулевая линия для эпюры
нормальных напряжений![]() (Мпа).
(Мпа).
3. Стержень разбивается на участки. Для
границ участков проводятся вертикальные
линии в точках приложения нагрузки и
изменения площади поперечного сечения
вниз до пересечения с базовыми нулевыми
линиями. Нумерация участков начинается
со свободной стороны стержня для задачи
статически определимой. Если задача
статически неопределимая, то нумерация
выполняется слева направо.
4. Для определения значения продольной
силы используется метод сечений. В
середине участка проводится сечение.
Указывается направление продольной
силы. Положительным считается направление
продольной силы, направленной от сечения
(растягивает). Значение продольной силы
Nzопределяется из условия равновесия
отсечённой части (сумма проекций на ось
ох всех действующих сил равна нулю 0).
5. Вычисляем значение нормальных
напряжений.
6. Положительные значения продольной
силы и нормального напряжения откладываем
вверх от базовой нулевой линии,
отрицательные вниз.
7. Проверяем правильность решения задачи
по эпюре продольной силы. В точках, где
приложена сосредоточенная сила, на
эпюре должен быть скачок равный значению
продольной силы.
8. Условие прочности
![]() проверяем по эпюре нормальных напряжений.
проверяем по эпюре нормальных напряжений.
Максимальные напряжения, возникающие
в конструкции, не должны превышать
допускаемых.
Пример №1: Построить эпюры продольной
силыNи
нормального напряженияσ,проверить на прочность стальной стержень,
закрепленный с одной стороны (статически
определимая задача). Р1
=10кН Р2
=15кН
Р3 =15кН
![]() =100
=100
Мпа; А1 =F;
А2 =2F; F=100мм2
Решение:
Параллельно продольной оси стержня
проводим две базовые нулевые линии для
продольной силы и нормального напряжения.
Разбиваем стержень на участки, начиная
со свободной стороны. Проводим вниз
вертикальные линии в точках приложения
сил и изменения площади поперечного
сечения до пересечения с нулевыми
линиями. Нумерация участков начинается
со свободной стороны стержня.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
