Примеры растяжения в физике

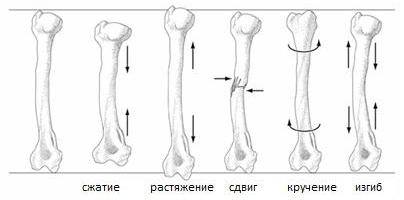
Деформация сдвига, кручения, изгиба – это изменение объема и формы тела при воздействии на него дополнительной нагрузки. При этом меняются расстояния между молекулами или атомами, приводящие к появлению сил упругости. Рассмотрим основные виды деформаций и их характеристики.

Сжатие и растяжение
Деформация растяжения связана с относительным либо абсолютным удлинением тела. В качестве примера можно привести однородный стержень, который закреплен с одного конца. При приложении вдоль оси силы, действующей в противоположном направлении, наблюдается растягивание стержня.
Сила же, прикладываемая по направлению к закрепленному концу стержня, приводит к сжатию тела. В процессе сжатия либо растяжения происходит изменение площади сечения тела.
Деформация растяжения – это изменения состояния объекта, сопровождающиеся смещением его слоев. Данный вид можно проанализировать на модели твердого тела, состоящего из параллельных пластин, которые между собой соединены пружинками. За счет горизонтальной силы осуществляется сдвиг пластин на какой-то угол, объем тела при этом не меняется. В случае упругих деформаций между силой, приложенной к телу, и углом сдвига выявлена прямо пропорциональная зависимость.
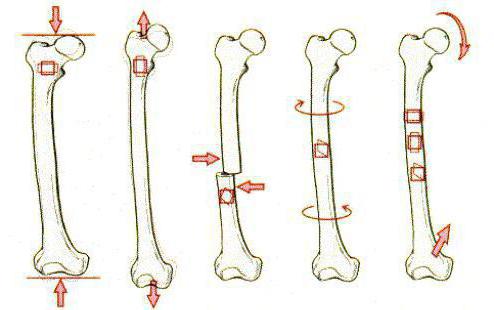
Деформация изгиба
Рассмотрим примеры деформации данного вида. В случае изгиба, выпуклая часть тела подвергается некоторому растяжению, а вогнутый фрагмент сжимается. Внутри тела, подвергающегося данному варианту деформации, есть слой, который не испытывает ни сжатия, ни растяжения. Его принято называть нейтральным участком деформируемого тела. Вблизи него можно уменьшить площадь тела.
В технике примеры деформации данного типа используют для экономии материалов, а также для уменьшения веса возводимых конструкций. Сплошные брусья и стержни заменяют трубами, рельсами, двутавровыми балками.
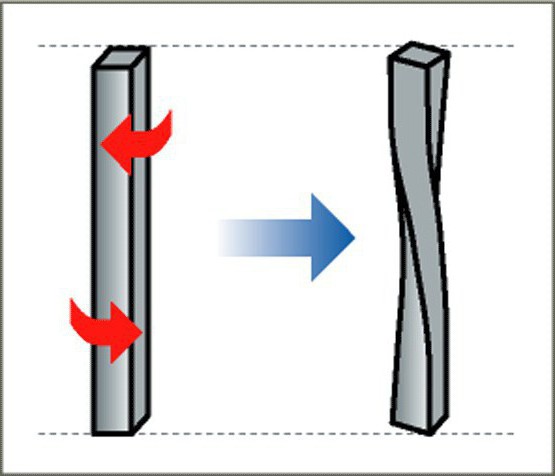
Деформация кручения
Эта продольная деформация является неоднородным сдвигом. Она возникает при действии сил, направленных параллельно либо противоположно на стержень, у которого закреплен один конец. Чаще всего сложным деформациям подвергаются различные детали и механизмы, применяемые в конструкциях и машинах. Но благодаря сочетанию нескольких вариантов деформаций, существенно облегчается вычисление их свойств.
Кстати, в процессе существенной эволюции кости птиц и животных приняли трубчатый вариант строения. Такое изменение способствовало максимальному упрочнению скелета при определенной массе тела.
Деформации на примере организма человека
Тело человека подвергается серьезным механическим нагрузкам от собственных усилий и веса, появляющихся по мере физической деятельности. Вообще, деформация (сдвиг) характерна для человеческого организма:
- Сжатие испытывает позвоночник, покровы ступней, нижние конечности.
- Растяжению подвергаются связки, верхние конечности, мышцы, сухожилья.
- Изгиб характерен для конечностей, костей таза, позвонков.
- Кручениям подвергается во время поворота шея, при вращении ее испытывают кисти рук.
Но при превышении показателей предельного напряжения, возможен разрыв, например костей плеча, бедра. В связках же ткани соединяются настолько эластично, что допускается растягивание их в два раза. Кстати, деформация сдвига объясняет всю опасность передвижения женщин на высоких каблуках. Вес тела будет переноситься на пальцы, что приведет к повышению нагрузки на кости в два раза.
По результатам медицинских осмотров, проводимых в школах, из десяти детей лишь одного можно считать здоровым. Как деформации связаны с детским здоровьем? Сдвиг, кручение, сжатие – основные причины нарушения осанки у детей и подростков.
Прочность и деформации
Несмотря на многообразие живого и неживого мира, на создание человеком многочисленных материальных объектов, у всех предметов и живых существ есть общее свойство — прочность. Под ней принято понимать способность материала сохраняться на протяжении длительного временного промежутка без видимых разрушений. Существует прочность конструкций, молекул, сооружений. Эта характеристика уместна для кровеносных сосудов, человеческих костей, кирпичной колонны, стекла, воды. Деформация сдвига – вариант проверки сооружения на прочность.
Применение разных видов деформаций человеком имеет глубокие исторические корни. Все начиналось с желания соединить между собой палку и острый наконечник, чтобы охотиться на древних животных. Уже в те далекие времена человека интересовала деформация. Сдвиг, сжатие, растяжение, изгиб помогали ему создавать жилища, орудия труда, готовить пищу. По мере развития техники человечеству удалось использовать различные виды деформаций так, чтобы они приносили весомую пользу.
Закон Гука
Математические расчеты, необходимые в строительстве, технике, позволили применять закон Гука для деформации сдвига. Формула показывала прямую связь между силой, прикладываемой к телу, и его удлинением (сжатием). Гук использовал коэффициент жесткости, показывая связь между материалом и возможностью его деформации.
По мере развития и совершенствования технических средств, аппаратов и приборов, разработки теории сопротивления, были проведены серьезные исследования пластичности и упругости. Результаты проведенных фундаментальных экспериментов стали применять в строительной технике, теории сооружений, теоретической механике.
Благодаря комплексному подходу к проблемам, связанным с различными видами деформации, удалось развить строительную отрасль, осуществлять профилактику правильной осанки у подрастающего поколения страны.
Заключение
Деформации, рассматриваемые в курсе школьной физики, оказывают влияние на процессы, происходящие в живом мире. В организмах человека, животных постоянно происходит кручение, изгиб, растяжение, сжатие. И для того чтобы осуществлять своевременную и полноценную профилактику проблем, связанных с осанкой или избыточным весом, медики используют зависимости, выявленные физиками при проведении фундаментальных исследований.
Например, прежде чем осуществлять протезирование нижних конечностей, выполняется детальный расчет максимальной нагрузки, на которую он должен быть рассчитан. Протезы подбираются для каждого человека индивидуально, так как важно учесть вес, рост и подвижность последнего. При нарушениях осанки применяют специальные коррекционные пояса, основанные на использовании деформации сдвига. Современная реабилитационная медицина не смогла бы существовать без использования физических законов и явлений, в том числе и без учета закономерностей различных видов деформаций.
Источник
Деформация растяжения — вид деформации, при которой нагрузка прикладывается продольно от тела, то есть соосно или параллельно точкам крепления тела. Проще всего растяжение рассмотреть на буксировочном тросе для автомобилей. Трос имеет две точки крепления к буксиру и буксируемому объекту, по мере начала движения трос выпрямляется и начинает тянуть буксируемый объект. В натянутом состоянии трос подвергается деформации растяжения, если нагрузка меньше предельных значений, которые может он выдержать, то после снятия нагрузки трос восстановит свою форму.
Деформация растяжения является одним из основных лабораторных исследований физических свойств материалов. В ходе приложения растягивающих напряжений определяются величины, при которых материал способен:
1. воспринимать нагрузки с дальнейшим восстановлением первоначального состояния (упругая деформация)
2. воспринимать нагрузки без восстановления первоначального состояния (пластическая деформация)
3. разрушаться на пределе прочности
Данные испытания являются главными для всех тросов и веревок, которые используются для строповки, крепления грузов, альпинизма. Растяжение имеет значение также при строительстве сложных подвесных систем со свободными рабочими элементами.
Деформация сжатия
Деформация сжатия — вид деформации, аналогичный растяжению, с одним отличием в способе приложения нагрузки, ее прикладывают соосно, но по направлению к телу. Сдавливание объекта с двух сторон приводит к уменьшению его длины и одновременному упрочнению, приложение больших нагрузок образовывает в теле материала утолщения типа «бочка».
Деформация сжатия широко используется в металлургических процессах ковки металла, в ходе процесса металл получает повышенную прочность и заваривает дефекты структуры. Сжатие также важно при строительстве зданий, все элементы конструкции фундамента, свай и стен испытывают давящие нагрузки. Правильный расчет несущих конструкций здания позволяет сократить расход материалов без потери прочности.
Деформация сдвига
Деформация сдвига — вид деформации, при котором нагрузка прикладывается параллельно основанию тела. В ходе деформации сдвига одна плоскость тела смещается в пространстве относительно другой. На предельные нагрузки сдвига испытываются все крепежные элементы — болты, шурупы, гвозди. Простейший пример деформации сдвига – расшатанный стул, где за основание можно принять пол, а за плоскость приложения нагрузки – сидение.
Деформация изгиба
Деформация изгиба — вид деформации, при котором нарушается прямолинейность главной оси тела. Деформации изгиба испытывают все тела подвешенные на одной или нескольких опорах. Каждый материал способен воспринимать определенный уровень нагрузки, твердые тела в большинстве случаев способны выдерживать не только свой вес, но и заданную нагрузку. В зависимости от способа приложения нагрузки при изгибе различают чистый и косой изгиб.
Значение деформации изгиба важно для проектирования упругих тел, таких, как мост с опорами, гимнастический брус, турник, ось автомобиля и другие.
Деформация кручения
Деформация кручения – вид деформации, при котором к телу приложен крутящий момент, вызванный парой сил, действующих в перпендикулярной плоскости оси тела. На кручение работают валы машин, шнеки буровых установок и пружины.
Зако́н Гу́ка — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Открыт в 1660 году английским учёным Робертом Гуком. Поскольку закон Гука записывается для малых напряжений и деформаций, он имеет вид простой пропорциональности.
В словесной форме закон звучит следующим образом:
Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации
Для тонкого растяжимого стержня закон Гука имеет вид:
Здесь — сила, которой растягивают (сжимают) стержень, — абсолютное удлинение (сжатие) стержня, а — коэффициент упругости (или жёсткости).
Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения и длины ) явно, записав коэффициент упругости как
Величина называется модулем упругости первого рода или модулем Юнга и является механической характеристикой материала.
Если ввести относительное удлинение
и нормальное напряжение в поперечном сечении
то закон Гука в относительных единицах запишется как
В такой форме он справедлив для любых малых объёмов материала.
Также при расчёте прямых стержней применяют запись закона Гука в относительной форме
Модуль Юнга (модуль упругости) — физическая величина, характеризующая свойства материала сопротивляться растяжению/сжатию при упругой деформации[1]. Назван в честь английского физика XIX века Томаса Юнга. В динамических задачах механики модуль Юнга рассматривается в более общем смысле — как функционал среды и процесса. В Международной системе единиц (СИ) измеряется в ньютонах на метр в квадрате или в паскалях.
Модуль Юнга рассчитывается следующим образом:
где:
· E — модуль упругости,
· F — сила,
· S — площадь поверхности, по которой распределено действие силы,
· l — длина деформируемого стержня,
· x — модуль изменения длины стержня в результате упругой деформации (измеренного в тех же единицах, что и длина l).
Через модуль Юнга вычисляется скорость распространения продольной волны в тонком стержне:
где — плотность вещества.
Электричество
Источник
Упругие деформации, возникающие в телах, могут быть весьма разнообразны. Тело может растягиваться или сжиматься, изгибаться, перекашиваться, скручиваться. В большинстве случаев наблюдаемая деформация представляет собой несколько деформаций одновременно. В конечном счете, однако, любую деформацию можно свести к двум наиболее простым: растяжению (или сжатию) и сдвигу.
Стальная струна на балалайке, простая (не витая) проволока, поддерживающая груз, резиновая нить в рогатке служат примерами тел, подвергнутых одностороннему растяжению, ибо тело растягивается вдоль одного только направления. При таком растяжении тела удлиняются и одновременно несколько уменьшаются в поперечных размерах. Это хорошо видно при растяжении резиновой полоски, на которой начерчена сетка линий (рис. 459). Вследствие растяжения тела находятся в напряженном состоянии. В примере с резиновой полоской деформация отдельных частей ее, а следовательно, и напряжение приблизительно одинаковы по всему ее объему, за исключением мест вблизи приложения внешних сил. То же можно сказать и относительно натянутой струны.

Рис. 459. а) На резиновой полоске начерчена сетка, ячейки которой имеют форму квадратов, б) При растяжении полоски ячейки сетки превращаются в прямоугольники
Бревна, распирающие грунт в глубоких узких канавах (рис. 460) или в рудниках, колонны, на которых покоится часть здания, ножки стола, поддерживающие столешницу, являются примерами тел, подвергнутых сжатию. Здесь мы имеем примеры одностороннего сжатия. При одностороннем сжатии тело немного «раздается», т. е. увеличивается в поперечных направлениях. Это хорошо заметно, если сжимать мягкую резинку, на которой начерчена сетка линий (рис. 461). На этом рисунке заметно также, что деформации отдельных частей могут быть неодинаковыми в разных местах тела: в середине резинка деформирована больше, чем по краям.

Рис. 460. Бревна
, удерживающие грунт от осыпания, находятся в состоянии сжатия

Рис. 461. Сжатие резинки. Ячейки сетки более деформированы в середине, чем по краям
Измеряя растяжение проволок или сжатие стержней из различных материалов под действием данной нагрузки, мы обнаружим, что деформация тем больше, чем длиннее образец и чем меньше его поперечное сечение. Это нетрудно понять. Чем толще образец, тем меньшая нагрузка приходится на единицу площади его сечения, а чем он длиннее, тем больше будет удлинение, которое составляет определенную часть первоначальной длины: каждая единица длины получает одно и то же приращение. Свойства материала сказываются очень сильно. Например, стальная проволока при тех же размерах и нагрузке растягивается в два с лишним раза меньше, чем медная.
При рассмотренных односторонних деформациях тела находятся под действием двух равных по модулю, противоположно направленных сил.
Нередко в природе и в технике мы встречаемся со всесторонними деформациями: всесторонним сжатием и всесторонним растяжением. И та и другая деформации наблюдаются в том случае, если деформируемое тело подвергается давлению со всех сторон или растяжению во все стороны. Например, в состоянии всестороннего сжатия находятся тела, погруженные в жидкость. В случае погружения тел на большую глубину в море деформация всестороннего сжатия велика, и это имеет значение для живущих там животных. Реже встречается всестороннее растяжение. В состоянии всестороннего растяжения находится, например, внутренняя часть холодного железного шара, опущенного в горячую воду. Большое значение имеют деформации всестороннего сжатия и растяжения при распространении звуковых колебаний (о которых будет идти речь в разделе «Колебания и волны» тома III).
280.1.
Как изменится удлинение, если, не меняя нагрузки, проволоку заменить другой из такого же материала, имеющей вдвое большие длину и диаметр?
280.2.
Опыт показывает, что стальная проволока площади сечения
и длины 1 м при растяжении силой 200 Н удлиняется на 1 мм. Какое удлинение получится, если стальную проволоку площади сечения
и длины 3 м растягивать силой 300Н?
Источник
Частицы, из которых состоят твердые тела (как аморфные, так и кристаллические) постоянно совершают тепловые колебания около положений равновесия. В таких положениях энергия их взаимодействия минимальная. Если расстояние между частицами уменьшается, начинают действовать силы отталкивания, а если увеличиваться – то силы притяжения. Именно этими двумя силами обусловлены все механические свойства, которыми обладают твердые тела.
Определение 1
Если твердое тело изменяется под воздействием внешних сил, то частицы, из которых оно состоит, меняют свое внутреннее положение. Такое изменение называется деформацией.
Виды деформации
Различают деформации нескольких видов. На изображении показаны некоторые из них.
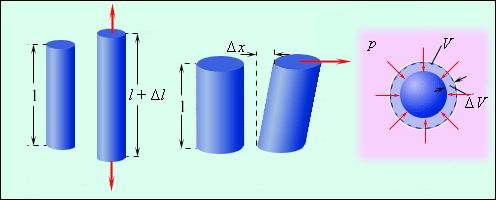
Рисунок 3.7.1. Некоторые виды деформаций твердых тел: 1 – деформация растяжения; 2 – деформация сдвига; 3 – деформация всестороннего сжатия.
Первый вид – растяжение или сжатие – является наиболее простым видом деформации. В таком случае изменения, происходящие с телом, можно описать при помощи абсолютного удлинения Δl, которое происходит под действием сил, обозначаемых F→. Взаимосвязь, существующая между силами и удлинением, обусловлена геометрическими размерами тела (в первую очередь толщиной и длиной), а также механическими свойствами вещества.
Определение 2
Если мы разделим величину абсолютного удлинения на первоначальную длину твердого тела, мы получим величину его относительного удлинения (относительной деформации).
Обозначим этот показатель ε и запишем следующую формулу:
ε=∆ll.
Определение 3
Относительная деформация тела растет при его растяжении и соответственно уменьшается при сжатии.
Если учесть, в каком именно направлении внешняя сила действует на тело, то мы можем записать, что F будет больше нуля при растяжении и меньше нуля при сжатии.
Механическое напряжение
Определение 4
Механическое напряжение твердого тела σ – это показатель, равный отношению модуля внешней силы к площади сечения твердого тела.
σ=FS.
Величину механического напряжения принято выражать в паскалях (Па) и измерять в единицах давления.
Важно понимать, как именно механическое напряжение и относительная деформация связаны между собой. Если отобразить их взаимоотношения графически, мы получим так называемую диаграмму растяжения. При этом нам нужно отмерить величину относительной деформации по оси x, а механическое напряжение – по оси y. На рисунке ниже представлена диаграмма растяжения, типичная для меди, мягкого железа и некоторых других металлов.

Рисунок 3.7.2. Типичная диаграмма растяжения для пластичного материала. Голубая полоса – область упругих деформаций.
В тех случаях, когда деформация твердого тела меньше 1% (малая деформация), то связь между относительным удлинением и механическим напряжением приобретает линейный характер. На графике это показано на участке Oa. Если напряжение снять, то деформация исчезнет.
Определение 5
Деформация, исчезающая при снятии напряжения, называется упругой.
Линейный характер связи сохраняется до определенного предела. На графике он обозначен точкой a.
Определение 6
Предел пропорциональности – это наибольшее значение σ=σпр, при котором сохраняется линейная связь между показателями σ и ε.
На данном участке будет выполняться закон Гука:
ε=1Eσ.
В формуле содержится так называемый модуль Юнга, обозначенный буквой E.
Если мы продолжим увеличивать напряжение на твердое тело, то линейный характер связи нарушится. Это видно на участке ab. Сняв напряжение, мы также увидим практически полное исчезновение деформации, то есть восстановление формы и размеров тела.
Предел упругости
Определение 7
Предел упругости – максимальное напряжение, после снятия которого тело восстановит свою форму и размер.
После перехода этого предела восстановления первоначальных параметров тела уже не происходит. Когда мы снимаем напряжение, у тела остается так называемая остаточная (пластическая) деформация.
Определение 8
Обратите внимание на участок диаграммы bc, где напряжение практически не увеличивается, но деформация при этом продолжается. Это свойство называется текучестью материала.
Предел прочности
Определение 9
Предел прочности – максимальное напряжение, которое способно выдержать твердое тело, не разрушаясь.
В точке e материал разрушается.
Определение 10
Если диаграмма напряжения материала имеет вид, соответствующий тому, что показан на графике, то такой материал называется пластичным. У них обычно деформация, при которой происходит разрушение, заметно больше области упругих деформаций. К пластичным материалам относится большинство металлов.
Определение 11
Если материал разрушается при деформации, которая превосходит область упругих деформаций незначительно, то он называется хрупким. Такими материалами считаются чугун, фарфор, стекло и др.
Деформация сдвига имеет аналогичные закономерности и свойства. Ее отличительная особенность состоит в направлении вектора силы: он направлен по касательной относительно поверхности тела. Для поиска величины относительной деформации нам нужно найти значение Δxl, а напряжения – FS (здесь буквой S обозначена та сила, которая действует на единицу площади тела). Для малых деформаций действует следующая формула:
∆xl=1GFS
Буквой G в формуле обозначен коэффициент пропорциональности, также называемый модулем сдвига. Обычно для твердого материала он примерно в 2-3 раза меньше, чем модуль Юнга. Так, для меди E=1,1·1011 Н/м2, G=0,42·1011 Н/м2.
Когда мы имеем дело с жидкими и газообразными веществами, то важно помнить, что у них модуль сдвига равен 0.
При деформации всестороннего сжатия твердого тела, погруженного в жидкость, механическое напряжение будет совпадать с давлением жидкости (p). Чтобы вычислить относительную деформацию, нам нужно найти отношение изменения объема ΔV к первоначальному объему V тела. При малых деформациях
∆VV=1Bp
Буквой B обозначен коэффициент пропорциональности, называемый модулем всестороннего сжатия. Такому сжатию можно подвергнуть не только твердое тело, но и жидкость и газ. Так, у воды B=2,2·109 Н/м2, у стали B=1,6·1011Н/м2. В Тихом океане на глубине 4 км давление составляет 4·107 Н/м2, а относительно изменения объема воды 1,8 %. Для твердого тела, изготовленного из стали, значение этого параметра равно 0,025 %, то есть оно меньше в 70 раз. Это подтверждает, что твердые тела благодаря жесткой кристаллической решетке обладают гораздо меньшей сжимаемостью по сравнению с жидкостью, в которой атомы и молекулы связаны между собой не так плотно. Газы могут сжиматься еще лучше, чем тела и жидкости.
От значения модуля всестороннего сжатия зависит скорость, с которой звук распространяется в данном веществе.
Источник
