При растяжении стержня длиной 70 см среднее расстояние между атомами

- Главная
- Вопросы & Ответы
- Вопрос 6485842
Главный Попко
более месяца назад
Просмотров : 42
Ответов : 1
Лучший ответ:
Таня Масян
comment
более месяца назад
Ваш ответ:
Комментарий должен быть минимум 20 символов
Чтобы получить баллы за ответ войди на сайт

Лучшее из галереи за : неделю месяц все время































Другие вопросы:
Зачетный Опарыш
Снежная королева посетила 36 деревень, городов в 4 раза меньше, чем деревень, сёл на 7 больше, чем городов, а посёлков столько, сколько городов, деревень Снежная королева посетила 36 деревень, городов в 4 раза меньше, чем деревень, сёл на 7 больше, чем городов, а посёлков столько, сколько городов, д…
более месяца назад
Смотреть ответ
Просмотров : 16
Ответов : 1
Суррикат Мими
У Кая было 54 осколка льда, из которых он хотел собрать слово «вечность»: 18 треугольных осколков, столько же четырёхугольных, а остальные осколки У Кая было 54 осколка льда, из которых он хотел собрать слово «вечность»: 18 треугольных осколков, столько же четырёхугольных, а остальные осколки — пяти…
более месяца назад
Смотреть ответ
Просмотров : 34
Ответов : 1
Васян Коваль
На службе у Снежной королевы было 18 вьюг, 14 метелей, а буранов в 4 раза меньше, чем вьюг и метелей вместе. Сколько буранов было на службе у Снежной королевы? На службе у Снежной королевы было 18 вьюг, 14 метелей, а буранов в 4 раза меньше, чем вьюг и метелей вместе. Сколько буранов было на службе…
более месяца назад
Смотреть ответ
Просмотров : 18
Ответов : 1
Онтонио Веселко
Начерти прямоугольник, длина которого 6 см, а ширина в 3 раза меньше. Найди его периметр. Начерти прямоугольник, длина которого 6 см, а ширина в 3 раза меньше. Найди его периметр.
более месяца назад
Смотреть ответ
Просмотров : 14
Ответов : 2
Мари Умняшка
Начерти 2 отрезка: длина одного 3 см, а длина второго отрезка в 4 раза больше. Найди длину второго отрезка. Начерти 2 отрезка: длина одного 3 см, а длина второго отрезка в 4 раза больше. Найди длину второго отрезка.
более месяца назад
Смотреть ответ
Просмотров : 12
Ответов : 1
Источник
Опубликовано пт, 07/19/2019 — 07:55 пользователем fizportal.ru
СВОЙСТВА ТЕЛ. Деформации твердых тел. Тема 15-3
15.35. Каким должен быть диаметр d стержня крюка подъемного крана, чтобы при подъеме с постоянной скоростью груза весом P = 25 кН возникающее напряжение не превышало σ = 6,0 × 107 Па?
15.36. Каково напряжение σ, возникающее у основания кирпичной стены высотой h = 20 м? Плотность кирпича ρ = 1,8 × 103 кг/м3.
15.37. Два стержня одинакового материала и сечения имеют различную длину (L2 < L1). Определите, одинаково ли их относительное удлинение ε под действием одинаковых сил. К какому из стержней нужно приложить большую силу для получения одинакового абсолютного удлинения ΔL? Массой стержней пренебречь.
Ответ
Одинаково. Ко второму стержню нужно приложить большую силу
15.38. Как отличаются относительные удлинения двух проволок из одного и того же материала при одинаковых нагрузках, если длина и диаметр первой из них в два раза больше, чем у второй? Как отличаются их абсолютные удлинения? Массой проволок пренебречь.
Ответ
У первой проволоки относительное удлинение в 4 раза, а абсолютное в 2 раза меньше, чем у второй
15.39. Какой запас прочности n = σ пр/σ имеет стальной стержень сечением S = 3,0 см2, к которому подвешен груз массы m = 7,5 т, если разрушающая нагрузка для данной марки стали при растяжении равна σпр = 6,0 × 108 Па? Массу стержня не учитывать.
15.40. Какая пружина стальная или медная при упругой деформации под действием одинаковой деформирующей силы приобретает большую потенциальную энергию? Внешне пружины абсолютно одинаковы. Массой пружин пренебречь. Модуль упругости меди меньше, чем у стали: Eм < Eм.
Ответ
Потенциальная энергия медной пружины больше Uм/ Uc = Eс/ Eм > 1
15.41. Медный цилиндрический стержень длины Lo подвешен за один конец к потолку. Определите удлинение ΔL стержня под действием его собственного веса, если плотность ρ и модуль Юнга E для меди считать известными.
15.42. Медный брусок длины Lo и площади поперечного сечения S лежит на гладком столе. Если брусок тянуть за один из концов с силой F, равномерно распределенной по сечению торца, то его длина увеличится на ΔL. Определите из этих условий модуль Юнга E для меди.
15.43. Между двумя столбами натянута с небольшим усилием легкая проволока. К проволоке посередине подвешивают фонарь массой m. Площадь поперечного сечения проволоки равна S, модуль упругости материала E. Найдите угол провисания проволоки, считая его малым.
15.44. Железобетонная колона сжата силой F. Какая часть нагрузки приходится на железо, если площадь поперечного сечения железа в 20 раз меньше площади поперечного сечения бетона, а модуль упругости железа в 10 раз больше модуля упругости бетона?
15.45. Из скольких стальных проволок диаметром 2 мм должен состоять трос, рассчитанный на подъем груза массой 16 т?
15.46. Какую силу надо приложить к концам стального стержня площадью поперечного сечения 10 см2, чтобы не дать ему расширится при нагревании от 0 °С до 30 °С?
15.47. К стальной проволоке радиусом 1 мм подвешен груз. Под действием этого груза проволока получила такое же удлинение, как при нагревании на 20 °С. Найти массу груза.
15.48. Медная проволока натянута горячей при температуре 150 °С между двумя прочными неподвижными стенками. При какой температуре, остывая, разорвется проволока? Считать, что закон Гука справедливым вплоть до разрыва стержня.
15.49. При нагревании некоторого металла от 0 °С до 500 °С его плотность уменьшается в 1,027 раза. Найти для этого металла коэффициент линейного расширения, считая его постоянным в данном интервале температур.
15.50. На нагревание медной болванки массой 1 кг, находящейся при температуре 0 °С, затрачено количество теплоты 138,2 кДж. Во сколько раз при этом увеличится ее объем?
5.51. Каким должен быть предельный диаметр стального троса, чтобы он выдержал нагрузку 9,8 кН?
15.52. Найти длину медной проволоки, которая, будучи подвешенной вертикально, начинает рваться под действием собственной силы тяжести.
15.53. Для измерения глубины моря с парохода спустили гирю на стальном тросе. Какую наибольшую глубину можно измерить таким способом?
15.54. С крыши дома свешивается стальная проволока длиной 40 м и диаметром 2 мм. Какую нагрузку может выдержать эта проволока? На сколько удлинится эта проволока, если на ней повиснет человек массой 70 кг? Будет ли наблюдаться остаточная деформация, когда человек отпустит проволоку? Предел упругости стали 294 МПа.
15.55. К стальной проволоке радиусом 1 мм подвешен груз массой 100 кг. На какой наибольший угол можно отклонить проволоку с грузом, чтобы она не разорвалась при прохождении положения равновесия?
15.56. К железной проволоке длиной 50 см и диаметром 1 мм привязана гиря массой 1 кг. С какой частотой можно равномерно вращать в вертикальной плоскости такую проволоку с грузом, чтобы она не разорвалась?
15.57. К стальной проволоке длиной 1 м и радиусом 1 мм подвесили груз массой 100 кг. Найти работу растяжения проволоки.
15.58. Из резинового шнура длиной 42 см и радиусом 3 мм сделана рогатка. Мальчик, стреляя из рогатки, растянул резиновый шнур на 20 см. Найти модуль Юнга для этой резины, если известно, что камень массой 0,02 кг, пущенный из рогатки полетел со скоростью 20 м/с. Изменением сечения шнура при растяжении пренебречь.
Источник
1.1 (Вариант 4) Конструкция состоит из двух стержней, соединенных между собой и с основанием шарнирами (рис.1). К шарнирному болту С привязан груз Р. Требуется определить внутренние усилия в стержнях и подобрать их сечение по допускаемым напряжениям на сжатие и растяжение. Величина силы Р, форма сечения и допускаемые напряжения приведены в табл.1. 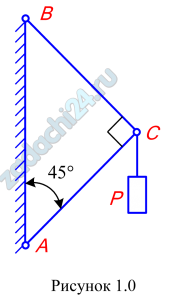
Таблица 1
| Сечение стержней | Величина Р, кН | [σ]С, МПа | [σ]Р, МПа |
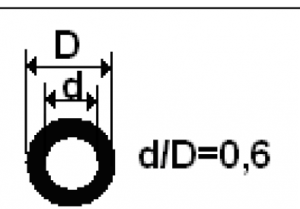 | 10 | 160 | 100 |
Ответ: NBC=7,1 кН, NAC=-7,1 кН, D=15,0 мм, d=9,0 мм.
1.2 (Вариант 29) Двухступенчатый стальной брус, длины ступеней которого указаны на рис.23 (схемы I-X) нагружены силами F1 и F2. Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить удлинение (укорочение) бруса, приняв Е=2·105 МПа. Числовые значения сил F1 и F2, а также площадей поперечных сечений ступеней A1 и A2 для своего варианта взять из табл.8.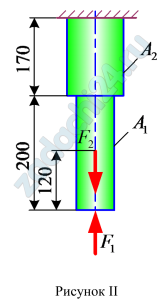
Таблица 8 — Исходные данные
| № задачи и схемы на рис.23 | F1, кН | F2, кН | А1, см2 | А2, см2 |
| 62,II | 4,8 | 10,0 | 0,4 | 0,8 |
Ответ: Δl=0,113·10-3 м.
1.3 (Вариант 2396) Для консольного бруса переменного сечения (рис.3.1) построить эпюры нормальной силы, нормальных напряжений и продольных перемещений. Определить из условия прочности допустимое значение нагрузки F и при найденном значении нагрузки вычислить наибольшее перемещение бруса, а также максимальное удлинение участка a.
Принять А=200 мм², l=200 мм, s=2, остальные данные взять из табл.3.1 и табл.3.2.
Источник
