При растяжении пружины потенциальная энергия уменьшается
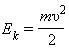
Встречается довольно большое количество различных механизмов, частью которых является пружина. Этот конструктивный элемент характеризуется довольно большим количество различных особенностей, которые должны учитываться. Примером можно назвать понятие потенциальной энергии пружины. Рассмотрим все особенности данного вопроса подробнее.
Понятие потенциальной энергии пружины
При рассмотрении того, что такое потенциальная энергия пружины следует уделить внимание самому понятию – свойство, которым могут обладать тела при нахождении на земле. Этот момент определяет то, что ей могут обладать самые разнообразные изделия, в том числе рассматриваемое. К особенностям рассматриваемого понятия можно отнести следующее:
- Потенциальная энергия в рассматриваемом случае формируется по причине изменения состояния. Даже при несущественном смещении витков относительно друг друга считается изменением состояния подобного изделия.
- Для того чтобы изменить состояние изделия совершается определенное действие. Зачастую для этого проводится прикладывание усилия. При этом важно провести расчет требуемого усилия для сжатия витков.
- После выполнения определенной работы большая часть усилия, которое было потрачено на выполнение действия высвобождается при определенных обстоятельствах. Как правило, этот процесс предусматривает возврат витков в свое первоначальное положение. Это достигается за счет особой формы изделия, а также применения соответствующего материала, который обладает повышенной упругостью. Именно за счет этого свойства зачастую проводится установка рассматриваемого изделия. Показатель может достигать весьма высоких показателей, которой достаточно для реализации различных задач. Распространенным примером можно назвать установку пружины в запорных и предохранительных элементах, которые отвечают за непосредственное возращение запорного элемента в требуемое положение.
Она также широко применяется при создании самых различных механизмов, к примеру, заводных часов. При проектировании различных механизмов учитывается закон сохранения механической силы, которая характеризуется довольно большим количеством особенностей.
Закон сохранения механической энергии
Согласно установленным законам механическое воздействие консервативной механической системы сохраняется во времени. Этот момент определяет то, что потенциальная энергия деформированной пружины не может возникнуть сама или исчезнуть куда-нибудь. Именно поэтому для ее создания нужно приложить соответствующее усилие.
Рассматриваемый закон относится к категории интегральных равенств. Эта закономерность определяет то, что он складывается их действия дифференциальных законов, является свойством или признаком совокупного воздействия.
Для проведения соответствующих расчетов должна применяться определенная формула. Сила, с которой оказывается воздействие, не является постоянной. Именно поэтому для ее вычисления применяется графический метод. Самая простая зависимость может быть описана следующим образом: F=kx. При применении подобной зависимости построенная координатная линия будет представлена прямой линией, которая расположена под углом относительно системы координат.
Приписать подобному устройству потенциальную энергию можно только в том случае, если она равна максимальной работе и не зависит от условной траектории движения. Проведенные исследования указывают на то, что подобная работа подчиняется закону Гука. Для определения основного показателя применяется следующая формула: U=kk2/2.
Для деформирования витков к ним должно быть приложено определенное усилие, так как в противном случае кинетическая сила не возникнет.
Динамика твердого тела
Некоторые определить выражения (определяется при применении наиболее подходящих формул) можно только с учетом правил, касающихся динамики твердых объектов. Этому вопросу посвящен целый раздел. При расчете потенциальной энергии сжатой пружины также применяются некоторые законы этого раздела
Динамика твердого тела рассматривается по причине того, что в большинстве случаев механизм совершает действие, связанное с непосредственным перемещением какого-либо объекта.
Рассматриваемое свойство изделия может изменяться в зависимости от динамики твердого тела. Это связано с тем, что на изделие оказывается и воздействие со стороны окружающей среды. Примером можно назвать трение или нагрев.
Момент силы и момент импульса относительно оси
Рассмотрение деформации пружины проводится также с учетом момента силы и импульса относительно оси. Эти два параметра позволяют рассчитать все требуемые показатели с более высокой точностью. Довольно распространенным вопросом можно назвать чему равен момент силы – векторная величина, которая определяется векторному произведению радиуса на вектор приложенной силы.
Момент импульса – величина, которая применяется для определения количества вращательного движения.
Среди особенностей подобного показателя можно отметить следующее:
- Масса вращения. Объект может характеризоваться различной массой.
- Распределение относительно оси. Ось может быть расположена на различном расстоянии от самого объекта.
- Скорость вращения. Это свойство считается наиболее важным, в зависимости от конструкции он может быть постоянным или изменяться.
Расчет каждого показателя проводится при применении соответствующей формулы. В некоторых случаях проводится измерение требуемых вводных данных, без которых провести вычисления не получится.
Уравнение движения вращающегося тела
Рассматривая подобное свойство также следует уделить внимание уравнению движения вращающегося тела. Не стоит забывать о том, что вращательное движение твердого тела характеризуется наличием как минимум двух точек. При этом отметим нижеприведенные особенности:
- Прямая, которая соединяет две точки, выступает в качестве оси вращения.
- Есть возможность провести определение места положения объекта в случае вычисления заднего угла между двумя плоскостями.
- Наиболее важным показателем можно назвать угловую скорость. Она связана с инерцией, которая возникает при вращении объекта.
Для вычисления угловой скорости применяется специальная формула, которая выглядит следующим образом: w=df/dt. В некоторых случаях проводится вычисление углового ускорения, которое также является важной величиной.
Источник
Все формулы по физике и математике
Темы по физике
- Механика (56)
- Кинематика (19)
- Динамика и статика (32)
- Гидростатика (5)
Темы по математике
- Квадратный корень, рациональные переходы (1)
- Квадратный трехчлен (1)
- Координатный метод в стереометрии (1)
- Логарифмы (1)
- Логарифмы, рациональные переходы (1)
- Модуль (1)
- Модуль, рациональные переходы (1)
- Планиметрия (1)
- Прогрессии (1)
- Производная функции (1)
- Степени и корни (1)
- Стереометрия (1)
- Тригонометрия (1)
- Формулы сокращенного умножения (1)
Потенциальная энергия упруго деформированного тела — физическая величина, равная половине произведения жесткости тела на квадрат его деформации.
Энергию деформированного упругого тела также называют энергией положения или потенциальной энергией (ее называют чаще упругой энергией), так как она зависит от взаимного положения частей тела, например витков пружины. Работа, которую может совершить растянутая пружина при перемещении ее конца, зависит только от начального и конечного растяжений пружины. Найдем работу, которую может совершить растянутая пружина, возвращаясь к не растянутому состоянию, то есть найдем упругую энергию растянутой пружины.
Потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.
Из этой формулы видно, что, растягивая с одной и той же силой разные пружины, мы сообщим им различный запас потенциальной энергии: чем жестче пружина, то есть чем больше коэффициент упругости, тем меньше потенциальная энергия; и наоборот: чем мягче пружина, тем больше энергия, которую она запасет при данной силе, растянувшей ее. Это можно уяснить себе наглядно, если учесть, что при одинаковых действующих силах растяжение мягкой пружины больше, чем жесткой, а потому больше и произведение силы на путь точки приложения силы.
Потенциальная энергия :
Кинетическая энергия
Тут мы использовали :
— Потенциальная энергия упруго деформированного тела
— Коэффициент упругости пружины
— Деформация пружины
Груз массой m, подвешенный к пружине, совершает колебания с периодом T и амплитудой Что произойдет с периодом колебаний, максимальной потенциальной энергией пружины и частотой колебаний, если при неизменной амплитуде уменьшить массу груза?
Для каждой величины определите соответствующий характер изменения:
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Период колебаний | Максимальная потенциальная |
энергия пружины
Период колебаний связан с массой груза и жесткостью пружины k соотношением При уменьшении массы период колебаний уменьшится. Частота обратно пропорциональна периоду, значит, частота увеличится.
С максимальной потенциальной энергией пружины все немного сложнее. Для ответа на вопрос, что с ней произойдет существенно, что пружина ориентирована вертикально (для горизонтального пружинного маятника при неизменной амплитуде данная величина, естественно, останется неизменной). Действительно, когда к вертикальной пружине подвешивают груз, она сразу немного растягивается, чтобы уравновесить силу тяжести, действующую на груз. Определим это начальное растяжение: Именно это состояние является положением равновесия для вертикального пружинного маятника, колебания происходят вокруг него, груз поднимается и опускается из этого положения на величину амплитуды. При движении вниз из положения равновесия пружина продолжает растягиваться, а значит, потенциальная энергия пружины продолжает увеличиваться. При движении вверх из положения равновесия, сперва деформация пружины уменьшается, а если то пружины начнет сжиматься. Максимальной потенциальной энергии пружины соответствует состояние, когда она максимально растянута, а значит, в нашем случае, это положение, когда груз опустился максимально вниз. Таким образом, максимальная потенциальная энергия пружины равна
Из этой формулы видно, что для вертикального пружинного маятника при неизменной амплитуде и уменьшении массы груза максимальная потенциальная энергия пружины уменьшится.
Встречается довольно большое количество различных механизмов, частью которых является пружина. Этот конструктивный элемент характеризуется довольно большим количество различных особенностей, которые должны учитываться. Примером можно назвать понятие потенциальной энергии пружины. Рассмотрим все особенности данного вопроса подробнее.
Понятие потенциальной энергии пружины
При рассмотрении того, что такое потенциальная энергия пружины следует уделить внимание самому понятию – свойство, которым могут обладать тела при нахождении на земле. Этот момент определяет то, что ей могут обладать самые разнообразные изделия, в том числе рассматриваемое. К особенностям рассматриваемого понятия можно отнести следующее:
- Потенциальная энергия в рассматриваемом случае формируется по причине изменения состояния. Даже при несущественном смещении витков относительно друг друга считается изменением состояния подобного изделия.
- Для того чтобы изменить состояние изделия совершается определенное действие. Зачастую для этого проводится прикладывание усилия. При этом важно провести расчет требуемого усилия для сжатия витков.
- После выполнения определенной работы большая часть усилия, которое было потрачено на выполнение действия высвобождается при определенных обстоятельствах. Как правило, этот процесс предусматривает возврат витков в свое первоначальное положение. Это достигается за счет особой формы изделия, а также применения соответствующего материала, который обладает повышенной упругостью. Именно за счет этого свойства зачастую проводится установка рассматриваемого изделия. Показатель может достигать весьма высоких показателей, которой достаточно для реализации различных задач. Распространенным примером можно назвать установку пружины в запорных и предохранительных элементах, которые отвечают за непосредственное возращение запорного элемента в требуемое положение.
Она также широко применяется при создании самых различных механизмов, к примеру, заводных часов. При проектировании различных механизмов учитывается закон сохранения механической силы, которая характеризуется довольно большим количеством особенностей.
Закон сохранения механической энергии
Согласно установленным законам механическое воздействие консервативной механической системы сохраняется во времени. Этот момент определяет то, что потенциальная энергия деформированной пружины не может возникнуть сама или исчезнуть куда-нибудь. Именно поэтому для ее создания нужно приложить соответствующее усилие.
Рассматриваемый закон относится к категории интегральных равенств. Эта закономерность определяет то, что он складывается их действия дифференциальных законов, является свойством или признаком совокупного воздействия.
Для проведения соответствующих расчетов должна применяться определенная формула. Сила, с которой оказывается воздействие, не является постоянной. Именно поэтому для ее вычисления применяется графический метод. Самая простая зависимость может быть описана следующим образом: F=kx. При применении подобной зависимости построенная координатная линия будет представлена прямой линией, которая расположена под углом относительно системы координат.
Приписать подобному устройству потенциальную энергию можно только в том случае, если она равна максимальной работе и не зависит от условной траектории движения. Проведенные исследования указывают на то, что подобная работа подчиняется закону Гука. Для определения основного показателя применяется следующая формула: U=kk2/2.
Для деформирования витков к ним должно быть приложено определенное усилие, так как в противном случае кинетическая сила не возникнет.
Динамика твердого тела
Некоторые определить выражения (определяется при применении наиболее подходящих формул) можно только с учетом правил, касающихся динамики твердых объектов. Этому вопросу посвящен целый раздел. При расчете потенциальной энергии сжатой пружины также применяются некоторые законы этого раздела
Динамика твердого тела рассматривается по причине того, что в большинстве случаев механизм совершает действие, связанное с непосредственным перемещением какого-либо объекта.
Рассматриваемое свойство изделия может изменяться в зависимости от динамики твердого тела. Это связано с тем, что на изделие оказывается и воздействие со стороны окружающей среды. Примером можно назвать трение или нагрев.
Момент силы и момент импульса относительно оси
Рассмотрение деформации пружины проводится также с учетом момента силы и импульса относительно оси. Эти два параметра позволяют рассчитать все требуемые показатели с более высокой точностью. Довольно распространенным вопросом можно назвать чему равен момент силы – векторная величина, которая определяется векторному произведению радиуса на вектор приложенной силы.
Момент импульса – величина, которая применяется для определения количества вращательного движения.
Среди особенностей подобного показателя можно отметить следующее:
- Масса вращения. Объект может характеризоваться различной массой.
- Распределение относительно оси. Ось может быть расположена на различном расстоянии от самого объекта.
- Скорость вращения. Это свойство считается наиболее важным, в зависимости от конструкции он может быть постоянным или изменяться.
Расчет каждого показателя проводится при применении соответствующей формулы. В некоторых случаях проводится измерение требуемых вводных данных, без которых провести вычисления не получится.
Уравнение движения вращающегося тела
Рассматривая подобное свойство также следует уделить внимание уравнению движения вращающегося тела. Не стоит забывать о том, что вращательное движение твердого тела характеризуется наличием как минимум двух точек. При этом отметим нижеприведенные особенности:
- Прямая, которая соединяет две точки, выступает в качестве оси вращения.
- Есть возможность провести определение места положения объекта в случае вычисления заднего угла между двумя плоскостями.
- Наиболее важным показателем можно назвать угловую скорость. Она связана с инерцией, которая возникает при вращении объекта.
Для вычисления угловой скорости применяется специальная формула, которая выглядит следующим образом: w=df/dt. В некоторых случаях проводится вычисление углового ускорения, которое также является важной величиной.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Источник
Лабораторная работа № 3
Тема: «Сохранение механической энергии при движении тела под действием сил тяжести и упругости»
Цель: 1) научиться измерять потенциальную энергию поднятого над землей тела и упруго деформированной пружины;
2) сравнить две величины—уменьшение потенциальной энергии прикрепленного к пружине тела при его падении и увеличение потенциальной энергии растянутой пружины.
Приборы и материалы: 1) динамометр, жесткость пружины которого равна 40 Н/м; 2) линейка измерительная; 3) груз из набора по механике; масса груза равна (0,100 ±0,002) кг; 4) фиксатор; 5) штатив с муфтой и лапкой.
Основные сведения.
Если тело способно совершить работу, то говорят, что оно обладает энергией.
Механическая энергия тела – это скалярная величина, равная максимальной работе, которая может быть совершена в данных условиях.
Обозначается Е Единица энергии в СИ [1Дж = 1Н*м]
Кинетическая энергия – это энергия тела, обусловленная его движением.
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:
![]()
Кинетическая энергия – это энергия движения. Кинетическая энергия тела массой m, движущегося со скоростью ![]() равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:
равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:
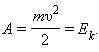
Наряду с кинетической энергией или энергией движения в физике важную роль играет понятие потенциальной энергии или энергии взаимодействия тел.
Потенциальная энергия – энергия тела, обусловленная взаимным расположением взаимодействующих между собой тел или частей одного тела.
Потенциальная энергия тела в поле силы тяжести (потенциальная энергия тела, поднятого над землёй).
Ep = mgh
Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень.
Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, то есть сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Потенциальной энергией пружины (или любого упруго деформированного тела) называют величину
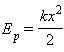 , где k – жесткость пружины, х — абсолютное удлинение тела.
, где k – жесткость пружины, х — абсолютное удлинение тела.
Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией.
Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой силами упругости.
Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только силами тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:
A = –(Ep2 – Ep1).
По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел:
A = Ek2 – Ek1
Следовательно Ek2 – Ek1 = –(Ep2 – Ep1) или Ek1 + Ep1 = Ek2 + Ep2.
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной.
Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона.
Сумму E = Ek + Ep называют полной механической энергией.
Полная механическая энергия замкнутой системы тел, взаимодействующих между собой только консервативными силами, при любых движениях этих тел не изменяется. Происходят лишь взаимные превращения потенциальной энергии тел в их кинетическую энергию, и наоборот, или переход энергии от одного тела к другому.
Е = Ек + Еp = const
Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.
В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими консервативными силами действуют силы трения или силы сопротивления среды.
Сила трения не является консервативной. Работа силы трения зависит от длины пути.
Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).
Описание установки.
Для работы используется установка, показанная на рисунке. Она представляет собой укрепленный на штативе динамометр с фиксатором 1.
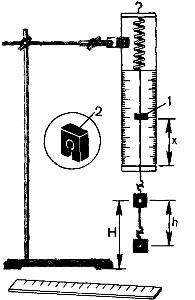
Пружина динамометра заканчивается проволочным стержнем с крючком. Фиксатор (в увеличенном масштабе он показан отдельно — помечен цифрой 2) — это легкая пластинка из пробки (размерами 5 Х 7 X 1,5 мм), прорезанная ножом до ее центра. Ее насаживают на проволочный стержень динамометра. Фиксатор должен перемещаться вдоль стержня с небольшим трением, но трение все же должно быть достаточным, чтобы фиксатор сам по себе не падал вниз. В этом нужно убедиться перед началом работы. Для этого фиксатор устанавливают у нижнего края шкалы на ограничительной скобе. Затем растягивают и отпускают.
Фиксатор вместе с проволочным стержнем должен подняться вверх, отмечая этим максимальное удлинение пружины, равное расстоянию от упора до фиксатора.
Если поднять груз, висящий на крючке динамометра, так, чтобы пружина не была растянута, то потенциальная энергия груза по отношению, например, к поверхности стола равна mgh. При падении груза (опускание на расстояние x = h) потенциальная энергия груза уменьшится на
Е1=mgh
а энергия пружины при ее деформации увеличивается на
Е2=kx2/2
Порядок выполнения работы
1. Груз из набора по механике прочно укрепите на крючке динамометра.
2. Поднимите рукой груз, разгружая пружину, и установите фиксатор внизу у скобы.
3. Отпустите груз. Падая, груз растянет пружину. Снимите груз и по положению фиксатора измерьте линейкой максимальное удлинение х пружины.
4. Повторите опыт пять раз. Найдите среднее значение h и х
5. Подсчитайте Е1ср=mgh и Е2ср=kx2/2
6. Результаты занесите в таблицу:
№ опыта | h=хmax, | hср=хср, | Е1ср, | Е2ср, | Е1ср/ Е2ср |
1 | |||||
2 | |||||
3 | |||||
4 | |||||
5 |
7. Сравните отношение Е1ср/ Е2ср с единицей и сделайте вывод о погрешности, с которой был проверен закон сохранения энергии.
8. Ответьте на контрольные вопросы.
Контрольные вопросы.
1.Раскройте понятие механической энергии?
2.Какая энергия называется кинетической? По какой формуле она находится?
3.Какая энергия называется потенциальной? По какой формуле она находится?
4. Что называется полной механической энергией?
5.Сформулируйте закон сохранения механической энергии.
6. Как связано изменение потенциальной энергии падающего груза с изменением энергии
пружины, растянутой при его падении?
Вариант выполнения измерений.
1. Определяем максимальное удлинение х пружины и заносим в таблицу:
№ опыта | h=хmax, | hср=хср, | Е1ср, | Е2ср, | Е1ср/ Е2ср |
1 | 0,048 | ||||
2 | 0,054 | ||||
3 | 0,052 | ||||
4 | 0,050 | ||||
5 | 0,052 |
2. Выполняем расчеты по методичке.
Источник
