Правило знаков при растяжении
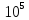
Внутренние усилия при растяжении-сжатии.
Осевое (центральное) растяжение или сжатие прямого бруса вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса. При растяжении или сжатии в поперечных сечениях бруса возникают только продольные силы N. Продольная сила N в некотором сечении равна алгебраической сумме проекции на ось стержня всех внешних сил, действующих по одну сторону от рассматриваемого сечения. По правилу знаков продольной силы N принято считать, что от растягивающих внешних нагрузок возникают положительные продольные силы N, а от сжимающих — продольные силы N отрицательны (рис. 5).

Чтобы выявить участки стержня или его сечения, где продольная сила имеет наибольшее значение, строят эпюру продольных сил, применяя метод сечений, подробно рассмотренный в статье:
Анализ внутренних силовых факторов в статистически определимых системах
Ещё настоятельно рекомендую взглянуть на статью:
Расчёт статистически определимого бруса
Если разберёте теорию в данной статье и задачи по ссылкам, то станете гуру в теме «Растяжение-сжатие» =)
Напряжения при растяжении-сжатии.
Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:

где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.
Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:

Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.
Деформации при растяжении-сжатии.
Рассмотрим деформации, возникающие при растяжении (сжатии) стержня (рис.6, а). Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l1 и его длины до деформации l

Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением, или относительной продольной деформацией:

При растяжении продольная деформация положительна, а при сжатии – отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:

где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).
Таблица 1
Модуль продольной упругости для различных материалов

Абсолютная поперечная деформация бруса равна разности размеров поперечного сечения после и до деформации:

Соответственно, относительную поперечную деформацию определяют по формуле:

При растяжении размеры поперечного сечения бруса уменьшаются, и ε’ имеет отрицательное значение. Опытом установлено, что в пределах действия закона Гука при растяжении бруса поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε’ к продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона μ:

Экспериментально установлено, что на упругой стадии нагружения любого материала значение μ = const и для различных материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5 (табл. 2).
Таблица 2
Коэффициент Пуассона.

Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N:

Данной формулой можно пользоваться для вычисления абсолютного удлинения участка стержня длиной l при условии, что в пределах этого участка значение продольной силы постоянно. В случае, когда продольная сила N изменяется в пределах участка стержня, Δl определяют интегрированием в пределах этого участка:

Произведение (Е·А) называют жесткостью сечения стержня при растяжении (сжатии).
Механические свойства материалов.
Основными механическими свойствами материалов при их деформации являются прочность, пластичность, хрупкость, упругость и твердость.
Прочность — способность материала сопротивляться воздействию внешних сил, не разрушаясь и без появления остаточных деформаций.
Пластичность – свойство материала выдерживать без разрушения большие остаточные деформации. Неисчезающие после снятия внешних нагрузок деформации называются пластическими.
Хрупкость – свойство материала разрушаться при очень малых остаточных деформациях (например, чугун, бетон, стекло).
Идеальная упругость – свойство материала (тела) полностью восстанавливать свою форму и размеры после устранения причин, вызвавших деформацию.
Твердость – свойство материала сопротивляться проникновению в него других тел.
Рассмотрим диаграмму растяжения стержня из малоуглеродистой стали. Пусть круглый стержень длинной l0 и начальным постоянным поперечным сечением площади A0 статически растягивается с обоих торцов силой F.

Диаграмма сжатия стержня имеет вид (рис. 10, а)

где Δl = l — l0 абсолютное удлинение стержня; ε = Δl / l0 — относительное продольное удлинение стержня; σ = F / A0 — нормальное напряжение; E — модуль Юнга; σп — предел пропорциональности; σуп — предел упругости; σт — предел текучести; σв — предел прочности (временное сопротивление); εост — остаточная деформация после снятия внешних нагрузок. Для материалов, не имеющих ярко выраженную площадку текучести, вводят условный предел текучести σ0,2 — напряжение, при котором достигается 0,2% остаточной деформации. При достижении предела прочности в центре стержня возникает локальное утончение его диаметра («шейка»). Дальнейшее абсолютное удлинение стержня идет в зоне шейки ( зона местной текучести). При достижении напряжением предела текучести σт глянцевая поверхность стержня становится немного матовой – на его поверхности появляются микротрещины (линии Людерса-Чернова), направленные под углом 45° к оси стержня.

Расчеты на прочность и жесткость при растяжении и сжатии.
Опасным сечением при растяжении и сжатии называется поперечное сечение бруса, в котором возникает максимальное нормальное напряжение. Допускаемые напряжения вычисляются по формуле:

где σпред — предельное напряжение (σпред = σт — для пластических материалов и σпред = σв — для хрупких материалов); [n] — коэффициент запаса прочности. Для пластических материалов [n] = [nт] = 1,2 … 2,5; для хрупких материалов [n] = [nв] = 2 … 5, а для древесины [n] = 8 ÷ 12.
Расчеты на прочность при растяжении и сжатии.
Целью расчета любой конструкции является использование полученных результатов для оценки пригодности этой конструкции к эксплуатации при минимальном расходе материала, что находит отражение в методах расчета на прочность и жесткость.
Условие прочности стержня при его растяжении (сжатии):

При проектном расчете определяется площадь опасного сечения стержня:

При определении допускаемой нагрузки рассчитывается допускаемая нормальная сила:

Расчет на жесткость при растяжении и сжатии.
Работоспособность стержня определяется его предельной деформацией [ l ]. Абсолютное удлинение стержня должно удовлетворять условию:

Часто дополнительно делают расчет на жесткость отдельных участков стержня.
Следующая важная статья теории:
Изгиб балки
Источник
Если
внешняя сила F
направлена от сечения, то сила N
–положительная, если внешняя сила F
направлена к сечения, то сила N
–отрицательная.
При
решении задач, силу N
будем считать положительной, и направлять
её от сечения. Если при решении задачи,
сила N
будет отрицательной, это означает, что
она направлена к сечении.
Если
продольная сила направлена от сечения,
то брус растянут.
Растяжение считается положительной
деформацией.
Если
продольная сила направлена к сечения,
то брус сжат.
Сжатие считается отрицательной
деформацией.
Изменение
продольный силы по длине бруса удобно
представлять в виде диаграммы, называемой
эпюрой
продольных сил.
Ось
эпюры параллельна продольной силе.
Нулевая линия проводится тонкой линией.
Значения сил откладываются от оси,
вверх – положительные, вниз –
отрицательные. В пределах одного участка
значение силы не меняется, поэтому эпюра
очерчивается отрезками прямых линий,
параллельными оси Oz.
Эпюра
штрихуется тонкими линиями, перпендикулярными
оси. Для наглядности на эпюрах N
и
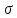 знаками
знаками
« + » и « —» отмечаются положительные и
отрицательные значения участков эпюр.
При
растяжении и сжатии в поперечных сечениях
бруса возникают только нормальные
напряжения, равномерно распределенные
по сечению
и вычисляемые по формуле
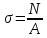 ,
,
где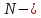 продольная сила;A—
продольная сила;A—
площадь поперечного сечения. Очевидно,
что при растяжении и сжатии форма сечения
на напряжение не влияет.
Во
всех сечениях бруса напряжения
распределены равномерно и что в сечении,
где к брусу приложена вдоль оси
сосредоточенная сила, значения продольной
силы и напряжений меняются скачкообразно.
Пример.
Построить эпюры продольных сил и
нормальных напряжений для ступенчатого
бруса .
Решение.
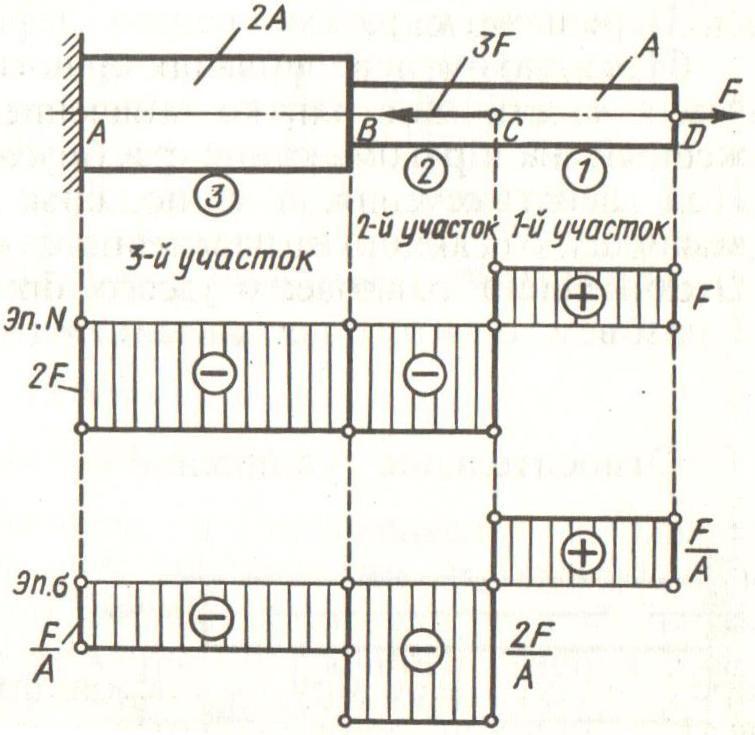
Разобьем
брус на участки и пронумеруем их, как
показано на рисунке.Для
построения эпюры продольных сил N
под рисунком бруса проводим ось эпюры,
параллельную оси бруса, и линиями
ограничиваем его участки.Приступим
к построению эпюры
N.Применяя
метод сечений, устанавливаем, что
во всех поперечных сечениях первого
участка действует продольная си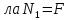 .
.
Откладываем вверх от оси эпюры величину
и произвольном масштабе и проводим
прямую, параллельную оси эпюры. В точке
С
бруса приложена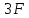 .
.
Применяя метод сечений, устанавливаем,
что во всех поперечных сечениях второго
и третьего участков действуем продольная
сил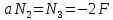 и эпюра N
и эпюра N
будет горизонтальной линией, расположенной
на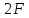 единиц ниже оси эпюры. Очевидно, что
единиц ниже оси эпюры. Очевидно, что
значение ординаты эпюры продольных
сил под заделкой равно реакции заделки.Для
построения эпюры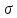 определим нормальные напряжения на
определим нормальные напряжения на
участках бруса, беряотношение
значения продольной силы (из опоры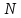 )
)
к площади поперечного сечения. Тогда
на первом участке нормальные напряжения
будут равны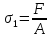 ,
,
на втором —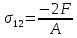 ,
,
на третьем —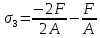 .
.Правила
построения эпюры
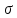 те же, что и для эпюрыN,
те же, что и для эпюрыN,
включая и правило знаков. В пределах
каждою из участков напряжения постоянны,
поэтому эпюра
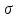 на каждом участке прямая, параллельная
на каждом участке прямая, параллельная
оси.
Перейдем
к рассмотрению деформаций.
Представим
себе прямой брус постоянного поперечного
сечения А,
длиной
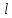 ,
,
жестко защемленный одним концом и
нагруженный на другом конце
растягивающей силой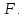 Под действием этой силы брус удлинится
Под действием этой силы брус удлинится
на некоторую величину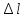 ,
,
которую назовемабсолютным
удлинением.
Отношение
абсолютного удлинения
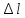 к первоначальной длине
к первоначальной длине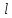 назовемотносительным
назовемотносительным
удлинением
и обозначим
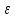 :
:
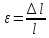

Относительное
удлинение
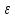
число отвлеченное, иногда его выражают
в процентах: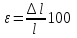
Итак,
деформация бруса при растяжении и сжатии
характеризуется абсолютным и
относительным удлинением или укорочением.
Закон
Гука при растяжении и сжатии
Напряжения
и деформации при растяжении и сжатии
связаны между собой зависимостью,
которая называется законом Гука.
Закон
Гука при растяжении и сжатии справедлив
лишь в определенных
пределах
нагружения и формулируется так: нормальное
напряжение прямо пропорционально
относительному удлинению или укорочению.
Математически
закон Гука можно записан, в виде равенства:
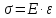
Коэффициент
пропорциональности Е
характеризует
жесткость материала, т. е. его
способность сопротивляться упругим
деформациям растяжения или сжатия, и
называется модулем
продольной упругости или модулем
упругости первого рода.
Модуль
упругости и напряжение выражаются в
одинаковых единицах:
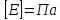 .
.
Значения Е, МПа, для некоторых материалов:
Чугун…..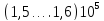 Сталь……(1,96…2,16)
Сталь……(1,96…2,16)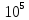
Медь
…..(1.0…1,3) К)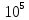 Сплавы алюминия …..(0,69…0,71)
Сплавы алюминия …..(0,69…0,71)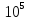
Дерево
(вдоль волокон) ………(0,1 …0,16)
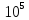
Если
в формулу закона Гука подставим выражения
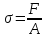 ,
,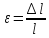
то
получим
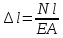 .Эта формула
.Эта формула
называется формулой Гука.
Произведение
ЕА,
стоящее в знаменателе, называется
жесткостью
сечения
при растяжении и сжатии; оно характеризует
одновременно физико-механические
свойства материала и геометрические
размеры поперечного сечения бруса.
Эта
формула читается так: абсолютное
удлинение или укорочение прямо
пропорционально продольной силе, длине
и обратно пропорционально жесткости
сечения бруса.
Отношение
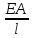 называетсяжесткостью
называетсяжесткостью
бруса при
растяжении или сжатии.
Для
бруса, имеющего несколько участков,
отличающихся материалом, размерами
поперечного сечения, продольной силой,
изменение длины всего бруса равно
алгебраической сумме удлинений и
укорочений отдельных участков:
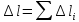 .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Растяжение (сжатие) – это такой вид нагружения стержня, при котором в его поперечном сечении возникает внутренняя продольная сила Ν, действующая вдоль центральной оси z.
Продольная сила Ν – это равнодействующая всех внутренних нормальных сил в сечении. Для вычисления продольной силы применяется метод сечений.

Продольная сила Ν численно равна алгебраической сумме проекций всех сил, действующих по одну сторону от рассматриваемого сечения, на продольную ось бруса.
Правило знаков для продольной силы Ν: при растяжении продольная сила положительна, при сжатии – отрицательна.

График изменения продольных сил по длине стержня называется эпюрой. Эпюра N строится методом сечений на характерных участках бруса. Строится эпюра для использования ее при расчете бруса на прочность. Она дает возможность найти наибольшие значения продольных сил и положение сечений, в которых они возникают.
При растяжении (сжатии) возникают только нормальные напряжения. Согласно гипотезе Я. Бернулли (или гипотеза плоских сечений) в поперечных сечениях, удаленных от места приложения нагрузок, нормальные напряжения распределяются по сечению практически равномерно, а сами сечения, перпендикулярные к оси стержня z, остаются плоскими в процессе нагружения.
Нормальные напряжения в сечении при растяжении (сжатии) вычисляются по формуле

где А – площадь поперечного сечения.
Правило знаков для σ совпадает с правилом знаков для N.
В наклонном сечении, нормаль к которому составляет угол α с осью стержня z,

При растяжении в продольном направлении стержень удлиняется, а его поперечные размеры уменьшаются, при сжатии, напротив, в продольном направлении стержень укорачивается, а его поперечные размеры увеличиваются; Δℓ — абсолютное удлинение или укорочение участка стержня длиной ℓ, Δb – абсолютная поперечная деформация.
Относительное удлинение или укорочение участка стержня длиной ℓ, называемое линейной деформацией, определяется следующим образом
ε=Δℓ/ℓ.
Экспериментально установлено, что в определенной области нагрузок при упругом поведении материала между нормальными напряжениями и линейными деформациями существует линейная зависимость (закон Гука для напряжений)
σ=εЕ,
где Е – модуль продольной упругости или модуль Юнга, это физическая const. Для каждого из материалов величина модуля упругости имеет свое значение:
сталь, Е = 2.105 МПа,
медь, Е = 1.105 МПа,
алюминий, Е = 0,7.105 МПа.
Значение модуля упругости устанавливается экспериментально.
Согласно закону Гука (данную запись называют законом Гука для деформаций)
Δℓ=Νℓ/ЕА
Произведение ЕА – называется жесткостью стержня при растяжении – сжатии.
Перемещение произвольного сечения ступенчатого стержня
w=∑Δℓi
Относительная поперечная деформация:
ε′=Δb/b
где b – поперечный размер стержня.
Эксперименты также показывают, что в упругой стадии деформирования между продольной и поперечной деформациями существует взаимосвязь
μ =│ε′⁄ε│ — const,
где μ — коэффициент Пуассона, берется по модулю ,поскольку у продольной и поперечной деформации разные знаки (при растяжении продольные волокна увеличиваются, а поперечные уменьшаются в размере).
Для твердых материалов имеет значения коэффициент Пуассона
0≤μ ≤0,5
Изменение температуры стержня вызывает его удлинение (при нагревании) или укорочение (при охлаждении)

где — a- коэффициент линейного температурного расширения; Δtº=(tºк-tºн) — изменение температуры между значениями начальным (tºн) и конечным (tºк).
Статически неопределимыми называют системы, имеющие лишние связи – внешние или внутренние.
Для определения внутренних усилий в таких системах недостаточно рассматривать только уравнения равновесия.
В этом случае требуются дополнительные уравнения, число которых равно количеству лишних связей. Дополнительные уравнения составляются на основе анализа картины деформирования системы и использования законов деформирования ее элементов.
Алгоритм решения подобных задач включает следующее:
1) Статическая часть. Составляются уравнения равновесия с включением неизвестных усилий, действующих по направлению лишних связей.
2) Геометрическая часть. Составляются уравнения, описывающие взаимосвязь перемещений характерных точек, удлинений и укорочений отдельных стержней между собой.
3) Физическая связь. Записываются законы деформирования отдельных стержней системы.
Порядок расчета статически неопределимых брусьев
- Задаться направлениями возможных опорных реакций и составить уравнение статики для всей системы в целом.
- Определить степень статической неопределимости и использовать метод сечений с целью выразить неизвестные усилия через неизвестные опорные реакции. При этом неизвестные продольные силы (N) следует предполагать положительными и поэтому направлять «от сечения».
- Сформулировать условие совместности деформаций участков бруса.
- В процессе превращения условия совместности в уравнение совместности деформаций различий в характере деформаций участков не учитывать.
Порядок расчета статически неопределимых шарнирно-стержневых систем
- Задаться направлениями опорных реакций, но уравнений равновесия для всей системы не составлять, а сразу использовать метод сечений и составить уравнения статики для выделенной части системы.
- Определить степень статической неопределимости как разницу между количеством всех неизвестных, оказавшихся в уравнениях статики, и числом самих этих уравнений.
- Рассмотреть (изобразить) любую возможную картину деформаций системы и из ее анализа сформулировать условия совместности деформаций стержней системы (столько, какова степень статической неопределимости).
- В процессе преобразования условий совместности в уравнения совместности деформаций обязательно учитывать различие в характере деформаций стержней (т.е. вводить удлинение со знаком «плюс», а укорочение со знаком «минус») в соответствии с той картиной деформации, которую мы рассматриваем.
Источник
