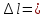Практическая работа тема растяжение и сжатие
Департамент образования города Москвы
ГБПОУ Колледж автоматизации и информационных технологий №20
Техническая механика
Раздел «Сопротивление материалов»
Тема: Растяжение-сжатие
Открытый урок
Практическая работа №9 Проектировочные и проверочные расчеты простых схем соединений
Для студентов специальности 23.02.03 «Техническое обслуживание и ремонт автомобильного транспорта»
Составитель:
Преподаватель общепрофессиональных
дисциплин первой категории
Холмовая Л.М.

Москва 2016
Практическая работа №9 Проектировочные и проверочные расчеты простых схем соединений
Цель: Закрепить теоретические знания по теме «Растяжение-сжатие», приобрести навыки практического применения расчетных формул для определения параметров деформаций простых схем соединения, а также из условия прочности определить размеры поперечного сечения.
Студент должен:
иметь представление о продольных и поперечных деформациях и их связи;
знать:
основные формулы для расчета сил, напряжений и перемещений при растяжении и сжатии;
основные параметры сил, напряжений и перемещений;
уметь производить проектировочные и проверочные расчеты из условия прочности и жесткости.
Технологическая карта занятия
п/п
Наименование перехода
Время,
мин
Приме-чание
1
Приветствие
1
2
Проверка присутствующих
1
3
Объявление темы занятия и хода проведения
3
4
Организация студентов на проведение занятия: пояснения к выполнению практической работы, оформлению и отчету.
5
5
Проверка готовности к выполнению практической работы:
фронтальный опрос по теме «растяжение-сжатие»
8
Вопросы прилагаются
6
Выполнение практической работы:
Порядок выполнения
Выбрать и записать задание по варианту.
Вычертить схему соединения.
Определить нагрузку на стержни.
Выбрать расчетную систему координат.
Составить систему уравнений равновесия для точки крепления груза (т. В):
Решить систему уравнений и определить реакции стержней.
Определить направление реакций и сделать вывод о растяжении или сжатии стержней.
Определить потребную площадь поперечного сечения стержней из условий прочности.
Определить удлинение стержней.
Определить напряжение стержней.
Построить эпюры внутренних сил, напряжений и перемещений для стержней.
Сделать вывод о деформации стержней.
Составить отчет.
Ответить на контрольные вопросы.
Примечание: по мере выполнения работы студенты сдают отчеты о проделанной работе. Работа оценивается преподавателем по пяти бальной системе.
65
7
Подведение итога занятия
4
8
Домашнее задание:
повторить изученный материал (л. 3 стр. 168…181)
отчет по практической работе
рассмотреть материал по теме «Механические испытания» стр. 188…193
3
Итого
90
Вопросы для контроля знаний по теме «растяжение-сжатие» к практической работе «Проектировочные и проверочные расчеты простых схем соединений»
п/п
Вопрос
Ответ
Примеч.
1
Какие силы относятся к внешним силам?
2
Какие деформации вызывают эти силы у элементов конструкций?
3
Какие силы вызывают растяжение или сжатие бруса?
4
Какое обозначение имеют продольные силы внутреннего силового фактора?
5
Какие напряжения действуют при растяжении-сжатии?
6
Какое обозначение имеет нормальное напряжение, как определяется и какова его размерность?
7
Каково условие прочности при растяжении-сжатии?
8
Что обозначает напряжение в квадратных скобках: [σ]?
9
Что характеризует модуль упругости Е?
10
Какова расчетная формула для определения удлинения (укорочения) бруса?
Вопросы и ответы на поставленные вопросы для контроля знаний студентов по теме «растяжение-сжатие»
п/п
Вопрос
Ответ
Примеч.
1
Какие силы относятся к внешним силам?
К внешним силам относятся активные силы и реакции опор
F; G; R
2
Какие деформации вызывают эти силы у элементов конструкций?
Растяжение-сжатие, сдвиг сечения, кручение, изгиб
3
Какие силы вызывают растяжение или сжатие бруса?
Продольные силы – силы, направленные вдоль бруса
4
Какое обозначение имеют продольные силы внутреннего силового фактора?
Продольные силы, внутренний силовой фактор, обозначаются Nz
Н; кН
5
Какие напряжения действуют при растяжении-сжатии?
Нормальное напряжение, обозначение σ
6
Какое обозначение имеет нормальное напряжение, как определяется и какова его размерность?
σ – сигма;

размерность: Н/мм2 (МПа)
Н/м2 (Па)
7
Каково условие прочности при растяжении-сжатии?

МПа
8
Что обозначает напряжение в квадратных скобках: [σ]?
Напряжение в квадратных скобках [σ] – это допускаемое напряжение
9
Что характеризует модуль упругости Е?
Модуль упругости Е характеризует жесткость материала
МПа
10
Какова расчетная формула для определения удлинения (укорочения) бруса?

мм
Практическая работа № 9 Проектировочные и проверочные расчеты простых схем соединений
Цель: Закрепить теоретические знания по теме «Растяжение-сжатие», приобрести навыки практического применения расчетных формул для определения параметров деформаций простых схем соединения, а также из условия прочности определить размеры поперечного сечения.
Содержание:
Основные расчетные формулы.
Выполнение работы:
порядок выполнения работы;
задание для работы;
пример выполнения работы.
Отчет.
Контрольные вопросы.
Литература.
Основные расчетные формулы
Нормальное напряжение: 
где N- продольная сила; А — площадь поперечного сечения.
Удлинение (укорочение) бруса: 
Е -модуль упругости; l — начальная длина стержня.
Допускаемое напряжение: ![]()
[s] — допускаемый запас прочности
Условие прочности при растяжении и сжатии: 
Выполнение работы
Задание: Груз закреплен на стержнях 1 и 2 и находится в равновесии (рис. П6.1). Материал стержней — сталь, допускаемое напряжение [σ] задается; модуль упругости материала Е равно 2· 10 5 МПа. Вес груза F, длина стержней 1 и 2 известны. Определить размеры поперечного сечения и удлинение стержней. Форма поперечного сечения — круг.

Порядок выполнения задания
Выбрать и записать задание по варианту.
Вычертить схему соединения.
Определить нагрузку на стержни.
Выбрать расчетную систему координат.
Составить систему уравнений равновесия для точки крепления груза (т. В).
Решить систему уравнений и определить реакции стержней.
Определить направление реакций и сделать вывод о растяжении или сжатии стержней.
8. Определить потребную площадь поперечного сечения стержней из условий прочности.
9. Определить диаметры стержней 1 и 2.
10. Определить удлинение стержней.
11. Определить напряжение стержней.
12. Выполнить проверочный расчет соединения.
13. Сделать вывод о деформации стержней.
14. Составить отчет.
15. Ответить на контрольные вопросы.
Варианты задания
Вариант
№
Длина стержней, м
Вес груза
α
Допускаемое напряжение
[σ], МПа
1
2
F, кН
1
2,0
1,0
100
30º
120
2
115
3
120
4
125
5
130
6
2,5
1,5
95
45º
140
7
110
8
140
9
145
10
150
11
3,0
2,0
70
60º
160
12
75
13
80
14
85
15
90
16
2,5
1,0
80
60º
120
17
90
18
100
19
115
20
120
21
125
22
130
23
3,5
1,5
95
30º
140
24
110
25
140
26
145
27
150
28
4,0
2,0
70
45º
160
29
75
30
80
31
85
32
90
Пример расчета
Груз закреплен на стержнях и находится в равновесии (рис. П6.1). Материал стержней — сталь, допускаемое напряжение 160 МПа. Вес груза 100 кН. Длина стержней: первого — 2 м, второго — 1 м. Определить размеры поперечного сечения и удлинение стержней. Форма поперечного сечения — круг.

Решение:
1. Определить нагрузку на стержни. Рассмотрим равновесие точки В, определим реакции стержней. По пятой аксиоме статистики (закону действия и противодействия) реакция стержня численно равна нагрузке на стержень.
Наносим реакции связей, действующих в точке В. Освобождаем точку В от связей (рис. П6.1).
Выбираем систему координат так, чтобы одна из осей координат совпала с неизвестной силой (рис. П6.1б).
Составим систему уравнений равновесия для точки В:
![]()
Решаем систему уравнений и определяем реакции стержней.

Направление реакций выбрано, верно. Оба стержня сжаты. Нагрузки на стержни: R1 = 57,4 кН; R2 = 115,5 кН.
2. Определяем потребную площадь поперечного сечения стержней из условий прочности.
Условие прочности на сжатие: ![]()
откуда ![]()
Площадь круга: А = πR2
Стержень 1: (N1 = Rl)
Cтержень 2: (N2 = R2)
![]()
Для круга

Полученные диаметры округляем.
3. Определяем удлинение стержней
Укорочение стержня 1:
![]()

Укорочение стержня 2:

Отчет
Отчет должен содержать:
Наименование и цель практической работы.
Задание по варианту: условие и эскиз нагружения стержней.
Расчеты с пояснениями действий.
Вывод по результатам работы.
К какому виду сопротивления (простому или сложному) относят осевое растяжение (сжатие)?
Какие гипотезы вводят при расчёте на осевое растяжение (сжатие)?
Какие внутренние усилия возникают при осевом растяжении (сжатии) в поперечных сечениях стержня, как обозначаются, какую размерность имеют?
Какие напряжения возникают при осевом растяжении (сжатии) в поперечных сечениях стержня, как обозначаются, какую размерность имеют, по каким формулам определяются?
Какие факторы приводят к возникновению перемещений?
Какие перемещения возникают в случае центрального растяжения (сжатия), как их обозначают, какую размерность они имеют, по каким формулам определяются?
Какие правила знаков вводят для внутренних усилий, напряжений и перемещений при осевом растяжении (сжатии)?
Какие условия прочности используют в осевом растяжении (сжатии)?
Чем отличаются алгоритмы расчёта на прочность для хрупкого и пластичного материалов?
Какие условия жёсткости используют в случае центрального растяжения (сжатия)?
Литература
В.П. Олофинская «Техническая механика», М. ФОРУМ-ИНФРА-М, 2012г.
Раздел 1 Теоретическая механика. Тема 1.2. Плоская система сходящихся сил (стр. 12…27);
Раздел 2 Сопротивление материалов. Тема 2.1. Основные положения. Тема 2.2. Растяжение и сжатие. Продольные и поперечные деформации (стр.162…187)
Практические занятия по разделу «Сопротивление материалов» по теме 2.2. Растяжение и сжатие (стр. 306…308)
Конспекты лекций по темам 1.2.; 2.1. и 2.2.
Интернет-ресурсы.
Источник
Цель:
Для заданного ступенчатого бруса
построить эпюры продольных сил и
нормальных напряжений, определить
удлинение (укорочение) бруса, выполнить
проверочный расчет по прочности.
Задача.
Стальной двухступенчатый брус, длины
ступеней которого указаны на рис.1 (схемы
1-10), нагружен силами F1,
F2и
F3.
Построить эпюры продольных сил и
нормальных напряжений по длине бруса.
Определить перемещение свободного
конца бруса, приняв Е=2ּ105
МПа.
Числовые значения сил F1,
F2
и F3,
площади поперечных сечений ступеней
А1
и А2
для своего варианта взять из таблицы.
Таблица
Вариант | № схемы | F1 | F2 | F3 | А1 | А2 | Вариант | № схемы | F1 | F2 | F3 | А1 | А2 | |||||
кН | см2 | кН | см2 | |||||||||||||||
1 | 2 | 20 | 8 | 14 | 1,2 | 1,8 | 18 | 10 | 19 | 11 | 34 | 1,3 | 0,9 | |||||
2 | 3 | 16 | 25 | 28 | 1,2 | 1,8 | 19 | 9 | 31 | 46 | 20 | 1,9 | 2,5 | |||||
3 | 4 | 26 | 9 | 10 | 1,9 | 1,6 | 20 | 2 | 18 | 10 | 15 | 1,2 | 1,8 | |||||
4 | 6 | 28 | 22 | 12 | 2,8 | 2,6 | 21 | 1 | 16 | 15 | 10 | 1,1 | 1,8 | |||||
5 | 5 | 14 | 16 | 10 | 2,1 | 1,9 | 22 | 4 | 24 | 10 | 8 | 2,0 | 0,7 | |||||
6 | 8 | 10 | 12 | 13 | 0,9 | 0,7 | 23 | 3 | 15 | 24 | 29 | 1,3 | 2,9 | |||||
7 | 7 | 17 | 13 | 6 | 1,1 | 1,5 | 24 | 6 | 26 | 20 | 10 | 2,6 | 2,2 | |||||
8 | 10 | 29 | 2 | 54 | 1,9 | 1,4 | 25 | 5 | 20 | 18 | 12 | 2,5 | 2,2 | |||||
9 | 9 | 40 | 55 | 24 | 2,8 | 3,4 | 26 | 8 | 9 | 11 | 12 | 1,9 | 0,8 | |||||
10 | 2 | 15 | 5 | 13 | 1,0 | 1,2 | 27 | 7 | 14 | 10 | 6 | 1,1 | 1,3 | |||||
11 | 1 | 30 | 10 | 5 | 1,8 | 2,6 | 28 | 10 | 30 | 4 | 56 | 2,0 | 1,5 | |||||
12 | 3 | 8 | 13 | 14,5 | 0,6 | 1,2 | 29 | 9 | 25 | 41 | 18 | 1,6 | 2,1 | |||||
13 | 4 | 16 | 6 | 2 | 1,0 | 0,7 | 30 | 2 | 11 | 6 | 12 | 0,8 | 1,2 | |||||
14 | 6 | 19 | 14 | 4 | 2,4 | 2,1 | 31 | 1 | 17 | 13 | 8 | 1,0 | 2,1 | |||||
15 | 5 | 17 | 19 | 13 | 2,4 | 2,1 | 32 | 3 | 18 | 25 | 7 | 1,5 | 3,2 | |||||
16 | 8 | 17 | 19 | 20 | 1,6 | 1,4 | 33 | 4 | 32 | 17 | 2 | 3,0 | 1,5 | |||||
17 | 7 | 20 | 17 | 10 | 1,3 | 1,9 | 34 | 5 | 19 | 8 | 22 | 2,1 | 1,8 | |||||
Лабораторная работа №2 «Испытание на растяжение образца из низкоуглеродистой стали».
Цель
работы:
Изучение поведения стального образца
при растяжении до разрушения. Определение
величин основных механических
характеристик материала.
Оборудование:
разрывная машина УММ-5, образец.
Порядок выполнения и оформления работы
Изучить
и законспектировать
тип, наименование, принцип действия и
устройство испытательной машины.Зарисовать
эскиз образца до и после испытания.
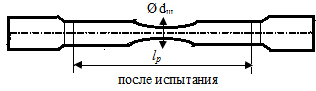
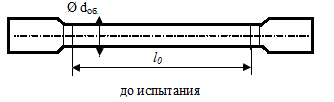
Записать
размеры образца,
данные своего варианта взять из таблицы
1 и схемы и занести в таблицу 2.
Таблица
1. Данные варианта.
Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
№ схемы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Вариант | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
№ схемы | 11 | 12 | 13 | 14 | 15 | 1 | 2 | 3 | 4 | 5 |
Вариант | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
№ схемы | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Таблица
2 Размеры образца
До | После |
Диаметр | Диаметр |
Расчетная | Удлинение |
Площадь | Расчетная |
Площадь |
Вычислить
результаты работы:
Нагрузка,
соответствующая пределу пропорциональности
Fпц=Нагрузка,
соответствующая пределу текучести Fт=Нагрузка,
соответствующая пределу прочности
Fnр=
Результаты
испытаний
Предел
пропорциональности σпц=Предел
текучести σт=Предел
прочности σnр=Относительное
удлинение δ=Относительное
остаточное сужение ψ=
Вывод:
Схема
1
Размеры
образца до испытания:
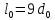 ,
,
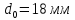 ;
;
Размеры
образца после испытания:
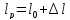 ,
,
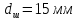 .
.
Масштаб:
по
силе «F»
1 мм=600 Н ,
по
удлинению «
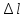 »
»
1 мм=0,005 мм
Схема
2
Размеры
образца до испытания:
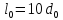 ,
,
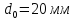 ;
;
Размеры
образца после испытания:
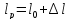 ,
,
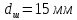 .
.
Масштаб:
по
силе «F»
1 мм=350 Н ,
по
удлинению «
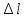 »
»
1 мм=0,02 мм
Схема
3
Размеры
образца до испытания:
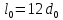 ,
,
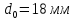 ;
;
Размеры
образца после испытания:
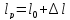 ,
,
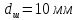 .
.
Масштаб:
по
силе «F»
1 мм=550 Н ,
по
удлинению «
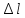 »
»
1 мм=0,0015 мм
Схема
4
Размеры
образца до испытания:
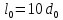 ,
,
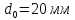 ;
;
Размеры
образца после испытания:
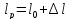 ,
,
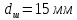 .
.
Масштаб:
по
силе «F»
1 мм=500 Н ,
по
удлинению «
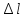 »
»
1 мм=0,0025 мм
Схема
5
Размеры
образца до испытания:
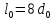 ,
,
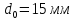 ;
;
Размеры
образца после испытания:
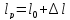 ,
,
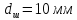 .
.
Масштаб:
по
силе «F»
1 мм=500 Н ,
по
удлинению «
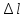 »
»
1 мм=0,004 мм
Схема
6
Размеры
образца до испытания:
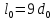 ,
,
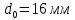 ;
;
Размеры
образца после испытания:
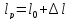 ,
,
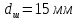 .
.
Масштаб:
по
силе «F»
1 мм=400 Н ,
по
удлинению «
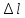 »
»
1 мм=0,0015 мм
Схема
7
Размеры
образца до испытания:
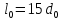 ,
,
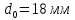 ;
;
Размеры
образца после испытания:
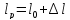 ,
,
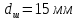 .
.
Масштаб:
по
силе «F»
1 мм=250 Н ,
по
удлинению «
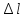 »
»
1 мм=0,005 мм
Схема
8
Размеры
образца до испытания:
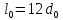 ,
,
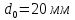 ;
;
Размеры
образца после испытания:
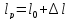 ,
,
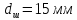 .
.
Масштаб:
по
силе «F»
1 мм=500 Н ,
по
удлинению «
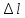 »
»
1 мм=0,003 мм
Схема
9
Размеры
образца до испытания:
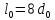 ,
,
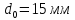 ;
;
Размеры
образца после испытания:
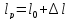 ,
,
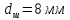 .
.
Масштаб:
по
силе «F»
1 мм=450 Н ,
по
удлинению «
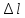 »
»
1 мм=0,002 мм
Схема
10
Размеры
образца до испытания:
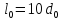 ,
,
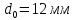 ;
;
Размеры
образца после испытания:
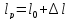 ,
,
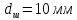 .
.
Масштаб:
по
силе «F»
1 мм=400 Н ,
по
удлинению «
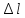 »
»
1 мм=0,002 мм
Схема
11
Размеры
образца до испытания:
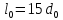 ,
,
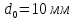 ;
;
Размеры
образца после испытания:
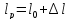 ,
,
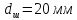 .
.
Масштаб:
по
силе «F»
1 мм=350 Н ,
по
удлинению «
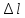 »
»
1 мм=0,003 мм
Схема
12
Размеры
образца до испытания:
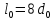 ,
,
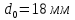 ;
;
Размеры
образца после испытания:
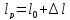 ,
,
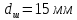 .
.
Масштаб:
по
силе «F»
1 мм=300 Н ,
по
удлинению «
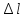 »
»
10 мм=0,0015 мм
Схема
13
Размеры
образца до испытания:
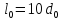 ,
,
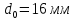 ;
;
Размеры
образца после испытания:
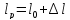 ,
,
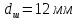 .
.
Масштаб:
по
силе «F»
1 мм=400 Н ,
по
удлинению «
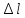 »
»
1 мм=0,0025 мм
Схема
14
Размеры
образца до испытания:
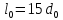 ,
,
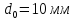 ;
;
Размеры
образца после испытания:
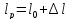 ,
,
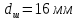 .
.
Масштаб:
по
силе «F»
1 мм=300 Н ,
по
удлинению «
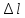 »
»
1 мм=0,003 мм
Схема
15
Размеры
образца до испытания:
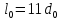 ,
,
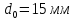 ;
;
Размеры
образца после испытания:
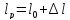 ,
,
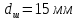 .
.
Масштаб:
по
силе «F»
1 мм=700 Н ,
по
удлинению «
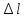 »
»
1 мм=0,002 мм
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Тема: «Растяжение и сжатие»
Цель:
1) закрепитьосновные понятия сопротивления материалов деформация растяжения сжатия;
2) производить расчеты на сжатие;
3) производить расчеты элементов конструкций на прочность;
4) строить эпюры напряжений.
Время выполнения: 8 часов.
Для выполнения задания необходимо знать:
Растяжением или сжатием называется такой вид деформации, при котором в поперечном сечении бруса возникает один ВСФ — продольная сила N. Она равна алгебраической сумме проекций на продольную ось внешних сил, действующих на отсеченную часть бруса:
(23)
Так как величина продольных сил в разных сечениях бруса неодинакова, то строится эпюра продольных сил. Эпюра продольных сил — график, показывающий изменения величины продольных сил в сечении бруса по его длине.
Последовательность построения эпюр продольных сил:
1. Разбиваем брус на участки, ограниченные точками приложения сил (нумерацию участков ведем от незакрепленного конца).
2. Используя метод сечений, определяем величину продольных сил в сечении каждого участка.
3. Выбираем масштаб и строим эпюру продольных сил, т.е. под изображением бруса (или рядом) проводим прямую, параллельную его оси, и от этой прямой проводим перпендикулярные отрезки, соответствующие в выбранном масштабе продольным силам (положительное значение откладываем вверх (или вправо), отрицательное — вниз (или влево)).
Под действием продольных сил в поперечном сечении бруса возникает нормальное напряжение, которое определяется по формуле:
(24)
где
А — площадь поперечного сечения участка.
Гипотеза плоских сечений устанавливает, что при растяжении (сжатии) сечение бруса остается плоским и перпендикулярным линии действия силы. Закон Гука при растяжении — нормальное напряжение, возникающее в поперечных сечениях при растяжении в пределах упругости, прямо пропорционально продольной деформации:
(25)
где
Е — коэффициент пропорциональности, который называется модулем упругости.
Он характеризует жесткость материала, из которого изготовлен элемент конструкции. Для различных материалов его значения определены экспериментально.
Закон Гука для определения деформации растяжения:
(26)
где
— абсолютное изменение продольных размеров;
l0— первоначальные размеры элемента;
ЕА — величина, характеризующая жесткость сечения бруса.
Условие прочности при растяжении: рабочее напряжение должно быть меньше или равно допускаемому напряжению, т.е.
(27)
Используя это условие, можно выполнить три вида расчетов на прочность при растяжении.
1) Проверочный — проверка прочности: по заданной рабочей нагрузке и заданному размеру сечения определяем рабочее напряжение и сравниваем его с допускаемым напряжением. Если — удовлетворяет условию прочности , если — не удовлетворяет условию прочности
2) Проектный — подбор размера сечения по заданной рабочей нагрузке и допускаемому напряжению: (например для вала) —
3) Проверочно-уточненный— определение допускаемого значения рабочей нагрузки по заданному размеру сечения и допускаемому напряжению. (например для круглого бруса):
Задание(подставь и посчитай)
Определение деформации растяжения – сжатия ступенчатого бруса.
Построить эпюры продольных сил и нормальных напряжений для нагруженного стального винта(3) съёмника подшипников (рис. 25). Определить удлинение (укорочение) винта, если Ест= 2 ·105 МПа.
Рисунок 25
Дано: F1 = кН; F2 = кН ; F3 = кН ;
А1= 2 см2 = 2 ·102 мм2 ; А2= 4 см2 = 4 ·102 мм2 ; Ест = 2 ·105 МПа ; l01 = 100 мм ; l02 = 50 мм ; l03 = 200 мм ; l04 = 150 мм
Определить: ∆l
Решение.
1) Определяем продольные силы и строим их эпюру:
2) Определяем величину нормальных напряжений и строим их эпюру:
3) Используя видоизмененный закон Гука, определяем удлинение бруса:
∆l = ∆l1 + ∆l2 + ∆l3 + ∆l4 = мм.
Положительный знак ∆l говорит о том что брус растягивается, отрицательный, что сжимается.
Ответ: ∆l = мм.
Выполните решение задания, взяв данные в таблице 6.
Таблица 6.
| № варианта | Сила F1 , кН | Сила F2 , кН | Сила F3 , кН | № варианта | Сила F1 , кН | Сила F2 , кН | Сила F3 , кН |
Источник