Практическая работа расчеты на прочность при растяжении и сжатии
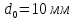
Цель:
Для заданного ступенчатого бруса
построить эпюры продольных сил и
нормальных напряжений, определить
удлинение (укорочение) бруса, выполнить
проверочный расчет по прочности.
Задача.
Стальной двухступенчатый брус, длины
ступеней которого указаны на рис.1 (схемы
1-10), нагружен силами F1,
F2и
F3.
Построить эпюры продольных сил и
нормальных напряжений по длине бруса.
Определить перемещение свободного
конца бруса, приняв Е=2ּ105
МПа.
Числовые значения сил F1,
F2
и F3,
площади поперечных сечений ступеней
А1
и А2
для своего варианта взять из таблицы.
Таблица
Вариант | № схемы | F1 | F2 | F3 | А1 | А2 | Вариант | № схемы | F1 | F2 | F3 | А1 | А2 | |||||
кН | см2 | кН | см2 | |||||||||||||||
1 | 2 | 20 | 8 | 14 | 1,2 | 1,8 | 18 | 10 | 19 | 11 | 34 | 1,3 | 0,9 | |||||
2 | 3 | 16 | 25 | 28 | 1,2 | 1,8 | 19 | 9 | 31 | 46 | 20 | 1,9 | 2,5 | |||||
3 | 4 | 26 | 9 | 10 | 1,9 | 1,6 | 20 | 2 | 18 | 10 | 15 | 1,2 | 1,8 | |||||
4 | 6 | 28 | 22 | 12 | 2,8 | 2,6 | 21 | 1 | 16 | 15 | 10 | 1,1 | 1,8 | |||||
5 | 5 | 14 | 16 | 10 | 2,1 | 1,9 | 22 | 4 | 24 | 10 | 8 | 2,0 | 0,7 | |||||
6 | 8 | 10 | 12 | 13 | 0,9 | 0,7 | 23 | 3 | 15 | 24 | 29 | 1,3 | 2,9 | |||||
7 | 7 | 17 | 13 | 6 | 1,1 | 1,5 | 24 | 6 | 26 | 20 | 10 | 2,6 | 2,2 | |||||
8 | 10 | 29 | 2 | 54 | 1,9 | 1,4 | 25 | 5 | 20 | 18 | 12 | 2,5 | 2,2 | |||||
9 | 9 | 40 | 55 | 24 | 2,8 | 3,4 | 26 | 8 | 9 | 11 | 12 | 1,9 | 0,8 | |||||
10 | 2 | 15 | 5 | 13 | 1,0 | 1,2 | 27 | 7 | 14 | 10 | 6 | 1,1 | 1,3 | |||||
11 | 1 | 30 | 10 | 5 | 1,8 | 2,6 | 28 | 10 | 30 | 4 | 56 | 2,0 | 1,5 | |||||
12 | 3 | 8 | 13 | 14,5 | 0,6 | 1,2 | 29 | 9 | 25 | 41 | 18 | 1,6 | 2,1 | |||||
13 | 4 | 16 | 6 | 2 | 1,0 | 0,7 | 30 | 2 | 11 | 6 | 12 | 0,8 | 1,2 | |||||
14 | 6 | 19 | 14 | 4 | 2,4 | 2,1 | 31 | 1 | 17 | 13 | 8 | 1,0 | 2,1 | |||||
15 | 5 | 17 | 19 | 13 | 2,4 | 2,1 | 32 | 3 | 18 | 25 | 7 | 1,5 | 3,2 | |||||
16 | 8 | 17 | 19 | 20 | 1,6 | 1,4 | 33 | 4 | 32 | 17 | 2 | 3,0 | 1,5 | |||||
17 | 7 | 20 | 17 | 10 | 1,3 | 1,9 | 34 | 5 | 19 | 8 | 22 | 2,1 | 1,8 | |||||
Лабораторная работа №2 «Испытание на растяжение образца из низкоуглеродистой стали».
Цель
работы:
Изучение поведения стального образца
при растяжении до разрушения. Определение
величин основных механических
характеристик материала.
Оборудование:
разрывная машина УММ-5, образец.
Порядок выполнения и оформления работы
Изучить
и законспектировать
тип, наименование, принцип действия и
устройство испытательной машины.Зарисовать
эскиз образца до и после испытания.
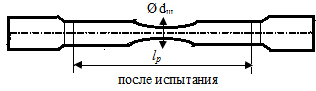
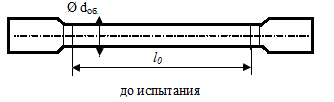
Записать
размеры образца,
данные своего варианта взять из таблицы
1 и схемы и занести в таблицу 2.
Таблица
1. Данные варианта.
Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
№ схемы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Вариант | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
№ схемы | 11 | 12 | 13 | 14 | 15 | 1 | 2 | 3 | 4 | 5 |
Вариант | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
№ схемы | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Таблица
2 Размеры образца
До | После |
Диаметр | Диаметр |
Расчетная | Удлинение |
Площадь | Расчетная |
Площадь |
Вычислить
результаты работы:
Нагрузка,
соответствующая пределу пропорциональности
Fпц=Нагрузка,
соответствующая пределу текучести Fт=Нагрузка,
соответствующая пределу прочности
Fnр=
Результаты
испытаний
Предел
пропорциональности σпц=Предел
текучести σт=Предел
прочности σnр=Относительное
удлинение δ=Относительное
остаточное сужение ψ=
Вывод:
Схема
1
Размеры
образца до испытания:
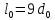 ,
,
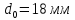 ;
;
Размеры
образца после испытания:
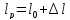 ,
,
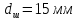 .
.
Масштаб:
по
силе «F»
1 мм=600 Н ,
по
удлинению «
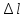 »
»
1 мм=0,005 мм
Схема
2
Размеры
образца до испытания:
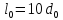 ,
,
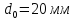 ;
;
Размеры
образца после испытания:
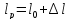 ,
,
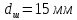 .
.
Масштаб:
по
силе «F»
1 мм=350 Н ,
по
удлинению «
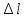 »
»
1 мм=0,02 мм
Схема
3
Размеры
образца до испытания:
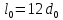 ,
,
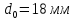 ;
;
Размеры
образца после испытания:
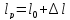 ,
,
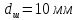 .
.
Масштаб:
по
силе «F»
1 мм=550 Н ,
по
удлинению «
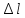 »
»
1 мм=0,0015 мм
Схема
4
Размеры
образца до испытания:
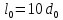 ,
,
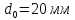 ;
;
Размеры
образца после испытания:
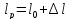 ,
,
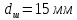 .
.
Масштаб:
по
силе «F»
1 мм=500 Н ,
по
удлинению «
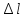 »
»
1 мм=0,0025 мм
Схема
5
Размеры
образца до испытания:
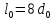 ,
,
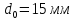 ;
;
Размеры
образца после испытания:
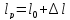 ,
,
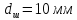 .
.
Масштаб:
по
силе «F»
1 мм=500 Н ,
по
удлинению «
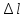 »
»
1 мм=0,004 мм
Схема
6
Размеры
образца до испытания:
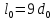 ,
,
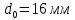 ;
;
Размеры
образца после испытания:
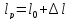 ,
,
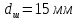 .
.
Масштаб:
по
силе «F»
1 мм=400 Н ,
по
удлинению «
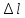 »
»
1 мм=0,0015 мм
Схема
7
Размеры
образца до испытания:
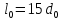 ,
,
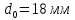 ;
;
Размеры
образца после испытания:
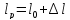 ,
,
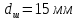 .
.
Масштаб:
по
силе «F»
1 мм=250 Н ,
по
удлинению «
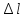 »
»
1 мм=0,005 мм
Схема
8
Размеры
образца до испытания:
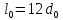 ,
,
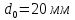 ;
;
Размеры
образца после испытания:
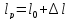 ,
,
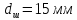 .
.
Масштаб:
по
силе «F»
1 мм=500 Н ,
по
удлинению «
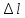 »
»
1 мм=0,003 мм
Схема
9
Размеры
образца до испытания:
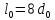 ,
,
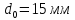 ;
;
Размеры
образца после испытания:
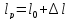 ,
,
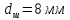 .
.
Масштаб:
по
силе «F»
1 мм=450 Н ,
по
удлинению «
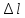 »
»
1 мм=0,002 мм
Схема
10
Размеры
образца до испытания:
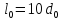 ,
,
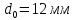 ;
;
Размеры
образца после испытания:
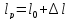 ,
,
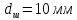 .
.
Масштаб:
по
силе «F»
1 мм=400 Н ,
по
удлинению «
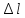 »
»
1 мм=0,002 мм
Схема
11
Размеры
образца до испытания:
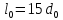 ,
,
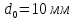 ;
;
Размеры
образца после испытания:
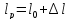 ,
,
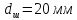 .
.
Масштаб:
по
силе «F»
1 мм=350 Н ,
по
удлинению «
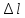 »
»
1 мм=0,003 мм
Схема
12
Размеры
образца до испытания:
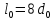 ,
,
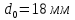 ;
;
Размеры
образца после испытания:
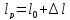 ,
,
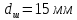 .
.
Масштаб:
по
силе «F»
1 мм=300 Н ,
по
удлинению «
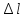 »
»
10 мм=0,0015 мм
Схема
13
Размеры
образца до испытания:
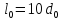 ,
,
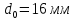 ;
;
Размеры
образца после испытания:
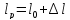 ,
,
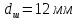 .
.
Масштаб:
по
силе «F»
1 мм=400 Н ,
по
удлинению «
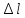 »
»
1 мм=0,0025 мм
Схема
14
Размеры
образца до испытания:
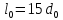 ,
,
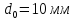 ;
;
Размеры
образца после испытания:
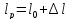 ,
,
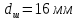 .
.
Масштаб:
по
силе «F»
1 мм=300 Н ,
по
удлинению «
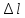 »
»
1 мм=0,003 мм
Схема
15
Размеры
образца до испытания:
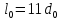 ,
,
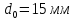 ;
;
Размеры
образца после испытания:
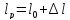 ,
,
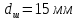 .
.
Масштаб:
по
силе «F»
1 мм=700 Н ,
по
удлинению «
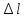 »
»
1 мм=0,002 мм
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Задание
Для конструкции
и эпюры внутренних сил, построенных при
выполнении практической работы № 5,
материал – бронза, [σ] = 70 МПа, запас
прочности [s] = 1,5.
Установить опасное
сечение бруса и записать условие
прочности.Определить размеры
постоянного поперечного сечения бруса
в форме квадрата, круга, прямоугольника,
приняв h/b=2,0;
Цель работы
–
научиться проводить проектировочные
и проверочные расчеты на прочность
и жесткость при
растяжении и сжатии.
Теоретическое
обоснование
Основные типы
расчетов на прочность
Используя условие
прочности (5.3), можно решать следующие
основные типы расчетов:
Проектировочный
расчет:
— определение по
известной нагрузке и допускаемому
напряжению размеров поперечного сечения
стержня
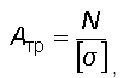
(6.1)
— подбор материала
![]()
(6.2)
где
A![]() —
—
требуемая площадь сечения;
N
– продольная сила;
[s]- допускаемый
коэффициент запаса прочности;
![]() —
—
допускаемое напряжение.
Проверочный
расчет
— проверка прочности
стержня, т.е. определение по заданным
нагрузке и размерам поперечного сечения
стержня фактических напряжений и
сравнение их с допускаемыми.
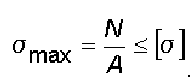
(6.3)
Определение
максимальной нагрузки
по заданным размерам поперечного сечения
и [s]
![]()
(6.4)
Величина деформации
стержня ∆L
при растяжении или сжатии находится по
формуле
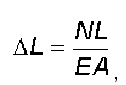
(6.5)
где L – длина
стержня до нагружения;
N – продольная
сила;
Е – модуль
упругости при растяжении, сжатии;
А – площадь
поперечного сечения стержня.
Условие жесткости
при растяжении и сжатии
![]()
(6.6)
где L – продольная
деформация стержня;
[L]
– допускаемая деформация.
Наиболее
рациональным следует признать сечение,
обладающее минимальной площадью при
заданной нагрузке на брус. В этом случае
расход материала на изготовление бруса,
будет минимальным. Для получения бруса
минимальной материалоемкости нужно
стремиться к тому, чтобы по возможности
наибольший объем материала работал при
напряжениях, равных допускаемым или
близким к ним. Прежде всего рациональное
сечение бруса должно удовлетворять
условию
равнопрочности растянутой и сжатой зон
бруса.
Иными словами необходимо, чтобы наибольшие
напряжения растяжения (max
![]() )
)
наибольшие напряжения сжатия (max
![]() )
)
одновременно достигали допускаемых
напряжений
![]() и
и
![]() .
.
Порядок
выполнения работы
С помощью метода
сечений по виду и расположению нагрузок,
устанавливают вид внутренних силовых
факторов, возникающих в поперечных
сечениях бруса, и делают вывод о виде
нагружения бруса.С помощью метода
сечений определяют значение и знак ВСФ
во всех сечениях по длине бруса, строят
их эпюры и отыскивают опасное сечение
бруса.По виду ВСФ
устанавливают вид напряжения, возникающего
в точках опасного сечения. Расчетное
напряжение (максимальное напряжение
в опасной точке опасного сечения бруса)
определяют как отношение ВСФ к поперечному
размеру.Определяют размеры
поперечных сечений.Ответить на
контрольные вопросы.
Контрольные
вопросы
Какие внутренние
силовые факторы возникают в сечении
бруса при растяжении и сжатии?Как распределяются
по сечению силы упругости при растяжении
и сжатии?Какого характера
напряжения возникают в поперечном
сечении при растяжении и сжатии:
нормальные или касательные?Как распределены
напряжения по сечению при растяжении
и сжатии?Запишите формулы
для расчета нормальных напряжений при
растяжении и сжатии.Перечислите
характеристики прочности.В чем различие
между предельным и допускаемым
напряжениями?Запишите условие
прочности при растяжении и сжатии.
Отличаются ли условия прочности при
расчете прочности на растяжение и
расчете на сжатие?
Пример выполнения
В заданном брусе
два участка 1 и 2. Так как силы нагружающие
брус, расположены по его центральной
продольной оси, то в поперечных сечениях
возникает лишь один внутренний силовой
фактор – продольная сила N,
т. е. имеет место растяжение (сжатие)
бруса.Сечение будет
опасным, если напряженность σ будет
наибольшей (без учета знака). По эпюре
(г), видно, что опасное сечение 4 или 2,
где
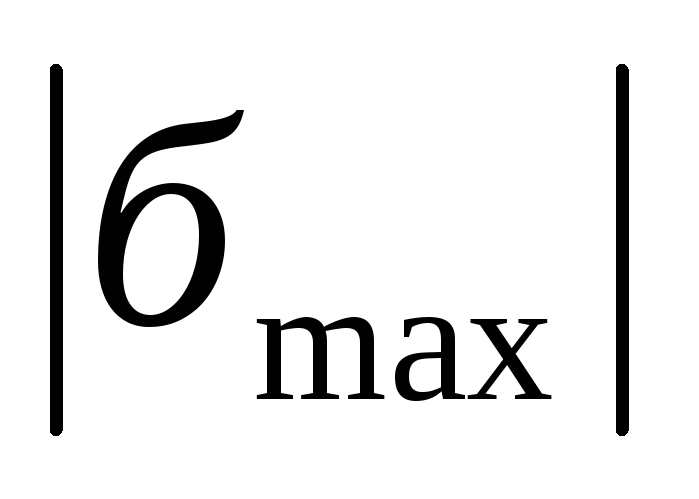 .
.Запишем условие
прочности:
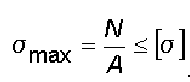
σ![]()
=
![]() ;
;
![]() ≤
≤
[σ]
Определяем
коэффициент запаса прочности:
[s]![]()
=
![]() >
>
1,5; [s]![]()
=
![]() >
>
1,5
Прочность бруса
обеспечена, однако со значительной
(более 25%) недогрузкой, что недопустимо
из-за перерасхода материала. Из условия
прочности определим новые рациональные
размеры сечения каждого из участков
бруса:
![]() ;
;
![]()
Определяем размеры
поперечного сечения бруса:
квадрат – а
=
![]()
круг –
![]()
, округляем до d = 12,0 мм
прямоугольник
—
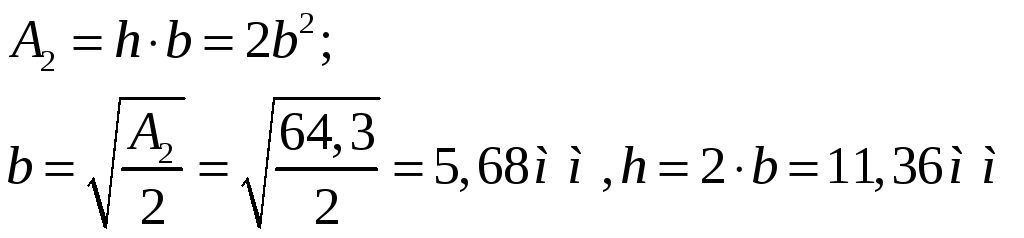
округляем b =
6,0 мм, h = 11,5 мм
Аналогичные
расчеты проводят для участка 4
Проводим проверочный
расчет:
![]()
— прочность
обеспечена
Аналогичный
расчет проводим для участка 4
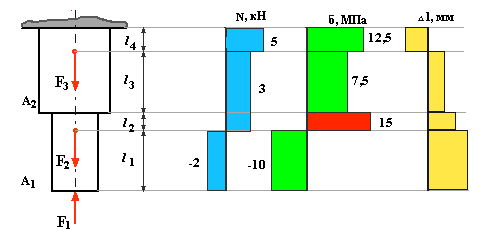
а
б в
г
Рис.6.1
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Государственное автономное профессиональное образовательное учреждение «Кузбасский техникум архитектуры, геодезии и строительства»
ГАПОУ КузТАГиС

ТЕХНИЧЕСКАЯ МЕХАНИКА
Методические рекомендации
по выполнению самостоятельной расчетно-графической
работы №1 Расчет на прочность при растяжении — сжатии
для студентов очной формы обучения специальности
07.02.01 «Архитектура»
Кемерово, 2015
Белоусова Надежда Борисовна
Техническая механика [Текст]: Методические рекомендации по выполнению расчетно-графической работы № 1 «Расчет на прочность при растяжении-сжатии» для студентов очной формы обучения специальности 07.02.01 «Архитектура»/авт. сост. Н.Б.Белоусова – Кемерово, 2015. 17с.
Методические рекомендации содержит общие понятия, правила знаков, особенности и порядок построения эпюр внутренних усилий. Приведены примеры построения эпюр.
Методически рекомендации предназначены для студентов очной формы обучения специальности 07.02.01 «Архитектура».
ОДОБРЕНО
ЦМК отделения «Дизайн» и «Архитектура»
Протокол №___ от _______________
Председатель____________________Ражева Г.Н.
УТВЕРЖДЕНО
Заместитель директора
По учебной работе________________Н.В.Мишенина
Введение
Любое инженерное сооружение – здание, мост и др. помимо элементов, обеспечивающих функциональное назначение данного объекта, обязательно имеет несущие элементы конструкции, составляющие «силовой каркас» и предназначены для восприятия нагрузок.
Несущие элементы конструкции должны проектироваться и создаваться так, чтобы они были прочными и долговечными.
Изучение дисциплины «Техническая механика» дает обучающимся комплекс знаний, умений и навыков для выполнения несложных расчетов элементов конструкций на растяжение-сжатие, изгиб и сложные виды деформаций.
Цели работы:
Обучающая — освоить последовательность построения эпюр продольных сил;
Развивающая – способствовать развитию мышления, умению анализировать;
Воспитательная – понимать сущность и социальную значимость своей будущей профессии;
Формировать умение ответственно и качественно выполнять профессиональные функции;
Задачи:
Научить определять продольные внутренние усилия
Изучить правила и последовательность построения эпюр
В результате выполнения практических работ обучающиеся осваивают следующие общие и профессиональные компетенции: ОК 1 – ОК 9;
ПК 1.1 — Разрабатывать проектную документацию объектов различного назначения;
ПК 2.1 — Участвовать в авторском надзоре при выполнении строительных работ в соответствии с разработанным объемно-планировочным решением;
ПК 2.2 — Осуществлять корректировку проектной документации по замечаниям смежных и контролирующих организаций и заказчика;
1.Общие понятия и основные формулы при растяжении (сжатии)
Растяжением (сжатием) называют такой вид деформации, при котором в прямолинейных стержнях возникают только продольные силы. На растяжение (сжатие) работают тяги, канаты, колонны, элементы стержневых систем (фермы). Внутреннее усилие, нормальное к плоскости поперечного сечения и проходящее через его центр тяжести, называется продольными обозначается через N.
Растягивающие продольные силы (направлены от сечения) принято считать положительными, а сжимающие (направлены к сечению) – отрицательными. 
Рис.1.1
Продольное усилие Nположительно, если оно направлено от сечения (рис.1.1 а) и отрицательно, если направлено к сечению (рис.1.1 б).
Нормальные напряжения в поперечных сечениях определяются по формуле:
Ϭ =
гдеϬ – нормальное напряжение (Па);
N – продольная сила (Н);
А — площадь поперечного сечения, м2;
Изменение длины стержня при растяжении (сжатии) называется абсолютной продольной деформацией и обозначается символом ΔƖ.
Отношение абсолютной продольной деформации к первоначальной длине стержня называется относительной продольной деформацией (. =
Физическая сторона явлений, происходящих при растяжении (сжатии), изучается на опытах. Отметим основные их результаты:
Пока напряжение в материале стержня не достигло определенного предела, стержень остается абсолютно упругим, т.е. при снятии нагрузки в нем исчезают все деформации.
В упругом стержне отношение нормальных напряжений к относительным деформациям есть величина постоянная для каждого вида материала и называется модулем упругости материала(Е)
Е =
А зависимость Ϭ = Е × называется «законом Гука»
Несущая способность стержня оценивается условием прочности
Ϭ = ≤ R
ПРИМЕР РАСЧЕТА КОНСТРУКЦИИ, РАБОТАЮЩЕЙ НА РАСТЯЖЕНИЕ-СЖАТИЕ
Для заданной колонны из бетона (рис.1.3,ɑ):
определить значения расчетных нагрузок;
определить продольные силы и построить эпюру продольных сил;
из условия прочности определить площадь поперечного сечения колонны сплошного сечения;
определить площади поперечных сечений колонны по участкам в соответствии с эпюрой Nи сравнить объем полученной ступенчатой колонны с колонной постоянного сечения;
Построить эпюру напряжений ступенчатой колонны и проверить выполнение условия прочности;
Принять: Rсж. = 10 МПа; Rраст. =1,2 МПа
nр=1,25; nq = 1,11;
qн =90 кН/м; Рн = 200 кН;
Решение
Определяем значения расчетных нагрузок
Р = Рн х nр = 200 · 1,25= 250 кН;
q = qн х nq
где Рн, qн-нормативные нагрузки;
nр, nq–коэффициенты надежности по нагрузке;
Р, q-расчетные нагрузки;
Определим продольные силы в поперечных сечениях колонны на рис. 1.3, а. По длине колонны можно выделить четыре участка. На каждом участке намечаем произвольные сечения и фиксируем их координатами x:
0 ≤ x1 ≥ 1,0; 0 ≤ x2 ≥ 1,5;
0 ≤ x3 ≥ 1,5; 0 ≤ x4 ≥ 2,0;
Записываем уравнения и определяем продольные силы на каждом участке.
N1 = — Р1 – q1 · x1 = — 250 – 100 · x1
при x1 = 0,N1= -250 кН;
при x1 = 1,0,N1= -350 кН;
N2 = — Р1 – Р2 — q1(1,0 + x2) = — 750 – 100(1,0 + x2) ;
при x2 = 0,N2= — 850 кН;
при x2 = 1,5,N2= — 1000 кН;
N3 = — Р1 – Р2 – Р3 — q1(2,5 + x3) = — 1250 – 100(2,5 + x3) ;
при x3 = 0,N3= — 1250 кН;
при x3 = 1,5,N3= — 1400 кН;
N4 = — Р1 – Р2 – Р3 + Р4 — q1(4 + x3) = 300 – 100(4 + x3) ;
при x4 = 0,N4= 300 кН;
при x4 = 1,5,N4= 100 кН;
Эпюра N показана на рис.1.3,в
Проектируем колонну в двух вариантах: колонна постоянного сечения и ступенчатая колонна.
— Колонна постоянного сечения
Находим требуемую площадь поперечного сечения из условия прочности при сжатии:
Ϭ = ≤ Rсж., Rсж. = 10 МПа
Наибольшее значение продольной силы в колонне |Nсж.| = 1400 кН
|1400·103|
= 0,14 м2
10·106
Из условия прочности при растяжении :
Ϭ = ≤ Rраст., Rраст. = 1,2 Мпа
300·103
= 0,25 м2
1,2·106
Требуемая площадь из условия прочности при растяжении больше, чем при сжатии, поэтому принимаем А=0,25 м2
— Ступенчатая колонна
Находим площади поперечных сечений участков:
тупенчатая колонна показана на рис. 1.3, г
Объем колонны постоянного сечения V1 = 6 х 0,25 = 1,5м3
Объем ступенчатой колонны V2=1,0х0,035 +1,5х0,1+1,5х0,14+2х0,25= 0,895м3
V1
=
1,5
=1,68 м3
V2
0,895
Т.е. по материалу ступенчатая колонна экономичнее на 60 %
рис. 1.3
Дальнейший расчет относится к ступенчатой колонне
Строим эпюру Ϭ
Участок 1 (АВ)
ϬА = — = — 7,14 МПа; ϬВ = — = — 10 МПа;
Участок 2 (ВС)
ϬВ = — = — 8,5 МПа; ϬС = — = — 10 МПа;
Участок 3 (СD)
ϬС = — = — 8,93 МПа; ϬD = — = — 10 МПа;
Участок 4 (DF)
ϬD = = 1,2 МПа; ϬF = = 0,4 МПа;
Эпюра Ϭ показана на рис. 1.4, б
Вывод: на эпюре Ϭ нет значений ординат, превышающих значения расчетных сопротивлений материала на растяжение и сжатие, т.е. по всем сечениям выполняется условие прочности.
3. Критерии оценки самостоятельной работы
оценка 5 (отлично) – при выполнении работы продемонстрированы знания основных теоретических концепций, решение выполнено в соответствии с требованиями и соблюдением определенной последовательности с аккуратно вычерченными эпюрами;
оценка 4 (хорошо) – при выполнении работы недостаточно продемонстрированы знания основных теоретических концепций, решение выполнено в соответствии с требованиями и соблюдением определенной последовательности с аккуратно вычерченными эпюрами;
оценка 3 (удовлетворительно– при выполнении работы недостаточно продемонстрированы знания основных теоретических концепций, решение выполнено не в соответствии с требованиями, не соблюдена последовательность решения, неаккуратно вычерчены эпюры;
оценка 2 (неудовлетворительно) – при выполнении работы не продемонстрированы знания основных теоретических концепций, решение выполнено не в соответствии с требованиями, не соблюдена последовательность решения, неправильно построены эпюры;

рис. 1.4
Задание на выполнение расчетно-графической работы №1
Для заданной колонны, выполненной из бетона:
Определить значения расчетных нагрузок;
Определить продольные силы и построить эпюру продольных сил
Из условия прочности запроектировать колонну в двух вариантах:
Колонну постоянного сечения по наибольшей продольной силе (растягивающей или сжимающей);
Ступенчатую колонну в соответствии с эпюрой N;
Для ступенчатой колонны:
Построить эпюры напряжений;
Принять: R сж.= 10 Мпа; R раст.= 1,2 Мпа;
n q = 1.1; n p = 1.2
Варианты заданий
Номер
варианта
1
2
3
4
5
6
7
8
9
ɑ (м)
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
b (м)
1,5
1,6
1,7
1,8
1,9
1,1
1,2
1,3
1,4
c (м)
1,9
1,8
1,7
1,6
1,5
1,4
1,3
1,2
1,1
Р (Кн)
110
120
130
140
150
160
170
180
190
q (Кн/м)
90
85
80
75
70
65
60
55
60
Номер
варианта
10
11
12
13
14
15
16
17
18
ɑ (м)
2,0
1,9
1,8
1,7
1,6
1,5
1,4
1,3
1,2
b (м)
1,5
1,6
1,7
1,8
1,9
2,0
1,2
1,3
1,4
c (м)
1,4
1,3
1,2
1,5
1,4
1,6
1,7
1,8
1,5
Р (Кн)
210
215
220
225
230
235
240
245
250
q (Кн/м)
100
105
110
115
100
105
110
115
50
Номер
варианта
19
20
21
22
23
24
25
26
27
ɑ (м)
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8