Построить эпюру нормального напряжения при растяжении и сжатии

Построение эпюр продольных сил – это решение статически определимой задачи. Производится для выявления картины нагрузки упругого тела. Вернее, уточнения ее схематизации.
Необходимо для определения наиболее напряженного, так называемого «опасного» сечения. Затем методами сопромата (сопротивления материалов) проводится анализ с прогнозированием перемещений элементов конструкции.
Но всему свое время. Сначала немного о терминах.
Основные понятия
Брусом (балкой) называют тело, вытянутое вдоль оси. То есть длина преобладает над шириной и высотой.

Если имеются только осевые (продольные) силы, то объект подвергается растяжению/сжатию. В этом случае в материале возникают только нормальные поперечному сечению силы противодействия и тело считают стержнем.
Статическая определимость подразумевает достаточность схемы для установления внутренних усилий противодействия. Участок – часть балки с неизменным сечением и характерной нагрузкой.
Правила построения учитывают знаки усилий. Растягивающие принимают положительными, сжимающие – отрицательными.
В системе СИ силы измеряются в ньютонах (Н). Длины в метрах (м).
Что такое эпюра продольных сил
Показывает, какой силой (в нашем предположении нормальной) загружен каждый участок. По всей длине стержня. Иначе говоря, эпюра – наглядное графическое изображение изменения нагрузки по всей длине конструкции.
Как построить эпюру продольных сил
Используется метод сечений. Балка виртуально рассекается на каждом участке и ищется противодействующая N. Ведь задача статическая.
Сопротивление рассчитывается по формуле:
где:
Fl – действующие на участке l силы (Н);
ql – распределенные нагрузки (Н/м).
Порядок построения:
1. Рисуется схема балки и механизмов закрепления;
2. Производится разделение на участки;
3. Для каждого рассчитывается N с учетом знаков. Если у балки есть незакрепленный конец, то начинать удобнее именно с него. В противном случае считается реакция опор. И оптимальнее выбирать сечение с меньшим количеством действующих факторов:
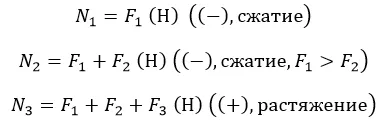
Нетрудно заметить, что последнее уравнение дает еще и реакцию опоры;
4. Параллельно оси стержня намечается база эпюры. Положительные значения масштабировано проставляются выше, отрицательные – ниже. Эпюру наглядно совмещать с расчетной схемой. Итоговый результат и промежуточные сечения показаны на рис. 1.
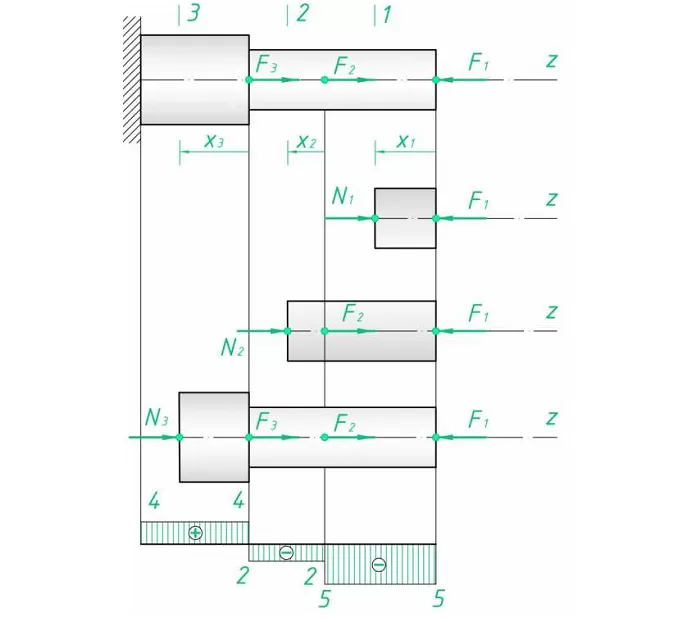
Рис. 1. Эпюра продольных сил
Рассмотрим случай:
F1 = 5 (кН);
F2 = 3 (кН);
F3 = 6 (кН).
Вычислим:
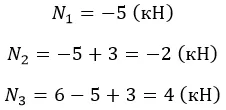
Проверить эпюру можно по скачкам: изменения происходят в точках приложения сил на их величину.
Пример построения эпюр и решения задач
Построить эпюру сил для следующего случая (рис. 2):
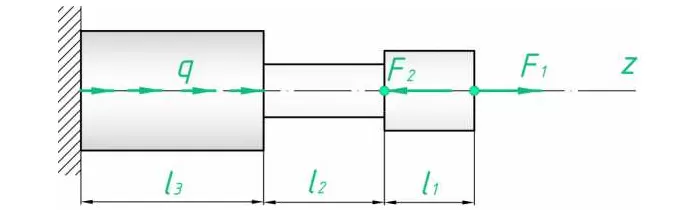
Рис. 2
Дано:
Решение.
Разбиение на участке вполне очевидно. Найдем сопротивление на выделенных:
Распределенная нагрузка зависит от длины, на которой приложена. Поскольку нарастает линейно, значение N2 будет постепенно увеличиваться/уменьшаться в зависимости от знака q.
Эпюра такого вида усилия представляет собой прямоугольный треугольник с катетами l3 и ql3 (в масштабе). Поскольку распределение линейно.
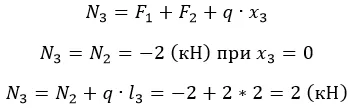
По полученным данным строим эпюру (рис. 3).
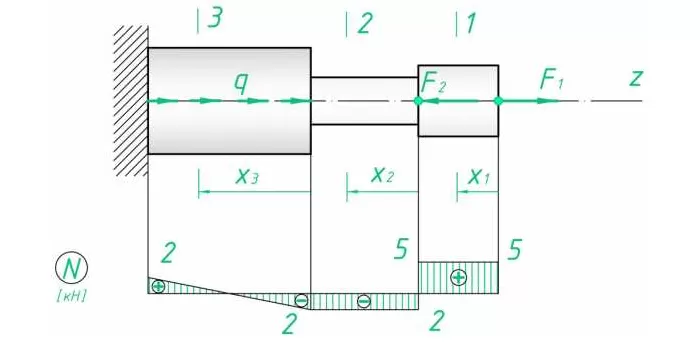
Рис. 3
Заключение
Приведенный алгоритм является предварительным этапом в расчете модели на прочность. «Слабое» место находится уже с учетом площади поперечного сечения.
В сети имеются онлайн сервисы для помощи в расчетах при вычерчивании. Но стоит ли ими пользоваться, если процедура настолько проста? Если не запутаться в знаках, конечно. Это самая распространенная ошибка.
Источник
1. На рисунке проводиться ось ОХ, совпадающая с продольной осью стержня.
2. Под рисунком стержня проводятся две базовые нулевые линии, параллельно продольной оси стержня. Одна для эпюры продольной силы Nz
Вторая базовая нулевая линия для эпюры нормальных напряжений (Мпа).
3. Стержень разбивается на участки. Для границ участков проводятся вертикальные линии в точках приложения нагрузки и изменения площади поперечного сечения вниз до пересечения с базовыми нулевыми линиями. Нумерация участков начинается со свободной стороны стержня для задачи статически определимой. Если задача статически неопределимая, то нумерация выполняется слева направо.
4. Для определения значения продольной силы используется метод сечений. В середине участка проводится сечение. Указывается направление продольной силы. Положительным считается направление продольной силы, направленной от сечения (растягивает). Значение продольной силы Nz определяется из условия равновесия отсечённой части (сумма проекций на ось ох всех действующих сил равна нулю 0).
5. Вычисляем значение нормальных напряжений.
6. Положительные значения продольной силы и нормального напряжения откладываем вверх от базовой нулевой линии, отрицательные вниз.
7. Проверяем правильность решения задачи по эпюре продольной силы. В точках, где приложена сосредоточенная сила, на эпюре должен быть скачок равный значению продольной силы.
8. Условие прочности проверяем по эпюре нормальных напряжений. Максимальные напряжения, возникающие в конструкции, не должны превышать допускаемых.
Пример №1: Построить эпюры продольной силы N и нормального напряжения σ, проверить на прочность стальной стержень, закрепленный с одной стороны (статически определимая задача). Р1 = 10кН Р2 = 15кН
Р3 =15кН
=100 Мпа; А1 = F; А2 = 2F; F = 100 мм2
Решение:
Параллельно продольной оси стержня проводим две базовые нулевые линии для продольной силы и нормального напряжения.
Разбиваем стержень на участки, начиная со свободной стороны. Проводим вниз вертикальные линии в точках приложения сил и изменения площади поперечного сечения до пересечения с нулевыми линиями. Нумерация участков начинается со свободной стороны стержня.
1 участок:
— на первом участке проводим сечение, перпендикулярное продольной оси, мысленно отбрасываем большую часть и рассматриваем меньшую часть стержня. Заменяем действие отброшенной части на оставленную продольной силой N1. Положительным считается действие от сечения (растягивает).
Рассматриваем равновесие оставленной части, проецируя действующие силы на ось ОХ:
Определяем продольную силу на первом участке:
-N1+ Р1=0 следовательно N1 = Р1=10 кН
Определяем нормальное напряжение на первом участке
2 участок:
-N2+ Р1 — Р2=0 следовательно N2 = Р1-Р2 =10-15= -5 кН
3 участок:
-N3+ Р1 — Р2=0 следовательно N3 = Р1-Р2 =10-15= -5 кН
4 участок:
-N4+ Р1 — Р2+Р3=0 следовательно N4 = Р1-Р2+Р3=10-15+15= 10 кН
Рис. 10.
Метод сечений для определения продольной силы.
Для построения эпюр продольной силы и нормального напряжения задаёмся произвольным масштабом (например: одна клеточка -5 кН и -25 мегапаскалей). Строим эпюры продольной силы и нормального напряжения, откладывая положительные значения вверх от базовой нулевой линии, отрицательные вниз.
Проверяем правильность решения задачи по эпюре продольной силы, в точке приложения сосредоточенной силы на эпюре должен быть скачок, равный действующей силе.
По эпюре нормального напряжения проверяем условие прочности максимальные напряжения должны быть меньше или равны допустимым, значит прочность обеспечена.
Рис.11.
Эпюры продольной силы N и нормального напряжения σ.
СПИСОК ЛИТЕРАТУРЫ
1. Рубашкин А.Г. Лабораторные работы по сопротивлению материалов.- М.: Высшая школа, 1961.-159с.
2. Афанасьев A.M., Марьин В.А. Лабораторный практикум по сопротивлению материалов.- М.: Наука, 1975.-284с.
3. Феодосьев В.И. Сопротивление материалов.- М.: Наука, 1979.-559с.
4. Писаренко Г.С. Сопротивление материалов.- Киев.: Высшая школа, 1973.-667с.
Источник
Внутренние усилия при растяжении-сжатии.
Осевое (центральное) растяжение или сжатие прямого бруса вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса. При растяжении или сжатии в поперечных сечениях бруса возникают только продольные силы N. Продольная сила N в некотором сечении равна алгебраической сумме проекции на ось стержня всех внешних сил, действующих по одну сторону от рассматриваемого сечения. По правилу знаков продольной силы N принято считать, что от растягивающих внешних нагрузок возникают положительные продольные силы N, а от сжимающих — продольные силы N отрицательны (рис. 5).

Чтобы выявить участки стержня или его сечения, где продольная сила имеет наибольшее значение, строят эпюру продольных сил, применяя метод сечений, подробно рассмотренный в статье:
Анализ внутренних силовых факторов в статистически определимых системах
Ещё настоятельно рекомендую взглянуть на статью:
Расчёт статистически определимого бруса
Если разберёте теорию в данной статье и задачи по ссылкам, то станете гуру в теме «Растяжение-сжатие» =)
Напряжения при растяжении-сжатии.
Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:
где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.
Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:
Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.
Деформации при растяжении-сжатии.
Рассмотрим деформации, возникающие при растяжении (сжатии) стержня (рис.6, а). Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l1 и его длины до деформации l
Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением, или относительной продольной деформацией:
При растяжении продольная деформация положительна, а при сжатии – отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:
где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).
Таблица 1
Модуль продольной упругости для различных материалов

Абсолютная поперечная деформация бруса равна разности размеров поперечного сечения после и до деформации:
Соответственно, относительную поперечную деформацию определяют по формуле:
При растяжении размеры поперечного сечения бруса уменьшаются, и ε’ имеет отрицательное значение. Опытом установлено, что в пределах действия закона Гука при растяжении бруса поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε’ к продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона μ:
Экспериментально установлено, что на упругой стадии нагружения любого материала значение μ = const и для различных материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5 (табл. 2).
Таблица 2
Коэффициент Пуассона.

Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N:
Данной формулой можно пользоваться для вычисления абсолютного удлинения участка стержня длиной l при условии, что в пределах этого участка значение продольной силы постоянно. В случае, когда продольная сила N изменяется в пределах участка стержня, Δl определяют интегрированием в пределах этого участка:
Произведение (Е·А) называют жесткостью сечения стержня при растяжении (сжатии).
Механические свойства материалов.
Основными механическими свойствами материалов при их деформации являются прочность, пластичность, хрупкость, упругость и твердость.
Прочность — способность материала сопротивляться воздействию внешних сил, не разрушаясь и без появления остаточных деформаций.
Пластичность – свойство материала выдерживать без разрушения большие остаточные деформации. Неисчезающие после снятия внешних нагрузок деформации называются пластическими.
Хрупкость – свойство материала разрушаться при очень малых остаточных деформациях (например, чугун, бетон, стекло).
Идеальная упругость – свойство материала (тела) полностью восстанавливать свою форму и размеры после устранения причин, вызвавших деформацию.
Твердость – свойство материала сопротивляться проникновению в него других тел.
Рассмотрим диаграмму растяжения стержня из малоуглеродистой стали. Пусть круглый стержень длинной l0 и начальным постоянным поперечным сечением площади A0 статически растягивается с обоих торцов силой F.

Диаграмма сжатия стержня имеет вид (рис. 10, а)

где Δl = l — l0 абсолютное удлинение стержня; ε = Δl / l0 — относительное продольное удлинение стержня; σ = F / A0 — нормальное напряжение; E — модуль Юнга; σп — предел пропорциональности; σуп — предел упругости; σт — предел текучести; σв — предел прочности (временное сопротивление); εост — остаточная деформация после снятия внешних нагрузок. Для материалов, не имеющих ярко выраженную площадку текучести, вводят условный предел текучести σ0,2 — напряжение, при котором достигается 0,2% остаточной деформации. При достижении предела прочности в центре стержня возникает локальное утончение его диаметра («шейка»). Дальнейшее абсолютное удлинение стержня идет в зоне шейки ( зона местной текучести). При достижении напряжением предела текучести σт глянцевая поверхность стержня становится немного матовой – на его поверхности появляются микротрещины (линии Людерса-Чернова), направленные под углом 45° к оси стержня.

Расчеты на прочность и жесткость при растяжении и сжатии.
Опасным сечением при растяжении и сжатии называется поперечное сечение бруса, в котором возникает максимальное нормальное напряжение. Допускаемые напряжения вычисляются по формуле:
где σпред — предельное напряжение (σпред = σт — для пластических материалов и σпред = σв — для хрупких материалов); [n] — коэффициент запаса прочности. Для пластических материалов [n] = [nт] = 1,2 … 2,5; для хрупких материалов [n] = [nв] = 2 … 5, а для древесины [n] = 8 ÷ 12.
Расчеты на прочность при растяжении и сжатии.
Целью расчета любой конструкции является использование полученных результатов для оценки пригодности этой конструкции к эксплуатации при минимальном расходе материала, что находит отражение в методах расчета на прочность и жесткость.
Условие прочности стержня при его растяжении (сжатии):
При проектном расчете определяется площадь опасного сечения стержня:
При определении допускаемой нагрузки рассчитывается допускаемая нормальная сила:
Расчет на жесткость при растяжении и сжатии.
Работоспособность стержня определяется его предельной деформацией [ l ]. Абсолютное удлинение стержня должно удовлетворять условию:
Часто дополнительно делают расчет на жесткость отдельных участков стержня.
Следующая важная статья теории:
Изгиб балки
Источник
Практическая работа на тему: «Эпюры продольных сил, нормальных напряжений и абсолютных удлинений/укорочений»
Цель работы: изучить тему, научиться строить эпюры продольных сил, нормальных напряжений и абсолютных удлинений/укорочений.
Ход работы:
Изучить теорию.
Построить эпюры.
Оформить работу.
Написать вывод.
Краткая теория:
Продольные силы в поперечных сечениях
Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы N, а прочие силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю.
Это самый простой и часто встречающийся вид деформации. Обычно он наблюдается когда внешняя нагрузка действует вдоль продольной оси стержня. Продольной осью стержня называется линия, проходящая через центры тяжести поперечных сечений.
Обычным является растяжение стержня силами, приложенными к его концам. Передача усилий к стержню может быть осуществлена различными способами, как это показано на рис.1.
Рис. 1
Во всех случаях, однако, система внешних сил образует равнодействующую F, направленную вдоль оси стержня. Поэтому независимо от условий крепления растянутого стержня, расчетная схема в рассматриваемых случаях (рис. 1, а, б) оказывается единой (рис. 1, в) согласно принципу Сен – Венана.
Если воспользоваться методом сечений (рис. 2.), то становится очевидным, что во всех поперечных сечениях стержня возникают нормальные силы Nz, равные силе F (рис. 2, б).
Сжатие отличается от растяжения, формально говоря, только знаком силы Nz. При растяжении нормальная сила Nz направлена от сечения (рис. 2, б), а присжатии – к сечению.
Рис. 2
Растягивающие продольные силы принято считать положительными (рис. 3, а), а сжимающие – отрицательными (рис. 3, б).
Рис. 3
Продольные силы (Nz), возникающие в поперечных сечениях стержня, определяются по внешней нагрузке с помощью метода сечений.
График, показывающий изменение продольных сил по длине оси стержня, называется эпюрой продольных сил (эп. Nz). Он дает наглядное представление о законе изменения продольной силы.
Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня.
Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти Nmax при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным.
Необходимо установить границы участков, в пределах которых закон изменения внутренних сил постоянный. Границами таких участков являются сечения, где приложены сосредоточенные силы или начинается и кончается распределенная нагрузка, а также сечения, где имеется перелом стержня.
Применяя метод сечений и учитывая правила знаков изложенные выше, получаем уравнения изменения внутренних сил в пределах длины каждого участка бруса. Затем, используя, полученные зависимости строим графики (эпюры) этих усилий. Ординаты эпюр в определенном масштабе откладываем от базисной линии, которую проводим параллельно оси бруса.
Таким образом, на основании метода сечений продольная сила в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций внешних сил, приложенных к стержню по одну сторону от рассматриваемого сечения, на его продольную ось.
Причем проекция внешней силы берется со знаком плюс, если сила растягивает часть стержня от точки ее приложения до рассматриваемого сечения и, наоборот, со знаком минус – если сжимает.
Пример 1.
Пусть имеется стержень постоянного поперечного сечения, нагруженный силами 2Р и 3Р вдоль продольной оси стержня, показанный на рис.5. Определить величину внутренних сил.
Рис.5.
Решение.
Стержень может быть разделен на два участка, граничными точками которых являются точки приложения сосредоточенных сил и точка закрепления. Если начало координат расположить на правом конце стержня, а ось z направить справа налево, то, используя метод сечений, рассекая последовательно участки, отбрасывая левую часть, заменяя ее действие внутренними усилиями N, Qy, Mx и уравновешивая оставшуюся часть, получим:
I участок:
Как видно, при растяжении в поперечных сечениях стержня возникает только один внутренний силовой фактор — нормальная сила N.
II участок:
Таким образом, нормальная сила равна алгебраической сумме проекций сил, приложенных к отсеченной части на продольную ось
Полученные результаты для большей наглядности удобно представить в виде графика, (эпюры N), показывающего изменение продольной силы вдоль оси стержня (рис.2.4.1). Построим на первом участке линию параллельную оси z на высоте 2Р, на втором участке – линию со значением —Р. Области ограниченные графиком и осью z принято штриховать и обозначать знак этой области. Видно, что наибольшая продольная сила возникает на первом участке стержня и, как следствие, при прочих равных условиях, он скорее может разрушиться, чем второй участок.
Напряжение в поперечных сечениях стержня
Нормальная сила N приложена в центре тяжести сечения, является равнодействующей внутренних сил в сечении и, в соответствии с этим, определяется следующим образом:
Но из этой формулы нельзя найти закон распределения нормальных напряжений в поперечных сечениях стержня. Для этого обратимся к анализу характера его деформирования.
Если на боковую поверхность этого стержня нанести прямоугольную сетку (рис. 2.2, б), то после нагружения поперечные линии а-а, b-b и т.д. переместятся параллельно самим себе, откуда следует, что все поверхностные продольные волокна удлинятся одинаково. Если предположить также, что и внутренние волокна работают таким же образом, то можно сделать вывод о том, что поперечные сечения в центрально растянутом стержне смещаются параллельно начальным положениям, что соответствует гипотезе плоских сечений (гипотезе Бернулли).
Значит, все продольные волокна стержня находятся в одинаковых условиях, а следовательно, нормальные напряжения во всех точках поперечного сечения должны быть также одинаковы и равны
где A — площадь поперечного сечения стержня.
В сечениях, близких к месту приложения внешних сил, гипотеза Бернулли нарушается: сечения искривляются, и напряжения в них распределяются неравномерно. По мере удаления от сечений, в которых приложены силы, напряжения выравниваются, и в сечениях, удаленных от места приложения сил на расстояние, равное наибольшему из размеров поперечного сечения, напряжения можно считать распределенными по сечению равномерно. Это положение, называемое принципом Сен-Венана, позволяет при определении напряжений в сечениях, достаточно удаленных от мест приложения внешних сил, не учитывать способ их приложения, заменять систему внешних сил статически эквивалентной системой. Например, экспериментально установлено, что во всех трех случаях нагружения стержня (рис. 5, а) значения напряжений в сечениях, удаленных от крайних сечений на расстояние не менее высоты сечения h, одинаковы: (рис. 5, б), а в сечениях, близких к местам приложения внешних сил, распределения напряжений по сечению существенно различны (рис. 5, в).

Рис.5
Высказанное предположение о равномерном распределении нормальных напряжений в поперечном сечении справедливо для участков, достаточно удаленных от мест: резкого изменения площади поперечного сечения (рис. 5, в); скачкообразного изменения внешних нагрузок; скачкообразного изменения физико-механических характеристик конструкций.
Нормальные напряжения при сжатии определяют также, как и при растяжении, но считают отрицательными.
Деформации и перемещения. Закон Гука
Рассмотрим однородный стержень с одним концом, жестко заделанным, и другим — свободным, к которому приложена центральная продольная сила Р (рис. 6). До нагружения стержня его длина равнялась l — после нагружения она стала равной (рис. 6). Величину называют абсолютной продольной деформацией (абсолютным удлинением) стержня. В большинстве случаев оно мало по сравнению с его первоначальной длиной l (∆l<<l).
Рис. 6
Если в нагруженном стержне напряженное состояние является однородным, т.е. все участки стержня находятся в одинаковых условиях, деформация остается одной и той же по длине стержня и равной
Величина ε называется относительной продольной деформацией.
Если же по длине стержня возникает неоднородное напряженное состояние, то для определения его абсолютного удлинения необходимо рассмотреть бесконечно малый элемент длиной dz (рис. 2.8). При растяжении он увеличит свою длину на величину и его деформация составит:
В пределах малых деформаций при простом растяжении или сжатии закон Гука записывается в следующем виде (нормальные напряжения в поперечном сечении прямо пропорциональны относительной линейной деформации ):
Величина Е представляет собой коэффициент пропорциональности, называемый модулем упругости материала первого рода (модуль продольной упругости). Его величина постоянна для каждого материала. Он характеризует жесткость материала, т.е. способность сопротивляться деформированию под действием внешней нагрузки.
Из совместного рассмотрения уравнений (2.5) и (2.6) получим:
откуда с учетом того, что
окончательно получим:
Если стержень изготовлен из однородного изотропного материала с Е = const, имеет постоянное поперечное сечение A = const и нагружен по концам силой Р, то из (2.7) получим
Зависимость (2.8) также выражает закон Гука. Знаменатель EA называется жесткостью при растяжении — сжатии или продольной жесткостью.
Задача №1.
Построить эпюры продольных сил, нормальных напряжений и абсолютного удлинения/укорочения. Данные для своего варианта взять из таблицы. Е=115∙109Па.

Номер варианта
Номер схемы
F1, кН
F2, кН
F3, кН
A1, см2
A2, см2
1
1
10
16
12
5
8
2
2
6
14
8
1,2
3,5
3
3
5
10
14
4
9
4
4
12
14
8
12
7
5
5
14
17
9
10
5
6
6
25
12,5
15
13
15
7
7
36
8
22
5
7
8
8
15
6
26
2
8
9
9
2
8
5
4
6
10
10
7
17
9
8
10
11
1
9
13
17
9
4
12
2
7,5
10
6,8
10
5
13
3
6,8
11
12
13
7
14
4
2,4
5
7
15
18
15
5
3
9
4
17
12
16
6
12
3
5
1,9
2,8
17
7
13
17
22
4,5
5,5
18
8
18
21
30
15
11
19
9
19
14
23
7
10
20
10
20
26
32
12,5
8,5
21
1
6
32
15
10
6
22
2
7
40
20
8
12
23
3
22
10
17
16
9
24
4
28
5
16
3
8
25
5
32
8
24
15
10
26
6
14
9
5
4
7
27
7
23
18
12
12
10
28
8
24
3,5
18
10
5
29
9
10
4,2
9
8
4
30
10
2
12
8
3
5,8
Задача №2 Е=2∙106 МПа
Номер
варианта
Номер схемы
А, см2
F1, кН
F2, кН
L1, м
L2, м
L3, м
1
1
10
10
18
1
1,2
2,2
2
2
12
15
10
0,8
0,5
1,3
3
3
14
20
36
1,4
2
1
4
4
18
36
42
0,4
0,6
0,8
5
5
12
25
36
1,4
0,5
0,1
6
6
5
9
12
0,8
0,6
0,3
7
7
4
2
8
1,2
1,5
0,8
8
8
2,5
8
5
3
2,5
1,5
9
9
3
5
2
0,8
0,2
1,2
10
10
7
5
12
1
1
1,5
11
1
4
6
10
0,2
0,7
1
12
2
10
40
27
1,8
2,4
3
13
3
1,5
8
16
0,5
0,5
0,5
14
4
4,6
4
6
0,2
0,4
0,4
15
5
2
10
14
1,2
1,9
2
16
6
7
6
13
1,2
0,8
1
17
7
9
12
7
1,5
1,2
1,3
18
8
10
25
17
2,2
1,8
2
19
9
2,8
9
15
1
1
1
20
10
3,2
10
16
0,4
0,7
1,3
21
1
4
14
10
0,6
1
0,8
22
2
5,5
13
5
1,2
0,6
1
23
3
2
8
4
1
0,5
0,5
24
4
12
29
19
2,2
2,1
2
25
5
8,5
23
28
1,4
0,8
1
26
6
5
8
14
0,3
0,2
0,1
27
7
6
12
8
0,5
0,8
1
28
8
3,7
10
4
0,1
0,5
0,7
29
9
12
36
25
1
1,2
0,6
30
10
2,8
12
7
0,4
0,6
1,4

Задача №3
Е=3,1∙109Па
Номер варианта
Номер схемы
А1, см2
А2, см2
F1, кН
F2, кН
1
31
1
4
10
12
2
32
2
8
15
19
3
33
3
5
23
28
4
34
5
2
22
18
5
35
7
10
12
8
6
36
8
6
4
9
7
37
9
11
6
9
8
38
11
7
12
17
9
39
2,5
5
3
6
10
40
3.8
7
5
8
11
31
1.2
2.5
12
8
12
32
4
2.2
10
8,5
13
33
5
8
8
4
14
34
12
8
7
5
15
35
2.2
5.5
6
3,6
16
36
3.4
2.2
5
11
17
37
5
3
4
10
18
38
8
2
3
1,5
19
39
10
12
8,5
5
20
40
12
6
14
8
21
31
2.4
6.5
6,6
14,5
22
32
4
2
8
4
23
33
1.5
3.2
8
3,6
24
34
1.8
2.8
10
4,5
25
35
3
4
6
5
26
36
6
9
7
12
27
37
2.2
1.2
3,8
16
28
38
12
9
9
17
29
39
2.4
2.8
12
8
30
40
4
2.2
13
10

Источник
