Построение эпюр всф при растяжении сжатии
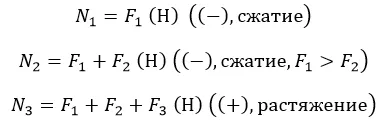
Построение эпюр продольных сил – это решение статически определимой задачи. Производится для выявления картины нагрузки упругого тела. Вернее, уточнения ее схематизации.
Необходимо для определения наиболее напряженного, так называемого «опасного» сечения. Затем методами сопромата (сопротивления материалов) проводится анализ с прогнозированием перемещений элементов конструкции.
Но всему свое время. Сначала немного о терминах.
Основные понятия
Брусом (балкой) называют тело, вытянутое вдоль оси. То есть длина преобладает над шириной и высотой.

Если имеются только осевые (продольные) силы, то объект подвергается растяжению/сжатию. В этом случае в материале возникают только нормальные поперечному сечению силы противодействия и тело считают стержнем.
Статическая определимость подразумевает достаточность схемы для установления внутренних усилий противодействия. Участок – часть балки с неизменным сечением и характерной нагрузкой.
Правила построения учитывают знаки усилий. Растягивающие принимают положительными, сжимающие – отрицательными.
В системе СИ силы измеряются в ньютонах (Н). Длины в метрах (м).
Что такое эпюра продольных сил
Показывает, какой силой (в нашем предположении нормальной) загружен каждый участок. По всей длине стержня. Иначе говоря, эпюра – наглядное графическое изображение изменения нагрузки по всей длине конструкции.
Как построить эпюру продольных сил
Используется метод сечений. Балка виртуально рассекается на каждом участке и ищется противодействующая N. Ведь задача статическая.
Сопротивление рассчитывается по формуле:
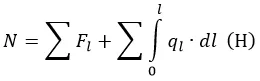
где:
Fl – действующие на участке l силы (Н);
ql – распределенные нагрузки (Н/м).
Порядок построения:
1. Рисуется схема балки и механизмов закрепления;
2. Производится разделение на участки;
3. Для каждого рассчитывается N с учетом знаков. Если у балки есть незакрепленный конец, то начинать удобнее именно с него. В противном случае считается реакция опор. И оптимальнее выбирать сечение с меньшим количеством действующих факторов:
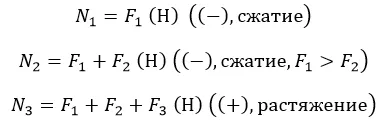
Нетрудно заметить, что последнее уравнение дает еще и реакцию опоры;
4. Параллельно оси стержня намечается база эпюры. Положительные значения масштабировано проставляются выше, отрицательные – ниже. Эпюру наглядно совмещать с расчетной схемой. Итоговый результат и промежуточные сечения показаны на рис. 1.
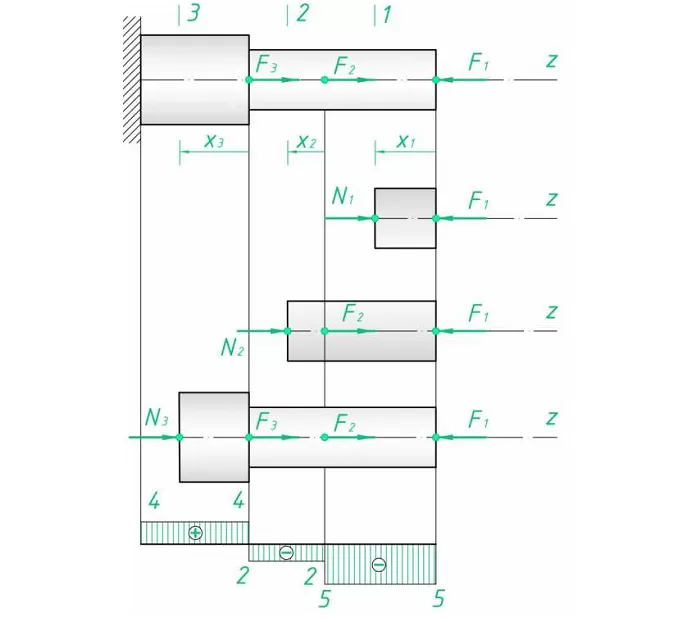
Рис. 1. Эпюра продольных сил
Рассмотрим случай:
F1 = 5 (кН);
F2 = 3 (кН);
F3 = 6 (кН).
Вычислим:
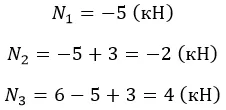
Проверить эпюру можно по скачкам: изменения происходят в точках приложения сил на их величину.
Пример построения эпюр и решения задач
Построить эпюру сил для следующего случая (рис. 2):
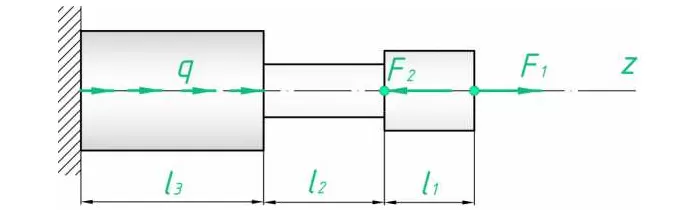
Рис. 2
Дано:
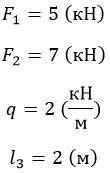
Решение.
Разбиение на участке вполне очевидно. Найдем сопротивление на выделенных:
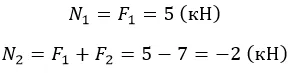
Распределенная нагрузка зависит от длины, на которой приложена. Поскольку нарастает линейно, значение N2 будет постепенно увеличиваться/уменьшаться в зависимости от знака q.
Эпюра такого вида усилия представляет собой прямоугольный треугольник с катетами l3 и ql3 (в масштабе). Поскольку распределение линейно.
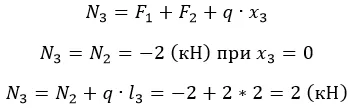
По полученным данным строим эпюру (рис. 3).
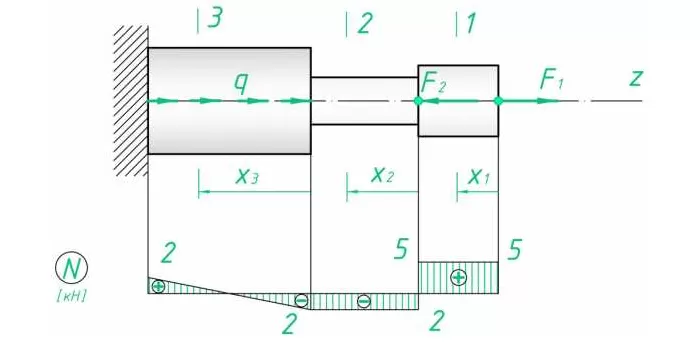
Рис. 3
Заключение
Приведенный алгоритм является предварительным этапом в расчете модели на прочность. «Слабое» место находится уже с учетом площади поперечного сечения.
В сети имеются онлайн сервисы для помощи в расчетах при вычерчивании. Но стоит ли ими пользоваться, если процедура настолько проста? Если не запутаться в знаках, конечно. Это самая распространенная ошибка.
Источник
В различных сечениях одного и того же бруса внутренние силовые факторы различны. Для расчета конструкций на прочность весьма важно знать как величину внутренних силовых факторов, так и характер их изменения по длине бруса, что устанавливается по эпюрам ВСФ.
Эпюрой называется график, характеризующий закон изменения какого-либо параметра (например, ВСФ, напряжения, перемещения, температуры и др.) по длине или высоте составной части конструкции. Эпюра позволяет установить местоположение опасного сечения, где вероятнее всего произойдет разрушение конструкции.
При построении эпюр необходимо придерживаться следующих общих правил и порядка.
Правила построения эпюр ВСФ:
— ось, или база, эпюры выбирается рядом с исходной расчетной схемой;
— ординаты эпюры откладываются от оси в некотором масштабе с учетом знака;
— поле эпюры подвергается штриховке (штриховые линии должны быть перпендикулярны к оси эпюры), внутри него указывается знак и обозначаются характерные ординаты эпюры;
— выше или рядом с эпюрой дается ее название и указывается размерность, если эпюра построена в числовом виде.
Порядок построения эпюр ВСФ:
— расчетная схема заданного бруса разбивается на силовые участки, то есть участки, в пределах которых закон изменения заданного фактора является одним и тем же, т.е. неизменным. Границами силовых участков являются сечения, в пределах которых действуют внешние нагрузки (M, F, q) или изменяются направление оси и поперечные размеры бруса;
— для каждого силового участка применяется метод сечений (правило “РОЗУ”) и составляется общее уравнение искомого ВСФ в виде функции переменной абсциссы z ;
Рисунок 2.6- Пример построения эпюр ВСФ
— по полученным уравнениям определяются характерные ординаты эпюры и выполняется их построение в соответствии с вышерассмотренными правилами (рисунок
При построении эпюр ВСФ предварительно устанавливаются правила знаков, которые являются условными для каждого ВСФ
22) Состояние растяжение-сжатие. Определение напряжений в поперечном сечении (без учета и с учетом собственного веса).
Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы , а прочие силовые факторы равны нулю.
Рассмотрим однородный прямолинейный стержень длиной и площадью поперечного сечения А, на двух концах которого приложены две равные по величине и противоположно направленные центральные продольные силы Р (рис. 2.2, а).
Продольная сила – внутреннее усилие, равное сумме проекций всех внешних сил, взятых с одной стороны от сечения, на ось стержня. Примем следующее правило знаков для продольной силы: растягивающая продольная сила положительна, сжимающая – отрицательна (рис. 2.1).
Рис.2.1
Поместим начало плоской системы координат yz в центре тяжести левого сечения, а ось направим вдоль продольной оси стержня.
Для определения величин внутренних усилий воспользуемся методом сечений. Задавая некоторое сечение на расстояние z ( ) от начала системы координат и рассматривая равновесие левой относительно заданного сечения части стержня (рис. 2.2, б), приходим к следующему уравнению:
,
откуда следует, что
.
Следовательно, продольная сила в сечении численно равна сумме проекций на ось стержня всех сил, расположенных по одну сторону сечения
(2.1)
Рис. 2.2
Для наглядного представления о характере распределения продольных сил по длине стержня строится эпюра продольных сил . Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня.
Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти Nmax при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным.
Отсутствует пример расчета. Его я не нашел к сожалению.
23) Определение деформации при растяжении-сжатии.
Oпыты показывают, что при растяжении длина стержня увеличивается, а поперечные размеры уменьшаются, при сжатии — наоборот (рис.2.7).
Абсолютная продольная и поперечная деформации равны
; .
Относительная продольная деформация e и относительная поперечная деформация e‘ равны
; .
В пределах малых удлинений для большинства материалов справедлив закон Гука — нормальные напряжения в поперечном сечении прямо пропорциональны относительной линейной деформацииe
. (2.2)
Коэффициент пропорциональности E — модуль продольной упругости, его величина постоянна для каждого материала. Он характеризует жесткость материала, т.е. способность сопротивляться деформированию под действием внешней нагрузки.
Средние значения E и m для некоторых материалов даны в таблице 1.1.
Таблица 1.1
Значения модуля упругости Е и коэффициента Пуассона n
| Материал | Е, МПа | n |
| Сталь | (2-2.2)×105 | 0.24-0.3 |
| Титан | 1.1×105 | 0.25 |
| Алюминий | 0.7×105 | 0.32-0.36 |
| Медь | 1.0×105 | 0.31-0.34 |
| Чугун | (1.1-1.6)×105 | 0.23-0.27 |
| Резина | 1.0-0.8 | 0.5 |
| Пробка | — | |
| Стекловолокно | (0.18-0.4)×105 | 0.25 |
| Дерево | 1×104 | — |
Так как , а , то подставляя в закон Гука (2.2) можно получить формулу для определения абсолютного удлинения (укорочения) стержня
.
Эта зависимость также выражает закон Гука.
Знаменатель EF называется жесткостью при растяжении — сжатии или продольной жесткостью.
Отношение относительной поперечной деформации e’ к относительной продольной деформации e, взятое по модулю, называется коэффициентом поперечной деформации или коэффициентом Пуассона
.
Эта величина является постоянной для каждого материала и определяется экспериментально.
Значения n для различных материалов изменяются в пределах (n = 0 у пробки, n = 0,5 у резины). Для большинства конструкционных материалов n =0,25…0,33 (табл. 1.1).
E и n являются основными характеристиками упругости изотропного материала.
24) Закон Гука при растяжении-сжатии и сдвиге.
Растяжение сжатие:
Закон Гука выражает прямо пропорциональную зависимость между нормальным напряжением и относительной деформацией: или, если представить в другом виде: где Е — модуль продольной упругости. Это физическая постоянная материапа, характеризующая его способность сопротивпяться упругому деформированию.
Закон Гука при сдвиге: g = t/G или t = G×g .
G — модуль сдвига или модуль упругости второго рода [МПа] — постоянная материала, характеризующая способность сопротивляться деформациям при сдвиге. (Е — модуль упругости, m— коэффициент Пуассона).
Потенциальная энергия при сдвиге: .
Удельная потенциальная энергия деформации при сдвиге: ,
где V=а×F — объем элемента. Учитывая закон Гука, .
Вся потенциальная энергия при чистом сдвиге расходуется только на изменение формы, изменение объема при деформации сдвига равно нулю.
Закон Пуассона.
вероятность возникновения случайного события n раз за время t. l — интенсивность случайного события.
Свойства:
1) МО числа событий за время t: М = l*t.
2) среднеквадратическое отклонение числа событий , для данного распределения М = D.
Распределение Пуассона получается из биноминального, если число испытаний m неограниченно возрастает, а МО числа событий остается постоянным.
Закон Пуассона используется в том случае когда необходимо определить вероятность того что за данное время произойдет 1,2,3…отказов.
Источник
1. На рисунке проводиться ось ОХ, совпадающая с продольной осью стержня.
2. Под рисунком стержня проводятся две базовые нулевые линии, параллельно продольной оси стержня. Одна для эпюры продольной силы Nz
Вторая базовая нулевая линия для эпюры нормальных напряжений (Мпа).
3. Стержень разбивается на участки. Для границ участков проводятся вертикальные линии в точках приложения нагрузки и изменения площади поперечного сечения вниз до пересечения с базовыми нулевыми линиями. Нумерация участков начинается со свободной стороны стержня для задачи статически определимой. Если задача статически неопределимая, то нумерация выполняется слева направо.
4. Для определения значения продольной силы используется метод сечений. В середине участка проводится сечение. Указывается направление продольной силы. Положительным считается направление продольной силы, направленной от сечения (растягивает). Значение продольной силы Nz определяется из условия равновесия отсечённой части (сумма проекций на ось ох всех действующих сил равна нулю 0).
5. Вычисляем значение нормальных напряжений.
6. Положительные значения продольной силы и нормального напряжения откладываем вверх от базовой нулевой линии, отрицательные вниз.
7. Проверяем правильность решения задачи по эпюре продольной силы. В точках, где приложена сосредоточенная сила, на эпюре должен быть скачок равный значению продольной силы.
8. Условие прочности проверяем по эпюре нормальных напряжений. Максимальные напряжения, возникающие в конструкции, не должны превышать допускаемых.
Пример №1: Построить эпюры продольной силы N и нормального напряжения σ, проверить на прочность стальной стержень, закрепленный с одной стороны (статически определимая задача). Р1 = 10кН Р2 = 15кН
Р3 =15кН
=100 Мпа; А1 = F; А2 = 2F; F = 100 мм2
Решение:
Параллельно продольной оси стержня проводим две базовые нулевые линии для продольной силы и нормального напряжения.
Разбиваем стержень на участки, начиная со свободной стороны. Проводим вниз вертикальные линии в точках приложения сил и изменения площади поперечного сечения до пересечения с нулевыми линиями. Нумерация участков начинается со свободной стороны стержня.
1 участок:
— на первом участке проводим сечение, перпендикулярное продольной оси, мысленно отбрасываем большую часть и рассматриваем меньшую часть стержня. Заменяем действие отброшенной части на оставленную продольной силой N1. Положительным считается действие от сечения (растягивает).
Рассматриваем равновесие оставленной части, проецируя действующие силы на ось ОХ:
Определяем продольную силу на первом участке:
-N1+ Р1=0 следовательно N1 = Р1=10 кН
Определяем нормальное напряжение на первом участке
2 участок:
-N2+ Р1 — Р2=0 следовательно N2 = Р1-Р2 =10-15= -5 кН
3 участок:
-N3+ Р1 — Р2=0 следовательно N3 = Р1-Р2 =10-15= -5 кН
4 участок:
-N4+ Р1 — Р2+Р3=0 следовательно N4 = Р1-Р2+Р3=10-15+15= 10 кН
Рис. 10.
Метод сечений для определения продольной силы.
Для построения эпюр продольной силы и нормального напряжения задаёмся произвольным масштабом (например: одна клеточка -5 кН и -25 мегапаскалей). Строим эпюры продольной силы и нормального напряжения, откладывая положительные значения вверх от базовой нулевой линии, отрицательные вниз.
Проверяем правильность решения задачи по эпюре продольной силы, в точке приложения сосредоточенной силы на эпюре должен быть скачок, равный действующей силе.
По эпюре нормального напряжения проверяем условие прочности максимальные напряжения должны быть меньше или равны допустимым, значит прочность обеспечена.
Рис.11.
Эпюры продольной силы N и нормального напряжения σ.
СПИСОК ЛИТЕРАТУРЫ
1. Рубашкин А.Г. Лабораторные работы по сопротивлению материалов.- М.: Высшая школа, 1961.-159с.
2. Афанасьев A.M., Марьин В.А. Лабораторный практикум по сопротивлению материалов.- М.: Наука, 1975.-284с.
3. Феодосьев В.И. Сопротивление материалов.- М.: Наука, 1979.-559с.
4. Писаренко Г.С. Сопротивление материалов.- Киев.: Высшая школа, 1973.-667с.
Источник
В общем случае при действии внешних нагрузок в поперечных сечениях элементов конструкции возникают три внутренних силовых фактора: поперечная сила Q, продольная сила N и изгибающий момент M.
Продольная сила N в произвольном поперечном сечении балки численно равна алгебраической сумме проекций на ось балки всех сил, действующих по одну сторону от рассматриваемого сечения.
Поперечная сила Q в произвольном поперечном сечении балки численно равна алгебраической сумме проекций на нормаль к оси балки всех сил, действующих по одну сторону от рассматриваемого сечения.
Изгибающий момент М в произвольном поперечном сечении балки численно равен алгебраической сумме моментов всех сил, действующих по одну сторону от рассматриваемого сечения.
Для определения внутренних силовых факторов используется метод сечений. При построении эпюр необходимо руководствоваться правилами знаков поперечных, продольных сил и изгибающих моментов (рисунок 2.1):
– продольная сила N считается положительной, если внешние силы относительно рассматриваемого сечения вызывают растяжение;
– поперечная сила Q считается положительной, если внешние силы относительно рассматриваемого сечения вращают отсеченную часть балки по ходу часовой стрелки;
– изгибающий момент M считается положительным, если внешние нагрузки относительно рассматриваемого сечения растягивают нижние волокна.
Рисунок 2.1 – Правило знаков внутренних силовых факторов
Для определения величины опорных реакций применяют три известных уравнения статики:
, , ,
где А, В – моментные точки, которыми чаще всего выступают опоры.
Причем последнее уравнение служит для проверки правильности определения неизвестных реакций. Следует также отметить, что если в результате расчета реакция получается отрицательной, то ее направление на расчетной схеме изменяют на противоположное, а само значение реакции при этом будет положительным.При составлении уравнений статики для определения опорных реакций рекомендуется придерживаться правил, принятых в теоретической механике, или же следующих правил знаков:
— сила принимается положительной, если ее направление совпадает с выбранным положительным направлением координатной оси;
— моменты сил, вращающие в одну сторону относительно моментной точки, имеют одинаковый знак.
Построение эпюр внутренних силовых факторов в системах с жестким защемлением производится без определения реакций, действующих в заделке, путем рассмотрения характерных участков конструкции со свободного (незащищенного) конца.
Границами характерных участков балки являются опорные сечения, точки приложения сосредоточенных сил или моментов, начало и окончание действия распределенной нагрузки. В рамах к характерным сечениям относятся также узлы. На каждом участке проводится произвольное сечение на расстоянии z от начала соответствующего участка, составляются в общем виде выражения для действующих ВСФ с учетом правила знаков, и в полученные выражения подставляются границы характерного сечения. Полученные значения ВСФ откладываются на соответствующих эпюрах под характерными участками перпендикулярно нулевой линии.
После построения эпюр производится контроль правильности их построения:
а)Если участок балки нагружен сосредоточенной силой, то эпюра поперечных сил на данном участке будет очерчена прямой линией, параллельной нулевой линии эпюры. Изгибающий момент на участке будет изменяться по линейному закону.
б) На участках с распределенной нагрузкой эпюра очерчивается прямой наклонной линией, а эпюра – квадратной параболой с выпуклостью, направленной навстречу действию распределенной нагрузки. Если на участке с эпюра пересекает нулевую линию эпюры, то под этой точкой пересечения изгибающий момент будет иметь экстремальной значение.
в) В сечении, где приложена внешняя сосредоточенная сила, на эпюре Q будет скачок на величину и в направлении действия этой внешней силы.
г) В сечении, где приложен внешний сосредоточенный момент, на эпюре М будет наблюдаться скачок на величину и в направлении действия этого внешнего момента.
В отличие от балок, ось рамы представляет собой ломаную линию. Нулевые линии эпюр также представляют в виде ломаных линий, а каждый характерный участок можно рассматривать как отдельную балку. При определении величин продольных и поперечных сил применяется правило знаков, представленное на рисунке 2.1. При построении эпюр Q и N положительные ординаты откладывают с внешней стороны контура рамы, а отрицательные – внутри контура. При составлении выражения изгибающего момента руководствуются произвольным правилом знаков. Например, все нагрузки, которые будут сжимать наружные волокна рамы, принимают со знаком «плюс». В любом случае, эпюра М строится со стороны сжатого волокна, причем знак на ней не указывается. Также следует помнить, что узлы рамы должны находиться в равновесии, то есть сумма изгибающих моментов в примыкающих к узлу сечениях должна равняться нулю или, если в этом узле приложен внешний сосредоточенный изгибающий момент, значению этого момента.
Пример построения эпюр внутренних силовых факторов для балки
Исходные данные: расчетная схема балки с указанием численных величин нагрузок и линейных размеров.
Требуется: построить эпюры внутренних силовых факторов.
В поперечных сечениях балки возникают два ВСФ: поперечная сила (Q) и изгибающий момент (M). Вычерчиваем заданную балку с указанием всех нагрузок и линейных размеров. Определяем реакции опор.
;
;
;
;
Проверка правильности определения реакций:
.
Разбиваем балку на участки, на каждом из которых проводим произвольное поперечное сечение на расстоянии z от начала соответствующего участка (см. рисунок 2.2, а). Изображаем нулевые линии для построения эпюр поперечных сил (эпюра Q) и эпюры изгибающего момента (эпюра М). Записываем в общем виде выражения для определения ВСФ для каждого участка балки и при помощи полученных уравнений рассчитываем их численные значения в характерных сечениях.
Рисунок 2.2 – Расчетная схема балки и эпюры внутренних силовых факторов
1 участок: .
;
.
2 участок: .
;
Так как на этом участке эпюра Q пересекает нейтральную линию, то в этой точке пересечения изгибающий момент будет иметь экстремальное значение:
;
откуда ;
.
3 участок: .
;
Полученные точки соединяем линиями, замыкающими поле эпюры. В поле эпюры в кружке ставим знак рассматриваемого внутреннего силового фактора и наносим штриховку. Линии штриховки перпендикулярны нулевой линии эпюры (рисунок 2.2, б, в).
Пример построения эпюр внутренних силовых факторов в раме
Исходные данные: расчетная схема рамы с указанием численных величин нагрузок и линейных размеров.
Требуется: построить эпюры внутренних силовых факторов.
Вычерчиваем заданную раму (рисунок 2.3, а) с указанием всех нагрузок и линейных размеров в численном виде. Определяем реакции опор:
;
;
;
;
;
.
Проверка правильности определения реакций:
.
Разбиваем раму на участки, на каждом из которых проводим произвольное поперечное сечение на расстоянии z от начала соответствующего участка (см. рисунок 2.3, а). Изображаем нулевые линии для построения эпюр нормальных (эпюра N) и поперечных (эпюра Q) сил, эпюры изгибающего момента (эпюра М).
Рисунок 2.3 – Расчетная схема рамы и эпюры внутренних силовых факторов
Записываем в общем виде выражения для определения ВСФ для каждого участка рамы и при помощи полученных уравнений рассчитываем их численные значения в характерных сечениях рамы.
1 участок: .
;
;
.
2 участок: .
;
;
.
3 участок: .
;
;
.
4 участок: .
;
;
Так как на четвертом участке эпюра Q пересекает нулевую линию, требуется провести исследование на экстремум:
;
откуда ;
.
Строим эпюры поперечных и продольных сил, изгибающих моментов (рисунок 2.3, б−г). Проверяем равновесие узлов рамы (рисунок 2.3, д) – узлы уравновешены.
3 Расчетно-проектировочное задание №3. Расчет статически определимой балки при изгибе
Источник
