Построение эпюр перемещений при растяжении и сжатии

1. На рисунке проводиться ось ОХ, совпадающая с продольной осью стержня.
2. Под рисунком стержня проводятся две базовые нулевые линии, параллельно продольной оси стержня. Одна для эпюры продольной силы Nz
Вторая базовая нулевая линия для эпюры нормальных напряжений (Мпа).
3. Стержень разбивается на участки. Для границ участков проводятся вертикальные линии в точках приложения нагрузки и изменения площади поперечного сечения вниз до пересечения с базовыми нулевыми линиями. Нумерация участков начинается со свободной стороны стержня для задачи статически определимой. Если задача статически неопределимая, то нумерация выполняется слева направо.
4. Для определения значения продольной силы используется метод сечений. В середине участка проводится сечение. Указывается направление продольной силы. Положительным считается направление продольной силы, направленной от сечения (растягивает). Значение продольной силы Nz определяется из условия равновесия отсечённой части (сумма проекций на ось ох всех действующих сил равна нулю 0).
5. Вычисляем значение нормальных напряжений.
6. Положительные значения продольной силы и нормального напряжения откладываем вверх от базовой нулевой линии, отрицательные вниз.
7. Проверяем правильность решения задачи по эпюре продольной силы. В точках, где приложена сосредоточенная сила, на эпюре должен быть скачок равный значению продольной силы.
8. Условие прочности проверяем по эпюре нормальных напряжений. Максимальные напряжения, возникающие в конструкции, не должны превышать допускаемых.
Пример №1: Построить эпюры продольной силы N и нормального напряжения σ, проверить на прочность стальной стержень, закрепленный с одной стороны (статически определимая задача). Р1 = 10кН Р2 = 15кН
Р3 =15кН
=100 Мпа; А1 = F; А2 = 2F; F = 100 мм2
Решение:
Параллельно продольной оси стержня проводим две базовые нулевые линии для продольной силы и нормального напряжения.
Разбиваем стержень на участки, начиная со свободной стороны. Проводим вниз вертикальные линии в точках приложения сил и изменения площади поперечного сечения до пересечения с нулевыми линиями. Нумерация участков начинается со свободной стороны стержня.
1 участок:
— на первом участке проводим сечение, перпендикулярное продольной оси, мысленно отбрасываем большую часть и рассматриваем меньшую часть стержня. Заменяем действие отброшенной части на оставленную продольной силой N1. Положительным считается действие от сечения (растягивает).
Рассматриваем равновесие оставленной части, проецируя действующие силы на ось ОХ:
Определяем продольную силу на первом участке:
-N1+ Р1=0 следовательно N1 = Р1=10 кН
Определяем нормальное напряжение на первом участке
2 участок:
-N2+ Р1 — Р2=0 следовательно N2 = Р1-Р2 =10-15= -5 кН
3 участок:
-N3+ Р1 — Р2=0 следовательно N3 = Р1-Р2 =10-15= -5 кН
4 участок:
-N4+ Р1 — Р2+Р3=0 следовательно N4 = Р1-Р2+Р3=10-15+15= 10 кН
Рис. 10.
Метод сечений для определения продольной силы.
Для построения эпюр продольной силы и нормального напряжения задаёмся произвольным масштабом (например: одна клеточка -5 кН и -25 мегапаскалей). Строим эпюры продольной силы и нормального напряжения, откладывая положительные значения вверх от базовой нулевой линии, отрицательные вниз.
Проверяем правильность решения задачи по эпюре продольной силы, в точке приложения сосредоточенной силы на эпюре должен быть скачок, равный действующей силе.
По эпюре нормального напряжения проверяем условие прочности максимальные напряжения должны быть меньше или равны допустимым, значит прочность обеспечена.
Рис.11.
Эпюры продольной силы N и нормального напряжения σ.
СПИСОК ЛИТЕРАТУРЫ
1. Рубашкин А.Г. Лабораторные работы по сопротивлению материалов.- М.: Высшая школа, 1961.-159с.
2. Афанасьев A.M., Марьин В.А. Лабораторный практикум по сопротивлению материалов.- М.: Наука, 1975.-284с.
3. Феодосьев В.И. Сопротивление материалов.- М.: Наука, 1979.-559с.
4. Писаренко Г.С. Сопротивление материалов.- Киев.: Высшая школа, 1973.-667с.
Источник
Определение перемещений
Задание
Для заданного статически определимого стального бруса требуется:
1) построить эпюры продольных сил N и нормальных напряжений σ, записав в общем виде для каждого участка выражения N и σ и указав на эпюрах их значения в характерных сечениях;
2) определить общее перемещение бруса и построить эпюру перемещений δ поперечных сечений, приняв модуль упругости Е = 2·10 МПа.
Цель работы– научиться строить эпюры продольных сил и нормальных напряжений, и определять перемещения.
Теоретическое обоснование
Виды нагружения бруса, при котором в его поперечном сечении возникает только один внутренний силовой фактор – , называемый растяжением или сжатием. Равнодействующая внешних сил прикладывается в центре тяжести поперечного сечения и действует вдоль продольной оси. Внутренние силы определяются с помощью метода сечений. Нормальная сила в сечении бруса является равнодействующей нормальных напряжений, действующих в плоскости поперечного сечения
N = ∑F (5.1).
Величина продольных сил в разных сечениях бруса неодинакова. График, показывающий изменение величины продольных сил в сечении бруса по его длине, называется эпюрой продольных сил.
Закон распределения напряжений может быть определен из эксперимента. Установлено, что если на стержень нанести прямоугольную сетку, то после приложения продольной нагрузки вид сетки не изменится, она по-прежнему останется прямоугольной, а все линии прямыми. Поэтому можно сделать вывод о равномерном по сечению распределении продольных деформаций, а на основании закона Гука (σ = Eε) и нормальных напряжений S = const. Тогда N = S· F , откуда получим формулу для определения нормальных напряжений в поперечном сечении при растяжении
σ = МПа (5.2)
A – площадь около рассматриваемого участка бруса;
N– равнодействующая внутренних сил в пределах этой площадки (согласно метода сечений).
Для обеспечения прочности стержня должно выполняться условие прочности — конструкция будет прочной, если максимальное напряжение ни в одной точке нагруженной конструкции не превышает допускаемой величины, определяемой свойствами данного материала и условиями работы конструкции, то есть
σ ≤ [σ ], τ ≤ [τ] (5.3)
При деформации бруса меняется его длина на и поперечный размер – на . Эти величины зависят и от начальных размеров бруса.
Поэтому рассматривают
– продольная деформация; (5.4)
– поперечная деформация. (5.5)
Экспериментально показано, что , где μ = 0, …, 0,5 – коэффициент Пуассона. Примеры: μ=0 – пробка, μ=0,5 – резина, – сталь.
В пределах упругой деформации выполняется закон Гука: , где E – модуль упругости, или модуль Юнга.
Порядок выполнения работы
1. Разбиваем брус на участки, ограниченные точками приложения сил (нумерацию участков ведем от незакрепленного конца);
2. Используя метод сечений, определяем величину продольных сил в сечении каждого участка: N = ∑F ;
3. Выбираем масштаб и строим эпюру продольных сил, т.е. под изображением бруса (или рядом) проводим прямую, параллельную его оси, и от этой прямой проводим перпендикулярные отрезки, соответствующие в выбранном масштабе продольным силам (положительное значение откладываем вверх (или вправо), отрицательное – вниз (или влево).
4. Определяем общее перемещение бруса и строим эпюру перемещений δ поперечных сечений.
5. Ответить на контрольные вопросы.
Контрольные вопросы
1. Что называется стержнем?
2. Какой вид нагружения стержня называются осевым растяжением (сжатием)?
3. Как вычисляется значение продольной силы в произвольном поперечном сечении стержня?
4. Что такое эпюра продольных сил и как она строится?
5. Как распределены нормальные напряжения в поперечных сечениях центрально-растянутого или центрально-сжатого стержня, и по какой формуле они определяются?
6. Что называется удлинением стержня (абсолютной продольной деформацией)? Что такое относительная продольная деформация? Каковы размерности абсолютной и относительной продольных деформаций?
7. Что называется модулем упругости Е? Как влияет величина Е на деформации стержня?
8. Сформулируйте закон Гука. Напишите формулы для абсолютной и относительной продольных деформаций стержня.
9. Что происходит с поперечными размерами стержня при его растяжении (сжатии)?
10. Что такое коэффициент Пуассона? В каких пределах он изменяется?
11. С какой целью проводятся механические испытания материалов? Какие напряжения являются опасными для пластичных и хрупких материалов?
Пример выполнения
Построить эпюры продольных сил и нормальных напряжений для нагруженного стального бруса (рис. 5.1). Определить удлинение (укорочение) бруса, если E
Рис.5.1
Дано: F = 2 kH, F = 5 kH, F = 2 kH, A = 2 см , А , l = 100 мм, l = 50 мм, l = 200 мм,
l = 150 мм.
Решение. Определяем продольные силы и строим их эпюру:
N = — F = — 2kH;
N = — F + F = -2 + 5 = 3 kH;
N = — F + F = 3 kH;
N = — F + F + F = -2 +5 + 2 = 5 kH
Определяем величину нормальных напряжений и строим их эпюру:
Используя видоизмененный закон Гука, определяем удлинение бруса:
Практическая работа № 6
Источник
ОЦЕНОЧНЫЕ СРЕДСТВА ПО ДИСЦИПЛИНЕ

УТВЕРЖДАЮ Декан факультета сервиса к.т.н., доцент Сумзина Л.В ОЦЕНОЧНЫЕ СРЕДСТВА ПО ДИСЦИПЛИНЕ Материаловедение основной образовательной программы высшего образования программы специалитета по направлению
Подробнее
МЕТОДИЧЕСКИЕ УКАЗАНИЯ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Государственное образовательное учреждение высшего профессионального образования «ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ» МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Подробнее
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «Ивановская государственная текстильная академия» (ИГТА) Кафедра теоретической механики
Подробнее
Экзаменационный билет 3

Экзаменационный билет 1 1. Реальный объект и расчетная схема. Силы внешние и внутренние. Метод сечений. Основные виды нагружения бруса. 2. Понятие об усталостной прочности. Экзаменационный билет 2 1. Растяжение
Подробнее
ОЦЕНОЧНЫЕ СРЕДСТВА ПО ДИСЦИПЛИНЕ

ОЦЕНОЧНЫЕ СРЕДСТВА ПО ДИСЦИПЛИНЕ ОПД.Ф.12.5 ОСНОВЫ ФУНКЦИОНИРОВАНИЯ СИСТЕМ СЕРВИСА. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА основной образовательной программы высшего образования программы специалитета Специальность: 100101.65
Подробнее
Расчеты стержней на прочность и жесткость

Расчеты стержней на прочность и жесткость 1. Стержень с квадратным поперечным сечением а=20см (см. рисунок) нагружен силой. Модуль упругости материала E=200ГПа.. Допускаемое напряжение. Допустимое перемещение
Подробнее
Простые виды сопротивления прямых брусьев

Приложение Министерство сельского хозяйства Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования Саратовский государственный аграрный университет имени
Подробнее
Указания к выполнению контрольной работы 3

Указания к выполнению контрольной работы Пример решения задачи 7 Для стального стержня (рис..) круглого поперечного сечения, находящегося под действием осевых сил F и F и F, требуется: ) построить в масштабе
Подробнее
По предпоследней цифре матрикула

Растяжение-сжатие Работа a Определить при каком значении растягивающей силы F стальной стержень ступенчатого сечения (рис.а) удлинится на мм. Определить при найденной величине F нормальные напряжения в
Подробнее
Числовые данные к задаче 2

ЗАДАЧА Абсолютно жесткий брус АВ опирается на шарнирно-неподвижную опору и прикреплен с помощью шарниров к двум стальным стержням. ребуется подобрать сечения стержней по условию их прочности, приняв запас
Подробнее
(шифр и наименование направления)

Дисциплина Направление Сопротивление материалов 270800 — Строительство (шифр и наименование направления) Специальность 270800 62 00 01 Промышленное и гражданское строительство 270800 62 00 03 Городское
Подробнее
290300, , , , ,

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ УХТИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Анализ внутренних силовых факторов МЕТОДИЧЕСКИЕ УКАЗАНИЯ УХТА 2002 УДК 539.3/6 А-72 Андронов И. Н. Анализ
Подробнее
Расчет плоской рамы методом перемещений

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Государственное образовательное учреждение высшего профессионального образования УЛЬЯНОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Расчет плоской
Подробнее
МЕТОДИЧЕСКИЕ УКАЗАНИЯ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ТЮМЕНСКАЯ ГОСУДАРСТВЕННАЯ АРХИТЕКТУРНО-СТРОИТЕЛЬНАЯ АКАДЕМИЯ КАФЕДРА «СТРОИТЕЛЬНАЯ МЕХАНИКА» СЕКЦИЯ «СОПРОТИВЛЕНИЕ
Подробнее
Основные понятия, определения

Основные понятия, определения 1. Тело, один размер которого намного превышает два других, называется 2. Сопротивление материалов это наука о элементов конструкций Ответ: 1) прочности, жесткости и однородности;
Подробнее
РАСЧЕТ ЭЛЕМЕНТОВ СТАЛЬНЫХ КОНСТРУКЦИЙ

Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Томский государственный архитектурно-строительный университет»
Подробнее
ТЕХНИЧЕСКАЯ МЕХАНИКА

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ АСТРАХАНСКОЙ ОБЛАСТИ Государственное автономное образовательное учреждение Астраханской области высшего профессионального образования «АСТРАХАНСКИЙ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ
Подробнее
1. ЦЕЛИ ОСВОЕНИЯ ДИСЦИПЛИНЫ

1. ЦЕЛИ ОСВОЕНИЯ ДИСЦИПЛИНЫ Дисциплина «Техническая механика» является частью модуля «Механика», представляет собой начальную ступень изучения дисциплины «Сопротивление материалов». Эта особенность обусловливает
Подробнее
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ

Глава 8 СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ 8.1. Шарнирно закрепленное твердое тело на упругих стержнях Постановка задачи. Определить усилия в стержнях статически неопределимой системы, состоящей из шарнирно
Подробнее
ОГЛАВЛЕНИЕ. Предисловие… 4 Введение… 7

ОГЛАВЛЕНИЕ Предисловие… 4 Введение… 7 Глава 1. Механика абсолютно твердого тела. Статика… 8 1.1. Общие положения… 8 1.1.1. Модель абсолютно твердого тела… 9 1.1.2. Сила и проекция силы на ось.
Подробнее
УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ
Подробнее
РАСЧЁТ СТЕРЖНЯ НА ВНЕЦЕНТРЕННОЕ СЖАТИЕ

Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Комсомольский-на-Амуре государственный технический
Подробнее
Задачи к экзамену Задача 1. Задача 2.

Вопросы к экзамену 1. Модель упругого тела, основные гипотезы и допущения. Механика твердого тела, основные разделы. 2. Внешние и внутренние силы, напряжения и деформации. Принцип независимого действия
Подробнее
ПРИКЛАДНАЯ МЕХАНИКА ПОСОБИЕ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ВОЗДУШНОГО ТРАНСПОРТА ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ГРАЖДАНСКОЙ
Подробнее
Решение: Исходные данные: = 2 = 2 = 2

Задача 1 Для данного бруса требуется: — вычертить расчетную схему в определенном масштабе, указать все размеры и величины нагрузок; — построить эпюру продольных сил; — построить эпюру напряжений; — для
Подробнее
1. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ

1. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ 1.1. Статически неопределимые стержневые системы Статически неопределимыми системами называются системы, для которых, пользуясь только условиями статики, нельзя определить
Подробнее
Источник
Задание
Для заданного
статически определимого стального
бруса требуется:
построить эпюры
продольных сил N
и нормальных напряжений σ, записав в
общем виде для каждого участка выражения
Nи σ и указав
на эпюрах их значения в характерных
сечениях;определить общее
перемещение бруса и построить эпюру
перемещений δ
поперечных сечений, приняв модуль
упругости Е = 2·10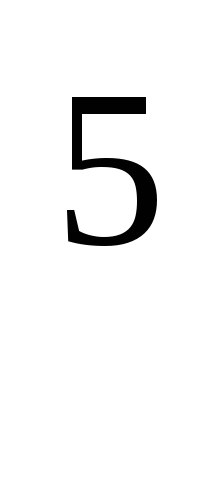 МПа.
МПа.
Цель работы
–
научиться строить эпюры продольных сил
и нормальных напряжений, и
определять перемещения.
Теоретическое
обоснование
Виды
нагружения бруса, при котором в его
поперечном сечении возникает только
один внутренний силовой фактор – ![]() ,
,
называемый растяжением
или сжатием.
Равнодействующая внешних сил прикладывается
в центре тяжести поперечного сечения
и действует вдоль продольной оси.
Внутренние силы определяются с помощью
метода сечений. Нормальная сила в сечении
бруса является равнодействующей
нормальных напряжений, действующих в
плоскости поперечного сечения
N
= ∑F![]()
(5.1).
Величина продольных
сил в разных сечениях бруса неодинакова.
График, показывающий изменение величины
продольных сил в сечении бруса по его
длине, называется эпюрой
продольных сил.
Закон распределения
напряжений может быть определен из
эксперимента. Установлено, что если на
стержень нанести прямоугольную сетку,
то после приложения продольной нагрузки
вид сетки не изменится, она по-прежнему
останется прямоугольной, а все линии
прямыми. Поэтому можно сделать вывод о
равномерном по сечению распределении
продольных деформаций, а на основании
закона Гука (σ
= Eε)
и нормальных напряжений S
= const. Тогда N = S·
F , откуда получим формулу для определения
нормальных напряжений в поперечном
сечении при растяжении
σ![]() =
=
![]() МПа
МПа
(5.2)
A
– площадь около рассматриваемого
участка бруса;
N–
равнодействующая внутренних сил в
пределах этой площадки (согласно метода
сечений).
Для обеспечения
прочности стержня должно выполняться
условие прочности — конструкция будет
прочной, если максимальное напряжение
ни в одной точке нагруженной конструкции
не превышает допускаемой величины,
определяемой свойствами данного
материала и условиями работы конструкции,
то есть
σ
≤ [σ ], τ ≤ [τ]
(5.3)
При
деформации бруса меняется его длина на
![]()
и поперечный размер – на ![]() .
.
Эти величины зависят и от начальных
размеров бруса.
Поэтому рассматривают
![]() –
–
продольная
деформация;
(5.4)
![]() –
–
поперечная
деформация. (5.5)
Экспериментально
показано, что ![]() ,
,
где μ = 0, …, 0,5 – коэффициент Пуассона.
Примеры: μ=0 – пробка, μ=0,5 – резина, ![]()
– сталь.
В
пределах упругой деформации выполняется
закон Гука: ![]() ,
,
где E
– модуль упругости, или модуль Юнга.
Порядок
выполнения работы
Разбиваем брус
на участки, ограниченные точками
приложения сил (нумерацию участков
ведем от незакрепленного конца);Используя метод
сечений, определяем величину продольных
сил в сечении каждого участка:
N
= ∑F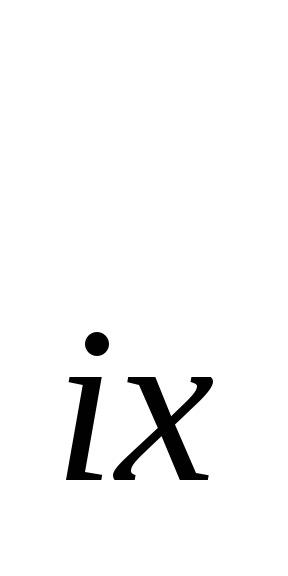
;Выбираем масштаб
и строим эпюру продольных сил, т.е. под
изображением бруса (или рядом) проводим
прямую, параллельную его оси, и от этой
прямой проводим перпендикулярные
отрезки, соответствующие в выбранном
масштабе продольным силам (положительное
значение откладываем вверх (или вправо),
отрицательное – вниз (или влево).Определяем
общее перемещение бруса и строим эпюру
перемещений δ
поперечных сечений.Ответить на
контрольные вопросы.
Контрольные
вопросы
Что называется
стержнем?Какой вид нагружения
стержня называются осевым растяжением
(сжатием)?Как вычисляется
значение продольной силы в произвольном
поперечном сечении стержня?Что такое эпюра
продольных сил и как она строится?Как
распределены нормальные напряжения в
поперечных сечениях центрально-растянутого
или центрально-сжатого стержня, и по
какой формуле они определяются?Что называется
удлинением стержня (абсолютной продольной
деформацией)? Что такое относительная
продольная деформация? Каковы размерности
абсолютной и относительной продольных
деформаций?Что называется
модулем упругости Е? Как влияет величина
Е на деформации стержня?Сформулируйте
закон Гука. Напишите формулы для
абсолютной и относительной продольных
деформаций стержня.Что происходит с
поперечными размерами стержня при его
растяжении (сжатии)?Что такое коэффициент
Пуассона? В каких пределах он изменяется?С
какой целью проводятся механические
испытания материалов? Какие напряжения
являются опасными для пластичных и
хрупких материалов?
Пример выполнения
Построить эпюры
продольных сил и нормальных напряжений
для нагруженного стального бруса (рис.
5.1). Определить удлинение (укорочение)
бруса, если E![]()
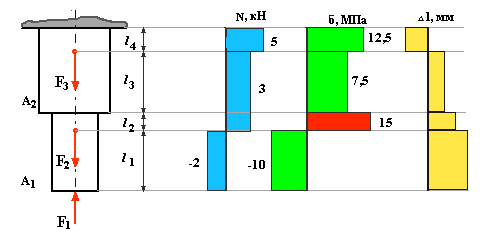
Рис.5.1
Дано: F![]()
= 2 kH,
F![]() =
=
5 kH,
F![]() =
=
2 kH,
A![]() =
=
2 см![]() ,
,
А![]() ,
,
l![]() =
=
100 мм, l![]() =
=
50 мм, l![]() =
=
200 мм,
l![]()
= 150 мм.
Решение. Определяем
продольные силы и строим их эпюру:
N![]() =
=
— F![]() =
=
— 2kH;
N![]() =
=
— F![]() +
+
F![]() =
=
-2 + 5 = 3 kH;
N![]()
= — F![]() +
+
F![]() =
=
3 kH;
N![]()
= — F![]() +
+
F![]() +
+
F![]() =
=
-2 +5 + 2 = 5 kH
Определяем величину
нормальных напряжений и строим их эпюру:
![]()
![]()
![]()
![]()
Используя
видоизмененный закон Гука, определяем
удлинение бруса:
![]()
![]()
![]()
![]()
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
