Построение эпюр перемещений при растяжении
Построение эпюр продольных сил – это решение статически определимой задачи. Производится для выявления картины нагрузки упругого тела. Вернее, уточнения ее схематизации.
Необходимо для определения наиболее напряженного, так называемого «опасного» сечения. Затем методами сопромата (сопротивления материалов) проводится анализ с прогнозированием перемещений элементов конструкции.
Но всему свое время. Сначала немного о терминах.
Основные понятия
Брусом (балкой) называют тело, вытянутое вдоль оси. То есть длина преобладает над шириной и высотой.

Если имеются только осевые (продольные) силы, то объект подвергается растяжению/сжатию. В этом случае в материале возникают только нормальные поперечному сечению силы противодействия и тело считают стержнем.
Статическая определимость подразумевает достаточность схемы для установления внутренних усилий противодействия. Участок – часть балки с неизменным сечением и характерной нагрузкой.
Правила построения учитывают знаки усилий. Растягивающие принимают положительными, сжимающие – отрицательными.
В системе СИ силы измеряются в ньютонах (Н). Длины в метрах (м).
Что такое эпюра продольных сил
Показывает, какой силой (в нашем предположении нормальной) загружен каждый участок. По всей длине стержня. Иначе говоря, эпюра – наглядное графическое изображение изменения нагрузки по всей длине конструкции.
Как построить эпюру продольных сил
Используется метод сечений. Балка виртуально рассекается на каждом участке и ищется противодействующая N. Ведь задача статическая.
Сопротивление рассчитывается по формуле:
где:
Fl – действующие на участке l силы (Н);
ql – распределенные нагрузки (Н/м).
Порядок построения:
1. Рисуется схема балки и механизмов закрепления;
2. Производится разделение на участки;
3. Для каждого рассчитывается N с учетом знаков. Если у балки есть незакрепленный конец, то начинать удобнее именно с него. В противном случае считается реакция опор. И оптимальнее выбирать сечение с меньшим количеством действующих факторов:
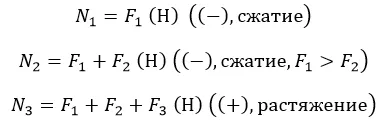
Нетрудно заметить, что последнее уравнение дает еще и реакцию опоры;
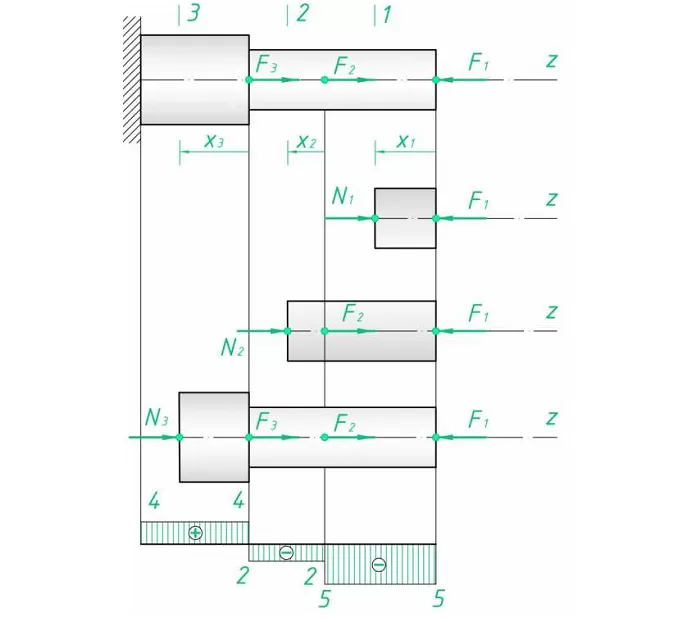
4. Параллельно оси стержня намечается база эпюры. Положительные значения масштабировано проставляются выше, отрицательные – ниже. Эпюру наглядно совмещать с расчетной схемой. Итоговый результат и промежуточные сечения показаны на рис. 1.

Рис. 1. Эпюра продольных сил
Рассмотрим случай:
F1 = 5 (кН);
F2 = 3 (кН);
F3 = 6 (кН).
Вычислим:
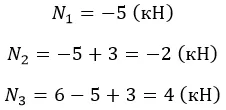
Проверить эпюру можно по скачкам: изменения происходят в точках приложения сил на их величину.
Пример построения эпюр и решения задач
Построить эпюру сил для следующего случая (рис. 2):
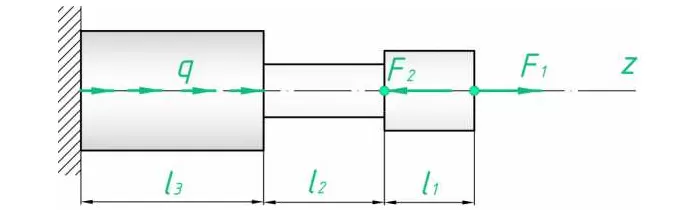
Рис. 2
Дано:
Решение.
Разбиение на участке вполне очевидно. Найдем сопротивление на выделенных:
Распределенная нагрузка зависит от длины, на которой приложена. Поскольку нарастает линейно, значение N2 будет постепенно увеличиваться/уменьшаться в зависимости от знака q.
Эпюра такого вида усилия представляет собой прямоугольный треугольник с катетами l3 и ql3 (в масштабе). Поскольку распределение линейно.
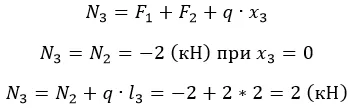
По полученным данным строим эпюру (рис. 3).
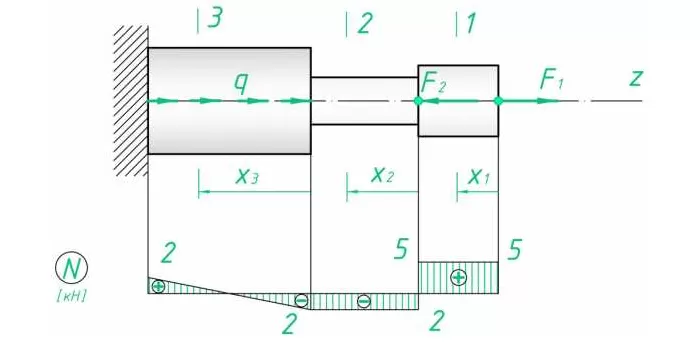
Рис. 3
Заключение
Приведенный алгоритм является предварительным этапом в расчете модели на прочность. «Слабое» место находится уже с учетом площади поперечного сечения.
В сети имеются онлайн сервисы для помощи в расчетах при вычерчивании. Но стоит ли ими пользоваться, если процедура настолько проста? Если не запутаться в знаках, конечно. Это самая распространенная ошибка.
Источник
При растяжении брус удлиняется на А / и сокращается в поперечном сечении на Ah = /г, — И, где h — начальная ширина бруса; И] — ширина бруса после деформации (рис. 2.2.10).
Рис. 2.2.10
Тогда относительная продольная деформация = -j- — ez > 0, а относительная поперечная деформация -h Ah
? = ——-, ? > 0. Опытным путем
у h h у
установлено, что при чистом растяжении или сжатии отношение относительной поперечной деформации к относительной продольной деформации для каждого материала есть величина постоянная.
Это отношение носит название коэффициента поперечной деформации или коэф-
?
фициента Пуассона, р = ——.
ez
Коэффициент Пуассона — это упругая постоянная для данного материала.
Пуассон установил, что коэффициент поперечной деформации для всех материалов р = 0,25, но дальнейшими экспериментальными исследованиями было установлено, что этот коэффициент находится в пределах —0,5
Перемещение произвольного сечения бруса равно изменению длины участка, заключенного между этим сечением и заделкой.
При растяжении (сжатии) бруса его поперечные сечения перемещаются в направлении оси. Перемещения являются следствием деформации. Абсолютная деформация бруса (удлинение или укорочение) равна алгебраической сумме абсолютных деформаций
П
(удлинения или укорочения) отдельных его участков: А/ = ^А/;..
В соответствии с законом Гука А/ = — = о—, складывая абсолютен Е
ные деформации участков, получим
Эпюра перемещения — графическое изображение перемещений поперечных сечений по длине бруса. Эта эпюра строится от заделки, которая принимается за начало координат, так как в заделке перемещение А = 0.
П р и м е р 1. Построить эпюры продольных сил N, нормальных напряжений а и перемещений А для данного стержня (рис. 2.2.11).
Рис. 2.2.11
Дано: 2 105 МПа.
Эпюру продольных сил начинаем строить со свободного конца. Мысленно рассечем брус в сечении I—I и отбросим левую часть, рассмотрим равновесие правой части: = 0; N = F брус растягивается, так как сила F действует от сечения. Продольная сила положительна и на всем участке длиной / постоянна. Нормальные напряжения, как и продольная сила, положительны и постоянны (а = const).
Перемещение сечения, отстоящего от начала координат (заделки) на расстоянии z, равно А(^) = — — это уравнение пря-
ЕЛ
мой, проходящей через начало координат, 0
при z = О А = О,
/ л Nl
прИг = / д = —.
Положительными силами считаются растягивающие, откладываем их на эпюре вверх.
Для эпюры перемещений ординаты откладываются вверх, что соответствует перемещениям сечений слева направо.
Пример 2. Для данного стержня (рис. 2.2.12) построить эпюры продольных сил, нормальных напряжений и перемещений, Е=2105 МПа. 1
Рис. 2.2.12
1. Эпюра продольных сил N.
Строим эпюру со свободного конца — участок КВ. Мысленно рассечем этот участок, отбросив левую часть, и рассмотрим равновесие правой части: = Е— N= О, N= F. Продольная сила N направлена от сечения, следовательно, она положительна, N= 10 кН.
На участке ВС продольная сила N = F. Эпюра продольных сил постоянна по всей длине стержня КС.
2. Эпюра нормальных напряжений о = —.
А
По полученным данным строим эпюру о.
3. Эпюра перемещений А.
Определим, на какую величину переместится сечение на расстоянии z от начала координат (точка С) на участке СВ.
Участок СВ:
при z = О Дс = 0;
, . / 20 Ю2П1
при z = I Дв = свс- = у^- = 0,1см.
Участок ВК:
Пример 3. Для данного стержня построить эпюры продольных сил N, нормальных напряжений о и перемещений А по принципу независимости действия сил (рис. 2.2.13). Все эпюры можно строить по принципу независимости действия сил. Это значит, что каждую эпюру строят от одного внутреннего силового фактора (например, от силы F{), потом от другого (от силы F2), а затем от суммы этих факторов.
Рис. 2.2.13
Дано: Fx = 5 кН; F2 = 10 кН; А = 5 см2; Е = 2 • 105 МПа.
Эпюры продольных сил N.
- 1. Строим эпюру от Fx = 5 кН (считаем, что F2 отсутствует); сила Fx растягивает весь стержень (участки КВ и ВС), поэтому NX=FX = 5 кН.
- 2. Строим эпюру от силы F2 = 10 кН. Сила F2 растягивает только участок ВС, поэтому на участке КВ N2 = 0 и N2 = F2 = 10 кН на участке ВС.
- 3. Строим эпюру от суммы сил Fx и FT Участок КВ: TV , = F. + 0 = 5 кН.
сум 1
Участок ВС: У = F. + F2 = 5 + 10 = 15 кН.
Сум 1 L
Эпюры нормальных напряжений о.
1. Строим эпюру от силы Fy Так как стержень постоянного
Fx 5 103
сечения, то = const на всей длине стержня, о = — —-т —
кс кс л 5 Ш2
= 10 МПа.
2. Строим эпюру от силы FT Участок КВ: о кв = 0, так как N2= 0.
N 10 Ю3
Участок ВС: a Rr — —- =-— = 20 МПа.
к А 5-Ю2
3. Строим эпюру от суммы сил Fx и Fr Участок КВ: акв =10 + 0=10 МПа.
Участок ВС: одс = 10 + 20 = 30 МПа.
Эпюры перемещений А.
1. Строим эпюру от силы Fx.
П a NZ
Для сечения, отстоящего на расстоянии z от заделки, А = — =
ЕА
= акс~’ Так как окс= const, то 0z с = 0; при
M-J
Z= 1 М Ав = 10y~j = 0,005 см; при ^ = 2 м = Ю— = 0,01 см.
2. Строим эпюру от силы FT
гг Л N2Z
Для сечения, отстоящего на расстоянии г от заделки, А = —— =
ЕА
— ®bc^’ 0 z ^ 1 м; при z = 0 Ас = 0; при г = 1 м Ав = авс — = Е Е
= ^ см;на участке КВ акв = 0, поэтому Ак= Ав + 0 =
= 0,01 см.
3. Строим эпюру от суммы сил Fx и F2.
Точка С: Дс = 0.
Точка В: Ав = 0,005 + 0,01 = 0,015 см.
Точка К: Ак= 0,01 + 0,01 = 0,02 см.
Пример 4. Определить диаметр стального стержня (рис. 2.2.14), если под действием нагрузки F= 100 кН удлинение равняется
А/ = 2 мм. Чему будет равна при этом
Рис. 2.2.14
площадь поперечного сечения?
NL
По формуле Гука А/ = —, продоль- ЕЛ
ная сила N во всех сечениях постоянна
и равна 100 кН, /=3м; ?= 2 • 105 МПа;
А — площадь поперечного сечения стержня, А = nd2/4; удлинение стрежня
100-103- 3•103- 4 ,
А/ =—-— = 2 мм = [А/],
2 105 nd2
.. /юо 3 109 4
d > J-т-
2105-л-2
п , _. . 7id2 тс• 31 ^ т
Принимаем d = 31 мм, тогда А ——= 754,36 мм .
5 4
Источник
