Поперечное сужение при растяжении
    Äëÿ îòäåëüíî âçÿòîãî ýëåìåíòà êîíñòðóêöèè âçàèìîóðàâíîâåøåííûå àêòèâíàÿ ñèëà è ñèëà ðåàêöèè îïîðû ÿâëÿþòñÿ
âíåøíèìè ñèëàìè.
    Ðàññìîòðèì, êàêèì îáðàçîì êîíñòðóêöèÿ îêàçûâàåò ñîïðîòèâëåíèå âíåøíåé íàãðóçêå, çà ñ÷åò ÷åãî ïðîèñõîäèò èçìåíåíèå
ôîðìû è ðàçìåðîâ êîíñòðóêöèè — äåôîðìèðîâàíèå (îò ëàò. deformatio — èñêàæåíèå).
10.3.1. Ðàñòÿæåíèå
    Íå îáðàùàÿ âíèìàíèå íà òî, êàêèì îáðàçîì, ñ òî÷êè çðåíèÿ êîíñòðóêòèâíîãî ðåøåíèÿ, ïðèëîæåíû âíåøíèå ñèëû Ð,
ðàññìîòðèì ðàñòÿæåíèå ýëåìåíòà êîíñòðóêöèè, ñõåìà íàãðóæåíèÿ êîòîðîãî ïîêàçàíà íà ðèñ. 10.3,à.
|
Ðèñ. 10.3. Óïðîùåííàÿ ìîäåëü äåôîðìàöèè ïðè ðàñòÿæåíèè |
Íà ðèñ. 10.3 ïîêàçàíà òàêæå óïðîùåííàÿ ìîäåëü ìåæàòîìíûõ ñâÿçåé â òâåðäîì òåëå. Æåñòêèå è ïðî÷íûå ìåæàòîìíûå ñâÿçè, ñîåäèíÿþùèå àòîìû
íåäåôîðìèðîâàííîãî òåëà (ðèñ. 10.3,á), ïðè ðàñòÿæåíèè (ðèñ. 10.3,â) ñîçäàþò áîëüøèå
âíóòðåííèå ñèëû ïðîòèâîäåéñòâèÿ âíåøíåé íàãðóçêå, ñòðåìÿùèåñÿ ñîõðàíèòü òåëî êàê åäèíîå öåëîå.
    Ïîä äåéñòâèåì âíåøíèõ ñèë ÷àñòèöû (àòîìû) ìàòåðèàëà, èç êîòîðîãî ñäåëàíà êîíñòðóêöèÿ, áóäóò ïåðåìåùàòüñÿ, è
ïåðåìåùåíèå ÷àñòèö ïîä íàãðóçêîé áóäåò ïðîäîëæàòüñÿ, ïîêà ìåæäó âíåøíèìè è âíóòðåííèìè ñèëàìè íå óñòàíîâèòñÿ ðàâíîâåñèå.
    Òàêîå ñîñòîÿíèå íàçûâàåòñÿ äåôîðìèðîâàííûì
ñîñòîÿíèåì òåëà.
    Ìåðîé âîçäåéñòâèÿ âíåøíèõ ñèë íà àòîìû âåùåñòâà, êîòîðûå óäàëÿþòñÿ äðóã îò äðóãà (ïðè ðàñòÿæåíèè) èëè ñáëèæàþòñÿ
(ïðè ñæàòèè), ò. å. ìåðîé ïðîòèâîäåéñòâèÿ ìàòåðèàëà êîíñòðóêöèè âíåøíåìó ñèëîâîìó âîçäåéñòâèþ, ìåðîé âíóòðåííèõ ñèë â ìàòåðèàëå ÿâëÿåòñÿ
íàïðÿæåíèå. Íàïðÿæåíèåì íàçûâàåòñÿ âíóòðåííÿÿ ñèëà (âîçíèêàþùàÿ ïðè âîçäåéñòâèè âíåøíåé íàãðóçêè),
ïðèõîäÿùàÿñÿ íà åäèíèöó ïëîùàäè â îêðåñòíîñòè äàííîé òî÷êè ðàññìàòðèâàåìîãî ñå÷åíèÿ òåëà:
σ = Ð/F,
| ãäå    | σ |    - | íàïðÿæåíèå, Ïà (1Ïà=1Í/ì2); |
| P |    - | ñóììàðíàÿ ñèëà, Í; | |
| F |    - | ïëîùàäü ïîïåðå÷íîãî ñå÷åíèÿ, ïåðïåíäèêóëÿðíîãî íàïðàâëåíèþ äåéñòâóþùåé ñèëû P,ì2. |
   Â èíæåíåðíîé ïðàêòèêå èíîãäà èçìåðÿþò íàïðÿæåíèÿ â äàÍ/ìì2 (1äàÍ= 10Í).
   Íàïðÿæåíèå, òàêèì îáðàçîì, ïîêàçûâàåò èíòåíñèâíîñòü ïðîòèâîäåéñòâèÿ âíóòðåííèõ ñèë âîçäåéñòâèþ âíåøíåé íàãðóçêè íà
ìåæàòîìíûå ñâÿçè ìàòåðèàëà êîíñòðóêöèè, èëè, ÷òî òî æå ñàìîå, èíòåíñèâíîñòü âîçäåéñòâèÿ âíåøíåé íàãðóçêè íà ìåæàòîìíûå ñâÿçè.
   Åñëè ðàññìîòðåòü äåôîðìèðîâàííîå ñîñòîÿíèå ñòåðæíÿ (áðóñà) (ðèñ. 10.4) ïðè ðàñòÿæåíèè âíåøíèìè ñèëàìè Ð
(ïîêàçàíû íà ðèñóíêå ÷åðíûìè ñòðåëêàìè), òî â ëþáîì ïðîèçâîëüíî âçÿòîì ïîïåðå÷íîì ñå÷åíèè (íàïðèìåð, ïëîñêîñòüþ À) ðàñïðåäåëåíèå
íîðìàëüíûõ íàïðÿæåíèé σ = Ð/F áóäåò ðàâíîìåðíûì.
|
Ðèñ. 10.4. Äåôîðìèðîâàííîå ñîñòîÿíèå áðóñà |
   Ðàâíîäåéñòâóþùàÿ ñèëà íàïðÿæåíèé σ — âíóòðåííÿÿ ñèëà
Ð = σF (íà ðèñ. 10.4 — áåëàÿ ñòðåëêà) — ïðîõîäèò ÷åðåç öåíòð òÿæåñòè ïîïåðå÷íîãî ñå÷åíèÿ âäîëü ëèíèè äåéñòâèÿ
âíåøíåé ñèëû è ðàâíà åé.
   Ïîä äåéñòâèåì ðàñòÿãèâàþùèõ ñèë Ð äëèíà ñòåðæíÿ l óâåëè÷èâàåòñÿ íà âåëè÷èíó Δl,
íàçûâàåìóþ àáñîëþòíûì óäëèíåíèåì. Ðàñòÿæåíèå ñîïðîâîæäàåòñÿ òàêæå óìåíüøåíèåì ïîïåðå÷íûõ ðàçìåðîâ
ñå÷åíèÿ. Ýòî ÿâëåíèå íîñèò íàçâàíèå «ýôôåêò Ïóàññîíà» (ïî èìåíè ôðàíöóçñêîãî ó÷åíîãî è ìåõàíèêà
Ñ. Ïóàññîíà). Àáñîëþòíîå ïîïåðå÷íîå ñóæåíèå
ñòåðæíÿ ïðè ðàñòÿæåíèè Δb =
b — b1; Δc = c — c1.
   Èìåííî çà ñ÷åò èçìåíåíèÿ ôîðìû è ðàçìåðîâ ëþáàÿ êîíñòðóêöèÿ ñîïðîòèâëÿåòñÿ (ñîçäàåò ñèëû ïðîòèâîäåéñòâèÿ) âíåøíèì íàãðóçêàì.
   Â èíæåíåðíîé ïðàêòèêå äåôîðìèðîâàííîå ñîñòîÿíèå ïðèíÿòî îöåíèâàòü íå òîëüêî àáñîëþòíûìè âåëè÷èíàìè èçìåíåíèé ôîðìû
( «ïåðåìåùåíèÿìè»), íî è îòíîñèòåëüíûìè áåçðàçìåðíûìè âåëè÷èíàìè —
«äåôîðìàöèÿìè»:
ε = Δl/l; ε = Δb/b = Δc/c,
| ãäå    | ε |    - | îòíîñèòåëüíîå óäëèíåíèå ïðè ðàñòÿæåíèè; |
| ε’ |    - | îòíîñèòåëüíûå ïîïåðå÷íûå äåôîðìàöèè. |
   Ïðè äîñòàòî÷íî áîëüøèõ âíåøíèõ íàãðóçêàõ (è, êàê ñëåäñòâèå, áîëüøèõ âíóòðåííèõ íàïðÿæåíèÿõ) ìåæàòîìíûå ñâÿçè ìàòåðèàëà ìîãóò
áûòü ðàçîðâàíû, ÷òî ïðèâåäåò ê ðàçðóøåíèþ êîíñòðóêöèè.
   Êîíñòðóêöèÿ äîëæíà áûòü ñïðîåêòèðîâàíà òàê, ÷òîáû îíà íå ðàçðóøèëàñü ïîä íàãðóçêîé. Äåôîðìàöèè (ïåðåìåùåíèÿ), êîòîðûå
íåèçáåæíî âîçíèêàþò â êîíñòðóêöèè ïîä íàãðóçêîé, äîëæíû áûòü âïîëíå îïðåäåëåííûìè è äîñòàòî÷íî ìàëûìè, ïîñêîëüêó âûáðàííûå ðàçìåðû è ôîðìà
ýëåìåíòîâ êîíñòðóêöèè îáåñïå÷èâàþò îïðåäåëåííîå êà÷åñòâî åå ôóíêöèîíèðîâàíèÿ.
   Òàê, èçìåíåíèå ïîä íàãðóçêîé ðàçìåðîâ è ôîðìû ýëåìåíòîâ êîíñòðóêöèè ñàìîëåòà, îáòåêàåìûõ ïîòîêîì âîçäóõà, ñóùåñòâåííûì îáðàçîì
âëèÿåò íà àýðîäèíàìè÷åñêèå õàðàêòåðèñòèêè è, êàê ñëåäñòâèå, — íà ëåòíî-òåõíè÷åñêèå õàðàêòåðèñòèêè ñàìîëåòà.
   Õàðàêòåð ðàáîòû êîíñòðóêöèè ïîä íàãðóçêîé âî ìíîãîì îïðåäåëÿåòñÿ âûáîðîì êîíñòðóêöèîííûõ
ìàòåðèàëîâ. Îäíîé èç îñíîâíûõ õàðàêòåðèñòèê ìàòåðèàëà êîíñòðóêöèè ÿâëÿåòñÿ äèàãðàììà ðàñòÿæåíèÿ (êðèâàÿ äåôîðìèðîâàíèÿ) — âçàèìîçàâèñèìîñòü íàïðÿæåíèé è äåôîðìàöèé
óäëèíåíèÿ, ïîëó÷àåìàÿ â ðåçóëüòàòå èñïûòàíèé îáðàçöîâ ìàòåðèàëîâ íà ðàñòÿæåíèå. Íà ðèñ. 10.5 ïîêàçàí òèïè÷íûé õàðàêòåð äèàãðàìì ðàñòÿæåíèÿ äëÿ
íåêîòîðûõ êîíñòðóêöèîííûõ ìàòåðèàëîâ, ïðèìåíÿåìûõ â ñàìîëåòîñòðîåíèè.
|
Ðèñ. 10.5. Äèàãðàììà ðàñòÿæåíèÿ |
   Ïðÿìîëèíåéíûå íà íåêîòîðîì ïðîòÿæåíèè äèàãðàììû ó÷àñòêè (0-À, 0-ÀÂ) õàðàêòåðèçóþò òàêóþ ñòàäèþ äåôîðìèðîâàíèÿ îáðàçöà,
êîãäà ïðè óâåëè÷åíèè íàãðóçêè äåôîðìàöèè ïðîïîðöèîíàëüíû íàïðÿæåíèÿì è ïðè ñíÿòèè íàãðóçêè èñ÷åçàþò, ò. å. îáðàçåö çà ñ÷åò ìåæàòîìíûõ ñâÿçåé
(ñèë óïðóãîñòè) âîçâðàùàåòñÿ â èñõîäíîå (íåäåôîðìèðîâàííîå) ñîñòîÿíèå. Íà ýòîì ó÷àñòêå ìàòåðèàë «ïîä÷èíÿåòñÿ»
çàêîíó Ãóêà (ïî èìåíè àíãëèéñêîãî åñòåñòâîèñïûòàòåëÿ
Ð. Ãóêà):
σ = Åε,
| ãäå    | σ |    - | íàïðÿæåíèå, Ïà; |
| E |    - | ìîäóëü óïðóãîñòè ìàòåðèàëà, èëè ìîäóëü Þíãà (ïî èìåíè àíãëèéñêîãî ó÷åíîãî Ò.Þíãà), Ïà; | |
| ε |    - | îòíîñèòåëüíîå óäëèíåíèå. |
   Ìîäóëü óïðóãîñòè Å (íàêëîí êðèâîé äåôîðìèðîâàíèÿ â çîíå óïðóãîñòè
0-À (0-ÀÂ) äèàãðàììû: Å = tgα) ÿâëÿåòñÿ ìåðîé óïðóãîñòè («æåñòêîñòè») è õàðàêòåðèçóåò ïîäàòëèâîñòü (ñïîñîáíîñòü ê
äåôîðìèðîâàíèþ) ïîä íàãðóçêîé. Îòìåòèì, ÷òî ñòàëü — áîëåå æåñòêèé, ìåíåå ïîäàòëèâûé ìàòåðèàë, ÷åì àëþìèíèåâûé ñïëàâ.
   Òî÷êà À (ÀÂ) íà äèàãðàììàõ õàðàêòåðèçóåò íàèáîëüøóþ íàãðóçêó Ðïö è, ñîîòâåòñòâåííî,
íàïðÿæåíèÿ
ïðåäåëà ïðîïîðöèîíàëüíîñòè
σïö, ïðè êîòîðûõ åùå ñîáëþäàåòñÿ ëèíåéíàÿ
çàâèñèìîñòü σ — ε.
   Äàëüøå, çà òî÷êîé À (ÀÂ), ëèíåéíàÿ çàâèñèìîñòü σ — ε íàðóøàåòñÿ, ìàòåðèàë äåôîðìèðóåòñÿ («òå÷åò»)
ïîä íàãðóçêîé è ïðè ñíÿòèè íàãðóçêè íå âîçâðàùàåòñÿ ê èñõîäíîìó ñîñòîÿíèþ, â íåì âîçíèêàþò îñòàòî÷íûå ïëàñòè÷åñêèå
äåôîðìàöèè çà ñ÷åò òîãî, ÷òî ÷àñòü ìåæàòîìíûõ ñâÿçåé ðàçðóøàåòñÿ. Òî÷êà  íà äèàãðàììàõ õàðàêòåðèçóåò íàãðóçêó
Ðò è, ñîîòâåòñòâåííî,
íàïðÿæåíèÿ ïðåäåëà òåêó÷åñòè
σò, ïðè êîòîðûõ ìàòåðèàë «òå÷åò» áåç óâåëè÷åíèÿ íàãðóçêè. Íåêîòîðûå ìàòåðèàëû (íàïðèìåð, 4, ñì. ðèñ. 10.5)
èìåþò ÿâíî âûðàæåííóþ ïëîùàäêó òåêó÷åñòè À-Â, ãäå äåôîðìàöèè ñóùåñòâåííî óâåëè÷èâàþòñÿ áåç óâåëè÷åíèÿ
âíåøíåé íàãðóçêè. Äëÿ äðóãèõ ìàòåðèàëîâ (1, 2, 3) ïëîùàäêè òåêó÷åñòè îòñóòñòâóþò, â ýòîì ñëó÷àå òî÷êè À è  íà äèàãðàììå ïðàêòè÷åñêè
ñîâïàäàþò.
   Çîíà Â-Ñ äèàãðàììû íàçûâàåòñÿ çîíîé óïðî÷íåíèÿ. Çäåñü ïîñëå ñòàäèè òåêó÷åñòè
ìàòåðèàë ñíîâà ïðèîáðåòàåò ñïîñîáíîñòü óâåëè÷èâàòü ñîïðîòèâëåíèå äàëüíåéøåé äåôîðìàöèè, îäíàêî äëÿ óäëèíåíèÿ îáðàçöà â ýòîé çîíå òðåáóåòñÿ â
ñîòíè ðàç áîëåå ìåäëåííîå íàðàñòàíèå íàãðóçêè, ÷åì â çîíå óïðóãèõ äåôîðìàöèé.
|
Ðèñ. 10.6. Äèàãðàììà èñòèííûõ íàïðÿæåíèé |
   Òî÷êà Ñ äèàãðàììû õàðàêòåðèçóåò ìàêñèìàëüíóþ (ïðåäåëüíóþ) íàãðóçêó Ðmax è, ñîîòâåòñòâåííî,
íàïðÿæåíèÿ ïðåäåëà ïðî÷íîñòè èëè íàïðÿæåíèÿ âðåìåííîãî ñîïðîòèâëåíèÿ σâ, ïðè êîòîðûõ åùå ñîõðàíÿåòñÿ öåëîñòíîñòü
ýëåìåíòà êîíñòðóêöèè, íàãðóæåííîãî ðàñòÿæåíèåì.
   Äàëüøå, çà òî÷êîé Ñ äèàãðàììû, áåç óâåëè÷åíèÿ âíåøíåé íàãðóçêè èäåò ëàâèíîîáðàçíîå ðàçðóøåíèå ìåæàòîìíûõ ñâÿçåé
ìàòåðèàëà.
   Íàïðÿæåíèå σâ, òàêèì îáðàçîì, õàðàêòåðèçóåò ïðî÷íîñòü ìàòåðèàëà íà ðàçðûâ.
   Òî÷êà D äèàãðàììû õàðàêòåðèçóåò ðàçðóøåíèå (ðàçðûâ) îáðàçöà. Íèñõîäÿùàÿ âåòâü äèàãðàììû Ñ-D èìååò óñëîâíûé
õàðàêòåð, ïîñêîëüêó íàïðÿæåíèÿ ðàññ÷èòûâàþòñÿ äëÿ ïëîùàäè ïîïåðå÷íîãî ñå÷åíèÿ èñõîäíîãî îáðàçöà. Ðåàëüíî íàïðÿæåíèÿ ðàñòóò, ÷òî ïîêàçûâàåò
äèàãðàììà èñòèííûõ íàïðÿæåíèé (ðèñ. 10.6 — ïóíêòèðíàÿ ëèíèÿ),
â êîòîðîé íàïðÿæåíèÿ ðàññ÷èòûâàþòñÿ äëÿ èñòèííîé ïëîùàäè ïîïåðå÷íîãî ñå÷åíèÿ îáðàçöà.  èíòåðâàëå Î-À ðîñò íàïðÿæåíèÿ èäåò áåç
ðàçðóøåíèÿ ìåæàòîìíûõ ñâÿçåé, ïîñëå ñíÿòèÿ íàãðóçêè îáðàçåö âîçâðàùàåòñÿ ê èñõîäíîìó ñîñòîÿíèþ. Â èíòåðâàëå À-D ðîñò íàïðÿæåíèÿ
ïðîèñõîäèò çà ñ÷åò ðàçðóøåíèÿ ìåæàòîìíûõ ñâÿçåé è çíà÷èòåëüíîãî ìåñòíîãî óòîíåíèÿ îáðàçöà (îáðàçîâàíèÿ
øåéêè 1).  ìîìåíò ðàçðóøåíèÿ (òî÷êà D äèàãðàììû) ïëîùàäü ïîïåðå÷íîãî ñå÷åíèÿ ïëàñòè÷åñêè
äåôîðìèðîâàííîãî îáðàçöà ìåíüøå èñõîäíîé.
   Ïðî÷íîñòü êîíñòðóêöèè, åñòåñòâåííî, çàâèñèò îò ïðî÷íîñòè ìàòåðèàëà, èç êîòîðîãî îíà èçãîòîâëåíà.
   Ïðî÷íîñòü
(íåñóùàÿ ñïîñîáíîñòü)
êîíñòðóêöèè — ýòî ñïîñîáíîñòü êîíñòðóêöèè â îïðåäåëåííûõ óñëîâèÿõ âîñïðèíèìàòü (âûäåðæèâàòü) áåç
ðàçðóøåíèÿ âíåøíèå íàãðóçêè.
Íàãðóçêà, ïðè êîòîðîé ïðîèñõîäèò ðàçðóøåíèå êîíñòðóêöèè, íàçûâàåòñÿ
ðàçðóøàþùåé.
|
Ðèñ. 10.7. Òðàåêòîðèè íàïðÿæåíèé |
   Íåñóùàÿ ñïîñîáíîñòü âî ìíîãîì çàâèñèò îò ïëàñòè÷íîñòè ìàòåðèàëà. Ïëàñòè÷íîñòü
— ñïîñîáíîñòü ìàòåðèàëà ïîëó÷àòü áîëüøèå îñòàòî÷íûå äåôîðìàöèè, íå ðàçðóøàÿñü. Õðóïêîñòü
(ñâîéñòâî, ïðîòèâîïîëîæíîå ïëàñòè÷íîñòè) — ñïîñîáíîñòü ìàòåðèàëà ðàçðóøàòüñÿ áåç çàìåòíîé ïëàñòè÷åñêîé äåôîðìàöèè.
   Æåñòêîñòü — ñïîñîáíîñòü êîíñòðóêöèè ñîïðîòèâëÿòüñÿ äåéñòâèþ âíåøíèõ íàãðóçîê
ñ äîïóñòèìûìè â ýêñïëóàòàöèè äåôîðìàöèÿìè, íå íàðóøàþùèìè ðàáîòîñïîñîáíîñòü êîíñòðóêöèè.
   Íåñóùàÿ ñïîñîáíîñòü êîíñòðóêöèè ðåçêî ñíèæàåòñÿ èìåþùèìèñÿ â ìàòåðèàëå êîíñòðóêöèè ìèêðîòðåùèíàìè, âêðàïëåíèÿìè
èíîðîäíûõ ìàòåðèàëîâ, íàðóøàþùèìè ïîñòîÿíñòâî íàïðÿæåíèé.
   Êîíöåíòðàòîðû íàïðÿæåíèé
— ìåñòíûå ðåçêèå èçìåíåíèÿ îäíîðîäíîñòè (ôîðìû è, ñëåäîâàòåëüíî, æåñòêîñòè) êîíñòðóêöèè, ïðèâîäÿùèå ê ðåçêîìó ìåñòíîìó
(ëîêàëüíîìó) ïîâûøåíèþ íàïðÿæåíèé â êîíñòðóêöèè.
   Íà ðèñ. 10.7 ïîêàçàíî äåéñòâèå ðàñòÿãèâàþùåé âíåøíåé íàãðóçêè, ðàâíîìåðíî ðàñïðåäåëåííîé ïî êðàÿì ïðîñòåéøèõ êîíñòðóêòèâíûõ
ýëåìåíòîâ — ëèñòîâ. Ïóíêòèðíûå ëèíèè ïðåäñòàâëÿþò ñîáîé òàê íàçûâàåìûå òðàåêòîðèè íàïðÿæåíèé, âäîëü êîòîðûõ íàïðÿæåíèå ïåðåäàåòñÿ îò
ìîëåêóëû ê ìîëåêóëå. Äëÿ ãëàäêîãî ëèñòà ýòè ëèíèè ïàðàëëåëüíû, íàïðÿæåíèÿ â ëþáîì ñå÷åíèè ëèñòà îäèíàêîâû.
|
Ðèñ. 10.8. ïåðåäà÷à íàãðóçêè â ñîåäèíåíèè |
   Ñèëû, ïåðåäàþùèåñÿ ïî òðàåêòîðèÿì íàïðÿæåíèé â ëèñòàõ ñ êîíöåíòðàòîðàìè (íàäðåç â êðîìêå ëèñòà, îòâåðñòèå â öåíòðå ëèñòà),
îáõîäÿò ðàçðûâ â ìàòåðèàëå. Ïëîòíîñòü òðàåêòîðèé íàïðÿæåíèé óâåëè÷èâàåòñÿ, è ëîêàëüíûå íàïðÿæåíèÿ σ ó êðàÿ êîíöåíòðàòîðà âîçðàñòàþò
(èíîãäà ìíîãîêðàòíî). Â ýòèõ ìåñòàõ ìîæåò ïðîèçîéòè íàðóøåíèå (ðàçðûâ) ìåæàòîìíûõ ñâÿçåé, âîçíèêíóò ìèêðîòðåùèíû, ðàñïðîñòðàíåíèå êîòîðûõ âåäåò
ê ðàçðóøåíèþ êîíñòðóêöèè.
   Ðàñïðåäåëåíèå íàïðÿæåíèé â çàêîíöîâêàõ (ìåñòàõ ñîåäèíåíèÿ äåòàëåé)
îáû÷íî îñîáåííî
ñëîæíî, â íèõ îáÿçàòåëüíî ïîÿâëÿþòñÿ êîíöåíòðàöèè íàïðÿæåíèé
— ìåñòíîå ïîâûøåíèå íàïðÿæåíèé.
   Â ìåñòå ñîåäèíåíèÿ (ðèñ. 10.8) ëèñòîâ 1 è 3 ñ ïîìîùüþ çàêëåïîê (èëè ñâàðíûõ òî÷åê) 2 ïåðåäà÷à
íàãðóçêè áóäåò
ïðîèñõîäèòü òîëüêî ÷åðåç òî÷êè êðåïëåíèÿ. Ëèñòû ðàâíîìåðíî âêëþ÷àòñÿ â ðàáîòó íà äîñòàòî÷íî áîëüøîì óäàëåíèè îò ìåñòà
ñîåäèíåíèÿ.
   Çàøòðèõîâàííàÿ îáëàñòü ëèñòîâ ïðàêòè÷åñêè âûêëþ÷åíà èç ðàáîòû è íå èñïûòûâàåò íàïðÿæåíèé.  òî æå âðåìÿ
íàïðÿæåíèÿ â ïîïåðå÷íûõ ñå÷åíèÿõ ëèñòîâ ðàñïðåäåëåíû íåðàâíîìåðíî, ïðè÷åì σÀ-À > σÁ-Á > σÂ-Â.
   Êîíñòðóêòîð îñîáîå âíèìàíèå äîëæåí óäåëÿòü âûáîðó ôîðìû äåòàëåé, ðàáîòàþùèõ íà ðàñòÿæåíèå, è îñîáåííî èõ
çàêîíöîâîê, ÷òîáû óìåíüøèòü âîçìîæíûå êîíöåíòðàöèè íàïðÿæåíèé.
Источник
Продольная деформация при растяжении образцов.
Продольная деформация образца при растяжении, как уже указывалось, определяется по формуле (3)
Деформация измеряется тензометрами или оптическим методом (рис. 4.8).
Рис. 4.7. Испытания на твердость по Роквеллу и по Бринелю
Поперечная деформация, коэффициент Пуассона.
Измерения показывают, что при растяжении происходит не только увеличение длины образца, но и уменьшение его поперечных размеров.
Деформация в поперечном направлении
где d — диаметр цилиндрической части образца после растяжения. Экспериментально установлено, что при упругих деформациях
где — коэффициент Пуассона (постоянная материала).
Для большинства конструктивных материалов . Объемная деформация при растяжении
где первоначальный объем материала Учитывая соотношения (11) — (13), найдем при упругих деформациях
Пренебрегая малыми членами, получим следующее значение объемной деформации при растяжении:
Из физических соображений очевидно, что при растяжении объем материала не должен уменьшаться, и потому
Для изотропного материала коэффициент Пуассона должен лежать в пределах — .
Отрицательная нижняя граница связана с энергетическими соображениями, рассмотрение которых опускаем.
Практически отсутствуют материалы, имеющие отрицательное значение коэффициента Пуассона, и потому следует считать
Замечание. В принципе отрицательные значения т. е. увеличение поперечных размеров при растяжении, могут иметь место, если процесс деформирования сопровождается обратимыми физико-химическими изменениями.
Рис. 4.8. Измерение деформаций с помощью тензометров или оптическим методом
Коэффициент Пуассона в упругопластической стадии.
Соотношение (12) справедливо и при появлении пластических деформаций, но при этом значение становится зависящим от величины деформации:
При возрастании деформации и появлении значительных пластических деформаций
Экспериментально установлено, что пластическая деформация протекает без изменения объема материала. Последнее обстоятельство становится физически понятным, если учесть, что деформация пластичности образуется за счет сдвига слоев материала.
Относительное удлинение при разрыве.
Важной характеристикой пластичности материала является остаточное (относительное) удлинение при разрыве. На рис. 4.9 показан образец до и после разрушения.
Для простого измерения удлинения на образец предварительно наносят две риски на расстоянии ; после деформации определяют расстояние между рисками складывая вместе две половинки образца;
остаточное удлинение принято измерять в процентах.
Так как после образования шейки удлинение материала происходит только в этом районе, то величина зависит от соотношения длины и диаметра образца. Для стандартных образцов применяют и соответственно обозначают удлинение при разрыве
Расположение сечения разрыва на образце в его цилиндрической части может быть случайным, связанным с некоторыми нарушениями однородности свойств материала по длине.
Рис. 4.9. Измерение удлинения образца и диаметра шейки при обрыве
Рис. 4.10. Диаграммы деформирования для пластичного (а) и хрупкого (б) материалов
Если обрыв произошел в сечении, близком к головке, то развитие пластической деформации в шейке было затруднено и значение получилось заниженным. В подобных случаях либо повторяют испытание, либо используют для оценки ту часть образца, а которой пластическая деформация не была стеснена.
Пластичные и хрупкие материалы при испытаниях на растяжение.
На рис. 4.10 показаны диаграммы деформирования для пластичных и хрупких материалов.
Материалы, обладающие к моменту разрушения значительной величиной , называются пластичными. Значения для некоторых конструкционных материалов приведены в табл. 1. Материалы, для которых остаточное удлинение меньше 3%, относят к хрупким материалам. Для элементов конструкций в подавляющем большинстве случаев необходимо применять достаточно пластичные материалы.
Пластичные материалы обладают способностью повышенного сопротивления в условиях концентрации напряжений, ударных к тепловых воздействий, при наличии трещин и поверхностных повреждений и т. п.
Материалы с высокими характеристиками прочности часто не могут использоваться в конструкциях, если они являются хрупкими. Малейший поверхностный дефект в виде риски, царапины приводит к значительной потере прочности (достаточно привести пример резки стекла). Часто хрупкие материалы очень сложны в производстве, так как не позволяют использовать сварку, клепку, рихтовку, правку, не выдерживают перенапряжения при монтаже и т. п.
Замечание. Не следует считать, что в современной технике невозможно применение малопластичных материалов. Широкое использование жаропрочных литых материалов для лопаток турбин опровергает такое мнение. При правильном проектировании (в первую очередь, если исключены концентраторы напряжений и работа на растяжение) могут оказаться работоспособными конструкционное материалы с удлинением при разрыве в пределах 0,5—3%.
Относительное сужение поперечного сечения при разрыве.
Второй важной характеристикой пластичности материала является сужение поперечного сечения образца при разрыве:
где — первоначальная площадь поперечного сечения образца, FK — конечная площадь сечения в шейке образца после разрушения:
где — диаметр шейки образца.
Обычно величину которую называют поперечным сужением, измеряют в процентах.
Рис. 4.11. Деформация материалов в зоне шейки
Величина как характеристика пластичности имеет преимущество по сравнению с величиной — удлинением при разрыве, так как не зависит от геометрической формы цилиндрического образца (отношения ).
Естественно, что поперечное сужение связано с максимальной деформацией растяжения в шейке образца. Эту связь можно установить, принимая, что пластическая деформация протекает без изменения объема.
Рассмотрим слой материала образца толщиной (рис. 4.11), который в момент разрушения оказался в зоне шейки. Из условия постоянства объема находим
Учитывая равенства
где — относительное удлинение материала образца в зоне шейки, — поперечное сужение, получим
Из последнего соотношения вытекает
Следует отметить, что существенно больше , так как выражает местную, а не среднюю деформацию на длине .
Для большинства материалов
Источник
ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ
ЦЕНТРАЛЬНЫЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ
ИНСТИТУТ
СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ
им. В.А. КУЧЕРЕНКО ГОССТРОЯ СССР
РЕКОМЕНДАЦИИ
ПО МЕТОДИКЕ ОПРЕДЕЛЕНИЯ
ОТНОСИТЕЛЬНОГО РАВНОМЕРНОГО
УДЛИНЕНИЯ СТРОИТЕЛЬНЫХ
СТАЛЕЙ ПРИ ИСПЫТАНИИ
НА РАСТЯЖЕНИЕ
Утверждены директором ЦНИИСК
им. В.А.
Кучеренко
27 апреля 1979 г.
МОСКВА — 1980
Рекомендации распространяются
на стальной
прокат для строительных металлических
конструкций и устанавливают методы определения относительного равномерного
удлинения как характеристики, нормируемой
техническими условиями, так и необходимой при
проведении научно-исследовательских работ.
Рекомендации предназначены
для инженерно-технических работников заводских
лабораторий (заводов строительных металлоконструкций)
и научно-исследовательских организаций.
Рис. 2.
СОДЕРЖАНИЕ
При работе стали в
конструкциях характеристика относительного равномерного удлинения играет важную роль для
оценки способности металла пластически деформироваться. Эта характеристика
имеет большее значение, чем нормируемое в настоящее время полное относительное
удлинение согласно ГОСТ 1497-73. До настоящего времени для определения равномерного
относительного удлинения в основном использовалась методика, описанная в
стандарте на арматурные стали, где не предусмотрены плоские образцы.
Настоящее руководство
распространяется на стальной толстолистовой, широкополосный универсальный и
фасонный (уголок, швеллер, балка) прокат толщиной от 4 до 40 мм, независимо от
его прочностных свойств, предназначенный для изготовления
строительных металлических конструкций, и
устанавливает методы определения относительного равномерного удлинения при
статических испытаниях
на растяжение при нормальных температурах ![]() .
.
Применение методов
определения относительного равномерного удлинения предусматривается в
стандартах и технических условиях на соответствующие виды проката,
предназначенного для строительных металлических конструкций.
Термины и определения,
принятые в настоящих рекомендациях, согласованы с ГОСТ 1497-73 «Металлы. Методы испытания на растяжение».
Относительное равномерное
удлинение определяется одновременно с относительным удлинением после разрыва.
Настоящие рекомендации
разработаны Отделением прочности и новых форм металлических конструкций и
Отделением испытаний конструкций ЦНИИСК им. Кучеренко Госстроя СССР (составили кандидаты
технических наук Потапов В.Н. и Жулев Ю.К.) на
основании материалов исследований, выполненных
в период 1976-78 гг.
Дирекция ЦНИИСК
им. Кучеренко
1.1. При испытании на
растяжение по определению относительного равномерного удлинения принимаются
следующие обозначения и определения:
l — рабочая длина в мм — часть образца с постоянной площадью поперечного сечения между его
головкой или участком для захвата;
l0 — начальная расчетная длина образца в мм, на которой
определяется удлинение после разрыва;
lпр — начальная расчетная длина участка образца в мм, на которой
определяется равномерное удлинение;
lкр — конечная расчетная длина участка образца в мм, не
включающая место разрыва;
lт — установочная база измерителя деформаций в мм;
d0 — начальный диаметр рабочей части цилиндрического образца до
разрыва в мм;
F0 — начальная площадь поперечного сечения рабочей части образца в мм2;
Fкр — конечная площадь поперечного сечения рабочей части образца после
разрыва, определяемая в расчетной части равномерного
относительного удлинения в мм2.
1.2. Характеристики
механических свойств, получаемых при испытании на растяжение, имеют следующие
обозначения и определения:
δр — относительное равномерное удлинение после разрыва в % — отношение приращения расчетной длины образца (lкр — lнр) на участке, не
включающем место разрыва, к соответствующей первоначальной длине lнр;
ψp — относительное равномерное сужение в % — отношение изменения
площади поперечного сечения образца (F0 — Fкр) после разрыва на участке, не включающем место разрыва, к начальной площади поперечного сечения;
Pвр — максимальная осевая растягивающая нагрузка в кГс, действующая
на образец до образования шейки.
2.1. Для определения
относительного равномерного удлинения при испытании на растяжение применяют
пропорциональные плоские образцы типов I и II с начальной расчетной длиной ![]() а также пропорциональные цилиндрические образцы типов I — VII
а также пропорциональные цилиндрические образцы типов I — VII
с l0 = 10d0 по ГОСТ 1497-73.
2.2. Рабочая длина плоского
образца должна составлять
![]()
2.3. При испытании
толстолистового широкополосного и уголкового проката применяют, как правило, плоские образцы. При
испытании швеллерного и двутаврового проката применяют, в основном,
цилиндрические образцы; допускается применение плоских образцов с одной прокатной и другой
обработанной поверхностями.
Плоские образцы должны сохранять
поверхностные слои проката. При толщине проката свыше 25 мм:
— испытания проводят на
плоских образцах толщиной 25 мм с одной прокатной поверхностью;
— допускается применять
плоские образцы
с обеими прокатными поверхностями, принимая при этом ширину образца не менее 50
мм и расчетную длину ![]() .
.
2.4. Измерение начальной и
конечной расчетных длин, размеров поперечного
сечения образца производят с точностью до 0,1 мм.
2.5. На рабочей части образца
рекомендуется наносить разметку — неглубокие керны, риски или иные метки через каждые 5 или
10 мм.
3.1. Для испытаний применяют
разрывные и универсальные машины всех систем, если они соответствуют
требованиям ГОСТ 1497-73, ГОСТ 7855-74
и требованиям
стандартов на стали для строительных металлических конструкций.
3.2. При проведении испытаний
должны соблюдаться следующие основные условия:
а) надежное центрирование
образца в захватах испытательной машины;
б) плавность нагружения;
в) скорость перемещения активного захвата при
испытании до предела текучести долина быть не
более 0,01, за пределом текучести не более 0,2 длины расчетной части образца,
выраженной в мм/мин.
4.1. При текущих испытаниях
определение относительного равномерного
удлинения может производиться по одному из
следующих методов:
Первый метод
Относительное равномерное
удлинение δр определяют вне участка разрыва (предпочтительней на
большей части разрушенного образца) на начальной расчетной длине, равной 50 мм.
При этом расстояние от места разрыва до
ближайшей точки (риски) начальной расчетной
длины lпр должно быть не менее 3b0*) (с округлением до ближайшей удаленной
разметочной риски от места разрыва образца где
b0 — начальная ширина образца (рис. 1).
______________
*)
В случае цилиндрических образцов вместо b0 следует d0.
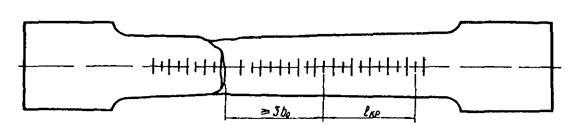
Рис. 1
Относительное равномерное
удлинение δр в процентах вычисляют по формуле
![]()
Второй метод
Относительное равномерное
удлинение δр в % вычисляют по следующей формуле
![]()
где ψр — относительное равномерное сужение в %, вычисленное по формуле
![]()
Измерение площади Fкр производится на расстоянии от места
разрыва не менее 4b0.
Третий метод*)
______________
*) Этот метод
допускает использование образцов с пятикратной расчетной длиной.
Относительное равномерное
удлинение δр определяют графически по диаграмме растяжения (рис. 2), записываемой соответствующим измерителем деформаций, установленным непосредственно на
образце.
Масштаб по оси деформаций
должен быть не менее 50:1.
Примечание. Определение δр производится на
участке диаграммы растяжения, заканчивающемся точкой В, которая соответствует
началу достижения максимальной нагрузки Рвр.
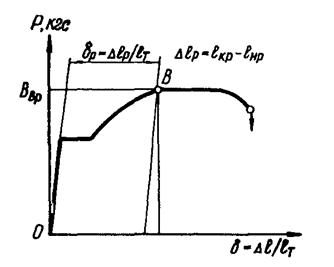
Рис. 2
4.2. Относительное
равномерное удлинение вычисляют с округлением до 0,5 %. При этом доли до 0,25 %
отбрасывают, а доли в 0,25 % и более принимают за 0,5 % (см. приложение).
4.3. Испытание считается
недействительным:
— при разрыве
образца по кернам (рискам), если при этом какая-либо
характеристика механических свойств по своей величине не отвечает установленным требованиям;
— при разрыве
образца в захватах испытательной машины или за пределами расчетной длины;
— при обнаружении ошибок в
проведении испытаний или записи результатов
испытаний.
В указанных случаях испытание
на растяжение должно быть повторено на отобранных от той же партии или плавки
новых образцах.
По первому методу (рис. 1)
Начальная расчетная длина lнр = 50
мм;
Конечная расчетная длина lкр = 58,4 мм,
![]()
По второму методу
Начальная площадь поперечного сечения
(10×30 мм) образца F0 = 300 мм2.
Конечная площадь поперечного
сечения образца (замеренная на расстоянии 4b0 от места разрыва) Fкр = 258 мм2
|
|
Источник






