Показатель деформационного упрочнения при растяжении
| 1. /as_ndis_0001.doc | Диссертация на соискание ученой степени кандидата технических наук Научный к т. н., доцент Хачатурьян С. В. Ташкент 2005 содержание |
3.3. Определение коэффициента деформационного упрочнения по
стандартным механическим характеристикам материалов и установление аналитической зависимости для оценки относительной
износостойкости
Для вычисления коэффициента деформационного упрочнения необходимо условную диаграмму растяжения σ = f(ε) (рис. 2.3) преобразовать в истинную S=f(e) (рис. 2.4.)

Рис. 2.3. Условная диаграмма растяжения
Кривые растяжения в координатах (рис. 2.3) напряжение — относительное удлинение (σ, ε) не представляют зависимости истинного сопротивления металла от величины деформации при растяжении. Подобные кривые на участке развития шейки образца приобретают даже прямо противоположную действительности особенность, показывая, например, падение условного напряжения при прогрессирующей, перед разрывом, пластической деформации, в то время как истинное напряжение растет [67].
Диаграмму напряжений при растяжении, можно рассматривать как характеризующую свойства данного материала при растяжении.
Эта характеристика механических свойств материала является, однако, условной. Если в начале испытания площадь поперечного сечения образца почти не изменяется, то, начиная с напряжений, равных пределу текучести, наступает заметное уменьшение этой площади, сначала равномерное по всей длине, а с момента перехода за предел прочности — местное. Таким образом, ординаты кривой на участке за пределом текучести представляют собой условные напряжения, отнесенные не к действительной площади сечения, а первоначальной.
Точно так же абсциссы диаграммы до достижения предела прочности зависят лишь от способности материала удлиняться; после же образования шейки величина относительного удлинения зависит и от соотношения размеров образца (длины и диаметра) и, таким образом, не является уже характеристикой только материала. Поэтому, чтобы получить график, более точно характеризующий свойства самого материала, строят так называемую диаграмму истинных напряжений. Она иллюстрирует связь между напряжениями и деформациями в том сечении образца, где происходит разрыв.
Для построения диаграммы истинных напряжений необходимо отмечать в разные моменты опыта величину силы, растягивающей образец, и одновременно измерять поперечные размеры образца в наиболее суженном месте.
Таким образом, если обозначить истинное напряжение S, а истинную площадь поперечного сечения в наиболее суженном месте F, то
S = Pi / Fi (2.19)
При больших деформациях начальная длина образца тоже значительно изменяется. В связи с этим истинное удлинение е должно быть отнесено к действительной длине стержня в данный момент испытания и может быть вычислено по формуле
e = (2.20)
где —первоначальная длина, а —длина в момент измерения. При больших значениях истинного удлинения оно обозначается е.
Установим зависимости между истинными и условными деформациями и истинными и условными напряжениями. При равномерной деформации по длине образца
e = = ln (2.21)
Окончательно
e = ln(1 + ε ), (2.22)
где ε = ∆l / условная относительная деформация.
Формула (2.21) при неравномерной деформации не может быть использована, так как затруднено измерение ∆l для вычисления ε .
При неравномерной деформации, с началом образования шейки, опыт показывает, что объем образца почти не меняется. Этот закон постоянства объема может быть записан так:
Fl = Fl (2.23)
где — первоначальная площадь поперечного сечения. Далее получим
Fl = (F- ∆F) (l + ∆l ) (2.24)
после деления на ;
1= (2.25)
или
(1 – ψ)(1 + ε) = 1 (2.26)
1 + ε = (2.27)
Отсюда, подставив последнее равенство в формулу (2.21), окончательно получим
e = ln (2.28)
Отметим, что величина ψ определяется по самому узкому месту шейки.
Для получения зависимости между истинными и условными напряжениями учтем, что
P = σF = SF (2.29)
где σ — условное напряжение, т. е. отнесенное к первоначальной площади поперечного сечения. Далее,
σ = S = S = S (1 – ψ) (2.30)
Таким образом, учитывая полученную ранее зависимость между ε и ψ, при равномерной деформации по длине образца
S = σ (1 –ε ) (2.31)
При неравномерной деформации, с началом образования шейки, истинное напряжение определяется непосредственно по формуле (2.19),так как нахождение условных напряжений в этой стадии работы образца бессмысленно из-за значительной разницы между F и F.
Диаграмма в координатах истинные напряжения — истинные деформации изображена на рис. 2.4.

Рис. 2.4. Истинная диаграмма напряжений.
Значение
Величина истинного предела прочности или истинного временного сопротивления S, определяется по формуле (2.31).
Значение истинного напряжения при разрыве определяется по формуле (2.19)
S= P/ F
Величина истинного равномерного удлинения находится по формуле (2.22), т. е.
e= ln (1 – ε )
где — есть условное относительное удлинение в момент начала образования шейки.
Наконец, значение полного истинного удлинения в момент разрыва определяется по формуле (2.28),
e=ln, (2.32)
где — вычисляется для места разрыва:
Как видно из диаграмм, представленных на рис.2.3 и 2.4, напряжение возрастает до самого разрыва, сначала быстро, после же достижения наибольшего значения нагрузки (напряжение S) менее резко. В момент разрыва напряжение, отнесенное к действительной площади сечения, оказывается большим предела прочности, вычисленного обычным способом.
Ординаты истинной диаграммы характеризуют способность материала сопротивляться пластической деформации.
Для продолжения пластической (остаточной) деформации нам приходится давать материалу все большее и большее напряжение; по мере роста пластической деформации материал оказывает ей все большее сопротивление. Это явление называется упрочнением. Способность материала к упрочнению характеризуется крутизной подъема’ истинной диаграммы, величиной tgα,
tg α == D, (2.33)
где D – коэффициент деформационного упрочнения.
В работе [68] на основании обширного экспериментального материала были установлены для вычисления SK следующие зависимости
SK=(1 + 1,35 ) при 0,15, (2.34)
SK=(0,8 + 2,06) при > 0,15 (2.35)
Возможное отклонение вычисленных по ним значений SK от экспериментально установленных в среднем составляет 6% [68].
Следовательно, относительная величина скрытой энергии, накопленной в материале рельса к моменту разрушения, легко может быть определена по стандартным механическим характеристикам рельсовой стали — пределу прочности,- пределу текучести, относительному сужению — .
То обстоятельство, что коэффициент деформационного упрочнения рассчитывается по стандартным механическим характеристикам металлов, позволило широко использовать в качестве экспериментального обоснования предложенного критерия данные, полученные другими исследователями.
Источник
[c.615]
Приведенные выше методы обработки кривых нагружения позволяют описать процесс деформационного упрочнения при помощи нескольких эмпирических параметров, в частности величины ад, коэффициента упрочнения /С1 (/Сг) и показателя деформационного упрочнения 1 (Яз), которые, однако, не указывают на физическую природу и конкретные механизмы такого упрочнения.
[c.135]
Hs — расстояние, на которое удалена траектория трещины от горизонтали на поверхности образца кр — коэффициент перегрузки внутренним давлением по отношению к рабочему циклическому давлению Ki — вязкость разрушения металла K s вязкость разрушения в коррозионной среде К[р — коэффициент интенсивности напряжения образца с разным радиусом в вершине концентратора напряжений Kj — коэффициент концентрации напряжений Шр — показатель степени в уравнении Париса п — показатель деформационного упрочнения материала Пс — количество скачков дискретного подрастания трещины N — число циклов
[c.23]
Коэффициент пропорциональности в формуле (5.31) зависит от показателя деформационного упрочнения и лежит в диапазоне 0,38-1,00 [83]. Более того, деформация материала происходит неоднородно вдоль всего фронта страгиваемой трещины, достигая минимальной величины в его срединной части [84]. Столь широкий диа-
[c.244]
Отсюда следует, что если при деформации металла пластичность высока, а упрочнение (показатель степени в экспоненте) невелико, то локальный механохимический эффект в основном зависит от величины пластической деформации и примерно пропорционален той ее части, которая связана с новыми дислокациями (в пределах стадии II деформационного упрочнения).
[c.58]
Значение остаточных напряжений, глубина и степень деформационного упрочнения, а также получаемая шероховатость поверхностного слоя зависят от материала обрабатываемой детали, выбранного метода упрочнения и его технологических п раметров. Технологические показатели основных методов упрочняющей обработки поверхностей деталей машин приведены в табл. 7.11—7.14.
[c.172]
Нанесение на чертежах обозначений покрытий. Правила нанесения на чертежах изделий всех отраслей промышленности обозначений покрытий (защитных, декоративных, электроизоляционных, износоустойчивых и т. п.), а такл е показателей свойств материалов, получаемых в результате термической и других видов обработки [химико-термической, деформационного упрочнения (наклепа) и т. п.) установлены стандартом [160].
[c.376]
Показатель деформационного упрочнения определяет форму кривой деформации и является структурно-чувствительной характеристикой материала. Его значение определяется из (3.1)
[c.57]
Другими словами, в точке неустойчивости нагрузки величина истинной деформации равна показателю деформационного упрочнения. Многие из введенных в этом разделе понятий будут использованы в дальнейшем.
[c.111]
Таким образом, точка неустойчивости достигается, когда истинная кольцевая деформация 6i становится равной по величине половине показателя деформационного упрочнения материала. Для определения давления при котором достигается точка неустойчивости, подставляем (5.109) в (5.107) и получаем
[c.125]
Значения коэффициента k и показателя деформационного упрочнения п для стали SAE 4130 можно найти в таблице к рис. 5.2 k= = 154 500 фунт/дюйм и =0,156. Начальная толщина о=0,125 дюйма и начальный диаметр Do=18 дюймов были заданы ранее. Подставляя эти числовые данные в (5.110), получаем
[c.125]
Вычертите кривую зависимости между напряжениями и деформациями в логарифмических координатах и определите коэффициент прочности k и показатель деформационного упрочнения п.
[c.128]
Предел текучести о =00,,, где To,i—напряжение при относительной деформации, равной 0,2% п —показатель деформационного упрочнения BHN —число твердости по Бринелю
[c.277]
Величины О/ и могут быть аппроксимированы способом, описанным в разд. 8.5. Используя энергетические соображения, постоянные Ь к с можно выразить через показатель деформационного упрочнения при циклическом деформировании п (см. рис. 8.17) с помощью соотношений [16]
[c.384]
| Рис. 2.1. Зависимость показателя деформационного упрочнения т от запаса пластичности исследованных сталей (обозначения по табл. 2.1). | 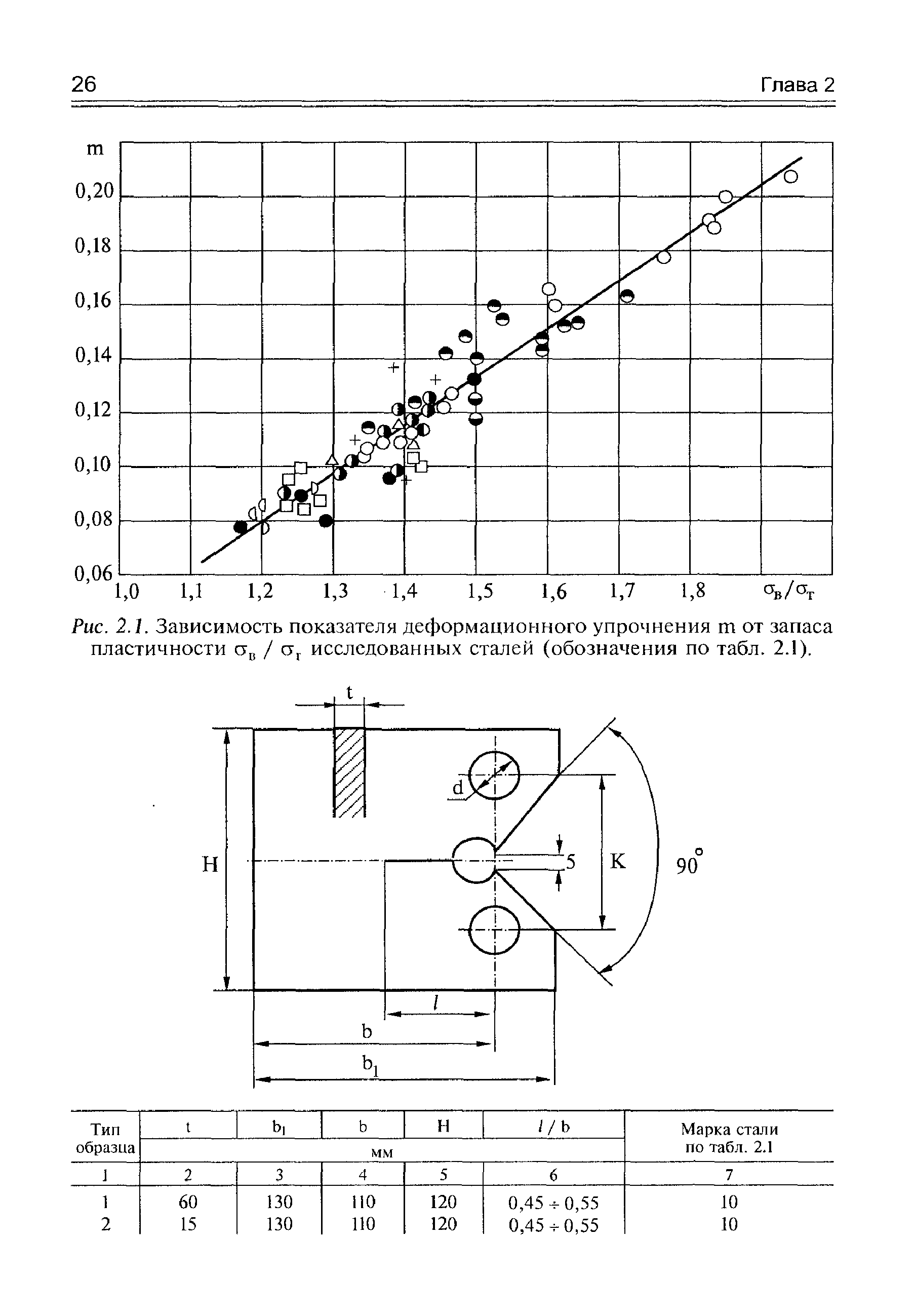 |
Уравнение прямой (2.5) (уравнение линии затупления трещины ) получено из предположения [22], что в момент страгивания трещины увеличение ее размера равно размеру зоны вытяжки и составляет половину критического раскрытия трещины Л/ = 5(./2. С другой стороны, величина З-интеграла связана с раскрытием трещины соотношением 3 = а б. Учет деформационного упрочнения путем замены предела текучести о. на величину о приводит к уравнению (2.5). Однако, согласно исследованиям [42, 50, 51 и др.], связь между критическими значениями 1-интеграла и раскрытием трещины 5(, для сталей с невысокими показателями упрочнения имеет вид
[c.38]
Для исследованных сталей а == 0,25 р = 2,32. В соответствии с уравнениями (2.24) показатель р зависит от уровня разрушающего напряжения и показателя деформационного упрочнения. Данная зависимость представлена на рис. 2.25, при этом, несмотря на значительный разброс данных, средние значения р при / а . [c.56]
Основные характеристики механических свойств (условный предел текучести сто 2, предел прочности а д, относительное удлинение 5 и сужение ), показатель деформационного упрочнения т, прочность межслойной связи на отрыв сгр и срез Тр) приведены в табл. 5.1 и на рис. 5.1, 5.2. Зональное распределение интегральных механических характеристик в биметаллах определялось путем вырезки плоских образцов сечением 2 х 10 мм (см. рис. 5.1) и 2 х 3 мм (см. рис. 5.2) из соответствующих зон композиции.
[c.110]
Основные характеристики механических свойств (а — предел текучести, Оод — условный предел текучести, — временное сопротивление, 8 — сопротивление разрыву, )/, 5 — относительное сужение и удлинение соответственно, Е — модуль упругости и т — показатель деформационного упрочнения), определенные на укороченных образцах с диаметром рабочей части 6…10 мм указанных сплавов, приведены в табл. 7.1. Пределы текучести сплавов были в диапазоне от 9,4 до 41,4 кгс/мм , пределы прочности — от 20,5 до 49,0 кгс/мм , при этом отношение предела текучести к пределу прочности составляло о,46…о,94. На рис. 7.2 показаны начальные участки диаграмм статического растяжения в истинных координатах (а — е) для сплавов
[c.181]
Показатель деформационного упрочнения 165, 170 Поле
[c.348]
Мы постулируем, что температурная зависимость /С,,, имеет вышеприведенный вид, поэтому пластическая зона при каждой температуре должна иметь такой размер, при котором локальные растягивающие напряжения были бы равны разрушающему напряжению скола, как и в образцах с надрезом. Только недавно с развитием метода конечных элементов, позволяющего определить распределение упруго-пластических напряжений перед вершиной трещины, стала возможной количественная проверка этой гипотезы. Типичное распределение напряжений для материала, не испытывающего деформационного упрочнения, и материалов с различным показателем деформационного упрочнения при Оу/ = = 0,0025 (среднее значение в изученном интервале температур) представлено на рис. 42 [26].
[c.213]
Поверхностная энергия, рассчитанпая по раскрытию верш ны трещины Удельная энергия разрушения Размер пластической зоны в вершине трещины Коэффициент деформации пластически деформированной зош у вершины трещины Расстояние, измеренное от вершины трещины, где возника разрушение Амплитуда циклической деформации Амплитуда циклической пластической деформации Показатель деформационного упрочнения Показатель деформационного упрочнения при циклических нагружениях
[c.324]
Ройер Р, Влияние показателя деформационного упрочнения и концентрации напряжений на характер разрыва сосудов давления // Теоретические основы инженерных расчетов Тр. амер. об-ва инженеров-механиков — Т.96
[c.265]
С точки зрения механики разрушения чувствительность материала к скорости нагружения оценивалась Краффтом и Ирвиным [65, 242]. Ими получено простое соотношение (выполняющееся на некотором расстоянии перед краем трещины) между Ki при испытании с возрастающей нагрузкой, показателем деформационного упрочнения материала п (в степенном законе диаграммы деформации) и скоростью деформации е
[c.307]
Из других методик обработки кривых нагружения можно отметить подход Рамани и Родригеса [321], которые для нахождения показателя деформационного упрочнения щ определяют работу Лх, затраченную на деформирование образца в некотором интервале деформаций г — Вх). Интегрируя уравнение (3.24), можно показать, что величина
[c.134]
Противоречивость приведенных данных частично можно объяснить чисто методическими упущениями, связанными, например, с определением параметров деформационного упрочнения из условных диаграмм нагрузка —деформация, недопустимость чего отмечается в работе [351]. Кроме того, под коэффициентом деформационного упрочнения часто понимают скорость деформационного упрочнения й 1с1е, которая является постоянной величиной только при наличии стадии линейного упрочнения, а при переходе к параболическому упрочнению эта величина определяет скорость упрочнения при определенной степени деформации, т. е. только в одной точке кривой нагружения. Неучет последнего при анализе величины й81йе может привести к искажению результатов эксперимента. С другой стороны, изучаются разные параметры упрочнения [331, 351, 352] — показатель деформационного упрочнения п, коэффициент параболического упрочнения К, скорость упрочнения й31йе, сопоставление которых также может приводить к противоречивым результатам. Часто сравниваются интенсивности упрочнения различных металлов и сплавов исходя только из сравнения их диаграмм нагружения [252, 350].
[c.151]
Ef — предельная деформация при разрзтпении монотонно растягиваемого образца п — показатель деформационного упрочнения материала.
[c.236]
Показатель деформационного упрочнения п, определяющий интенсивность протекания процесса пластической деформации материала, рассчитывают в соответствии с уравнением Коф-фина-Мэнсона (5.37). Он является основной константой, от которой зависит скорость роста усталостных трещин в области малоцикловой усталости при фиксированном уровне размаха пластических деформаций Ле ,/. Испытания, например, сплава 800Н при 700 °С со скоростью деформации 4-10 с показали, что соотношение (5.35) достаточно точно позволяет оценить распространение усталостных трещин [112]. В результате обобщения экспериментальных данных по различным маркам нержавеющих сталей (8 марок) и жаропрочным сплавам (6 марок) установлено, что показатель степени при размахе пластической деформации изменяется в интервале 1-2 [110].
[c.246]
В этом эмпирическом соотношении кип — постоянные материала. Постоянная k называется коэффициентом прочности, а постоянная п — показателем деформационного упрочнения. На рис. 5.2 приведены графики зависимости истинного напряжения от истинной деформации в логарифмических координатах для некоторых используемых в машиностроении сплавов. Там же приведена таблица значений /г и п для этих сплавов. Однако соотношение (5.18) описывает поведение не всех материалов, поэтому для описания поведения некоторых других материалов предложен ряд других эмпири-
[c.108]
Одной из наиболее информативных характеристик трещино-стойкости нелинейной механики разрушения является коэффициент интенсивности деформаций в упругопластической области К1е [1, 65-67], применимый в условиях статического и циклического нагружения. Его использование в инженерных расчетах [1, 68-71] позволяет определять запасы прочности и долговечности по предельным нагрузкам, локальным упругоплаетическим деформациям, размерам трещин и числам циклов нагружения. При этом основа расчетов — традиционные характеристики механических свойств (пределы текучести и прочности, относительные удлинение и поперечное сужение, показатель деформационного упрочнения и др.). Учитывается также влияние уровня номинальных напряжений, изменение параметров деформационного упрочнения, степени объемности напряженного состояния и предельной пластичности материала.
[c.53]
| Рис. 6.3, Соотношение между показателем (а) или коэффициентом (б) деформационного упрочнения и диаметром субзерен при однонаправленной II циклической деформации [4, 5] | ![Рис. 6.3, Соотношение между показателем (а) или коэффициентом (б) <a href="/info/38182">деформационного упрочнения</a> и диаметром субзерен при однонаправленной II циклической деформации [4, 5]](https://mash-xxl.info/pic1/087149151028003049012188056057181085009025148247.png) |
На рис. 6.3 приведены зависимости показателя деформационного упрочнения п и коэффициента деформационного упрочнения k нержавеющих сталей 304 и 316 при однонаправленном растяжении и циклической деформации при высокой температуре от диаметра субзерен d, определенного с помощью просвечивающего электронного микроскопа. Видно, что зависимости параметров деформации, характеризующих соотношение напряжение—деформация ст = kг , от диаметра субзерен одинаковы. Выведенное по экспериментальным данным соотношение имеет вид
[c.197]
Предложенная модель разрушения конструкционных сплавов с трещиной при циклическом нагружении учитывает влияние на вязкость разрушения изменения характеристик механических свойств материалов в пластически деформируемой зоне у вершины трещины при циклическом нагружении и класса материала (циклически разу-прочняющийся, упрочняющийся, стабильный). Для количественной оценки вязкости разрушзния необходимо знать закономерности изменения параметров диаграмм циклического деформирования (ширины петли пластического гистерезиса), циклического предела пропорциональности, циклического предела текучести, показателя деформационного упрочнения (в зависимости от режимов нагружения, класса материала и условий испытаний, например температуры), которые определяются при циклическом нагружении гладких образцов.
[c.221]
Часто криэую истинных напряжений а х = степенной зависимостью Стд. = Се», где п — показатель деформационного упрочнения. Подставляя это выражение (VI.27), получим, что шейка на образце появляется при относительном удлинении
[c.165]
Результаты испытаний на растяжение дают возможность установить анизотропию механических свойств исследуемого металла в плоскости листа и по его толш ине. Большие значения отношения равномерных деформаций по ширине к равномерным деформациям по толщине образцов, вьфезанных из листа вдоль и поперек прокатки, свидетельствуют о большей склонности металла к деформации в плоскости листа, а меньшие — к деформациям по толщине, что приводит к утонению и разрыву металла. Методика определения коэффициента пластической анизотропии, показателя деформационного упрочнения и неравномерности пластической деформации по результатам
[c.254]
Повреждение материалов в конструкциях
(1984) — [
c.0
]
Источник
