По графикам зависимости силы упругости возникающей при растяжении
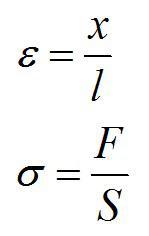
Можно не знать закон Ома и сидеть дома. Но если не знаешь закон Гука – лучше тоже не выходить. Особенно, если идешь на экзамен по физике.
Здесь устраняем пробелы в знаниях и разбираемся, как решать задачи на силу упругости и применение закона Гука. А за полезной рассылкой для студентов добро пожаловать на наш телеграм-канал.
Сила упругости и закон Гука: определения
Сила упругости – сила, препятствующая деформациям и стремящаяся восстановить первоначальные форму и размеры тела.
Примеры действия силы упругости:
- пружины сжимаются и разжимаются в матрасе;
- мокрое белье колышется на натянутой веревке;
- лучник натягивает тетиву, чтобы выпустить стрелу.
Простейшие деформации – деформации растяжения и сжатия.
Закон Гука:
Деформация, возникающая в упругом теле под действием внешней силы, пропорциональна величине этой силы.
Коэффициент k – жесткость материала.
Есть и другая формулировка закона Гука. Введем понятие относительной деформации «эпсилон» и напряжения материала «сигма»:
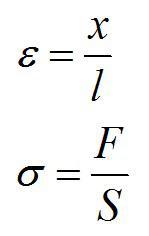
S – площадь поперечного сечения деформируемого тела. Тогда закон Гука запишется так: относительная деформация пропорциональна напряжению.
Здесь Е – модуль Юнга, зависящий от свойств материала.
Закон Гука был экспериментально открыт в 1660 году англичанином Робертом Гуком.
Вопросы на силу упругости и закон Гука
Вопрос 1. Какие бывают деформации?
Ответ. Помимо простейших деформаций растяжения и сжатия, бывают сложные деформации кручения и изгиба. Также разделяют обратимые и необратимые деформации.
Вопрос 2. В каких случаях закон Гука справедлив для упругих стержней?
Ответ. Для упругих стержней (в отличие от эластичных тел) закон Гука можно применять при малых деформациях, когда величина эпсилон не превышает 1%. При больших деформациях возникают явления текучести и необратимого разрушения материала.
Вопрос 3. Как направлена сила упругости?
Ответ. Сила упругости направлена в сторону, противоположную направлению перемещения частиц тела при деформации.
Вопрос 4. Какую природу имеет сила упругости?
Ответ. Сила упругости, как и сила трения – электромагнитная сила. Она возникает вследствие взаимодействия между частицами деформируемого тела.
Вопрос 5. От чего зависит коэффициент жесткости k? Модуль Юнга E?
Ответ. Коэффициент жесткости зависит от материала тела, а также его формы и размеров. Модуль Юнга зависит только от свойств материала тела.
Задачи на силу упругости и закон Гука с решениями
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Задача №1. Расчет силы упругости
Условие
Один конец проволоки жестко закреплен. С какой силой нужно тянуть за второй конец, чтобы растянуть проволоку на 5 мм? Жесткость проволоки известна и равна 2*10^6 Н/м2.
Решение
Запишем закон Гука:
По третьему закону Ньютона:
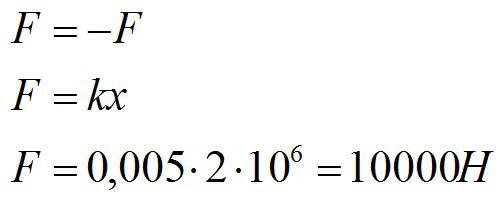
Ответ: 10 кН.
Задача №2. Нахождение жесткости пружины
Условие
Пружину, жесткость которой 100 Н/м, разрезали на две части. Чему равна жесткость каждой пружины?
Решение
По определению, жесткость обратно-пропорциональна длине. При одинаковой силе F неразрезанная пружина растянется на х, а разрезанная – на x1=x/2.
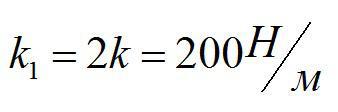
Ответ: 200 Н/м
При растяжении пружины в ее витках возникают сложные деформации кручения и изгиба, однако мы не учитываем их при решении задач.
Задача №3. Нахождение ускорения тела
Условие
Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины, которая при движении растянулась на 2 см. Жесткость пружины 200 Н/м. Определить ускорение, с которым движется тело.
Решение
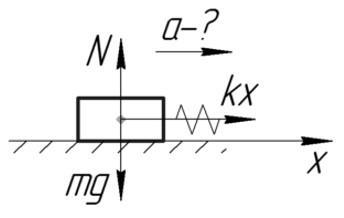
За силу, которая приложена к телу и заставляет его двигаться, можно принять силу упругости. По второму закону Ньютона и по закону Гука:
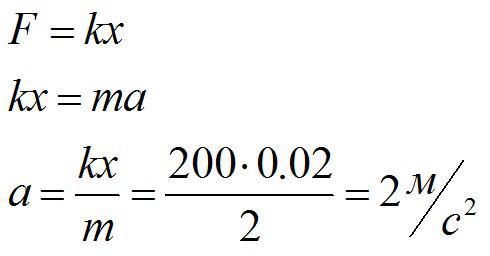
Ответ: 2 м/с^2.
Задача №4. Нахождение жесткости пружины по графику
Условие
На графике изображена зависимость модуля силы упругости от удлинения пружины. Найти жесткость пружины.
Решение
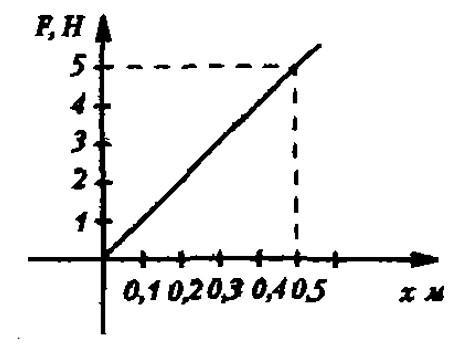
Вспоминаем, что жесткость равна отношению силы и удлинения. Представленная зависимость – линейная. В любой точке прямой отношение ординаты F и абсциссы х дает результат 10 Н/м.
Ответ: k=10 Н/м.
Задача №5. Определение энергии деформации
Условие
Для сжатия пружины на х1=2 см надо приложить силу 10 Н. Определить энергию упругой деформации пружины при сжатии на х2=4 см из недеформированного состояния.
Решение
Энергия сжатой пружины равна:
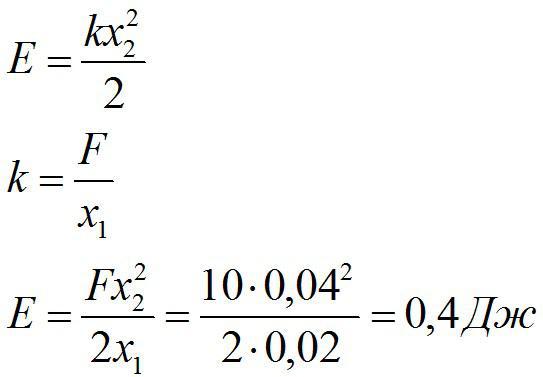
Ответ: 0,4 Дж.
Нужна помощь в решении задач? Обращайтесь за ней в профессиональный студенческий сервис.
Автор
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Источник
Сила – это количественная мера взаимодействия тел. В рамках классической механики мы имеем дело со следующими видами сил: силами инерции, гравитационными, электростатическими, упругими, силами трения и сопротивления. Объектами воздействия классических сил являются м.т., с.м.т., твердое тело, сплошная среда (твердое вещество, газ, жидкость).
Силы упругости, силы трения и сопротивления определяются взаимодействиеями между молекулами вещества и имеют в своей основе электромагнитное происхождение и действуют в масштабах межмолекулярных расстояний.
Закон Гука
Закон Гука применим к деформируемым объектам, возвращающимся к исходному состоянию после снятия силы. Например, для растягивающейся пружины справедлива формула силы
F = kx, (1)
где F – действующая сила,
k – коэффициент пропорциональности, или жесткость пружины,
x – растяжение пружины.
Кроме линейных объектов типа пружины, на практике встречается множество других типов деформируемых объектов, по отношению к которым можно применять закон Гука. Только в этом случае коэффициент k может быть тензором 2–го порядка соответствующей размерности. Движение при этом обратимо.
Деформацией называют изменение формы, размеров или объема тела. Деформация может быть вызвана действием на тело приложенных к нему внешних сил. Если после прекращения действия сил тело возвращается в прежнее состояние (деформация исчезает), то деформация называется упругой. Деформации, сохраняющиеся и после того, как внешние силы перестали действовать на тело – пластическими. Обычно деформация бывает упругой, если ее величина не превосходит определенного предела (предела упругости). Внутри такого деформированного тела возникают силы, называемые силами упругости.
Различают деформации растяжения или сжатия (одностороннего или всестороннего), изгиба, кручения и сдвига.
Силы упругости действуют в любом сечении деформированного тела, а также в месте его контакта с телом, вызывающим деформации. В случае одностороннего растяжения или сжатия сила упругости направлена вдоль прямой, по которой действует внешняя сила, вызывающая деформацию тела, противоположно направлению этой силы и перпендикулярно поверхности тела.
Природа упругих сил электрическая. При деформациях твердого тела его частицы (атомы, молекулы, ионы), находящиеся в узлах кристаллической решетки, смещаются из своих положений равновесия. Этому смещению противодействуют силы взаимодействия между частицами твердого тела, удерживающие эти частицы на определенном расстоянии друг от друга. Поэтому при любом виде упругой деформации в теле возникают внутренние силы, препятствующие его деформации. Связь между силой упругости и упругой деформацией тела (при малых деформациях) была экспериментально установлена английским физиком Гуком.
Закон Гука для одностороннего растяжения (сжатия) формулируют так: сила упругости, возникающая при деформации тела, пропорциональна удлинению этого тела. Опытным путем установлено, что при малых деформациях упругая сила пропорциональна величине деформации. Например, при растяжении пружины на величину Δlупругая сила F вдоль оси пружины будет равна
F = –kΔl, (2)
где F – сила упругости;
Δl – удлинение (деформация) тела;
k – коэффициент пропорциональности, зависящий от размеров и материала тела, называемый жесткостью. Единица жесткости в СИ – ньютон на метр (Н/м).
Знак «–» в формуле (2) указывает, что направление силы противоположно направлению деформации (при растяжении пружины сила F сжимает ее и наоборот, при сжатии растягивает).
Упругую силу принято характеризовать не ее непосредственной величиной F, а отношением F к площади поверхности S, через которую она действует. Это отношение называют напряжением. В случае, когда сила F перпендикулярна поверхности S, напряжение называют нормальным. Его обозначают σ. Напряжение измеряют в паскалях [Па]. (1 Па = 1 Н / 1 м2).
Деформацию твердых тел чаще характеризуют не абсолютным изменением длины Δl, а относительным удлинением ε (3)
где l – длина тела. ε – безразмерная величина.
При малых деформациях относительное удлинение пропорционально нормальному напряжению. Эту связь деформации и напряжения также называют законом Гука. Его принято записывать в следующей форме (4):
Коэффициент пропорциональности Е в законе Гука характеризует упругость данного материала и называется модулем (продольной) упругости (модулем Юнга). Модуль Юнга численно равен такому нормальному напряжению, которое должно было бы возникнуть в теле при увеличении его длины в 2 раза (если бы для такой большой деформации выполнялся закон Гука). Модуль упругости выражается в паскалях.
Диаграмма растяжения
Используя формулу (3), (4), по экспериментальным значениям относительного удлинения ε можно вычислить соответствующие им значения нормального напряжения σ, возникающего в деформированном теле, и построить график зависимости σ от ε. Этот график называют диаграммой растяжения. Подобный график для металлического образца изображен на рис. 1.
Рис. 1. График деформации реального тела.
На участке 0–1 график имеет вид прямой, проходящей через начало координат. Это значит, что до определенного значения напряжения σп деформация является упругой и выполняется закон Гука, т. е. нормальное напряжение пропорционально относительному удлинению. Максимальное значение нормального напряжения σп, при котором еще выполняется закон Гука, называют пределом пропорциональности.
При дальнейшем увеличении нагрузки зависимость напряжения от относительного удлинения становится нелинейной (участок 1–2), хотя упругие свойства тела еще сохраняются. Максимальное значение нормального напряжения, при котором еще не возникает остаточная деформация, называют пределом упругости. (Предел упругости лишь на сотые доли процента превышает предел пропорциональности.) Увеличение нагрузки выше предела упругости (участок 2–3) приводит к тому, что деформация становится остаточной.
Затем образец начинает удлиняться практически при постоянном напряжении (участок 3–4 графика). Это явление называют текучестью материала. Нормальное напряжение σт, при котором остаточная деформация достигает заданного значения, называют пределом текучести.
При напряжениях, превышающих предел текучести, упругие свойства тела в известной мере восстанавливаются, и оно вновь начинает сопротивляться деформации (участок 4–5 графика). Максимальное значение нормального напряжения σпр, при превышении которого происходит разрыв образца, называют пределом прочности.
Таблица 1. Пример таблицы модулей упругости металлов
—————————————————————————————-
Ссылка на мою статью Как написать формулы в статье на Дзен?
Мои странички на Дзен: https://zen.yandex.ru/id/5e036c95fc69ab00aecfe6e9
Если хотите узнать, что обозначает слово или словосочетание, в ОПЕРЕ выделите это слово(сочетание), нажмите правую клавишу мыши и выберите «Искать в …», далее — «Yandex». Если это текстовая ссылка – выделите ее, нажмите правую клавишу мыши, выберите «перейти …». Все! О-ля-ля!
Если вам понравилась статья, то поставьте «лайк» и подпишитесь на канал! Если не понравилась – все равно комментируйте и подписывайтесь. Этим вы поможете каналу. И делитесь ссылками в ваших соцсетях!
Источник
Цели урока:
1. Обучающая: ввести понятие «сила
упругости», выяснить зависимость силы
упругости от деформации, опытным путем
установить закон Гука, вывести формулу,
выражающую закон Гука.
2. Развивающая: развить умственные и
творческие способности учащихся, познавательный
интерес к предмету, формировать умение объяснять
окружающие явления, происходящие в природе.
3. Воспитательная: способствовать
формированию сознательного творческого
отношения к обучению, умение работать в
коллективе и понимать значение полученных
знаний.
Ход урока
I. Организационный момент (1 минута)
а) приветствие;
б) подготовка аудитории к работе.
II. Актуализация опорных знаний.
а) фронтальный опрос;
б) индивидуальная работа ученика у доски (на
доске дать характеристику силы тяжести по плану
учителя);
в) решить задачу (расчет силы тяжести).
III. Изложение нового материала.
IV. Закрепление нового материала (решение
задач).
V. Подведение итогов.
VI. Рефлексия.
I. Организационный момент (1 минута)
Здравствуйте, ребята! Сегодня у нас урок
открытых дверей, и, поэтому, мы должны особенно
постараться. Покажите все свои знания и умения, и
будьте активны, не бойтесь ошибаться, не
ошибается только тот, кто ничего не делает.
II. Актуализация опорных знаний.
Учитель: Повторим пройденный материал.
1) у доски подготовить характеристику силы
тяжести по плану.
План изучения физической величины:
- Определение силы тяжести;
- Вектор или скаляр;
- Буквенное обозначение силы тяжести;
- Формула силы тяжести;
- Единицы измерения величины силы;
- Направление и точка приложения силы тяжести,
показать на чертеже.
2) Решить задачу:
Вычислить силу тяжести, действующую на тело
массой 2 кг. Изобразить эту силу графически на
чертеже в масштабе 10 Н / 1 см.
Проверка индивидуальной работы у доски
консультантами и выставление оценок.
3) Фронтальный опрос (слайд 1).
1. В результате чего может меняться скорость
тела?
Ответ: в результате взаимодействия с другим
телом.
2. Что такое сила? Каковы единицы силы?
Ответ: Сила — это мера взаимодействия тел,
измеряют силу в ньютонах, килоньютонах,
меганьютонах.
3. Что может произойти с телом, на которое
действует сила?
Ответ: измениться скорость тела или
деформируется.
4. От чего зависит результат действия силы на
тело?
Ответ: от модуля силы, от направления силы, от
точки приложения силы.
5. Что является причиной падения всех тел на
землю?
Ответ: притяжение земли, т.е. сила тяжести.
6. Какую силу называют силу тяжести?
Ответ: сила, с которой земля притягивает к себе
тела.
7. В чем причина ее возникновения?
Ответ: гравитационное поле земли.
8. Почему сила тяжести на полюсах земли
несколько больше, чем на экваторе и других
широтах?
Ответ: земной шар немного сплюснут у полюсов,
поэтому тела, находящиеся около полюсов,
расположены немного ближе к центру земли,
поэтому сила тяжести на полюсе немного больше,
чем на экваторе или на других широтах.
9. Как зависит сила тяжести от массы тела?
Ответ: сила тяжести прямо пропорциональна
массе этого тела, т.е. чем больше масса, тем больше
сила тяжести действует на это тело.
10. Как направлена сила тяжести?
Ответ: она всегда направлена вертикально вниз.
11. На какой из автомобилей — легковой или
грузовой действует большая сила тяжести? Почему?
Ответ: больше сила тяжести действует на
грузовой автомобиль, т.к. у него больше масса, а
чем больше масса, тем больше сила тяжести.
12. Объем бензина в баке автомашины уменьшили в 2
раза. Как при этом измениться сила тяжести
бензина?
Ответ: объем прямо пропорционален массе, сила
тяжести уменьшается.
III. Изложение нового материала.
Проблемная ситуация (роняю мяч из рук).
Учитель: Вы знаете, что все тела на
поверхности Земли испытывают ее притяжение (в
этот момент роняю мяч из рук). На любое тело,
находящееся на поверхности Земли или вблизи ее
действует сила тяжести.
Снежинка, падающая с тела, движется к Земле. Но
упав на крышу, она прекращает свое движение.
Значит, что-то мешает снежинке двигаться вниз.
? Что же мешает снежинке и всей толще снега,
находящейся на крыше, двигается к центру Земли
под действием силы тяжести?
Ответ: снегу мешает продолжать двигаться сила,
действующая на него со стороны крыши. Эта сила
направлена в сторону, противоположную
направлению силы тяжести и численно равна ей. Она
компенсирует силу тяжести, и снег ведет себя так,
как если бы на него не действовало никакое тело,
т.е. находится в состоянии покоя.
Учитель: Рассмотрим еще один пример
компенсации силы тяжести.
Опыт 1 (с деревянной линейкой и гирей).
Учитель: Горизонтально расположенная
линейка на опорах. Если поставить гирю на эту
линейку, то она начнет прогибаться по мере
движения гири вниз. Линейка деформировалась и
при определенной величине деформации, линейка и
гиря останавливаются, гиря движется вниз до тех
пор, пока сила на гирю со стороны линейки не
уравновесит силу тяжести.
Что это за сила?
А чтобы узнать, как называется эта сила, вы
закончите фразу из стихотворения, которое я вам
прочитаю (слайд 2).
Вот дощечка через речку,
По ней как речку перейти?
Шагом или бегом без трудностей,
Поможет нам сила (упругости).
Учитель: Сформулируйте тему урока (слайд 3)
Поставьте перед собой цель урока.
Учитель: Запишем тему урока «Сила
упругости. Закон Гука» (слайд 3).
Вернемся к нашему опыту и изобразим его на
чертеже.
Вывод: деформированная линейка действует
на гирю силой, которая уравновешивает силу
тяжести, действующую на гирю.
Учитель: Сформулируем определение силы
упругости: сила, возникающая при деформации тела,
называется силой упругости (сла йд 4).
Разновидности деформации (виды деформации)
Опыт 2 (с резиновым ластиком).
Учитель: Подвергните ластик деформации, т.е.
согните, растяните, закрутите, сожмите.
Деформации различают по характеру изменения
формы и размера тела (слайд 5). Это изгиб,
растяжение, сжатие, кручение — это виды
деформации. Проведем опыт с двумя шариками.
Опыт 3 (пластилиновый и резиновый шарики).
1) Сомните резиновый шарик
— Что произошло с резиновым шариком?
(ответ: он деформировался);
— Что происходит с резиновым шариком после
прекращения внешнего воздействия?
(ответ: он восстановил свои прежние формы и
размер)
2) Сожмите пластилиновый шарик
— Что произошло с пластилиновым шариком?
(ответ: он деформировался)
— Что произошло пластилиновым шариком после
прекращения внешнего воздействия?
(ответ: он не восстановил свою формулу и
размеры).
Вывод: деформация делится на два типа — упругую
и пластическую (слайд 6)
Комментирую слайд 6.
Учитель:
1. После упругой деформации тело полностью
восстанавливает свою первоначальную форму и
размеры.
2. После пластической деформации тело полностью
сохраняет вновь приобретенную форму и размеры.
Так происходит при лепке из глины или
пластилина. Пластическая деформация
используется в технике в таких процессах, как
ковка и штамповка.
Физкультминутка (слайд 8)
Учащимся предлагается встать со своих мест, и,
закрепляя виды деформации, показать с помощью
своего тела все 5 видов деформации: растяжение,
сжатие, сдвиг, кручение, изгиб.
Учитель: Молодцы! Во время физкультминутки вы
испытали на себе различные виды деформации.
Причины возникновения силы упругости.
Учитель: А теперь давайте выясним, почему
возникает сила упругости?
? Что вы знаете о внутреннем строении
твердых тел?
Ответ: все тела состоят из молекул, между
которыми есть промежутки. В твердых телах
молекулы образуют кристаллическую решетку, а,
следовательно, между молекулами существую
определенные расстояния.
Учитель: При деформации тела изменяются
промежутки между молекулами, которые приводят к
возникновению межмолекулярных сил притяжения
(при растяжении) и отталкивания (при сжатии).
Давайте сформулируем вывод (слайд 9).
Вывод: причиной силы упругости являются
межмолекулярные силы взаимодействия.
Закон Гука.
Учитель: Деформация тела чаще всего очень
мала и незаметна визуально. Например, когда гиря
стоит на столе, деформация стола не видна, но
именно она является причиной того, что тело
неподвижно, хотя на него действует сила тяжести.
Гораздо проще исследовать силу упругости, когда
деформация хорошо заметна и легко поддается
измерению. Так, например, происходит при
растяжении пружины, если к ней подвешивать
поочередно один, два, три груза, то можно
заметить, что деформация пружины увеличивается,
а, следовательно, увеличивается и сила упругости.
Работа в парах.
Учитель: Определите опытным путем, как
зависит сила упругости от величины деформации.
Опыт 4 (с пружиной и грузами по 1Н, 2Н, 3Н)
Карточка-инструкция на каждую парту.
? Как зависит сила упругости от удлинения
пружины?
Инструкция эксперимента
1) Подвесить к пружине одну гирю (1Н) и измерить
удлинение пружины.
2) Подвесить к пружине 2 гири (2Н) и снова измерить
удлинение пружины.
3) Подвесить к пружине 3 гири (3Н) и измерить
удлинение пружины.
4) Результаты измерений занести в таблицу:
| № опыта | Сила упругости (Fупр) | Удлинение пружины (? l) в см |
| 1 | 1 Н | 2,5 см. |
| 2 | 2 Н | 5 см. |
| 3 | 3 Н | 7,5 см. |
5) построить график зависимости силы упругости
от удлинения пружины.
6) Что является графиком зависимости силы
упругости от удлинения пружины?
7) Сделайте вывод: как зависит сила упругости от
удлинения пружины?
Ответ: сила упругости прямо пропорциональна
удлинению пружины (т.е. прямая зависимость).
Вывод: эта зависимость была обнаружена на опыте
английским физиком Робертом Гуком (1635-1703) и носит
название Закон Гука (слайд 10).
Закон Гука: модуль силы упругости при
растягивании (или сжатии) тела прямо
пропорционален изменению длины тела.
Чем больше удлинение тела, тем больше сила
упругости.
Опыт 5. (2 пружины одинаковой формы и размера)
Учитель: Рассмотрим две пружины одинаковой
длины. Если к ним подвесить два груза одинаковой
массы, то они растянутся неодинаково.
? Почему пружины растягиваются
неодинаково?
При расчете силы упругости надо учитывать не
только удлинение деформированного тела, но и сам
деформируемый предмет, его размеры, форму и
материал, из которого он изготовлен, эти понятия
входят в коэффициент упругости тела (или
коэффициент жесткости тела).
K = [H / M]
Вывод опыта 5: это означает, что коэффициент
упругости у пружин разный, если правая пружина
удлинялась больше левой, то ее коэффициент
жесткости меньше (слайд 11).
IV. Закрепление.
Вывод: мы выяснили, что при внешнем воздействии
на тело в нем на межмолекулярном уровне
возникают изменения:
1) деформация приводит к изменению расстояния
между молекулами;
2) существуют различные виды деформации;
3) сила, которая возникла при деформации,
называется силой упругости;
4) при малых деформациях растяжения (сжатия)
сила упругости прямо пропорциональна удлинению
тела.
V. Подведение итогов. Домашнее задание: параграф
25, упр. 9 (1).
Сегодня вы были очень активны. Спасибо вам,
ребята! Думаю, что знания, полученные на уроке,
пригодятся вам в дальнейшем.
Оцените свою работу на уроке (Карточка успеха).
| Виды деятельности | Оценка за выполненное задание | Затруднения при выполнении |
| 1. Ответы на вопросы. | ||
| 2. Экспериментальное задание. | ||
| 3. Решение задач. |
VI. Рефлексия “Ракета”.
Наша ракета знаний мчится по галактике
“кинематика”. Окружите ее звездами:
На уроке все
было понятно, успел выполнить все задания,
доволен работой в группе, урок в целом удался
(красная звёздочка)
Большая часть нового
материала понятна, справился почти со всеми
заданиями, работа в группе прошла без особых
проблем. Был непонятен 1-2 момента (жёлтая
звёздочка).
Осталось много
непонятного, с большинством заданий не
справился, работой в группе не доволен. В целом
урок не понравился (синяя звёздочка).
Источник
