Первичная диаграмма растяжения это
Диаграмма растяжения показывает зависимость удлинения образца от продольной растягивающей силы.
Ее построение является промежуточным этапом в процессе определения механических характеристик материалов (в основном металлов).
Диаграмму растяжения материалов получают экспериментально, при испытаниях образцов на растяжение.
Для этого образцы стандартных размеров закрепляют в специальных испытательных машинах (например УММ-20 или МИ-40КУ) и растягивают до их полного разрушения (разрыва). При этом специальные приборы фиксируют зависимость абсолютного удлинения образца от прикладываемой к нему продольной растягивающей нагрузки и самописец вычерчивает кривую характерную для данного материала.
На рис. 1 показана диаграмма для малоуглеродистой стали. Она построена в системе координат F-Δl, где:
F — продольная растягивающая сила, [Н];
Δl — абсолютное удлинение рабочей части образца, [мм]

Рис. 1 Диаграмма растяжения стального образца
Как видно из рисунка, диаграмма имеет четыре характерных участка:
I — участок пропорциональности;
II — участок текучести;
III — участок самоупрочнения;
IV — участок разрушения.
Построение диаграммы
Рассмотрим подробнее процесс построения диаграммы.
В самом начале испытания на растяжение, растягивающая сила F, а следовательно, и деформация Δl стержня равны нулю, поэтому диаграмма начинается из точки пересечения соответствующих осей (точка О).
На участке I до точки A диаграмма вычерчивается в виде прямой линии. Это говорит о том, что на данном отрезке диаграммы, деформации стержня Δl растут пропорционально увеличивающейся нагрузке F.
После прохождения точки А диаграмма резко меняет свое направление и на участке II начинающемся в точке B линия какое-то время идет практически параллельно оси Δl, то есть деформации стержня увеличиваются при практически одном и том же значении нагрузки.
В этот момент в металле образца начинают происходить необратимые изменения. Перестраивается кристаллическая решетка металла. При этом наблюдается эффект его самоупрочнения.
После повышения прочности материала образца, диаграмма снова «идет вверх» (участок III) и в точке D растягивающее усилие достигает максимального значения. В этот момент в рабочей части испытуемого образца появляется локальное утоньшение (рис. 2), так называемая «шейка», вызванное нарушениями структуры материала (образованием пустот, микротрещин и т.д.).
Рис. 2 Стальной образец с «шейкой»
Вследствие утоньшения, и следовательно, уменьшения площади поперечного сечения образца, растягиваещее усилие необходимое для его растяжения уменьшается, и кривая диаграммы «идет вниз».
В точке E происходит разрыв образца. Разрывается образец конечно же в сечении, где была образована «шейка»
Работа затраченная на разрыв образца W равна площади фигуры образованной диаграммой. Ее приближенно можно вычислить по формуле:
W=0,8Fmax∙Δlmax
По диаграмме также можно определить величину упругих и остаточных деформаций в любой момент процесса испытания.
Для получения непосредственно механических характеристик металла образца диаграмму растяжения необходимо преобразовать в диаграмму напряжений.
Предел пропорциональности >
Примеры решения задач >
Лабораторные работы >
Источник
Первичная
диаграмма растяжения записывается в
координатах «Нагрузка Р
– абсолютное удлинение образца Δl».
По ней определяются основные механические
свойства, характеризующие прочность и
пластичность материала. При испытаниях
на растяжение прочностные свойства
определяются через напряжения σ,
вызывающие определенную упругую или
пластическую деформацию образца и
рассчитываются по формулам типа:
σ
= Р/F,
где
F
– площадь поперечного сечения образца.
В
системе СИ напряжения выражаются в
мегапаскалях [МПа]. Ранее повсеместно
использовалась размерность кг∙с/мм2,
которая еще сохранилась в ряде официальных
технических документов. Перевод единиц
осуществляется очень просто:
1 кг∙с/мм2 = 9,8 МПа ≈ 10 МПа.
По
указанному выше принципу на первичной
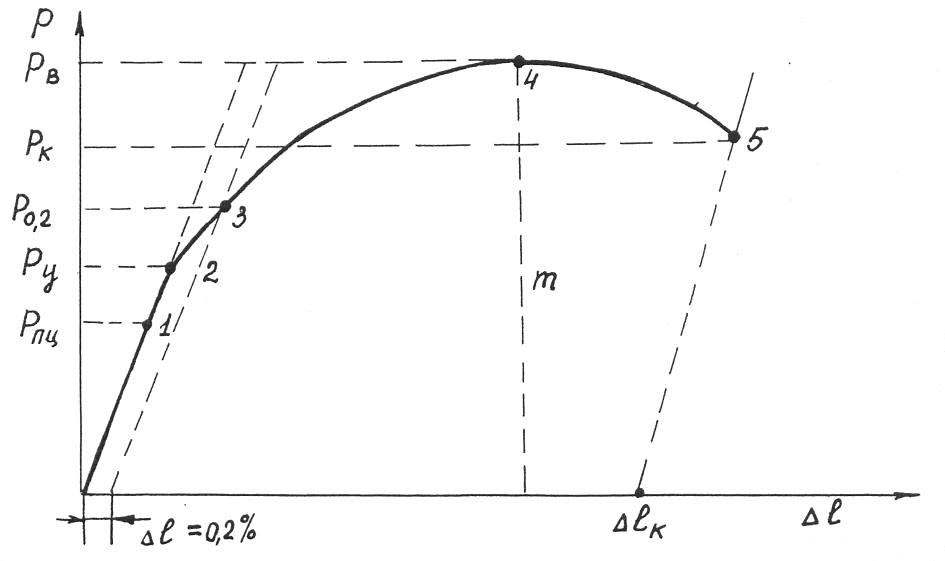
кривой растяжения можно выделить 5
основных точек – нагрузок для определения
соответствующих напряжений (рис. 3).
Рис. 3. |
(1)
Предел
пропорциональности
σПЦ
= РПЦ
/F0
– предельное напряжение, под действием
которого упругая деформация образца
подчиняется закону Гука (т. е. деформация
пропорциональна нагрузке). Для того,
чтобы унифицировать методику расчета,
σПЦоценивают
как условное напряжение при котором
отступление от линейной зависимости
между Р
и Δl
достигает заданной величины. Обычно
этот допуск задается через тангенс угла
наклона прямой, проходящей через
начальный участок кривой растяжения.
Стандартная величина отклонения –
50 %, возможно также использование
10 % и 25 %. Предел пропорциональности
в этих случаях соответственно обозначается
σПЦ50,
σПЦ25,
σПЦ10
[МПа].
(2)
Предел
упругости
σУ
= РУ
/F0
– напряжение,
при котором остаточная деформация
достигает определенной заданной величины
– обычно это 0,05 %. Используются также
меньшие величины вплоть до 0,005 %.
Принятая величина указывается в
обозначении условного предела упругости
σ0,05,
σ0,01 [МПа]
и т. д.
(3)
Предел
текучести
σ0,2
= Р0,2
/F0
– напряжение,
при котором остаточное удлинение
достигает определенной заданной величины
– обычно 0,2 %. Как видно это определение
полностью совпадает с предыдущим,
разница лишь в
величине допускаемого
остаточного
удлинения.
Поэтому перечисленные характеристики
– предел пропорциональности, предел
упругости и предел текучести более
строго следует называть условными,
т. е.
условный предел текучести и т. д.
В
отличие от условного существует
физический
предел текучести, который определяется
по положению площадки текучести на
кривой растяжения.
(4)
Временное
сопротивление
σВ
= РВ/F0
– напряжение, соответствующее предельной
нагрузке на кривой растяжения «Р
– Δl».
В этом расчете предельная нагрузка
относится к начальной площади сечения
образца F0
без учета ее изменения за счет пластической
деформации. Поэтому σВчасто
называется поаналогии
с предыдущими характеристиками «условный
предел прочности». Истинное напряжение
в этой точке равно SB
= PB/FB, где FВ– истинное
сечение образца.
σВи σ0,2являются
важнейшими характеристиками, определяющими
конструктивные свойства сплава.
Онивносятся в
ГОСТы и часто служат основой для
подразделения сплавов на группы, или
для маркировки сплавов. Например, серые
чугуны маркируются по величине σВ
и σ. Соответствие фактических значений
σВ, σ0,2требуемым по ГОСТ
определяет пригодность сплава для
эксплуатации.
(5)
Истинный
предел прочности
Точка
(5) соответствует разрушению образца.
Если в образце шейка не образуется, то
РК > РВ,
но при образовании шейки РК,как правило, всегда
меньше РВ.
Истинное напряжение, приводящее к
разрушению образца, т. е. истинный
предел прочности или истинное сопротивление
разрыву подсчитывается как SК
= PК/FК.
В конструкторских расчетах эта
характеристика не используется, т. к.
в процессе эксплуатации конструкции
не доводятся до разрушения. Но SКявляется
характеристикой физической прочности
материала.
По
первичной кривой растяжения (рис. 3)
определяют также основные характеристики
пластичности.
Относительное
удлинение
δ = (ΔlК/ Δl0) ∙ 100%,
где ΔlК
– длина образца, замеренная после
разрушения (ΔlК
= lК
–l0),
а l0
– расчетное
значение длины образца – база.
Относительное удлинение характеризует
способность сплава к равномерной
пластической деформации.
Относительное
сужение
= ((F0
– FK) / F0) ∙ 100%,
где IK
– площадь образца в месте разрушения.
Относительное сужение характеризует
предельную способность сплава к локальной
пластической деформации
и рассматривается как физический запас
пластичности.
Источник
Диаграммы нагружения и разгружения образцов.
Закон повторного нагружения
        Диаграмма растяжения образца позволяет оценить поведение материала образца в упругой и упруго-пластической стадиях деформирования, определить механические характеристики материала.
        Для получения численно сопоставимых между собой механических характеристик материалов диаграммы растяжения образцов перестраивают в диаграммы растяжения материалов, т.е. в зависимость между напряжением   и деформацией  , которые определяют по формулам
     ,
где - сила, действующая на образец,
     
 - начальная площадь поперечного сечения и начальная длина расчетной части образца.
        Диаграмма растяжения материала, полученная при этих условиях (без учета изменения размеров расчетной части образца), называется условной диаграммой растяжения материала в отличие от действительной диаграммы растяжения, которую получают с учетом изменений размеров образца.
        Диаграмма растяжения материала зависит от его структуры, условий испытаний (температуры, скорости деформирования).
   
        Диаграмма растяжения образца из низкоуглеродистой стали при однократном нагружении до разрушения. Конечная точка диаграммы соответствует разрушению.
        На начальном участке диаграммы между силой   и удлинением   соблюдается прямая пропорциональная зависимость — образец подчиняется
закону Гука. В точке А диаграммы закон Гука нарушается: зависимость между силой и удлинением становится нелинейной. На диаграмме наблюдается горизонтальный участок (участок БВ), называемый площадкой текучести. В этой стадии испытания образец удлиняется (деформируется) практически при постоянной силе. Это явление называется текучестью, при этом образец деформируется равномерно и по всей длине рабочей части. В точке В площадка текучести заканчивается и начинается участок упрочнения. В конечной точке Д этого участка достигается максимальная сила, которую может выдержать образец.
        При нагружении до предела пропорциональности (точка Г диаграммы) и при дальнешем уменьшении нагрузки образец разгружается по линейному закону, который совпадает с законом первичного нагружения. В этом заключается «закон разгрузки». При нагружении образца в пределах действия закона Гука законы нагружения и последующего разгружения совпадают. При полной разгрузке образца его размеры и форма возвращаются к первоначальной кривой однократного нагружения.
        Напряженное состояние образца до точки Д — одноосное.
        Далее начинается участок разрушения или участок местной текучести. Он характеризуется местным утонением образца и появлянием шейки.
        На конечном участке ДЕ (после возникновения шейки) происходит локализация деформаций в шейке, в остальной части образца они практически не увеличиваются. Деформация в шейке неоднородная, имеет существенный градиент вдоль оси образца. Напряженное состояние на этом участке становится неоднородным, кроме того, оно изменяется качественно — становится трехосным.
Диаметр шейки уменьшается по мере деформирования образца, и образец разрывается по наименьшему сечению шейки.
        Если при испытании на растяжение нагружение приостановить, например, в точке Г диаграммы и осуществить разгружение образца, то окажется, что диаграмма разгружения и диаграмма предыдущего нагружения не совпадают. Линия разгружения в этом случае — прямая, параллельная начальному линейному участку диаграммы растяжения образца. Такой характер деформирования образца при его разгружении называется законом разгружения.
При повторном нагружении диаграмма до точки Г совпадает с линией разгружения, а затем будет совпадать с диаграммой растяжения образца при однократном нагружении.
Такой характер деформирования называется законом повторного нагружения и заключается в пропорциональной зависимости силы и удлинения, которая сохраняется до значения силы, достигнутой при первичном нагружении.
         При разгружении образца в пределах участка ОА законы нагружения, разгружения и повторного нагружения совпадают.
Источник
В ходе опыта на растяжение был получен график зависимости удлинения от приложенной силы.
Позже были введены относительные величины, такие как напряжение и относительное удлинение. Благодаря этим величинам можно модифицировать исходный график из опыта так, что по нему сразу можно будет определить необходимые величины, безотносительно того, какую геометрию имел образец в опыте.
Однако сделать это можно двумя путями:
- Искать истинные напряжения и истинные относительные удлинения
- Для нахождения напряжений использовать только исходную площадь поперечного сечения; для нахождения относительного удлинения абсолютное удлинение делить на исходную длину недеформированного стержня
Несмотря на то, что первый способ является точным по своей сути, в инженерной практике используют упрощённый подход. Во-первых, для расчётов на прочность ищутся действующие и допускаемые напряжения и затем сравниваются. В случае применения истинной диаграммы для определения допускаемых напряжений, расчётчикам так же пришлось бы вычислять точные площади для определения истинных действующих напряжений, что является неоправданно трудоёмким процессом. Во-вторых, на интересующем линейном участке истинная и упрощённая инженерная диаграммы практически совпадают:
Выше показана диаграмма растяжения для некоторого стального образца: кривая В – истинная диаграмма, кривая A – инженерная диаграмма.
Если применить второй (упрощённый) способ к диаграммам из опыта, то характер кривых не изменится:
Всё это рассказывается потому, что в современной практике люди, делающие расчёты на прочность, при выборе допускаемых напряжений руководствуются НЕ диаграммой растяжения в целом, а лишь некоторыми характерными точками, снятыми с этой диаграммы.
Для каждого металлического материала в дальнейшем будем выделять две характерные точки на оси напряжений:
- Напряжение, выше которого образец будет иметь заметные остаточные деформации
- Напряжение, при котором образец воспринял наибольшую силу
Если взглянуть на график для стали, то можно заметить, что имеется такой участок, на котором начинает значительно расти удлинение, при этом сила практически не меняется. Материал как будто течёт. Назовём этот участок площадкой текучести, а соответствующее напряжение – пределом текучести. Явление текучести материала характерно для строительных сталей, бронзы, латуни. Обозначим это напряжение как σт:
На графике для алюминия такой площадки нет. Тем не менее введём некоторый условный предел, скажем, напряжение, при котором остаточная деформация равняется 0.002 мм/мм или 0.2%. Назовём его условным пределом текучести и обозначим как σ02. Условный предел текучести используется для титановых и алюминиевых сплавов:
Вторая характерная точка – это напряжение, при котором образец выдержал наибольшую силу. Согласно диаграмме растяжения, этому напряжению соответствует начало образования шейки в образце – локализованного уменьшения поперечного сечения. После этого предела сила начинает падать, потому образец продолжил удлиняться. Если же после этого предела растягивающая сила продолжит увеличиваться, то образец разрушится. Этот предел назовём пределом прочности или временным сопротивлением разрушению и будем обозначать σв или σпч:
Также иногда встречается и третья характерная точка – это напряжение, соответствующее окончанию начального линейного участка. Это напряжение называется пределом пропорциональности. Оно чуть меньше предела текучести и, строго говоря, пользоваться нужно именно им, а не пределом текучести. Однако для его определения нужны очень точные измерительные приборы. Потому общепринято пользоваться пределом текучести в качестве предела, выше которого будут значительные остаточные деформации.
Помимо характерных напряжений, имеется также и одна характерная деформация — это относительное удлинение при разрыве. Это отношение абсолютного удлинения образца при разрыве к исходной недеформированной длине. Эту величину чаще всего обозначают греческой буквой δ, её размерность либо мм/мм, либо в %. По этой величине можно судить о степени пластичности того или иного материала.
Примеры того, в каком виде расчётчик получает представления о механических свойствах материала:
Д16 (дюраль)
30ХГСА (легированная сталь)
Источник
ПОЛУЧЕНИЕ И АНАЛИЗ ДИАГРАММ РАСТЯЖЕНИЯ
Целью настоящей лабораторной работы является приобретение навыков записи, построения и анализа диаграмм деформации, а также изучение графического и аналитического способов определения основных характеристик прочности и пластичности при механических испытаниях на растяжение.
Испытания на растяжение являются самым распространенным видом статических механических испытаний. Для полной характеристики механических свойств образцы растягиваются до разрушения на специальных, часто универсальных, испытательных машинах (рис. 1), основными узлами которых являются механизм передачи на образец растягивающего усилия и механизм измерения силы сопротивления образца деформации. В процессе испытания зависимость силы сопротивления деформации от величины абсолютного удлинения образца фиксируется в двухкоординатной системе: усилие P – удлинение Dl. Эта зависимость представляет собой результат испытания и называется первичной диаграммой растяжения.
Многообразие первичных диаграмм растяжения для различных материалов можно в первом приближении свести к нескольким типам. На рис. 2 показаны разновидности первичных диаграмм растяжения. Диаграммы могут не отражать резкий переход от упругой деформации к пластической (рис. 2, а, б, в), но могут и отражать (рис. 2, г, д, е). Во втором случае переход имеет вид горизонтального участка, называемого площадкой текучести, или проявляется в виде зуба текучести.
Рис. 2. Первичные диаграммы растяжения: а – хрупкое растяжение; б – разрушение после равномерной деформации; в – разрушение после образования шейки; г, д, е – определение нагрузки Pт для расчета физического предела текучести в зависимости от вида диаграмм.
Испытания на растяжение согласно ГОСТ 1497-73 проводятся на цилиндрических или плоских образцах различных размеров. В качестве основных применяются цилиндрические образцы с диаметром рабочей части d0 = 10 мм и начальной расчетной длиной l0 = 10d0 или l0 = 5d0. Образцы изготавливаются на металлорежущих станках и имеют гладкие или резьбовые головки для установки в захватах испытательной машины. Скорость перемещения подвижного захвата, выражаемая в мм/мин, может быть разной, но, как правило, не превышает 0,4 от расчетной длины образца.
Скорость деформации образца VД, с–1, можно оценить следующим образом:
, (1)
где VЗ – скорость движения захватов испытательной машины, мм/мин;
l=l0+d0 – рабочая длина образца, мм.
Для возможности сравнения результатов испытаний различных по размерам образцов бывает целесообразно установить связь между условными напряжениями s и относительным удлинением d. Вид диаграммы растяжения при переходе к координатам s – d не меняется.
Определение механических свойств производится как непосредственно во время испытания (для определения предела пропорциональности и предела упругости этот способ предпочтительнее), так и после испытания. Во втором случае исходными материалами являются диаграмма растяжения и разрушившийся образец. В данной лабораторной работе определение механических свойств проводится после испытания графическим методом по диаграмме растяжения.
Расчет прочностных свойств
Диаграмма растяжения позволяет определять прочностные свойства сопротивления как малым пластическим деформациям (sПЦ – предел пропорциональности, sу – предел упругости, sт – предел текучести), так и большим пластическим деформациям (sв – предел временного сопротивления или предел прочности). Прочностные свойства выражаются в условных напряжениях, рассчитанных по формуле:
, (2)
где Pi– растягивающая нагрузка, F0 – площадь поперечного сечения до испытания. В системе СИ нагрузку P выражают в ньютонах, площадь поперечного сечения – в м2. Прочностные механические свойства чаще всего выражают в мегапаскалях при соотношении:
1 МПа = 106 Н/м2 = 1 МН/м2.
В заводской практике чаще используется оценка прочности в кг/мм2 или кгс/мм2, равная 1 кг/мм2 = 10 МПа.
Предел пропорциональности sПЦ – условное напряжение, соответствующее отклонению от линейного хода диаграммы растяжения, задаваемого определенным допуском (10%, 25%, 50%) на уменьшение тангенса угла наклона кривой к оси удлинения. Величина допуска указывается в обозначении предела пропорциональности: sПЦ50, sПЦ25, sПЦ10.
При определении предела пропорциональности графически на диаграмме растяжения вначале продолжают прямолинейный участок упругой деформации до пересечения с осью абсцисс в точке О’ (рис. 3), которую принимают за новое начало координат, исключая таким образом искаженный из-за недостаточной жесткости машины начальный участок диаграммы. Далее на произвольной высоте в пределах упругой области проводят прямую АВ, перпендикулярную оси нагрузок. На ее продолжении вправо откладывают отрезок ВС = 0,5 АВ и проводят линию ОС. Если теперь провести касательную DЕ к кривой растяжения параллельно ОС, то точка касания F определит нагрузку PПЦ и предел пропорциональности может быть определен:
(3)
Предел упругости sу – условное напряжение, соответствующее появлению остаточной деформации определенной, заданной величины. Обычно остаточная деформация составляет 0,05% от расчетной длины образца lo, но этот допуск может быть и меньше, вплоть до 0,001%. Использованный при расчете допуск указывается в обозначении условного предела текучести: s0,05, s0,001 и т. п.
Для определения, например, s0,05 вычисляется величина заданного остаточного удлинения, исходя из расчетной длины образца. Найденная величина увеличивается пропорционально масштабу диаграммы по оси деформаций (обычно не менее 50:1) и отрезок полученной длины О’B откладывается по оси абсцисс вправо от точки О’ (рис. 4). Из точки B проводится прямая, параллельная упругому участку диаграммы О’А. Точка пересечения F с кривой растяжения определяет нагрузку P0,05, отвечающую пределу упругости:
(4)
Рис. 3. Графический способ определения предела пропорциональности.
Условный предел текучести s0,2 – условное напряжение, при котором остаточная деформация достигает определенной величины, обычно 0,2% от рабочей длины образца. Допуск на остаточное удлинение может быть и другим, например, 0,1% или 0,3%.
Рис. 4. Графический способ определения предела упругости.
Методика определения условного предела текучести по диаграмме растяжения аналогична методике определения предела упругости. Вычисляют величину заданного остаточного удлинения, исходя из рабочей длины образца (l=l0+d0). Найденная величина увеличивается пропорционально масштабу диаграммы по оси деформаций, и отрезок полученной длины откладывается по оси абсцисс вправо от точки О’ (рис. 4).
Отрезок О’B, таким образом, равен 0,002·l·M, где М – масштаб по оси удлинений. Ордината точки пересечения F прямой, параллельной ОА, с кривой растяжения определяет в этом случае нагрузку P0,2, отвечающую пределу текучести:
(5)
Физический предел текучести sт – условное напряжение, соответствующее наименьшей нагрузке площадки текучести, когда деформация образца происходит без увеличения нагрузки. В этом случае диаграмма деформации имеет вид, подобный указанному на рис. 2, г, д, позволяющий определять физический предел текучести, как
(6)
Когда имеется зуб текучести (рис. 2, е), вводится понятие о верхнем sтв и нижнем sтн пределах текучести.
Временное сопротивление или предел прочности sв условное напряжение, соответствующее наибольшей нагрузке Pmax на диаграмме растяжения (рис. 2, а, б, в). Временное сопротивление вычисляется по формуле:
(7)
Расчет пластических свойств
Для расчета пластических свойств предпочтительно иметь образец после испытания. Части образца складываются в месте разрыва так, чтобы между ними не было зазора. На таком сложенном образце измеряется длина расчетной части lк после разрыва и минимальный диаметр dк в двух взаимно перпендикулярных направлениях в месте разрыва.
Относительное удлинение d , %, определяется по формуле:
(8)
В случае образования шейки эта величина зависит от размеров образца. При этом относительное удлинение d имеет индекс: d2,5, d5, d10, указывающий кратность образца – отношение расчетной длины до испытания к диаметру образца до испытания (l0/d0).
Относительное сужение y, %, определяется по формуле:
, (9)
где Fк вычисляется по среднему арифметическому значению dк.
Расчет пластических свойств возможен и по диаграмме растяжения. Более того, именно он позволяет из общих свойств пластичности d и y выделить dравн и yравн, характеризующие способность материала к равномерной деформации, т.е. к накапливанию ее во всем объеме, без локализации. Способность к равномерной деформации более физически обоснованно характеризует пластичность материала, чем общие свойства d и y в случае, если при испытании образец разрушается с образованием шейки. Чем больше доля сосредоточенной деформации (т.е. чем короче образец), тем в большей степени d и y характеризуют именно ее, а не предельную пластичность материала.
Для разделения относительного удлинения на равномерное и сосредоточенное на диаграмме растяжения проводят линии параллельно упругому участку диаграммы из точек максимальной и предельной нагрузки до пересечения с осью абсцисс, как это опказано на рис. 2, в. Определенные по оси удлинений отрезки с учетом масштаба – это абсолютные величины удлинения образца в процессе равномерной деформации (Dlравн) и в процессе образования шейки (Dlсоср).
Равномерное относительное удлинение dравн, %, определяется по формуле:
(10)
Сосредоточенное относительное удлинение dсоср, %, определяется по формуле:
(11)
Равномерное относительное сужение yравн, %, определяется из соотношения:
(12)
Это соотношение следует из закона постоянства объема: l0F0= lравнFравн, справедливого в области равномерной деформации.
Сосредоточенное относительное сужение yсоср, %, находят из разницы:
yсоср = y – yравн . (13)
Таким образом, если образец при испытании деформировался равномерно вплоть до разрушения (рис. 2, б, образец при растяжении не дошел до образовании шейки), то свойства d и y одинаково характеризуют предельную пластичность материала. Если шейка образуется, то целесообразно отдельно определять равномерное и сосредоточенное относительное удлинение. Кроме того, в этом случае для характеристики предельной способности материала к пластическому растяжению более правильно использовать относительное сужение y, признавая его характеристикой, в основном, сосредоточенной деформации. Для пластичных материалов yсоср может составлять до 80% и более от общей величины y.
Построение диаграмм растяжения в истинных координатах
Диаграммы растяжения в истинных координатах строятся для более строгого анализа свойств и деформационного упрочнения при растяжении. Они строятся в координатах истинные напряжения – истинные деформации. Истинные напряжения получают, учитывая изменение сечения при деформации и относя нагрузку не к исходному сечению, а к сечению в каждый данный момент деформации. Следовательно, чем пластичнее материал, тем в большей степени истинные напряжения отличаются от условных.
Построение диаграммы растяжения в истинных координатах требует многократного измерения диаметра образца в процессе испытания. Одновременно с измерением диаметра образца диаграмма растяжения получает отметку, по числу которых она разделяется на ряд участков – этапов испытания. На каждом этапе вычисляется площадь поперечного сечения Fi и определяется нагрузка Pi. Истинное напряжениеSiрассчитывается по формуле:
. (14)
Величина истинных деформаций определяется как истинное относительное удлинение ei
, (15)
если измерялась длина расчетной части образца в процессе испытания, либо как истинное относительное сужение ji
. (16)
Возможный вид диаграммы растяжения в истинных координатах показан на рис. 5. На стадии упругой деформации диаграмму часто изображают совпадающей с осью ординат, на которой откладывается предел текучести, практически одинаковый в условных и истинных значениях напряжений ввиду незначительности изменения размеров образца при этих напряжениях.
Построение диаграмм растяжения в истинных координатах позволяет рассчитывать истинное сопротивление разрыву Sк – характеристику прочности, определяемую как отношение нагрузки в момент разрушения к площади поперечного сечения образца в месте разрыва:
, (17)
а также пластические свойства –
истинное относительное удлинение (18)
истинное относительное сужение . (19)
Рис. 5. Диаграмма растяжения в истинных координатах.
Весьма существенно, что на основании диаграммы можно оценить способность материала к деформационному упрочнению, называемую коэффициентом (или модулем) деформационного упрочнения. Коэффициент деформационного упрочнения К = tg a. он может быть различным на разных стадиях растяжения (рис. 5). Средний для всего процесса коэффициент упрочнения может быть определен:
. (20)
Итак, необходимо отчетливо представлять физический смысл рассчитываемых механических характеристик. Если пластические свойства характеризуют способность материала к равномерной или сосредоточенной деформации, а прочностные свойства sпц, sу, sт являются показателями сопротивления материала малым пластическим деформациям, то трактовка таких свойств, как sв и Sк значительно шире. Так, величина sв имеет строгий физический смысл лишь при почти полном отсутствии пластической деформации, когда диаграмма растяжения имеет вид, подобный показанному на рис. 2, а. В этом случае имеет место хрупкое разрушение, sв » Sк и являются характеристиками сопротивления разрушению в условиях растяжения, т.е. хрупкой прочностью.
Для более пластичных материалов (рис. 2, б, в) sв – не более чем условное напряжение в момент разрушения или условное напряжение, соответствующее максимальной нагрузке. В том и другом случае величину sв можно считать условной характеристикой сопротивления значительной, но равномерной деформации растяжением. Величина Sк для материалов, проявляющих пластичность, достаточно строго характеризует предельную прочность материала лишь в случае рис. 2, б, поскольку образец равномерно деформируется в условиях не изменяющегося напряженного состояния вплоть до разрыва.
В случае рис. 2, в, т.е. при образовании шейки, схема одноосного растяжения меняется на сложное напряженное состояние, и расчет по формуле (17) означает, что Sк > sв и характеризует лишь некое среднее продольное напряжение в момент разрушения, т.е. сопротивление значительным пластическим деформациям.
Вышесказанное означает, что при сопоставлении прочностных свойств sв и Sк различных материалов следует учитывать конкретный смысл этих характеристик для каждого материала, проявляющийся в том или ином виде его диаграммы растяжения.
Задание к лабораторной работе
1. Записать диаграмму растяжения на разрывной машине. В процессе записи делать остановки (i = 8-10), не снимая нагрузки, измеряя на каждой остановке диаметр образца и записывая значение диаметра и соответствующей нагрузки. Результаты измерений и расчетов занести в табл. 1.
2. Произвести расчет прочностных и пластических свойств по методике из соответствующих разделов руководства.
3. По данным табл. 1 построить диаграммы растяжения в условных s = f (y) и истинных S = f (j) координатах.
4. Рассчитать Sк, eк, jк и K.
5. Заполнить таблицу механических свойств по форме табл. 2.
6. Оформить отчет по работе.
Таблица 1
Расчетные данные для построения диаграммы растяжения
в условных и истинных координатах
| Точка, i | di, мм | Fi, мм2 | yi= (F0–Fi)/Fi | ji=ln (F0/Fi) | Pi, Н | si=Pi/F0, МПа | Si=Pi/Fi, МПа |
Таблица 2
Механические свойства
при растяжении материала _______________
температура испытания _______________
скорость испытания _______________
Источник