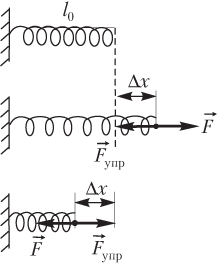
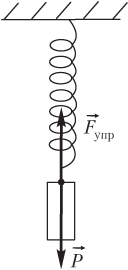Первая пружина жесткостью k имеет растяжение x вторая пружина
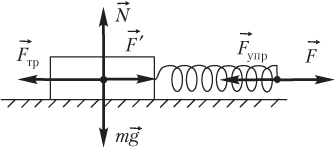
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Сила упругости — это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Силы, возникающие при пластических деформациях, не относятся к силам упругости.
Понятие о деформациях
Деформация — это изменение формы и размеров тела.
К деформациям относятся: растяжение, сжатие, кручение, сдвиг, изгиб.
Деформации бывают упругими и пластическими.
Закон Гука
Абсолютная величина силы упругости прямо пропорциональна величине деформации. В частности, для пружины, сжатой или растянутой на величину (displaystyle x) (разница между крайними положениями), сила упругости задается формулой [F=kx] где (displaystyle k) — коэффициент жесткости пружины.
Единицы измерения коэффициента жесткости: (k=)[Н/м].
Закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела.
На штативе закреплён школьный динамометр. К нему подвесили груз массой 0,1 кг. Пружина динамометра при этом удлинилась на 2,5 см. Чему будет равно удлинение пружины, если масса груза увеличится втрое? (Ответ дайте в сантиметрах)
Согласно закону Гука [F=kDelta x] где k – жесткость пружины, ( Delta x) – удлинение пружины.
Найдем жесткость пружины, зная, что ( Delta x) = 2,5 см = 0,025 м при приложении силы, равно ( F=m_1g=0,1cdot 10=1text{ H} ): [k=dfrac{F}{Delta x}=dfrac{1}{0,025}=40text{ H/кг}] Если массу груза увеличить в 3 раза, то есть, (m_2=0,3) кг, то удлинение пружины будет равно: [Delta x=dfrac{F}{k}=dfrac{m_2g}{k}=dfrac{3cdot0,1cdot10text{ H}}{40text{ H/кг}}=0,075text{ м}=7,5text{ см}]
Ответ: 7,5
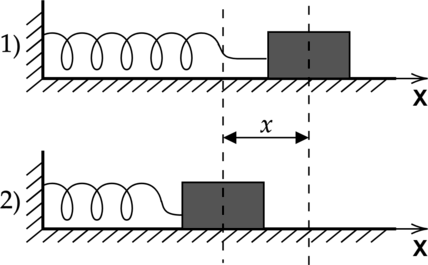
К системе из кубика массой M = 3 кг и двух пружин приложена постоянная горизонтальная сила F величиной 20 Н (см. рисунок). Между кубиком и опорой трения нет. Система покоится. Жёсткость первой пружины (k_1 = 400 text{ Н/м}). Жёсткость второй пружины (k_2 = 800 text{ Н/м}). Каково удлинение первой пружины? (Ответ дайте в сантиметрах)
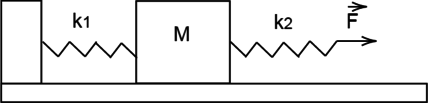
Согласно закону Гука удлинение (Delta x) пружины связано с ее жесткостью k и приложенной к ней силе F выражением (F=kDelta x). На первую пружину действует такая же сила F, что и на вторую, так как трения между кубиком и опорой нет. То, что первая пружина соединена со второй через кубик, здесь не имеет никакого значения, соответственно удлинение первой пружины – это величина, равная: [Delta x=dfrac{F}{k_1}=dfrac{20text{ H}}{400text{ H/м}}=0,05 text{ м}=5 text{ см}]
Ответ: 5
Определите силу, под действием которой пружина жёсткостью 200 Н/см удлинится на 5 мм.
Согласно закону Гука ( F=kDelta x ), где k – жесткость пружины, ( Delta x) – удлинение пружины, получаем: [F=kDelta x=(dfrac{200}{0,01})text{H/м}cdot(5cdot10^{-3})text{м}=100text{ H}]
Ответ: 100
Пружина одним концом прикреплена к неподвижной опоре, к другому концу приложили силу равную 1500 Н, при этом пружина растянулась на 0,2 м. Определите жесткость данной пружины. Ответ дать в Н/м.
После растяжения, пружина покоится и на неё действуют 2 силы направленные в противоположные направления: (F_{text{упр}}) – сила упругости и F – приложенная сила.
Тогда по первому закону Ньютона: [F_{text{упр}}=F] По закону Гука: [F_{text{упр}}=kx] Приравниваем эти формулы: [F=kx] Тогда [k=frac{F}{x}=frac{1500}{0,2}=7500 text{ Н/м}]
Ответ: 7500
К потолку прикреплены одним концом две пружины с одинаковой жесткостью. За другой конец первую пружину растягивают с силой (F_{text{1}}), которая в 2,5 раза больше силы (F_{text{2}}), растягивающей вторую пружину. При этом вторая пружина растянулась на 0,4 м. Насколько растянулась первая пружина? Ответ дать в метрах.
После растяжения обе пружины находятся в покое и на них, кроме данных сил действует сила упругости. Тогда по первому закону Ньютона: [F_{text{упр1}}=F_{text{1}}] [F_{text{упр2}}=F_{text{2}}] где (F_{text{упр1}}) – сила упругости, действующая на первую пружина, (F_{text{упр2}}) – на вторую.
По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [kx_{1}=F_{1}quad(1)] [kx_{2}=F_{text{2}}quad(2)] где (x_{1}) – удлинение первой пружины, (x_{2}) – второй. Разделим (1) на (2), получится: [frac{x_{1}}{x_{2}}=frac{F_{text{1}}}{F_{text{2}}}Rightarrow x_{1}=dfrac{F_{text{1}}x_{2}}{F_{text{2}}}=2,5cdot0,4=1text{ м}]
Ответ: 1
К грузу массой (m) аккуратно подвесили другой груз массой (M), при этом пружина с жесткостью 1200 Н/м удлинилась так, как показано на рисунке. Найдите массу (M). Ускорение свободного падения считать равным 10 м/(c^{2}). Ответ дать в кг.
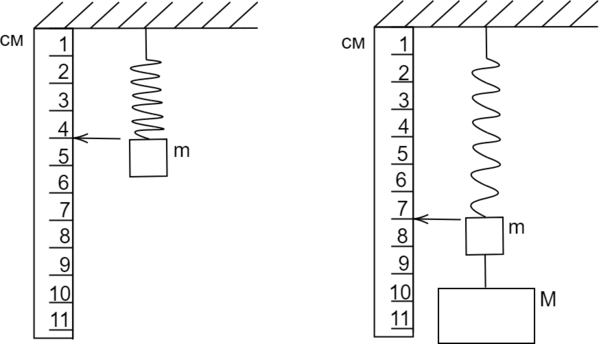
Рассмотрим ситуацию до подвешивания груза: система тел “груз и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg=F_{text{упр}1}] Рассмотрим ситуацию после подвешивания груза: систама тел “2 груза и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg+Mg=F_{text{упр2}}] По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [mg=kx_{1}quad(1)] [mg+Mg=kx_{2}quad(2)] Вычтем (1) из (2), получится: [Mg=k(x_{2}-x_{1})Rightarrow M=dfrac{k(x_{2}-x_{1})}{g}=frac{1200cdot0,03}{10}=3,6text{ кг}]
Ответ: 3,6
Источник
2.2. Силы
2.2.5. Сила упругости
Силы упругости возникают при деформации тел.
Вычисление силы упругости производится по закону Гука:
Fупр = k∆x,
где k — коэффициент жесткости (упругости) пружины; Δx=|l−l0| — абсолютная деформация (растяжения или сжатия) пружины, l0 — длина пружины в недеформированном состоянии, l — длина растянутой (или сжатой) пружины.
Направление силы упругости F→упр (рис. 2.9) противоположно направлению силы, вызывающей деформацию:
F→упр=−F→.
Рис. 2.9
Относительная деформация определяется отношением:
ε=Δxl0 или ε=Δxl0⋅100 %,
где Δx=|l−l0| — абсолютная деформация (растяжения или сжатия) пружины, l0 — длина недеформированной пружины, l — длина растянутой (сжатой) пружины.
Коэффициент жесткости (упругости) k нескольких пружин одинаковой длины, но разной жесткости вычисляется для последовательного соединения по формуле (рис. 2.10)
1k=1k1+1k2+…+1kN;
где k1, k2, …, kN — коэффициенты жесткости (упругости) этих пружин.
Рис. 2.10
Коэффициент жесткости (упругости) k нескольких пружин одинаковой длины, но разной жесткости (рис. 10), вычисляется для параллельного соединения по формуле (рис. 2.11)
k = k1 + k2 + … + kN,
где k1, k2, …, kN — коэффициенты жесткости (упругости) этих пружин.
Рис. 2.11
Для вычисления результирующих коэффициентов жесткости (упругости) параллельного и последовательного соединения одинаковых пружин удобно пользоваться формулами:
- для последовательного соединения N одинаковых пружин с коэффициентами жесткости (упругости) k0:
k=k0N;
- для параллельного соединения N одинаковых пружин с коэффициентами жесткости (упругости) k0:
k = k0N.
Пример 16. При последовательном соединении трех пружин, коэффициенты жесткости которых относятся как 1 : 2 : 3, сила 12 Н вызвала растяжение системы на 4,0 см. Рассчитать коэффициенты жесткости указанных пружин.
Решение. Величина силы упругости, действующей на пружину, определяется формулой
Fупр = kобщ∆x,
где kобщ — коэффициент жесткости составной пружины; ∆x — указанное в условии задачи растяжение пружины.
Величина силы упругости, с другой стороны, совпадает с величиной приложенной силы:
Fупр = F.
Значение данной силы и величина растяжения пружины под действием этой силы позволяют рассчитать коэффициент жесткости составной пружины:
kобщ=FΔx=124,0⋅10−2=300 Н/м.
Для определения коэффициентов жесткости каждой пружины запишем их коэффициенты жесткости в следующем виде:
- для первой пружины
k1 = k;
- для второй пружины
k2 = 2k;
- для третьей пружины
k3 = 3k,
так как указанные коэффициенты по условию задачи соотносятся между собой как
k1 : k2 : k3 = 1 : 2 : 3.
Для расчета величины k запишем формулу для коэффициента жесткости пружины, состоящей из трех последовательно соединенных пружин, и подставим в нее выражения k1, k2, k3:
1kобщ=1k1+1k2+1k3=1k+12k+13k=116k, или kобщ=6k11.
Найденное ранее значение kобщ = 300 Н/м позволяет рассчитать k = 550 Н/м.
Тогда коэффициенты жесткости каждой из пружин имеют значения:
- для первой пружины
k1 = k = 550 Н/м;
- для второй пружины
k2 = 2k = 1100 Н/м;
- для третьей пружины
k3 = 3k = 1650 Н/м.
Пример 17. Вычислить абсолютную деформацию пружины с коэффициентом жесткости 100 Н/м, присоединенной к бруску, лежащему на горизонтальной поверхности, в момент начала скольжения бруска по поверхности. Сила, вызывающая скольжение бруска, прикладывается к пружине. Коэффициент трения между бруском и поверхностью равен 0,1. Масса бруска составляет 1,0 кг.
Решение. На рисунке показаны силы, действующие на брусок.
Абсолютную деформацию пружины рассчитаем по формуле
Δx=Fупрk,
где Fупр = F — модуль силы упругости, возникающей в пружине (величина силы упругости равна величине приложенной силы); k — коэффициент жесткости пружины.
Со стороны пружины на брусок действует сила, модуль которой совпадает с силой упругости:
F′=Fупр=F.
В момент начала скольжения величина силы трения равна силе, приложенной к бруску в направлении движения:
Fтр=F′=μN,
где µ — коэффициент трения; N = mg — модуль силы нормальной реакции опоры.
Поэтому величина силы упругости может быть вычислена по формуле
Fупр = µmg.
Из исходного уравнения следует, что величина деформации пружины в момент начала скольжения определяется выражением
Δx=μmgk.
Расчет позволяет определить ее значение:
Δx=0,1⋅1,0⋅10100=10−2 м=1,0 см.
Пример 18. Вычислить массу груза, подвешенного к пружине жесткостью 250 Н/м, если известно, что относительная деформация пружины составляет 25 %. Длину нерастянутой пружины считать равной 100 мм.
Решение. Проиллюстрируем условие задачи рисунком.
Сила упругости определяется формулой
Fупр = k∆x,
где k — коэффициент жесткости (упругости) пружины; ∆x = l − l0 — абсолютная деформация пружины (величина ее растяжения под действием груза); l0 — длина недеформированной пружины; l — длина пружины в деформированном состоянии.
Из определения относительной деформации
ε=Δxl0
следует, что
∆x = εl0,
где ε = 0,25 — относительная деформация (в долях).
С учетом значения относительной деформации формула для вычисления силы упругости принимает вид:
Fупр=kεl0=0,25kl0.
С другой стороны, сила упругости, возникающая в пружине, численно равна весу тела, вызвавшего деформацию пружины:
Fупр = P = mg,
где m — масса тела; g — модуль ускорения свободного падения.
Таким образом, имеем равенство
0,25kl0 = mg,
позволяющее вычислить массу груза, подвешенного к пружине:
m=0,25kl0g=0,25⋅250⋅0,10010=0,625 кг=625 г.
Источник