Первая пружина жесткостью k имеет растяжение x
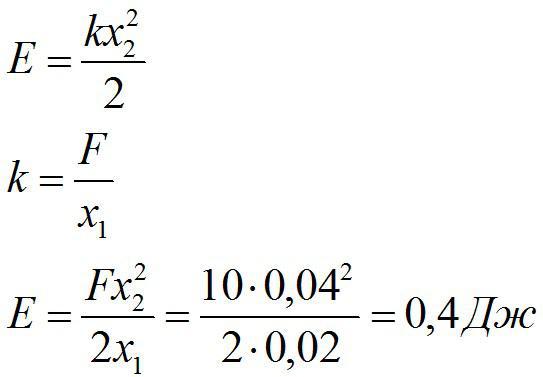
I вариант
Часть А.
1. Тело массой m движется со скоростью V. Каков импульс тела?
А. mV². Б. mV². В. mV . Г. mV . Д. mV . Е. mV .
2 2 2 2
2. Тело массой m движется со скоростью V. Какова кинетическая энергия тела?
А. mV². Б. mV². В. mV . Г. mV . Д. mV . Е. mV .
2 2 2 2
3. Тело массой m поднято над поверхностью Земли на высоту h. Какова потенциальная
энергия тела?
А. mg. Б. mgh . В. mh . Г gh . Д. mg .
h
4. Пружина жескостью k под действием силы F растянута на x м. Какова потенциальная
энергия упругой деформации пружины?
А. kx. Б. kx². В. kx. Г. kx². Д. mgh .
2 2
5. Мяч был брошен с поверхности Земли вертикально вверх. Он достиг высшей точки
траектории и затем упал на Землю. В какой момент времени движения полная
механическая энергия мяча имела максимальное значение? Сопротивлением воздуха
пренебречь.
А. В момент начала движения вверх. Б. В момент достижения верхней точки траектории. В. В момент прохождения половины расстояния до верхней точки траектории. Г. В
момент падения на Землю. Д. В течение всего времени полёта полная механическая
энергия была одинакова.
6. Два шара с одинаковыми массами m двигались навстречу друг другу с одинаковыми по
модулю скоростями V. После неупругого столкновения оба шара остановились. Каково
изменение суммы импульсов двух шаров в результате столкновения?
А. mV . Б. 2mV . В. 0 . Г.- mV . Д. — 2mV .
7. Камень брошен вертикально вверх. На пути 1 м его кинетическая энергия уменьшилась
на 16 Дж. Какую работу совершила сила тяжести на этом пути?
А. — 16 Дж. Б.- 4 Дж. В. 16 Дж. Г. 4 Дж. Д. 0 Дж.
8. Какова кинетическая энергия автомобиля массой 1000 кг, движущегося со скоростью 36
км/ч?
А. 36 · 10³ Дж. Б. 648 · 10³ Дж. В. 10 Дж. Г. 5· 10 Дж.
Часть В.
1. Тело поднимается вертикально вверх под действием силы F = 10Н. В начальный момент
времени тело находилось на высоте, равной 1м, от поверхности Земли. Найдите
положение тела в тот момент, когда сила, поднимающая груз, совершила работу,
равную 200 Дж.
2. Недеформированную пружину растягивают на ∆l = 10см. Найдите работу
деформирующей пружину силы, если при растяжении пружины на ∆l˳ = 1см требуется
сила F˳= 4Н. Чему равна работа силы упругости пружины?
II вариант
Часть А.
1. Как называется физическая величина, равная произведению массы тела на вектор его
мгновенной скорости?
А. Импульс тела. Б. Импульс силы. В. Кинетическая энергия. Г. Потенциальная энергия. Д. Двойная кинетическая энергия.
2. Как называется физическая величина, равная половине произведения массы тела на
квадрат его мгновенной скорости?
А. Импульс тела. Б. Импульс силы. В. Кинетическая энергия. Г. Потенциальная энергия. Д. Двойная кинетическая энергия.
3. Как называется физическая величина, равная произведению массы тела m на ускорение
свободного падения и на расстояние h от тела до поверхности Земли?
А. Импульс тела. Б. Импульс силы. В. Кинетическая энергия. Г. Потенциальная энергия. Д. Двойная кинетическая энергия.
4. Растяжение пружины жесткостью k увеличено на ∆x. Как изменилась при этом
потенциальная энергия упругой деформации пружины?
А. Увеличилась на k∆x. Б. Увеличилась на k∆x². В. Увеличилась на k∆x² .
2
Г. Уменьшилась на k∆x. Д. Уменьшилась на k∆x² . Е. Уменьшилась на k∆x² .
2
5. Мяч был брошен с поверхности Земли вертикально вверх. Он достиг высшей точки
траектории и затем упал на Землю. В какой момент времени движения полная
механическая энергия мяча имела минимальное значение? Сопротивлением воздуха
пренебречь.
А. В момент достижения верхней точки траектории. Б. В течение всего времени полёта
полная механическая энергия была одинакова. В. В момент падения на Землю. Г. В
момент прохождения половины расстояния до верхней точки траектории. Д. В момент
начала движения вверх.
6. Два шара с одинаковыми массами m двигались навстречу друг другу с одинаковыми по
модулю скоростями V. После упругого столкновения каждый шар стал двигаться в
обратном направлении с прежней по модулю скоростью. Каково
изменение суммы импульсов двух шаров в результате столкновения?
А. mV . Б. — 2mV . В. 4mV . Г.- 4mV . Д. 0 .
7.. Камень брошен вертикально вверх. На пути 1 м его кинетическая энергия увеличилась
на 16 Дж. Какую работу совершила сила тяжести на этом пути?
А. — 16 Дж. Б.- 4 Дж. В. 16 Дж. Г. 4 Дж. Д. 0 Дж.
8. Какова кинетическая энергия ракеты массой 100 кг, движущегося со скоростью 60
км/мин?
А. 10⁸ Дж. Б. 5 · 10⁷ Дж. В. 1,8 · 10 Дж. Г. 6 · 10³ Дж. Д. 50 Дж.
Часть В.
1. Тело поднимается вертикально вверх под действием силы F = 10Н. В начальный момент
времени тело находилось на высоте, равной 1м, от поверхности Земли. Найдите
положение тела в тот момент, когда сила, поднимающая груз, совершила работу,
равную 300 Дж.
2. Недеформированную пружину растягивают на ∆l = 10см. Найдите работу
деформирующей пружину силы, если при растяжении пружины на ∆l˳ = 1см требуется
сила F˳= 6Н. Чему равна работа силы упругости пружины?
Контрольное тестирование
по дисциплине физика
Коды правильных ответов:
Часть А | Часть В | |||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 1 | 2 | |
1 вариант | Д | Б | Б | Г | Д | В | А | Г | 21 | 2 |
2 вариант | А | В | Г | В | Б | Д | В | Б | 31 | 3 |
Шкала оценки знаний обучающихся по итогам выполнения теста:
Число правильных ответов | 0-2 | 3-4 | 5-6 | 7-8 | 9-10 |
Оценка в баллах | 1 | 2 | 3 | 4 | 5 |
Источник
Можно не знать закон Ома и сидеть дома. Но если не знаешь закон Гука – лучше тоже не выходить. Особенно, если идешь на экзамен по физике.
Здесь устраняем пробелы в знаниях и разбираемся, как решать задачи на силу упругости и применение закона Гука. А за полезной рассылкой для студентов добро пожаловать на наш телеграм-канал.
Сила упругости и закон Гука: определения
Сила упругости – сила, препятствующая деформациям и стремящаяся восстановить первоначальные форму и размеры тела.
Примеры действия силы упругости:
- пружины сжимаются и разжимаются в матрасе;
- мокрое белье колышется на натянутой веревке;
- лучник натягивает тетиву, чтобы выпустить стрелу.
Простейшие деформации – деформации растяжения и сжатия.
Закон Гука:
Деформация, возникающая в упругом теле под действием внешней силы, пропорциональна величине этой силы.
Коэффициент k – жесткость материала.
Есть и другая формулировка закона Гука. Введем понятие относительной деформации «эпсилон» и напряжения материала «сигма»:
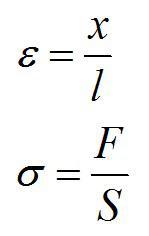
S – площадь поперечного сечения деформируемого тела. Тогда закон Гука запишется так: относительная деформация пропорциональна напряжению.
Здесь Е – модуль Юнга, зависящий от свойств материала.
Закон Гука был экспериментально открыт в 1660 году англичанином Робертом Гуком.
Вопросы на силу упругости и закон Гука
Вопрос 1. Какие бывают деформации?
Ответ. Помимо простейших деформаций растяжения и сжатия, бывают сложные деформации кручения и изгиба. Также разделяют обратимые и необратимые деформации.
Вопрос 2. В каких случаях закон Гука справедлив для упругих стержней?
Ответ. Для упругих стержней (в отличие от эластичных тел) закон Гука можно применять при малых деформациях, когда величина эпсилон не превышает 1%. При больших деформациях возникают явления текучести и необратимого разрушения материала.
Вопрос 3. Как направлена сила упругости?
Ответ. Сила упругости направлена в сторону, противоположную направлению перемещения частиц тела при деформации.
Вопрос 4. Какую природу имеет сила упругости?
Ответ. Сила упругости, как и сила трения – электромагнитная сила. Она возникает вследствие взаимодействия между частицами деформируемого тела.
Вопрос 5. От чего зависит коэффициент жесткости k? Модуль Юнга E?
Ответ. Коэффициент жесткости зависит от материала тела, а также его формы и размеров. Модуль Юнга зависит только от свойств материала тела.
Задачи на силу упругости и закон Гука с решениями
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Задача №1. Расчет силы упругости
Условие
Один конец проволоки жестко закреплен. С какой силой нужно тянуть за второй конец, чтобы растянуть проволоку на 5 мм? Жесткость проволоки известна и равна 2*10^6 Н/м2.
Решение
Запишем закон Гука:
По третьему закону Ньютона:
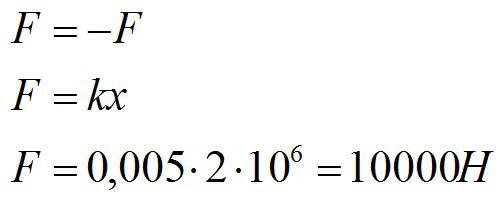
Ответ: 10 кН.
Задача №2. Нахождение жесткости пружины
Условие
Пружину, жесткость которой 100 Н/м, разрезали на две части. Чему равна жесткость каждой пружины?
Решение
По определению, жесткость обратно-пропорциональна длине. При одинаковой силе F неразрезанная пружина растянется на х, а разрезанная – на x1=x/2.
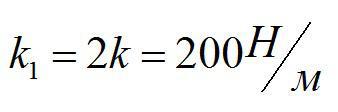
Ответ: 200 Н/м
При растяжении пружины в ее витках возникают сложные деформации кручения и изгиба, однако мы не учитываем их при решении задач.
Задача №3. Нахождение ускорения тела
Условие
Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины, которая при движении растянулась на 2 см. Жесткость пружины 200 Н/м. Определить ускорение, с которым движется тело.
Решение
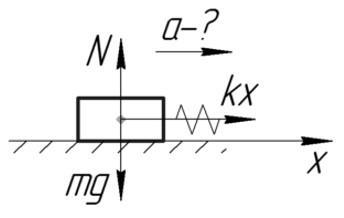
За силу, которая приложена к телу и заставляет его двигаться, можно принять силу упругости. По второму закону Ньютона и по закону Гука:
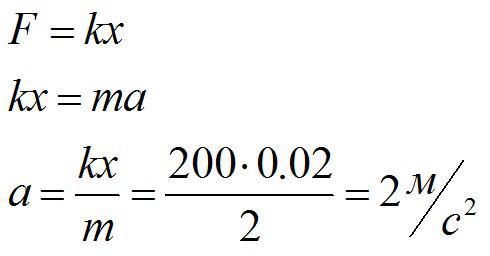
Ответ: 2 м/с^2.
Задача №4. Нахождение жесткости пружины по графику
Условие
На графике изображена зависимость модуля силы упругости от удлинения пружины. Найти жесткость пружины.
Решение
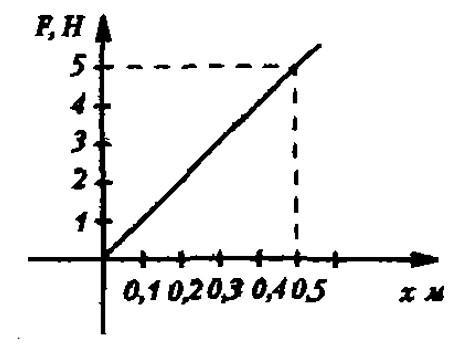
Вспоминаем, что жесткость равна отношению силы и удлинения. Представленная зависимость – линейная. В любой точке прямой отношение ординаты F и абсциссы х дает результат 10 Н/м.
Ответ: k=10 Н/м.
Задача №5. Определение энергии деформации
Условие
Для сжатия пружины на х1=2 см надо приложить силу 10 Н. Определить энергию упругой деформации пружины при сжатии на х2=4 см из недеформированного состояния.
Решение
Энергия сжатой пружины равна:
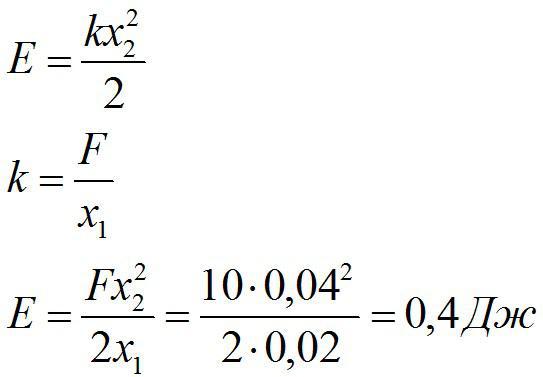
Ответ: 0,4 Дж.
Нужна помощь в решении задач? Обращайтесь за ней в профессиональный студенческий сервис.
Источник
Рано или поздно при изучении курса физики ученики и студенты сталкиваются с задачами на силу упругости и закон Гука, в которых фигурирует коэффициент жесткости пружины. Что же это за величина, и как она связана с деформацией тел и законом Гука?
Сила упругости и закон Гука
Для начала определим основные термины, которые будут использоваться в данной статье. Известно, если воздействовать на тело извне, оно либо приобретет ускорение, либо деформируется. Деформация — это изменение размеров или формы тела под влиянием внешних сил. Если объект полностью восстанавливается после прекращения нагрузки, то такая деформация считается упругой; если же тело остается в измененном состоянии (например, согнутом, растянутом, сжатым и т. д. ), то деформация пластическая.
Примерами пластических деформаций являются:
- лепка из глины;
- погнутая алюминиевая ложка.
В свою очередь, упругими деформациями будут считаться:
- резинка (можно растянуть ее, после чего она вернется в исходное состояние);
- пружина (после сжатия снова распрямляется).
В результате упругой деформации тела (в частности, пружины) в нем возникает сила упругости, равная по модулю приложенной силе, но направленная в противоположную сторону. Сила упругости для пружины будет пропорциональна ее удлинению. Математически это можно записать таким образом:
F = — k·x;
где F — сила упругости, x — расстояние, на которое изменилась длина тела в результате растяжения, k — необходимый для нас коэффициент жесткости. Указанная выше формула также является частным случаем закона Гука для тонкого растяжимого стержня. В общей форме этот закон формулируется так: «Деформация, возникшая в упругом теле, будет пропорциональна силе, которая приложена к данному телу». Он справедлив только в тех случаях, когда речь идет о малых деформациях (растяжение или сжатие намного меньше длины исходного тела).
Определение коэффициента жесткости
Коэффициент жесткости (он также имеет названия коэффициента упругости или пропорциональности) чаще всего записывается буквой k, но иногда можно встретить обозначение D или c. Численно жесткость будет равна величине силы, которая растягивает пружину на единицу длины (в случае СИ — на 1 метр). Формула для нахождения коэффициента упругости выводится из частного случая закона Гука:
k = F/x.
Чем больше величина жесткости, тем больше будет сопротивление тела к его деформации. Также коэффициент Гука показывает, насколько устойчиво тело к действию внешней нагрузки. Зависит этот параметр от геометрических параметров (диаметра проволоки, числа витков и диаметра намотки от оси проволоки) и от материала, из которого она изготовлена.
Единица измерения жесткости в СИ — Н/м.
Расчет жесткости системы
Встречаются более сложные задачи, в которых необходим расчет общей жесткости. В таких заданиях пружины соединены последовательно или параллельно.
Последовательное соединение системы пружин
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
1/k = 1/k1 + 1/k2 + … + 1/ki,
где k — общая жесткость системы, k1, k2, …, ki — отдельные жесткости каждого элемента, i — общее количество всех пружин, задействованных в системе.
Параллельное соединение системы пружин
В случае когда пружины соединены параллельно, величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
k = k1 + k2 + … + ki.
Измерение жесткости пружины опытным путем — в этом видео.
Вычисление коэффициента жесткости опытным методом
С помощью несложного опыта можно самостоятельно рассчитать, чему будет равен коэффициент Гука. Для проведения эксперимента понадобятся:
- линейка;
- пружина;
- груз с известной массой.
Последовательность действий для опыта такова:
- Необходимо закрепить пружину вертикально, подвесив ее к любой удобной опоре. Нижний край должен остаться свободным.
- При помощи линейки измеряется ее длина и записывается как величина x1.
- На свободный конец нужно подвесить груз с известной массой m.
- Длина пружины измеряется в нагруженном состоянии. Обозначается величиной x2.
- Подсчитывается абсолютное удлинение: x = x2-x1. Для того чтобы получить результат в международной системе единиц, лучше сразу перевести его из сантиметров или миллиметров в метры.
- Сила, которая вызвала деформацию, — это сила тяжести тела. Формула для ее расчета — F = mg, где m — это масса используемого в эксперименте груза (переводится в кг), а g — величина свободного ускорения, равная приблизительно 9,8.
- После проведенных расчетов остается найти только сам коэффициент жесткости, формула которого была указана выше: k = F/x.
Примеры задач на нахождение жесткости
Задача 1
На пружину длиной 10 см действует сила F = 100 Н. Длина растянутой пружины составила 14 см. Найти коэффициент жесткости.
- Рассчитываем длину абсолютного удлинения: x = 14—10 = 4 см = 0,04 м.
- По формуле находим коэффициент жесткости: k = F/x = 100 / 0,04 = 2500 Н/м.
Ответ: жесткость пружины составит 2500 Н/м.
Задача 2
Груз массой 10 кг при подвешивании на пружину растянул ее на 4 см. Рассчитать, на какую длину растянет ее другой груз массой 25 кг.
- Найдем силу тяжести, деформирующей пружину: F = mg = 10 · 9.8 = 98 Н.
- Определим коэффициент упругости: k = F/x = 98 / 0.04 = 2450 Н/м.
- Рассчитаем, с какой силой действует второй груз: F = mg = 25 · 9.8 = 245 Н.
- По закону Гука запишем формулу для абсолютного удлинения: x = F/k.
- Для второго случая подсчитаем длину растяжения: x = 245 / 2450 = 0,1 м.
Ответ: во втором случае пружина растянется на 10 см.
Видео
Из этого видео вы узнаете, как определить жесткость пружины.
Источник
