Перемещения при растяжении сжатии с учетом собственного веса
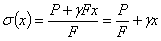
Подбор сечений с учетом собственного веса (при растяжении и сжатии).
При установлении внешних сил, растягивающих или сжимающих элементы конструкций, мы до сих пор игнорировали собственный вес этих элементов. Возникает вопрос, не вносится ли этим упрощением расчета слишком большая погрешность? В связи с этим подсчитаем величины напряжений и деформаций при учете влияния собственного веса растянутых или сжатых стержней.
Пусть вертикальный стержень (Рис.1, а) закреплен своим верхним концом; к нижнему его концу подвешен груз Р. Длина стержня l, площадь поперечного сечения F, удельный вес материала и модуль упругости Е. Подсчитаем напряжения по сечению АВ, расположенному на расстоянии от свободного конца стержня.
а) б)
Рис.1. Исходная расчетная схема бруса а) и б) равновесие нижней отсеченной части.
Рассечем стержень сечением АВ и выделим нижнюю часть длиной с приложенными к ней внешними силами (Рис.1, б) грузом Р и ее собственным весом . Эти две силы уравновешиваются напряжениями, действующими на площадь АВ от отброшенной части. Эти напряжения будут нормальными, равномерно распределенными по сечению и направленными наружу от рассматриваемой части стержня, т. е. растягивающими. Величина их будет равна:
Таким образом, при учете собственного веса нормальные напряжения оказываются неодинаковыми во всех сечениях. Наиболее напряженным, опасным, будет верхнее сечение, для которого достигает наибольшего значения l; напряжение в нем равно:
Условие прочности должно быть выполнено именно для этого сечения:
Отсюда необходимая площадь стержня равна:
От формулы, определяющей площадь растянутого стержня без учета влияния собственного веса, эта формула отличается лишь тем, что из допускаемого напряжения вычитается величина .
Чтобы оценить значение этой поправки, подсчитаем ее для двух случаев. Возьмем стержень из мягкой стали длиной 10 м; для него , а величина . Таким образом, для стержня из мягкой стали поправка составит т. е. около 0,6%. Теперь возьмем кирпичный столб высотой тоже 10 м; для него , а величина Таким образом, для кирпичного столба поправка составит , т.е. уже 15%.
Вполне понятно, что влиянием собственного веса при растяжении и сжатии стержней можно пренебрегать, если мы не имеем дела с длинными стержнями или со стержнями из материала, обладающего сравнительно небольшой прочностью (камень, кирпич) при достаточном весе. При расчете длинных канатов подъемников, различного рода длинных штанг и высоких каменных сооружений (башни маяков, опоры мостовых ферм) приходится вводить в расчет и собственный вес конструкции.
В таких случаях возникает вопрос о целесообразной форме стержня. Если мы подберем сечение стержня так, что дадим одну и ту же площадь поперечного сечения по всей длине, то материал стержня будет плохо использован; нормальное напряжение в нем дойдет до допускаемого лишь в одном верхнем сечении; во всех прочих сечениях мы будем иметь запас в напряжениях, т. е. излишний материал. Поэтому желательно так запроектировать размеры стержня, чтобы во всех его поперечных сечениях (перпендикулярных к оси) нормальные напряжения были постоянны,
Такой стержень называется стержнем равного сопротивления растяжению или сжатию. Если при этом напряжения равны допускаемым, то такой стержень будет иметь наименьший вес.
Возьмем длинный стержень, подверженный сжатию силой Р и собственным весом (Рис.2). Чем ближе к основанию стержня мы будем брать сечение, тем больше будет сила, вызывающая напряжения в этом сечении, тем большими придется брать размеры площади сечения. Стержень получит форму, расширяющуюся книзу. Площадь сечения F будет изменяться по высоте в зависимости от , т. е. .
Установим этот закон изменения площади в зависимости от расстояния сечения от верха стержня.
Рис.2. Расчетная схема бруса равного сопротивления
Площадь верхнего сечения стержня определится из условия прочности:
и
где допускаемое напряжение на сжатие; напряжения во всех прочих сечениях стержня также должны равняться величине
Чтобы выяснить закон изменения площадей по высоте стержня, возьмем два смежных бесконечно близких сечения на расстоянии от верха стержня; расстояние между сечениями ; площадь верхнего назовем , площадь же смежного .
Приращение площади при переходе от одного сечения к другому должно воспринять вес элемента стержня между сечениями. Так как на площади он должен вызвать напряжение, равное допускаемому , то определится из условия:
Отсюда:
После интегрирования получаем:
При площадь ; подставляя эти значения, имеем:
и
Отсюда
,
Если менять сечения точно по этому закону, то боковые грани стержня получат криволинейное очертание (Рис.2), что усложняет и удорожает работу. Поэтому обычно такому сооружению придают лишь приближенную форму стержня равного сопротивления, например в виде усеченной пирамиды с плоскими гранями. Приведенный расчет является приближенным. Мы предполагали, что по всему сечению стержня равного сопротивления передаются только нормальные напряжения; на самом деле у краев сечения напряжения будут направлены по касательной к боковой поверхности.
В случае длинных канатов или растянутых штанг форму стержня равного сопротивления осуществляют тоже приближенно, разделяя стержень по длине на ряд участков; на протяжении каждого участка сечение остается постоянным (Рис.3) получается так называемый ступенчатый стержень.
Рис.3. Эквивалентный ступенчатый брус с приближением к модели бруса равного сопротивления
Определение площадей … при выбранных длинах производится следующим образом. Площадь поперечного сечения первого нижнего участка будет по формуле равна:
Чтобы получить площадь поперечного сечения второго участка, надо нагрузить его внешней силой Р и весом первого участка:
Для третьего участка к внешней силе добавляются веса первого и второго участков. Подобным же образом поступают и для других участков.
Деформации при действии собственного веса.
При определении влияния собственного веса на деформацию при растяжении и сжатии стержней придется учесть, что относительное удлинение различных участков стержня будет переменным, как и напряжение . Для вычисления полного удлинения стержня постоянного сечения определим сначала удлинение бесконечно малого участка стержня длиной , находящегося на расстоянии от конца стержня (Рис.4).
Рис.4. Расчетная модель бруса с учетом собственного веса.
Абсолютное удлинение этого участка равно
Полное удлинение стержня равно:
Величина представляет собой полный вес стержня. Таким образом, для вычисления удлинения от действия груза и собственного веса можно воспользоваться прежней формулой:
подразумевая под S внешнюю силу и половину собственного веса стержня.
Что же касается деформаций стержней равного сопротивления, то, так как нормальные напряжения во всех сечениях одинаковы и равны допускаемым , относительное удлинение по всей длине стержня одинаково и равно
Абсолютное же удлинение при длине стержня l равно:
где обозначения соответствуют приведенным на рис.1.
Деформацию ступенчатых стержней следует определять по частям, выполняя подсчеты по отдельным призматическим участкам. При определении деформации каждого участка учитывается не только его собственный вес, но и вес тех участков, которые влияют на его деформацию, добавляясь к внешней силе. Полная деформация получится суммированием деформаций отдельных участков.
Дальше…
Источник
Подбор
сечений с учетом собственного веса (при
растяжении и сжатии).
При установлении
внешних сил, растягивающих или сжимающих
элементы конструкций, мы до сих пор
игнорировали собственный вес этих
элементов. Возникает вопрос, не вносится
ли этим упрощением расчета слишком
большая погрешность? В связи с этим
подсчитаем величины напряжений и
деформаций при учете влияния собственного
веса растянутых или сжатых стержней.
Пусть вертикальный
стержень (Рис.1, а) закреплен своим
верхним концом; к нижнему его концу
подвешен грузР. Длина стержняl,
площадь поперечного сеченияF,
удельный вес материала![]() и
и
модуль упругостиЕ. Подсчитаем
напряжения по сечениюАВ, расположенному
на расстоянии![]() от
от
свободного конца стержня.
а) б)
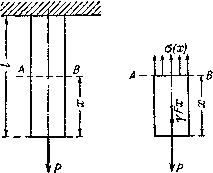
Рис.1 Исходная расчетная схема бруса а)
и б) — равновесие нижней отсеченной
части.
Рассечем стержень
сечением АВи выделим нижнюю часть
длиной![]() с
с
приложенными к ней внешними силами
(Рис.1, б) — грузомРи ее собственным
весом![]() .
.
Эти две силы уравновешиваются напряжениями,
действующими на площадьАВ от
отброшенной части. Эти напряжения будут
нормальными, равномерно распределенными
по сечению и направленными наружу от
рассматриваемой части стержня, т. е.
растягивающими. Величина их будет равна:
![]()
Таким образом, при
учете собственного веса нормальные
напряжения оказываются неодинаковыми
во всех сечениях. Наиболее напряженным,
опасным, будет верхнее сечение, для
которого![]() достигает
достигает
наибольшего значенияl; напряжение
в нем равно:
![]()
Условие прочности
должно быть выполнено именно для этого
сечения:
![]()
Отсюда необходимая
площадь стержня равна:
![]()
От формулы,
определяющей площадь растянутого
стержня без учета влияния собственного
веса, эта формула отличается лишь тем,
что из допускаемого напряжения вычитается
величина
![]() .
.
Чтобы оценить
значение этой поправки, подсчитаем ее
для двух случаев. Возьмем стержень из
мягкой стали длиной 10 м; для него
![]() ,
,
а величина![]() .
.
Таким образом, для стержня из мягкой
стали поправка составит![]() т.
т.
е. около 0,6%. Теперь возьмем кирпичный
столб высотой тоже 10м; для него![]() ,
,
а величина![]() Таким
Таким
образом, для кирпичного столба поправка
составит![]() ,
,
т.е. уже 15%.
Вполне понятно,
что влиянием собственного веса при
растяжении и сжатии стержней можно
пренебрегать, если мы не имеем дела с
длинными стержнями или со стержнями из
материала, обладающего сравнительно
небольшой прочностью (камень, кирпич)
при достаточном весе. При расчете длинных
канатов подъемников, различного рода
длинных штанг и высоких каменных
сооружений (башни маяков, опоры мостовых
ферм) приходится вводить в расчет и
собственный вес конструкции.
В таких случаях
возникает вопрос о целесообразной форме
стержня. Если мы подберем сечение стержня
так, что дадим одну и ту же площадь
поперечного сечения по всей длине, то
материал стержня будет плохо использован;
нормальное напряжение в нем дойдет до
допускаемого лишь в одном верхнем
сечении; во всех прочих сечениях мы
будем иметь запасв напряжениях, т.
е. излишний материал. Поэтому желательно
так запроектировать размеры стержня,чтобы во всех его поперечных сечениях
(перпендикулярных к оси) нормальные
напряжения были постоянны,
Такой стержень
называется стержнем равного сопротивлениярастяжению или сжатию. Если при этом
напряжения равны допускаемым, то такой
стержень будет иметь наименьший вес.
Возьмем длинный
стержень, подверженный сжатию силой Ри собственным весом (Рис.2). Чем ближе к
основанию стержня мы будем брать сечение,
тем больше будет сила, вызывающая
напряжения в этом сечении, тем большими
придется брать размеры площади сечения.
Стержень получит форму, расширяющуюся
книзу. Площадь сеченияFбудет
изменяться по высоте в зависимости от![]() ,
,
т. е.![]() .
.
Установим этот
закон изменения площади в зависимости
от расстояния сечения
![]() от
от
верха стержня.
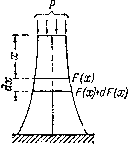
Рис. 2 Расчетная схема бруса равного
сопротивления
Площадь верхнего
сечения стержня
![]() определится
определится
из условия прочности:
![]() и
и![]()
где
![]() —
—
допускаемое напряжение на сжатие;
напряжения во всех прочих сечениях
стержня также должны равняться величине
![]()
Чтобы выяснить
закон изменения площадей по высоте
стержня, возьмем два смежных бесконечно
близких сечения на расстоянии
![]() от
от
верха стержня; расстояние между сечениями![]() ;
;
площадь верхнего назовем![]() ,
,
площадь же смежного![]() .
.
Приращение площади
![]() при
при
переходе от одного сечения к другому
должно воспринять вес![]() элемента
элемента
стержня между сечениями. Так как на
площади![]() он
он
должен вызвать напряжение, равное
допускаемому![]() ,
,
то![]() определится
определится
из условия:
![]()
Отсюда:
![]()
После интегрирования
получаем:
![]()
При
![]() площадь
площадь![]() ;
;
подставляя эти значения, имеем:
![]() и
и![]()
Отсюда
![]() ,
,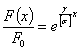
![]()
Если менять сечения
точно по этому закону, то боковые грани
стержня получат криволинейное очертание
(Рис.2), что усложняет и удорожает работу.
Поэтому обычно такому сооружению придают
лишь приближенную форму стержня равного
сопротивления, например в виде усеченной
пирамиды с плоскими гранями. Приведенный
расчет является приближенным. Мы
предполагали, что по всему сечению
стержня равного сопротивления передаются
только нормальные напряжения; на самом
деле у краев сечения напряжения будут
направлены по касательной к боковой
поверхности.
В случае длинных
канатов или растянутых штанг форму
стержня равного сопротивления осуществляют
тоже приближенно, разделяя стержень по
длине на ряд участков; на протяжении
каждого участка сечение остается
постоянным (Рис.3) — получается так
называемый ступенчатый стержень.
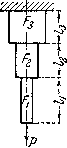
Рис.3 Эквивалентный ступенчатый брус с
приближением к модели бруса равного
сопротивления
Определение
площадей
![]() …
…
при выбранных длинах производится
следующим образом. Площадь поперечного
сечения первого нижнего участка будет
по формуле равна:
![]()
Чтобы получить
площадь поперечного сечения второго
участка, надо нагрузить его внешней
силой Ри весом первого участка![]() :
:
![]()
Для третьего
участка к внешней силе добавляются веса
первого и второго участков. Подобным
же образом поступают и для других
участков.
Деформации
при действии собственного веса.
При определении
влияния собственного веса на деформацию
при растяжении и сжатии стержней придется
учесть, что относительное удлинение
различных участков стержня будет
переменным, как и напряжение
![]() .
.
Для вычисления полного удлинения стержня
постоянного сечения определим сначала
удлинение бесконечно малого участка
стержня длиной![]() ,
,
находящегося на расстоянии![]() от
от
конца стержня (Рис.4).
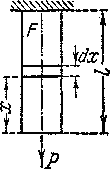
Рис.4 Расчетная модель бруса с учетом
собственного веса.
Абсолютное удлинение
этого участка равно
![]()
Полное удлинение
стержня
![]() равно:
равно:
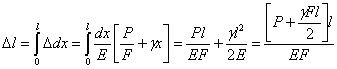
Величина
![]() представляет
представляет
собой полный вес стержня. Таким образом,
для вычисления удлинения от действия
груза и собственного веса можно
воспользоваться прежней формулой:
![]()
подразумевая под
Sвнешнюю силу и половину собственного
веса стержня.
Что же касается
деформаций стержней равного сопротивления,
то, так как нормальные напряжения во
всех сечениях одинаковы и равны
допускаемым
![]() ,
,
относительное удлинение по всей длине
стержня одинаково и равно
![]()
Абсолютное же
удлинение при длине стержня lравно:
![]()
где обозначения
соответствуют приведенным на рис.1.
Деформацию
ступенчатых стержней следует определять
по частям, выполняя подсчеты по отдельным
призматическим участкам. При определении
деформации каждого участка учитывается
не только его собственный вес, но и вес
тех участков, которые влияют на его
деформацию, добавляясь к внешней силе.
Полная деформация получится суммированием
деформаций отдельных участков.
Источник
Напряжение в призматическом брусе
Собственный вес при расчетах на растяжение-сжатие учитывается для конструкций, вес которых сопоставима со значениями внешних нагрузок. Это могут быть железобетонные колонны, кирпичные простенки и др.
Рассмотрим внутренние усилия и напряжения, возникающие в растянутом стержне при одновременном действии сосредоточенной силы $F$ и собственного веса. Вес стержня определяется как
$Q = gamma cdot V = gamma cdot A cdot l$,
где $gamma $ – удельный вес материала [кН/м3], $V$, $A$, $l$ – об’объем, площадь сечения и длина стержня соответственно. Удельный вес эт’связана с плотностью материала $gamma = g cdot rho $, где $g approx 10$ м/с2, $rho $– плотность.
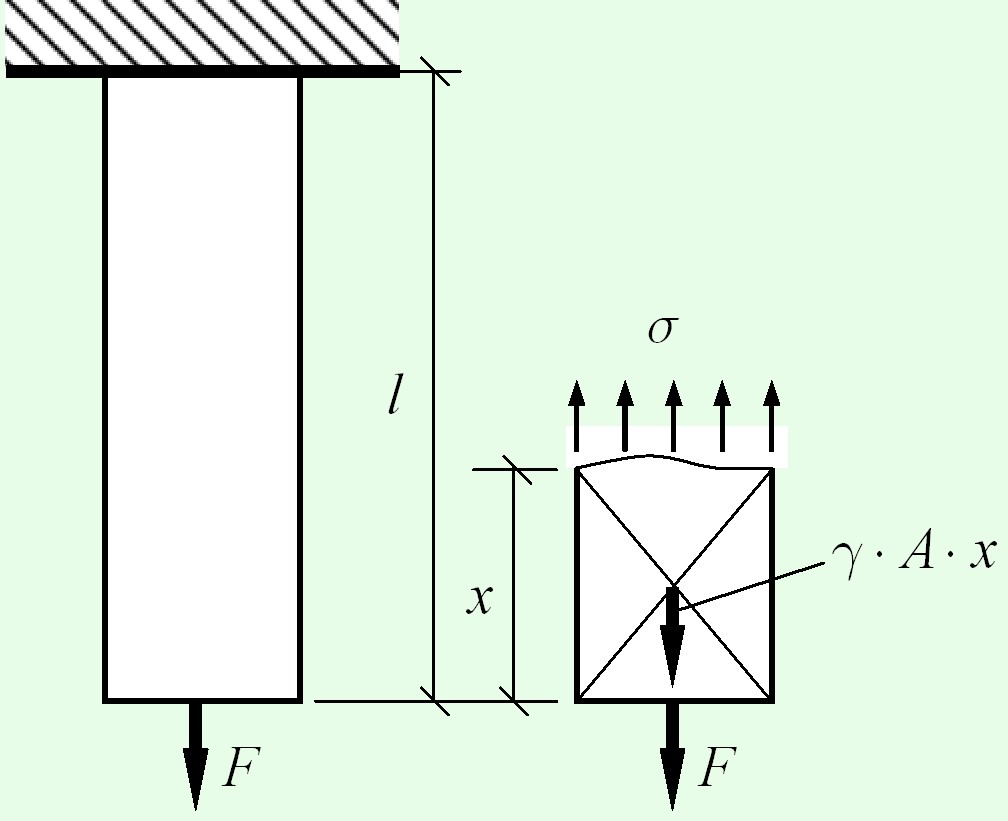
Продольная сила, возникающая в сечении И – И
$N = F + gamma cdot A cdot x$
Напряжение при учете собственного веса
$sigma = frac{N}{A} = frac{F}{A} + gamma cdot x$
Наибольшее напряжение возникает в верхнем сечении и условие прочности примет вид
${sigma _{max }} = frac{F}{A} + gamma cdot l leqslant left[ sigma right]$
Подбор площади сечения с учетом собственного веса
${A_{min }} = frac{F}{{left[ sigma right] — gamma cdot l}}$
Брус равного сопротивления
Брусом равного сопротивления называется брус, в котором напряжения по длине не меняются и, как правило, равны допустимым напряжением.
Вполне понятно, чтобы удовлетворить таким условиям, площадь сечения бруса должна меняться в соответствии с изменением продольной силы. Рассмотрим бесконечно малый элемент бруса (рис.) длиной $dx$. Нижний сечение этого элемента имеет площадь $A$. Продольная сила в нем равна $[sigma ] cdot A$. Продольная сила в верхнем сечении увеличивается на величину веса элемента, то есть на $dN = gamma cdot dV = gamma cdot A cdot dx$. Соответственно площадь увеличивается на величину $dA = frac{{dN}}{{[sigma ]}}$.
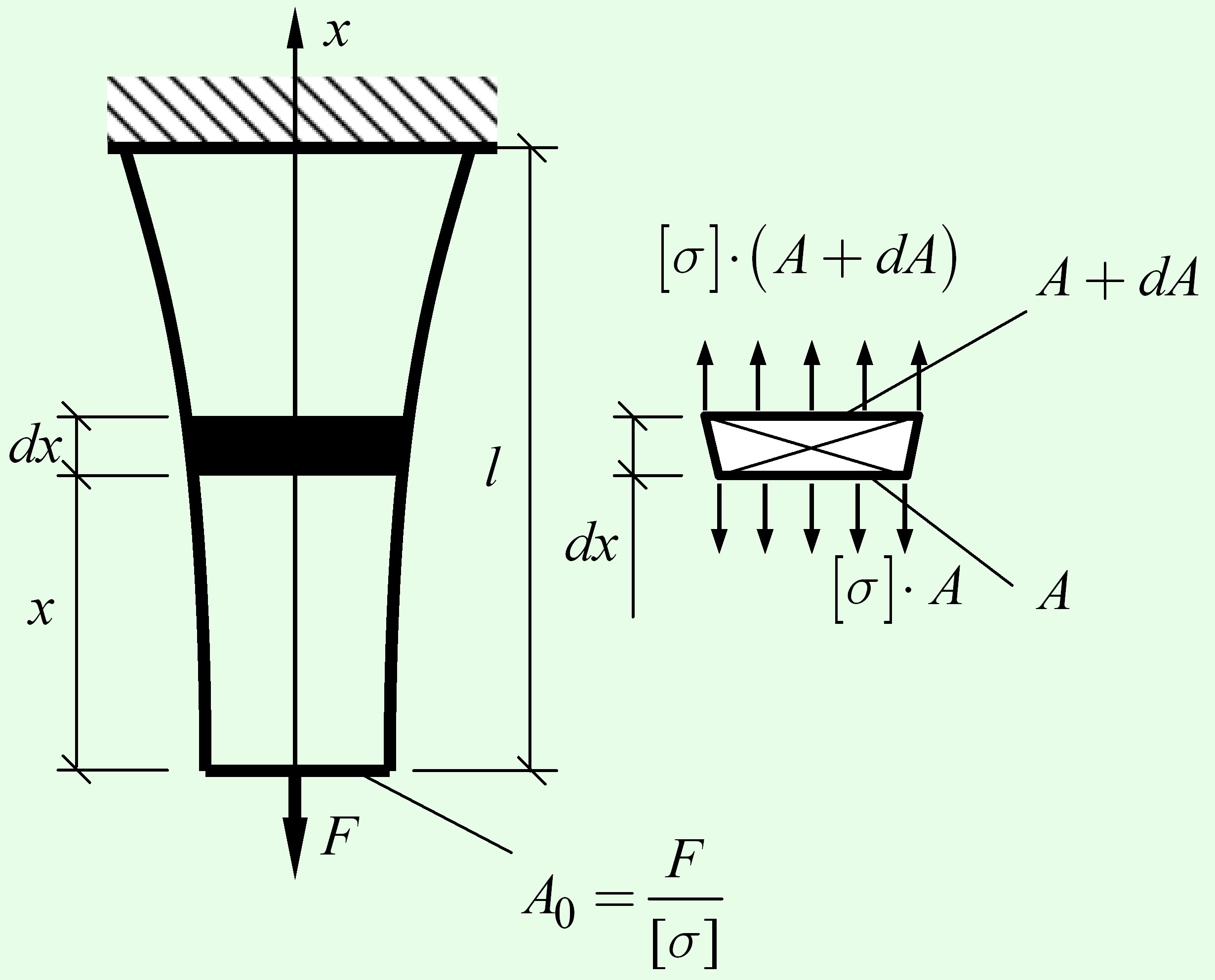
Таким образом,
$dN = gamma cdot A cdot dx = dA cdot [sigma ]$,
$frac{{dA}}{A} = frac{gamma }{{left[ sigma right]}} cdot dx$, [int {frac{{dA}}{A}} = int {frac{gamma }{{left[ sigma right]}} cdot dx} ], $ln left( A right) = frac{gamma }{{left[ sigma right]}} cdot x + C$.
В нижнем сечении, где продольная сила $N = F$, площадь сечения должна быть
${A_0} = frac{F}{{[sigma ]}}$.
Тогда
$ln left( {{A_0}} right) = frac{gamma }{{left[ sigma right]}} cdot 0 + C,,,, Rightarrow ,,,,,C = ln left( {{A_0}} right)$,
$ln left( A right) — ln left( {{A_0}} right) = frac{gamma }{{left[ sigma right]}} cdot x$,
$frac{A}{{{A_0}}} = {e^{frac{gamma }{{left[ sigma right]}} cdot x}}$.
то Есть, для обеспечения одинаковых напряжений по длине стержня, площадь сечения должна изменяться по экспоненциальной зависимостью
$A(x) = {A_0} cdot e{,^{frac{gamma }{{left[ sigma right]}} cdot x}}$.
Ступенчатый брус
Брус равного сопротивления неудобен для изготовления, поэтому для выравнивания напряжений используют ступенчатое изменение сечения по длине. При этом количество и длину ступеней определяют в зависимости от ситуации, а необходимую площадь сечения каждой ступени назначают из условия прочности как для призматического бруса. Например, для трехступенчатого бруса с нагрузкой на его конце расчет площадей сечения проводится, как показано на рис.6.3.

Деформации от собственного веса
Напряжение при учете только собственного веса для призматического бруса
$sigma = frac{{gamma cdot A cdot x}}{A} = gamma cdot x$.
По закону Гука
[varepsilon = frac{sigma }{E} = frac{{gamma x}}{E}]
[Delta l = intlimits_0^l {dDelta l} = intlimits_0^l {frac{gamma }{E} cdot dx} = frac{gamma }{E} cdot left. {frac{{{x^2}}}{2}} right|_0^l = frac{gamma }{E} cdot frac{{{l^2}}}{2} = frac{{Q cdot l}}{{2 cdot EA}}].
Если на стержень, кроме собственного веса $Q$ действует сила $F$, удлинение будет определяться по формуле
$Delta l = frac{{N,l}}{{EA}} + frac{{Q,l}}{{2,EA}}$.
Деформации бруса равного сопротивления определяются проще, потому что напряжение во всех сечениях одинаковы $sigma = left[ sigma right] = const$, тогда по закону Гука
$varepsilon = frac{{left[ sigma right]}}{E} = const$,
$Delta l = varepsilon cdot l = frac{{left[ sigma right]}}{E} cdot l$
Источник
